大规模数据集谱聚类并行优化算法

郝笑弘，尹青山

（1.山西水利职业技术学院，山西 太原030032；2.吉林大学软件学院，吉林 长春130012）

1 引言

计算机技术的快速发展和网络带宽的不断扩展，海量多样化数据成为当前数据处理的常态，面对海量数据，如何挖掘出最有价值信息成为研究的热点，聚类作为数据挖掘的重要手段和研究方向，通过广泛的探索性分析和数据内在联系识别，达到相似特征数据的归类，从而提示数据的隐藏价值［1］。谱聚类以非线性核距离作为聚类相似判断依据，适用于非凸等任意形状的数据，且能够取得全局最优解［2］。但传统谱聚类计算代价与存储开销阻碍了其在大规模数据集中的应用，且数据规模越大，这种性能瓶颈越明显。

为此，文献［3］兼顾视角内划分质量与视角间协同，通过多代表点策略和多视角代表性保持对多样化大规模数据集进行一致性约束，并通过加权系数最大化与拉格朗日乘子实现数据的谱聚类，相比于传统谱聚类，改进算法在聚类时间和存储优化上具有一定的优势；文献［4］选用非负矩阵分解对多视角数据进行处理，以获得各视角的潜在特征矩阵，然后引入正交约束以优化局部特征，通过数据加权调整缺失数据的聚类贡献影响，最后通过分块处理以缓解大规模数据的内存需求；文献［5］以Nyström近似采样降低大规模数据的相似度计算复杂度，有利于聚类效率的提高，通过对采样过程的自适应优化要，进一步提高谱聚类在大规模数据集上的聚类效果；文献［6］将样本映射至高维函数核空间，通过领域信息建立系统加权滤波器和二维直方图，以此获得核空间的快速迭代，算法对大规模数据和高斯噪声具有较好的适应性和鲁棒性；

并行框架的广泛应用为谱聚类在大规模集上的使用提供了新的思路，文献［7］通过自适应格网划分与加权以及信息熵提高密度聚类的准确性，然后结合MapReduce框架对改进后的密度聚类时行局部簇并行优化，从而加快局部簇的生成与合并，有效提高算法的处理速率；文献［8］基于MapReduce的并行计算框架通过分片局部簇计算和全局簇增量合并对DBSCAN算法进行并行优化，以提高DBSCAN算法对大规模数据集的适用性，但算法的数据分块效率不高，且局部簇合并较为复杂；文献［9］改进Spark框架中占用内存较大的top操作，并通过自底向上的聚类策略提高层次聚类算法的区域性，提出基于Spark框架的并行图过滤聚类，其聚类效果优于其他相关并行策略；文献［10］以Hadoop和Spark双并行框架对密度聚类进行降低计算复杂度优化，并给出在两种并行框架下的数据分块策略，但算法的簇合并法效率不高［11］。

为引，在已有研究基础上，提出基于并行框架和Nystrom采样相结合的改进谱聚类算法，算法在自适应相似矩阵计算基础上，通过数据分块和单向节点并行，提高算法相似矩阵的计算效率，通过Nystrom加权抽样逼近，减少拉普拉斯矩阵特征向量的计算复杂度，最后通过KD树结构进一步减少k-mean聚类过程的距离计算，从而降低了传统谱聚类的计算复杂度，提高了聚类效率，仿真实验验证了算法的有效性。

2 谱聚类并行优化

2.1 谱聚类算法流程

谱聚类算法采用无向图思想，将数据集中的数据视为无向图中的节点，而数据之间的相似度，则表示为节点间的权重，然后根据权重规则将无向图划分为不同的子图，通过子图内的边的高权重与子图间边的低权重优化实现数据的聚类分析。谱聚类最优划分求解通常依赖拉普拉斯矩阵，其流程为：

（1）输入初始类数k及相似矩阵S∈Rn×n，然后建立数据集的相似图，计算边的权重矩阵W；

（2）计算图的拉普拉斯矩阵L，并给出其前k个特征向量组成的矩阵对V的每一行时行规范化处理，使其范数值为1，得到矩阵U=[uij]，其中，

（3）设yi∈Rk对应矩阵U的i列，i=1,2,…,n，则通过k-means算法对yi∈Rk进行聚类，聚类结果为C1,C2,…,Ck。

2.2 自适应相似矩阵并行计算

在进行无向图划分时，需要先通过高斯核函数度量数据之间距离，进而形成数据的相似性连接图，相似图对应一个相似矩阵，通常数据挖掘需要处理多样化数据，因而相似图通常采用全连接图，这样由数据距离值计算无向图的边权值为：

式中：Aij-两数据xi和xj之间的连接边权值；σ-数据邻域范围控制的尺度参数，用以调整两数据之间的相异度；d(xi,xj)-两个数据xi和xj之间距离。

根据文献中self-Tunin聚类思想［11］可得到数据xi到xj的相异度xj到xi的相异度，则可以得到相似函数的参数自适应形式，即

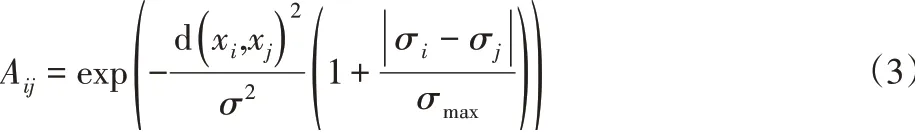
式中：σi-当前数据xi与其邻域的距离均值，用于描述当前数据的邻域密度，σ-σi均值数据密度差值，σmax-的最大值权值因子，用以调整高斯核函数。

对于大规模数据集，上述自适应相似矩阵的计算量巨大，为此基于并行框架，在数据分块基础上，将不同数据块分发到框架的并行计算节点上，并行计算各节点内数据的相似度，然后根据框架节点序号，依次计算两节点内数据之间的相似度值，为减少数据重复计算，当前序号下的节点内数据，仅与比其序号值大的节点内数据计算相似度值。

由相似矩阵A={Aij}可以构建正则化Laplacian矩阵L为：

式中：D={Di,j}-对角矩阵，其计算式为：

可以证明，对于Ai,j≥0，其L矩阵对称且显半正定，这说明，当其局部聚类与其他局部聚类中的样本不相关时，L矩阵中将存在非零块对角阵，此时L的前k个最小特征值对应的特征向量组成矩阵V，再对V进行k-means等聚类，即可得到最终的谱聚类。

L矩阵的并行化计算过程，可以通过L′=D-1/2×L和L′×D-1/2两个并行化过程实现，L′=D-1/2×L并行计算过程如图1所示，L′×D-1/2采用相似的并行计算过程。

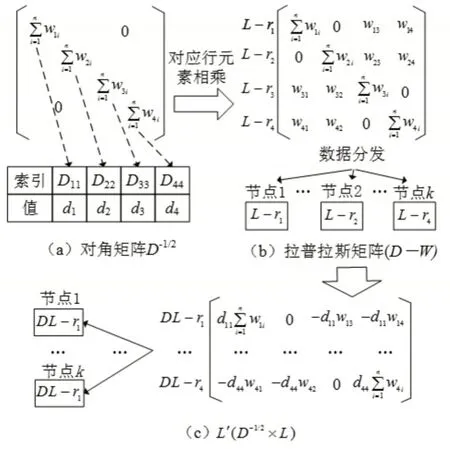
图1 矩阵L的并行化计算过程Fig.1 Parallel Computing Process of Matrix L

2.3 近似特征向量并行计算

针对大规模数据集，传统谱聚类采用的前k个特征向量组成的降维矩阵仍需要巨大的计算量，为此，采用Nyström采样方法进行特征向量的低秩逼近。

设数据集规模为n，随机抽样点数为m，则有( )n-m个数据为未抽样数据，则数据集的相似矩阵可表示为：

式中：A-抽样数据间的相似矩阵；B-抽样数据与其他数据间的相似矩阵；C-未被抽样的数据间的相似矩阵，由于式（6）中未被抽样数据的数据量远大于抽样数据，Nyström算法采用A和E来近似表示K：

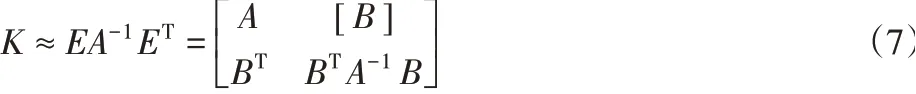
Nystrom采样方法通过矩阵的低秩逼近，仅需计算少量采样数据进行相关计算，避免了大规模数据集中未被采样数据的使用，从面极大程度降低算法的复杂度。但传统采样方法未充分考虑不同抽样数据的重要性，使得采样数据对最终结果的贡献度难以保证，为此采用加权采样形式，其加权核矩阵为：

设矩阵L的特征分解表示为L=ϕλϕT。式中：λ-特征值组成的对角阵，由A=ϕAλAϕAT可得：

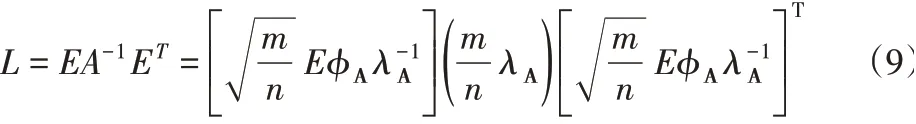
根据式（9）通过低秩逼近计算矩阵L的特征值及其对应的特征向量，即：

近似特征向量的计算流程，如图2所示。

图2 近似特征向量计算流程Fig.2 Similar Eigenvector Calculation Process

2.4 K-means并行计算

KD树通过查询当时节点最近邻的数据点进行距离比较，从而避免数据点之间的距离计算，实现快速节点匹配，为此，在谱聚类的k-means算法对特征向量进行聚类过程中，引入KD树作为特征矩阵的数据存储结构，并建立聚类中心KD结构，然后利用KD树自有的最近邻查询实现数据点与其距离最小的聚类中心点的归类，从而有效解决数据距离迭代计算的冗余，其过程如图3所示。

图3 基于KD树结构的快速k-means计算流程Fig.3 Fast K-means Calculation Process based on KD Tree Structure

3 算法性能实验验证

为验证文中算法在大规模数据集聚类方面的有效性，实验构建计算机集群，以进行并行分布式计算，选取UCI库中的Waveform集、Pendigits集和Forest集三个数据集作为实验数据集，并将数据集分别扩展为大规模数据集，以聚类准确率和标准化互信息作为聚类性能评价指标，实验中并行框架采用Spark V2.3.0，开源MPI V1.8。

3.1 算法聚类性能比较实验

为测试文中算法（简记为ImpSC，采样比例为10%）的聚类性能，实验选取原始谱聚类（简记为TrSC）、并行k-means算法（简记为Pkmeans）、随机抽样谱聚类（简记为RadSC）和特征自适应选择聚类算法（简记为AflC）作为实验比较算法，实验中在每个实验数据集上对进行20次实验，取实验结果的平均值，结果如表1所示。

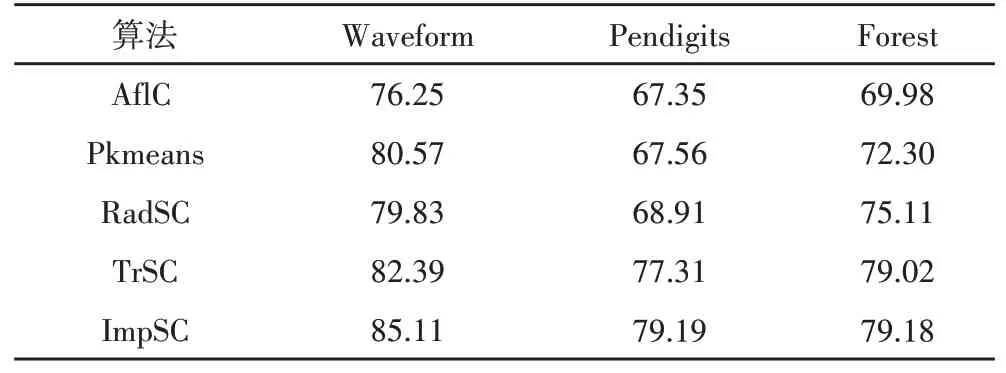
表1 各算法的聚类性能比较结果（%）Tab.1 Performance Comparison of each Algorithm（%）

从表1实验结果中可以看出，算法在各个大规模数据集上都取得较好的聚类准确率，其聚类结果与原始谱聚类相近，但略有优势，主要因为相似矩阵的参数自适应设置，使其更适于不同数据集的数据特征，从而验证了算法的聚类性能和相似矩阵自适应计算的有效性。

3.2 算法计算复杂性实验

加速比是检验改进算法的并行化能力的重要指标，为此，将Waveform集的数据规模人工扩充0.6G、1G、2G和3G，然后在不同节点下分析算法的加速比，实验结果如图4所示，图中实验结果为多次实验结果的平均值。从实验结果可以看出，当数据规模在0.6G时，由于数据规模较小，随着节点数增加，算法在处理数据分块和数据之间的通信方面占用资源较大，因而算法的加速比不高，甚至节点较多时，出现一定的下降，但随着数据规模增大，算法的加速比快速增大，主要因为数据规模越大，数据分块及节点通信占用的次源比重变小，而算法的并行运算优势凸显，从而验证改进算法更适于大规模数据集应用。

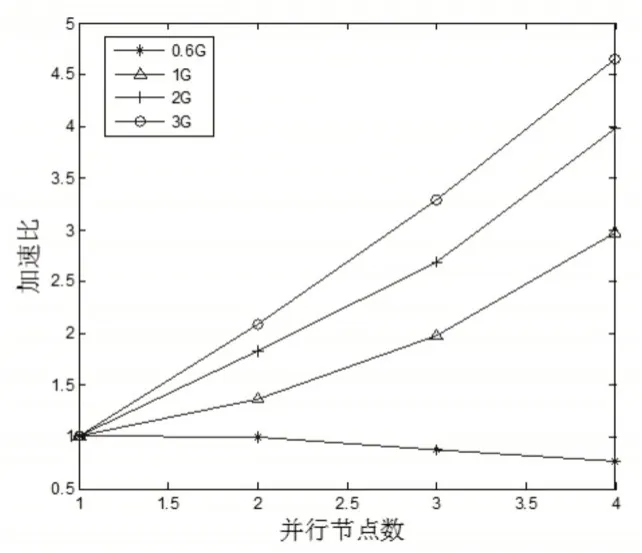
图4 不同节点数下的算法加速比Fig.4 Speedup Under Different Number of Nodes

4 总结

为解决传统谱聚类算法在应用于大规模数据上时，复杂度较高且资源占用较大，导致算法聚类效果不好甚至无法聚类的问题，提出基于并行框架和Nystrom采样相结合的改进谱聚类算法，算法在自适应相似矩阵计算基础上，通过数据分块和单向节点并行，提高算法相似矩阵的计算效率，通过Nystrom加权抽样逼近，减少拉普拉斯矩阵特征向量的计算复杂度，最后通过KD树结构进一步减少k-mean聚类过程的距离计算，从而降低传统谱聚类的计算复杂度，提高了聚类效率，仿真实验验证了算法的有效性。