电动行李箱车设计与研究

陈毅龙

（厦门大学创意与创新学院，福建 漳州363105）

1 引言

近年来，我国行李箱市场规模保持稳定增长，发展潜力巨大［1］，同时随着人们生活品质的提高，对行李箱品质和功能的需求也在不断增加，旅途中，当出现携带物品较重、行走距离较远、反复上下坡、行程较赶等情况时，传统的人力拖拉式行李箱会给出行造成诸多不便，为了解决这类痛点，需要设计一种可载人的电动行李箱车。当前，市场上出现个别行李箱车产品，这类产品存在或是只能站立不能乘坐，或是整备质量过大、容量偏小的问题。

车架作为主要承载结构，其强度和刚度不仅关系结构安全性和可靠性，也影响到用户体验，因此，在产品设计中，对车架强度和刚度的研究尤为重要。当前，有限元法已成为研究车架强度和刚度的重要手段［2-7］，在这些研究中，研究对象为市面上可见的各种车型车架，而对于新出现的行李箱车研究几乎空白。

鉴于此，进行了较为系统研究工作，研究内容如下：（1）设计了一款可乘坐、稳定可靠且方便携带的电动行李箱车；（2）制作实物模型，结合应变试验，建立正确的车架有限元模型；（3）研究车架在满载弯曲、弯扭联合、紧急制动和紧急转弯4种典型工况下的受力情况，同时进行模态分析。

2 电动行李箱车设计

2.1 设计任务

需求如下：能承载1个正常体重成年人，要求车架具有一定强度和刚度；旅途中的搬运、驾驶性能的需求、机场对行李尺寸重量的限制等情况都要求行李箱车结构紧凑、质量尽量小；民航对电池的携带规定限制了锂电池的规格，同时也要求锂电池可方便拆卸；能较舒适的坐在上面；操作方便，能快速实现收缩搬运和展开骑乘的功能切换；主要应用于机场内、机场酒店间、景区内、市区内等短途出行的场合，因行驶距离较短、路况较好，对动力性和续航能力要求不高。综合设计指标为：满载100kg以内；行李箱容积20寸；最大行驶速度20km/h以内；续航能力15km左右。

2.2 结构设计

整体结构，如图1所示。综合考虑强度、质量和成本，车架选用6系列以上的铝合金型材或板材焊接而成，车架包括行李箱框架、伸缩机构和转向架3部分，行李箱壳体与行李箱框架通过铆接固定，伸缩机构固定架固定于行李箱框架底部，伸缩机构移动架一端与转向杆通过轴承旋转配合，另一端与伸缩机构固定架小间隙配合，可在其中滑动，伸缩机构设有固定装置以确保电动行李箱车在展开或收缩后伸缩机构移动架不会滑动，只需将伸缩机构移动架拉出或推入伸缩机构固定架便可完成电动行李箱车的展开或收缩，操作简便，转向架兼具转向和拉杆的作用。动力方面，采用前轮轮毂电机驱动、前轮转向、前轮制动方式使结构紧凑，24V180W电机搭配4000mAH的锂电池确保所需的行驶和续航能力，锂电池置于伸缩机构移动架内，充分利用空间，可拆卸的设计加上小于100WH的规格使其可携带上飞机。行李箱框架顶部设计的座垫，伸缩机构移动架前端设计的脚踏可提高乘坐舒适性。

图1 电动行李车结构Fig.1 Motor-Driven Luggage Car Structure

3 车架有限元模型建立

有限元网格模型质量好坏直接影响分析结果的精准性［8］，为了获得较精准的网格模型，先对车架在弯曲工况下应力情况进行仿真并制作实物模型进行弯曲应力试验，将试验结果与仿真结果做比较分析以验证网格模型的精准性，为后续其他工况分析提供依据。

3.1 有限元理论

有限元法的基本思想是将问题的求解域化分为一系列单元，单元之间靠节点连接，用固体力学理论研究单元的性质，从建立单元位移模式入手，最终导出计算单元的刚度矩阵，其单元刚度矩阵公式可表述为：

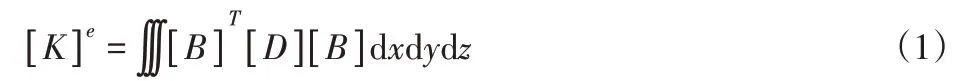
式中：[B]-单元刚度矩阵；[D]-与单元材料有关弹性矩阵。

利用最小势能原理，导出单元平衡方程为：

式中：{Fe}-单元等效节点力；{}δe-单元节点位移矩阵。

3.2 有限元软件仿真

对车架进行简化处理，忽略个别对承载力几乎没影响的结构，焊接处和固定连接处采用绑定接触方式模拟，伸缩架和车架之间采用摩擦接触，摩擦系数无穷大，处理后的车架有限元模型网格数为919362、节点数为260956、网格质量平均值大于0.86。

铝合金材料由于其突出的综合性能，特别是在轻量化上优秀表现，使其被越来越多的运用到车架设计上［9］，因此车架使用6061-T6铝镁合金材料制作。通过ANSYS Workbench模拟一个体重75kg的成年人坐在车架上的受力情况。体重80%（500N）施加在车架顶部3根方管处，体重20%（150N）施加在前方脚踏处，选取前、后轮架连接孔为约束处，约束前轮架支撑处X、Y、Z方向平动自由度，约束后轮架支撑处Y方向平动自由度，释放所有支点的转动自由度，载荷和约束条件如图2所示。

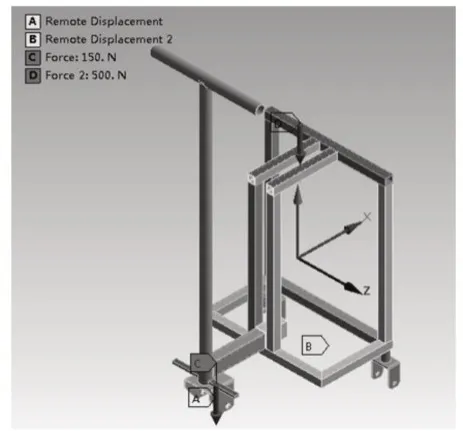
图2 载荷和约束条件Fig.2 Load and Constraint Conditions

求解该模型应力云图，求解后可知Z向应力值较大且接近等效应力，故选取Z向作为应变片贴片方向。Z向应力云图，如图3所示。图3（b）从底部往上仰视，展示最大应力。

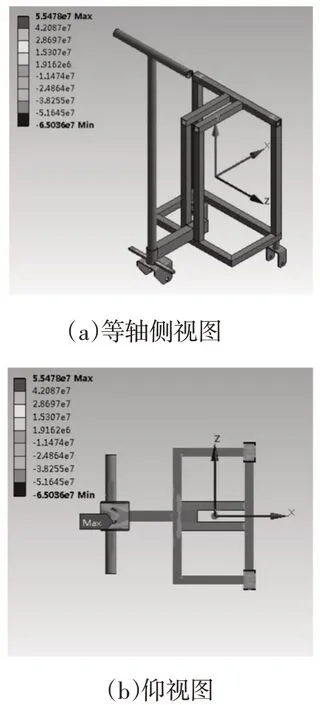
图3 试验模型Z向应力云图Fig.3 Z-Axis Stress Chart of Test Model

3.3 试验验证

如图3所示，最大应力值位于前轮转向杆和前轮架焊接处，其他较大应力区域在前轮架、后轮架、顶部横管和脚踏处，由于前轮转向杆和前轮架焊接处无法贴应变片，故选取其他较大应力区域进行试验，应变片布置情况如表1、图4所示。表1中片号对应图4中的序号。

表1 测点位置Tab.1 Location of Measuring Points

图4 应变片布置Fig.4 Strain Gauge Layout

测点表面清理干净并用砂纸磨平，应变片中心贴于测点处，1号应变片贴片情况如图5所示，电路采用四分之一桥加温度补偿方式连接，每次测量一个点的应变值，第一个点试验设备组装后如图6所示。试验过程单点多次测量，多次应变值在（±20）μm内即认为数值在误差范围内可用，图6中，应变测试仪测得1号位置应变片的应变值为（-465）μm，负值表明该测点处压缩状态，查得6061-T6材料弹性模量为70GPa，计算得到该测点的应力值为（-32.55）MPa。

图5 1号应变片情况Fig.5 No.1 Strain Gauge Situation

图6 试验设备Fig.6 Test Equipment

而在仿真模型中，该测点所在位置所对应的仿真应力值为（-29.93）MPa，如图7所示。图7为ANSYS软件中，为了便于观察，将前轮架局部解剖后的俯视图。其他测点方法和步骤同测点1，这里不再累述，最后，将试验所得各测点应变数据换算成应力值后和有限元中对应点仿真应力值做比较，如表2所示。表2中，个别测点误差较高，大于10%，该点为右脚踏靠近转向管处下方，分析原因应是脚踏与转向管焊接处的实物形状与有限元的理想模型形状存在较大偏差所引起，但整体误差在允许范围内，且应力分布情况与仿真一致，因此认为试验与仿真情况基本一致，该有限元模型正确。进一步分析，发现有限元数值普遍小于试验数值，通过划分更细的网格，可略微提高有限元数值使更加趋近于试验值，但提升的数值很小，说明当前网格模型已经收敛，有较高精度，同时考虑巨大的计算成本，对网格不再进行细化操作。

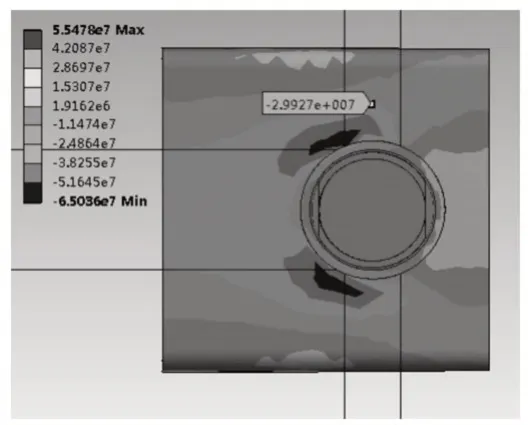
图7 1号测点应力值Fig.7 No.1 Point Stress Value

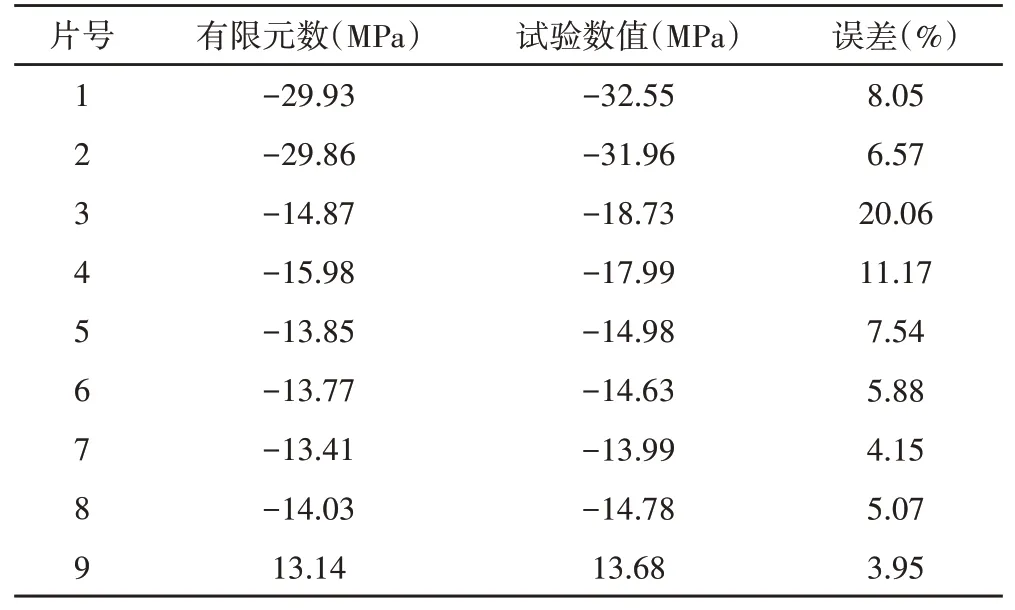
表2 试验数据与有限元数据比较Tab.2 Comparisons Between Test Data and Finite Element Data

4 车架典型工况下受力分析

分析所建立的车架有限元模型在4种典型工况下受力情况，4种典型工况包括满载弯曲工况、弯扭联合工况、紧急制动工况和紧急转弯工况，载荷条件方面，重力以垂直向下的集中力加载，惯性力按相应方向的集中力加载，在承载面上集中力均布，约束条件方面，施加在前、后轮架与轴的连接孔上，具体数值在下文分工况阐述。经求解得到车架在4种典型工况下的应力和总变形云图如图8所示。图8中，由上而下依次满载弯曲、弯扭联合、紧急制动和紧急转弯工况。

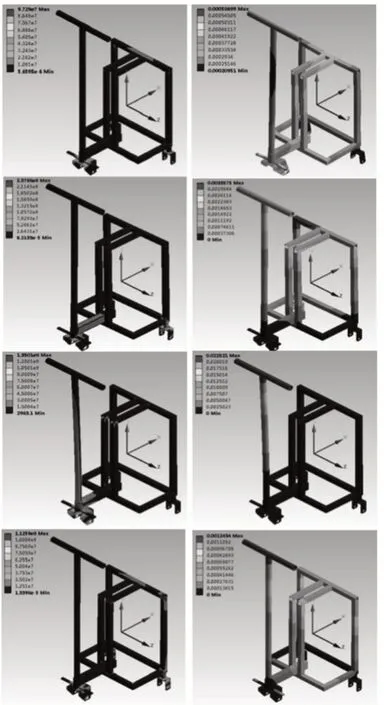
图8 四种工况应力和总变形Fig.8 Stress and Total Deformation of Four Conditions

满载弯曲工况主要模拟行李箱车在良好路面上匀速行驶的情况，满载100kg，按车架自重2kg，行李和电器设备重量8kg，乘坐者体重90kg算，体重80%（720N）施加在车架顶部3根方管处，体重20%（180N）施加在前方脚踏处，行李和电器设备重量（100N）施加在车架底部4根方管上，约束前轮架支撑处X、Y、Z方向平动自由度，约束两个后轮架支撑处Y方向平动自由度，释放所有支点的转动自由度，求解后所得的应力和总变形情况，如图8所示。图8（a）中第一幅图中，最大应力值为97.29MPa，位于前轮转向杆和前轮架焊接处，图8（b）第一幅图中，变形情况被放大30倍以方便观察，最大变形量为0.5mm，位于脚踏端部。

弯扭联合工况模拟行李箱车在凹凸不平路面上行驶时，其中一个后轮悬空的极限情况，加载情况与弯曲工况相同，约束前轮架支撑处X、Y、Z方向平动自由度，约束右后轮架支撑处Y方向平动自由度，释放左后轮架支撑处所有自由度，求解后所得的应力和变形情况如图8所示。图8（a）第二幅图中，应力集中在后轮架、前轮架和伸缩架处，其中右后轮架与圆管连接处应力值最大，达到了237.88MPa，三轮结构在悬空一轮情况下，应力集中到另外2个支撑处，故产生了较大的应力，在图8（b）第二幅图中，因为左后轮悬空，最大变形为左侧座位处，最大变形量为3.3mm。

紧急制动工况模拟在满载情况下以小于20km/h的速度刹车，刹车距离小于3m情况，设以0.5g的减速度制动，按比例施加在握杆、脚踏和座位上，约束前轮架支撑处X、Y、Z方向平动自由度，约束两个后轮架支撑处Y方向平动自由度，释放所有支撑处的转动自由度，求解后所得的应力和变形情况，如图8所示。图8（a）第三幅图中，最大应力值为135.01MPa，位于前轮转向杆近底部处，且应力集中在车架前部结构上，图8（b）第三幅图中，最大变形量为22mm，因制动时身体向前惯性力大部分作用到握杆处，故握杆处变形量较大。紧急转弯工况模拟在满载时车速小于20km/h情况下以0.3g向心加速度沿Z正方向转弯，约束前轮架支撑处X、Y、Z方向平动自由度，约束两个后轮架支撑处Y方向平动自由度，释放所有支撑处的转动自由度，求解后所得的应力和变形情况如图8所示。图8（a）第四幅图中，最大应力值为112.59MPa，位于前轮架处，其次右后轮处也有较大应力，图8（b）第四幅中，最大变形量为1.2mm，位于握杆处。以上4种工况中，应力最大值出现在弯扭联合工况下，为237.88MPa，小于6061-T6材料的屈服极限280MPa，最大变形发生于紧急制动工况下的握杆处，为22mm，在允许范围内，因此该车架满足强度和刚度的使用需求。

5 模态分析

模态分析是研究结构动力特性的一种方法，用于确定结构的固有频率和振型［10］，从而使结构设计避免共振，无阻尼模态分析是经典的特征值问题，动力学问题运动方程为：

式中：[K]-刚度矩阵；θi-第i阶模态的振型矢量；ωi-第i阶模态的固有频率；[M]-质量矩阵。通过有限元软件对该车架进行自由模态分析，获得除刚体模态外的前6阶模态频率如表3所示。

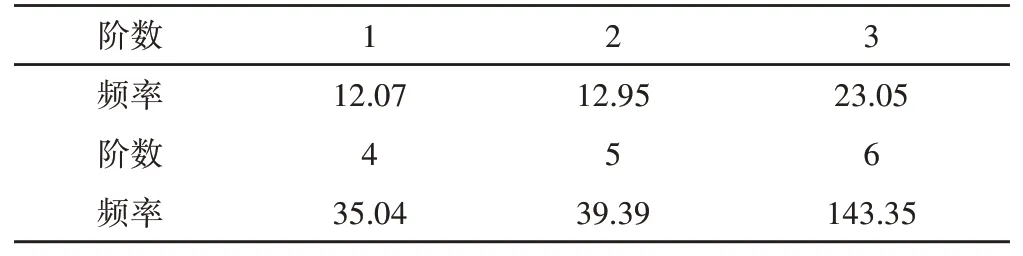
表3 车架自由模态频率Tab.3 Free Modal Frequency of Frame

由于低阶频率对车架的振动特性影响较大，这里只列出前2阶的振型图，如图9所示。

图9 一阶和二阶振型图Fig.9 First and Second Order Vibration Chart

电动行李箱车在行驶过程中来自路面的不平度是引起车架振动的一个重要外部激励，来自路面激励最大值可表示为：

式中：vmax-最大速度；Lmin-路谱值。

根据设定，电动行李箱车以不高于20km/h速度在路况良好的路面上行驶，因此vmax取20km/h，Lmin根据国标路谱，在平坦公路上行驶取值1.0，计算得最大激励值为5.56Hz，比较表4中车架前6阶频率值，可知车架固有频率避开来自路面的激励频率，不会引起共振。电机是引起车架振动的另一个重要原因，根据生产商提供的数据，无刷低速轮毂电机的激励频率小于10Hz，同样避开了车架的固有频率，不会引起共振。

6 结论

（1）设计一款可乘坐、稳定可靠且方便携带的电动行李箱车并建立车架有限元模型，仿真分析该模型在弯曲工况下应力情况，同时制作实物模型进行弯曲工况应力试验，试验数据与仿真结果基本一致，证明该有限元模型精准性。（2）车架在满载弯曲、弯扭联合、紧急制动和紧急转弯4种典型工况下的最大应力值为237.88MPa，小于材料的屈服极限，最大变形量为22mm，在允许范围内，该车架满足使用需求。（3）通过模态分析得到车架前6阶模态频率，可知车架固有频率避开来自路面和电机的激励频率，不会引起共振。（4）车架在前轮转向架和后轮架处应力值较集中，后续有进一步轻量化优化空间。