航空发动机双转子试验台临界转速匹配优化
2021-10-20王东强陈坤旭李明明于贺春
王东强,陈坤旭,李明明,于贺春
(中原工学院机电学院,河南 郑州451191)
1 引言
试验研究作为航空发动机动力学特性研究的重要手段之一,它对于航空发动机的设计、制造等技术研究至关重要,考虑到航空发动机试验研究的高风险和高费用,目前模拟试验台便成为了试验研究的常用方法[1]。随着推重比的提高,航空发动机多为双转子结构,高低压转子间以及转子系统与机匣的耦合影响日益增加,构成了较复杂的动力学特性[2]。因此对以航空发动机动力学特性为研究对象的试验台架而言,进行一定程度的简化非常有必要,但简化必然会带来各种误差,为了更真实的反映航空发动机的动力学特性,需保证基于简化模型建立的试验台动力学特性与航空发动机动力学特性基本一致,其对航空发动机转子动力学实验领域的研究工作具有重要意义,也为后续的理论分析和实验规律的探索建立了基准。对双转子系统进行临界转速的分析,是进行双转子系统动力学分析的基础,临界转速的计算正确与否,直接影响后期双转子系统的瞬态响应、稳态响应、不平衡响应、稳定性分析、碰摩振动特性,以及不对中等动态特性的分析,因此,急需一种简便、快速计算航空发动机双转子试验台与航空发动机原型机临界转速相匹配的优化算法,以便可以更好地对航空发动机的动力学特性进行试验研究,同时也可缩短双转子试验台的设计周期。
从已公开的文献来看,目前国内外,现有的航空发动机试验台大多是单转子试验台,双转子试验台较少。此外,与国内的转子试验台相比,国外的转子试验台超临界运行的工作转速比国内的高很多。
同时,研究双转子试验台与航空发动机临界转速匹配性优化的文献也较少。如文献单转子试验台主要对航空发动机低压轴进行优化研究,转子的最高转速达到7900rpm[3];文献单转子试验台按Rolls-Royce RB401航空发动机进行设计,转子的最高转速为6000rpm[4-5];文献建立的单转子试验台主要通过调节转子的弹性支撑从而研究转子的临界转速[6-7];文献采用了能够满足试验要求的单轮盘、两端支撑的单转子试验台,转子的临界转速主要是通过更换不同的轮盘来调节,额定转速为12000rpm[8];文献利用结构比较简单的单轮盘、两端支撑的单转子试验台研究转子的碰摩故障,速度较低[9];文献研究中心的试验台为小型转子试验台,主要是用于气箔轴承动力学特性研究,运行速度为20000rpm[10-11];文献[12]和文献[13]建立的试验台为双转子试验台,其能达到的最高转速都较小;文献[14]的双转子试验台较小,长度不超过1m;柏林工业大学的双转子试验台的高低压转子的工作转速相对较高,分别为12500rpm和6000rpm[15-16]。
文献应用ANSYS有限元软件计算了双转子系统的临界转速以及振型[17];文献建立了双转子轴承系统的动力学模型,研究了不同转速比情况下双转子系统的临界转速[18];文献以转子-轴承系统的不平衡响应幅值为优化目标,优化了该系统的临界位移,研究对象为单转子系统[19];文献以多阶临界转速及动力响应为约束变量对一单转子系统的多阶振型进行了优化[20];文献运用混合遗传算法对一转子系统的临界转速进行了优化设计,优化对象为单转子系统[21]。
文献以大型汽轮发电机组为研究对象,计算了其临界转速,研究了单转子系统的优化设计[22];文献以球轴承-转子系统为研究对象,对该系统的固有频率与临界转速的分析及其结构的优化进行了研究[23];文献在多支撑转子-轴承系统试验台设计的过程中,为了更好的反映多支撑轴承-转子系统的动力学特性,尽量保证试验台的前三跨转子前两阶临界转速与实际转子一致,研究对象仍为单转子系统[24];文献在风扇转子试验器的设计中,逐个分析了转轴内外径、轮盘外径与质量、轴承的刚度对试验器临界转速的影响,通过调整这些参数实现试验器临界转速等特性的控制[25];文献提出了一种双转子实验台结构,逐个分析了支承刚度、转速比、轮盘的极转动惯量、长径比等因素对台架临界转速的影响,并据此对实验台架的临界转速做了调整[26];文献逐个分析了转子的支撑方式、支点跨距、转轴直径大小、转子质量分布以及支撑刚度对试验器转子的临界转速的影响,据此对试验台转子各阶临界转速进行了调节[1]。
综合上述文献,国内外高校和研究院所搭建的航空发动机实验平台大部分都只遵循结构相似原则,对于模拟汽轮机和涡轮的轮盘在转子上的定位比较随意,计算得到的双转子临界转速与航空发动机临界转速的实测值存在着较大的误差,双转子试验台的尺寸普遍较小,转速相对较低;双转子系统临界转速优化过程中多单独根据一组设计参数进行逐步优化,按照该方法再分析某个参数对其临界转速的影响,进行调节时会对多阶临界转速都会施加影响,逐个参数的反复调节必然会消耗大量的时间;另外现代航空发动机向高速化和柔性化方向发展,尤其是中小型航空发动机,更多地使用薄壁板壳结构,具有复杂而密集的振动模态,转子工作转速往往位于其几阶临界转速以上,单纯通过经验和试凑进行多阶临界转速匹配性优化,工作量过大,可靠性也不易保证。
鉴于此,提出了双转子试验台和航空发动机原型临界转速匹配性优化方法,研究对象为某型号航空发动机双转子,低压转子额定工作转速为12000rpm,高压转子额定工作转速为15000rpm,根据其支撑方式和结构形式,搭建了其转子-轴承-机匣耦合系统简化模型,基于有限元方法求解了模型临界转速,运用变换哈墨斯利算法实现模型与原型机临界转速匹配性优化。
2 双转子航空发动机整体动力学模型
2.1 转子模型
根据某型号航空发动机的支撑方式和结构形式等建立转子-轴承-机匣耦合系统简化模型,如图1所示。该系统的支撑结构为五点支撑,轴承支撑的编号从左到右依次是2,6,10,13,编号10为中介轴承,轴承选用航空发动机同类型轴承,编号2处轴承类型为深沟球轴承,编号6和10处轴承类型为角接触球轴承,编号10和13处轴承为圆柱滚子轴承,系统由低压转子、低压压气机模拟盘、高压转子(空心)、高压压气机模拟盘、高压涡轮模拟盘及动力涡轮、低压涡轮模拟盘和机匣组成、高压转子和低压转子靠中介轴承连接。

图1 转子-轴承-机匣耦合系统简化模型Fig.1 Simplified Model of Rotor-Bearing-Casing Coupling System
为了使得模型的复杂程度减小,方程的求解更高效,模型的建立过程中遵循以下假设:
(1)低压转子和高压转子由于都具有较大的长径比,因此可用Timoshenko梁单元表示,只考虑这些转子轴的横向弯曲振动,不考虑转子轴的扭转振动和轴向振动。
(2)假设转盘以及转子轴的材料是均匀连续和各向同性的,并在弹性范围内服从Hook定律。
(3)低压压气机、高压压气机、高压涡轮、动力涡轮以及低压涡轮都以模拟盘的形式表示,以集中质量和转动惯量的形式作用于模拟盘的质心上,考虑盘的陀螺效应。
(4)假设在工作速度范围内机匣和转子轴产生弯曲耦合,其横截面的形状为圆形,故可将机匣按照固定的梁单元表示。
(5)轴承被简化为弹簧-阻尼系统,不考虑轴承的交叉刚度。
2.2 模型运动方程
从图1可知,模型的绝对坐标系为o-xyz,坐标轴o-z与高压转子和低压转子的轴线重合,建立的转子-轴承-机匣耦合系统简化模型主要包括模拟盘、柔性轴、机匣和支撑四类部件,根据文献[27]、[28]按照部件类型完成单元动力学方程的建立,根据力学关系进行部件组装,最终得到转子-轴承-机匣系统整体运动微分方程。
2.2.1 模拟盘
模拟盘假设为刚性圆盘,不考虑其应变能,仅考虑其动能,取模拟盘的横向线位移为x,y和夹角θx,θy为广义坐标。设盘的质量为md,直径转动惯量为Jd,极转动惯量为Jp,求取模拟盘的动能,运用Lagrange方程得到模拟盘的运动方程为:

式中:Md-模拟盘的质量矩阵,J-陀螺矩阵,模拟盘轴心的广义位移向量为q1d=[x,θy]T,q2d=[y,-θx]T,Q1d和Q2d为相应节点处的广义力向量包括不平衡力、圆盘相邻轴段的力和力矩以及支撑的约束力等。则上述矩阵可以表示为:
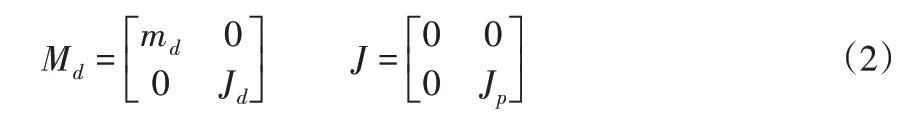
2.2.2 轴段微分方程
建立轴段单元如图2所示,取轴段AB两端的节点的位移为广义坐标即:
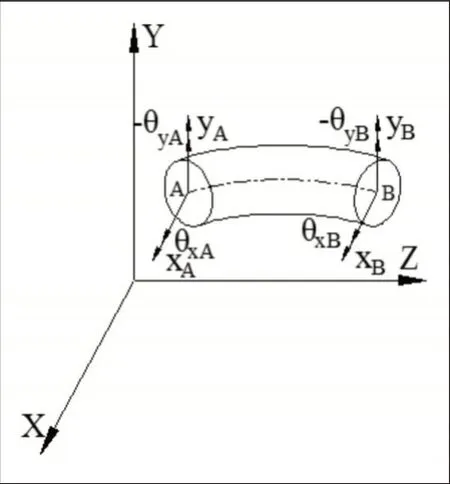
图2 弹性轴段Fig.2 Elastic Shaft Segment

通过Lagrange方程可以得到轴段AB在给定坐标系下的运动微分方程为:
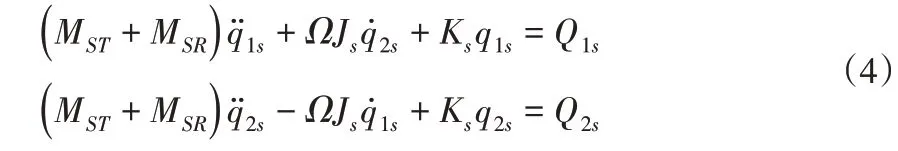
式中:MST-轴段的单元移动惯性矩阵;MSR-单元转动惯性矩阵;Ks-单元刚度矩阵;Js-单元回转矩阵;Q1s和Q2s-广义力向量;设轴段的长度l,轴截面的面积为A,轴的半径为r,密度为ρ,轴段的单位长度的质量为α即α=ρA,则上述单元矩阵可以表示为:

2.2.3 轴承运动微分方程
如图3所示,假设轴承座中心的节点处的坐标为xs,ys,对应的轴径中心节点的坐标为xj,yj,则轴承座的运动方程为:
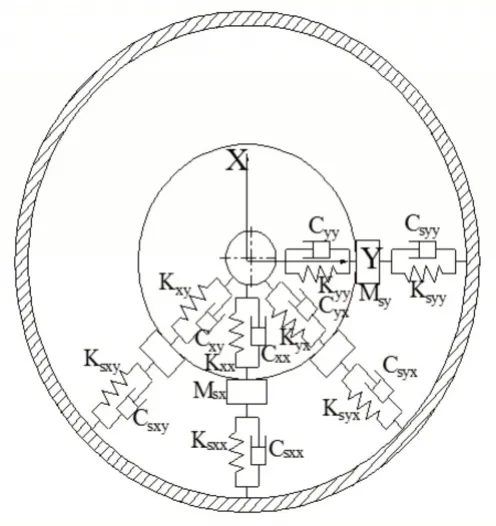
图3 轴承模型Fig.3 Bearing Model

2.2.4 机匣运动微分方程
机匣运用固定的梁单元进行建模,考虑了其剪切效应和转动惯量,采用有限元法可以得出机匣的运动方程为:

2.2.5 系统运动微分方程
按照高压转子、低压转子、模拟盘、轴承以及机匣之间耦合节点的对应关系,以及界面上的力的相互作用关系,从而合并各类部件的运动方程,便可以得出双转子系统的运动微分方程为:
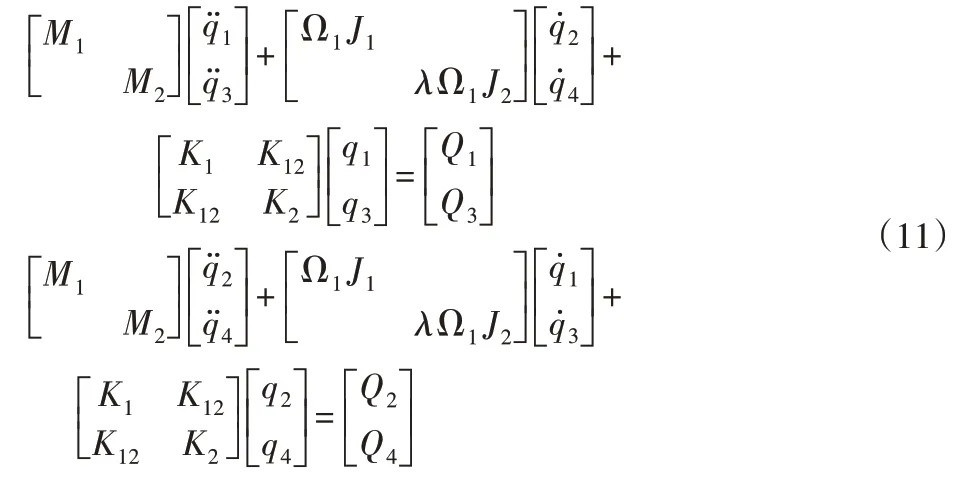
式中:M1、M2-高低压转子系统的总质量矩阵;K1、K2-高低压转子系统的总刚度矩阵;Ω1J1、Ω2J2-高低压转子系统的总陀螺矩阵;Q1,Q2,Q3,Q4-外部激励;h、l-高低压转子的节点数,Ω1和Ω2-高低压转子的转速,令λ=Ω2/Ω1即低高压转子转速比,K12-中介轴承10所产生的耦合刚度可表达为:
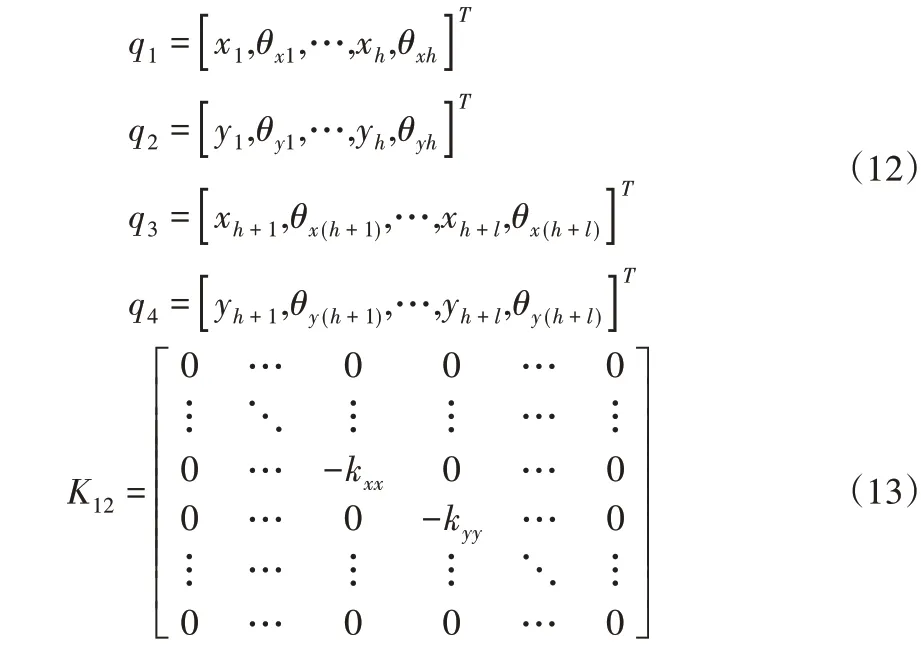
式中:-kxx、-kyy-(4q-3,4p-3)和(4q-2,4p-2)处;p和q-中介轴承节点对应的高低压转子节点数。
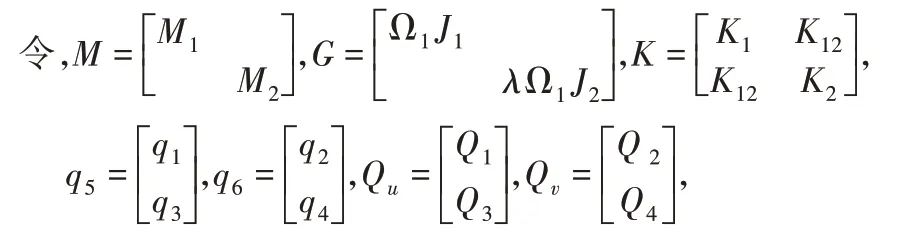
则,系统运动微分方程可以表示为:

令,Qu=0,Qv=0则可以得到系统微分方程对应的齐次方程的解为:

将方程(15)代入方程(14)可以得出:

从而得到频率方程为:

根据式(17)便可以求出当Ω1=ω时,转子-轴承-机匣耦合系统的临界转速,此时得出了高压转子为主激励时系统临界转速。
3 转子系统临界转速计算

表2 高压转子轴参数表Tab.2 Parameters of High Pressure Rotor Shaft

表3 模拟盘参数表Tab.3 Parameter Table of Analog Disk
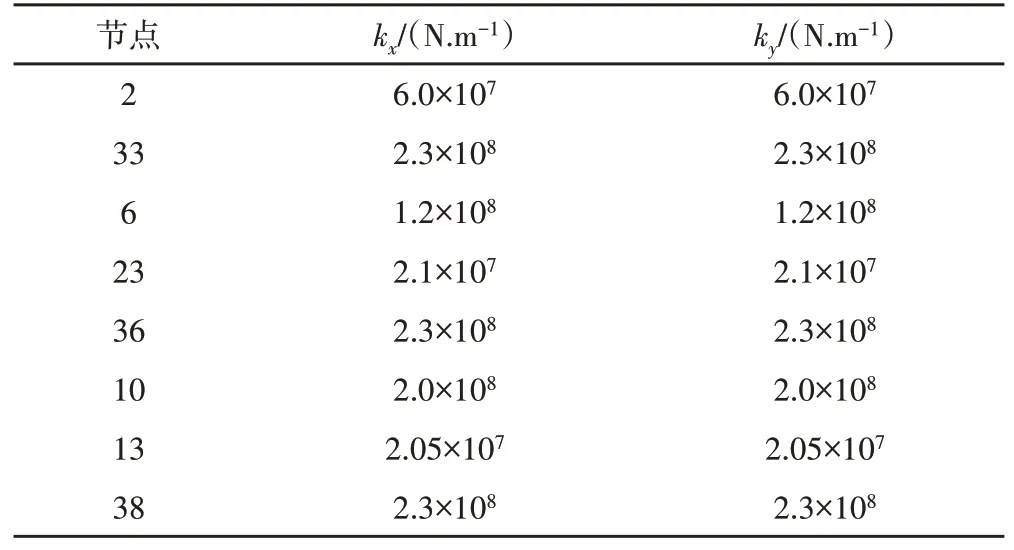
表4 弹性支撑参数Tab.4 Elastic Support Parameters
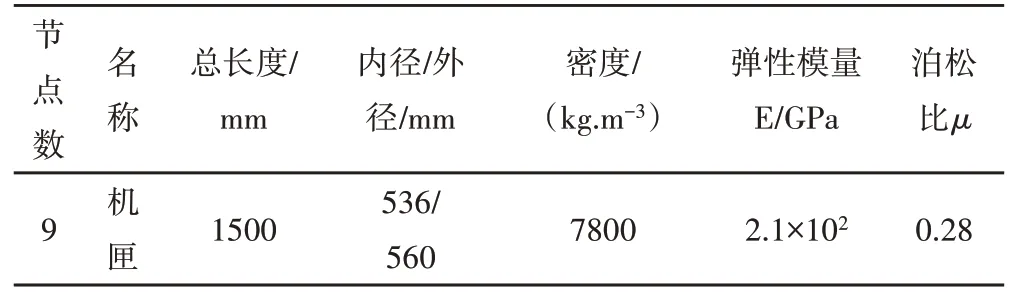
表5 机匣计算参数Tab.5 Casing Calculation Parameters
结合图1所示的转子-轴承-机匣耦合系统模型,根据表1~5中的计算参数,编写系统临界转速计算程序,高压转子与低压转子的转速比为1.25,分别得到以低压转子为主激励和高压转子为主激励的双转子系统坎贝尔图,如图4、图5所示。

表1 低压转子轴参数表Tab.1 Parameters of Low Pressure Rotor Shaft
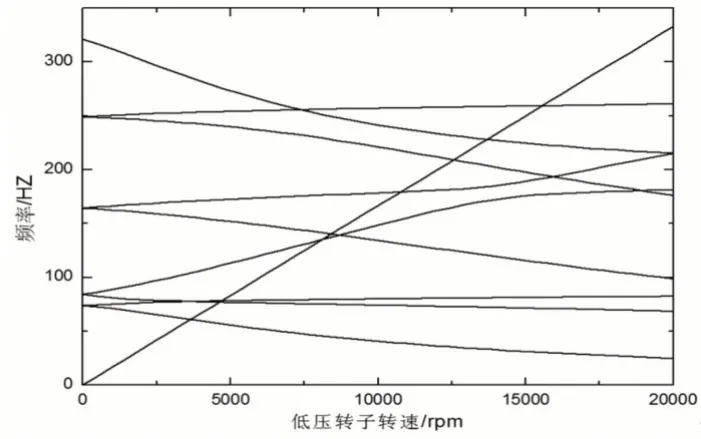
图4 低压转子为主激励的坎贝尔图Fig.4 Campbell Diagram with Low Pressure Rotor as Main Excitation
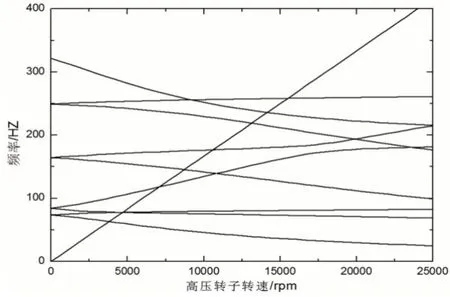
图5 高压转子为主激励的坎贝尔图Fig.5 Campbell Diagram with High Pressure Rotor as Main Excitation
如图4所示,表示了高低压转子以1.25的转速比运转,转子整体系统的正反进动曲线随低压转速变化图,图5则表示转子整体系统的正反进动曲线随高压转速变化图。根据临界转速的定义,等速线与正进动曲线的交点即为临界转速值,得到模型由高低压转速激起的前四阶临界转速计算结果,如表6所示。
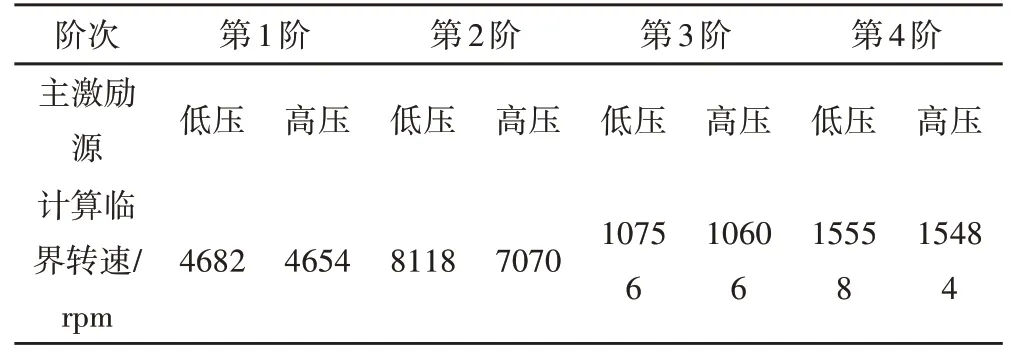
表6 简化模型临界转速计算结果Tab.6 The Critical Speed Calculation Results of the Simplified Model
4 航空发动机临界转速测试
模型的简化必然会带来误差,为了对比模型临界转速与实测数据的误差以及为后续临界转速优化建立基准,通过三维转速谱图分析法,对航空发动机整机的临界转速进行了测试。
4.1 测点分布与测试系统
测点分布如图6所示,共放置5个传感器,1和3测点分别为风扇前支点和中介机匣位置,放置磁电式速度传感器,2、4和5测点分别为附件机匣位置、减速器和低压涡轮支点,放置三向加速度传感器,信号采集设备为美国DP信号采集系统,整机测试系统如图7所示。

图6 航空发动机整机测点布置Fig.6 Layout of Measuring Points for the Whole Aircraft Engine

图7 航空发动机整机测试系统图Fig.7 Test System Diagram of Aircraft Engine
4.2 测试结果及其与计算结果误差分析
测试得到三维转速谱图,其横坐标为频率,纵坐标为以一定转速相隔的响应功率谱,从图中的功率谱曲线峰值走向以及变化情况便可以初步确定临界转速范围,若峰值组成的“山脉”的振动频率与转速成正比关系,且在某一转速范围内其峰值明显,则该转速即为临界转速,根据该判断方法,便得到整机临界转速,测试结果及其与模型计算结果的误差,如表7所示。

表7 实测临界转速及其与模型计算结果误差Tab.7 Measured Critical Speed and Its Error with Model Calculation Results
从表7可知简化模型的临界转速与航空发动机实测数据高阶临界转速相差较大,超过了允许误差5%,为了满足两者动力学特性的相似性,需要对模型的临界转速进行优化。
5 转子系统临界转速优化
在临界转速不满足设计要求时,可改变转子系统的结构参数,例如转轴的长度、直径、轮盘的尺寸等,或者轴承以及机匣的支承刚度,从而实现模型临界转速的调整[21]。为了更真实的反映航空发动机动力学特性,轴承选用航空发动机同类型轴承,不改变系统支撑刚度以及轴的直径。根据表7中的数据,模型的高阶临界转速需进行较大程度的调整,由于轮盘的转动惯量所产生的陀螺效应对转子的高阶临界转速影响较大,因此优化轮盘的大小对于调节转子的临界转速具有重要作用[1]。此外由于试验台场地的限制,转子轴长度需满足一定约束条件。考虑到采用人工调整的方式进行调节,无法保证优化的效率及准确性,采用变换哈墨斯利(Shifted Hammersley)算法对模型的临界转速进行优化。
5.1 变换哈默斯利算法构建原理
变换哈墨斯利算法优化方法是一种适用于所有类型样本生成的一种抽样方法,根据根逆函数构建而成,过程如下:
任何整数n都可以用下面的公式表示为一个数字序列n0,n1,n2,……,nm

如果一个整数用基数R表示,则式(18)可表示为:

逆根函数是指通过对式(19)中的关于小数点的数字顺序进行倒转,从而得到(0,1)中的分数的函数如下:
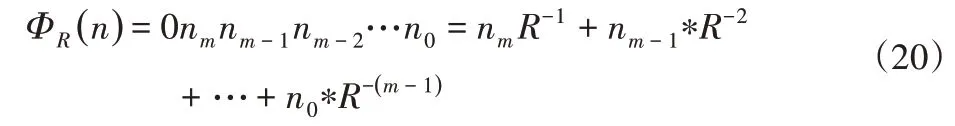
因此,对于k维搜索空间,Hammersley点由以下公式给出:

其中,i=0,…,N表示样本点,为了使得Hammersley采样器生成的点更靠近k维超立方体的原点,提出一个点移动过程,将所有Hammersley点按式(22)进行移动

5.2 临界转速优化设计模型
假设系统目标函数为分别以高低压转子为主激励的临界转速,0<nh1<nl1<nh2<nl2<nh3<nl3<nh4<nl4,nhi和nli分别是以高低压转子为主激励的第i阶临界转速,约束变量为低压转子轴的长度,lil<li<liu(i=1,2,…,s),lil和liu分别为约束变量的上下限,ckl<ck<cku(k=1,2,…,t),ckl和cku分别为设计变量的上下限,则该优化问题可以表达为:式中:n*hi、n*
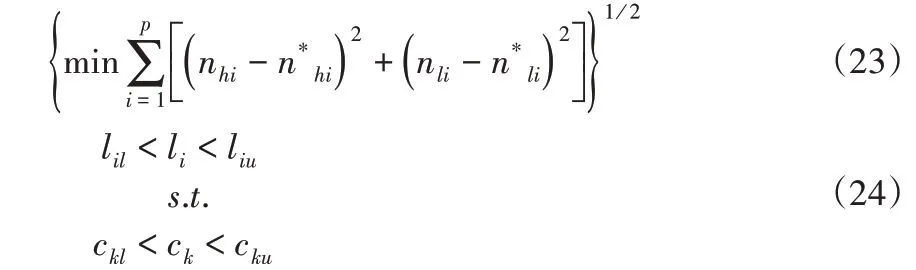
li-优化目标函数值即分别以高低压转子为主激励的实测临界转速值。
5.3 灵敏度分析
优化的目标函数为系统中分别以高低压转子为主激励的前四阶临界转速,目标值为航空发动机真机的实测数据,设计变量为低压压气机、高压压气机、高压涡轮、动力涡轮、低压涡轮的转动惯量,考虑到试验台场地的限制,将低压转子的轴段长度也同时作为设计变量,由于低压转子的轴段数较多,考虑到实际工况,排除左右两端的联轴器连接轴段,选择如图8所示的各轴段长度进行灵敏度分析。首先建立灵敏度分析的数学模型,设α为系统临界转速值,β1、β2、…、βm为转子系统的各个参数值,则系统的特征方程为:

图8 低压转子部分轴段长度Fig.8 Length of Shaft Segment of Low Pressure Rotor Part

对公式(25)两边微分可以得到:

由式(26)可得,系统的参数的增量是δβk(k=1,2,…,m),其临界转速的微小增量是δα,其转子系统的特征行列式的改变量是δΔ。
令δβj≠0,δβk=0(k≠j,k=1,2,…,m),αl为转子系统某一阶的临界转速,则式(26)可表示为:

若δΔl=0,则转子系统的灵敏度值为:

根据sl j的数值,便可以得出对转子系统临界转速影响较大的参数。对图8所示的各个轴段长度进行灵敏度分析,其结果如表8所示。
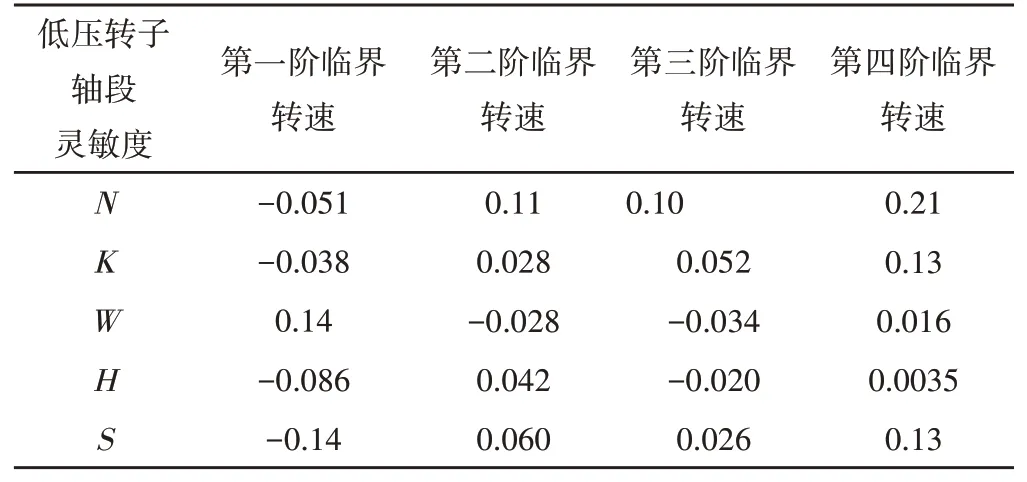
表8 低压转子轴段灵敏度分析结果Tab.8 Sensitivity Analysis Results of Low Pressure Rotor Shaft Segment
表中的系统灵敏度为无量纲,负号表示随着系统参数增大,系统临界转速减小,轴段单位为m,临界转速单位为rpm。由于优化的目的是缩短低压转子轴段长度,减小高阶临界转速,因此灵敏度选择标准为较大的正值,综合分析表中数据知N、K、S三段的灵敏度分析结果较符合选择标准。
5.4 临界转速优化过程
系统优化流程,如图9所示。根据初始数据建立了转子-轴承-机匣耦合系统的有限元模型,求解系统的临界转速,优化进行之前设定了优化目标优先顺序以及允许优化误差,设定了约束变量以及设计变量范围,优化过程中,根据优化算法进行设计变量的修改,再依次进行优化结果评估和判断是否满足约束条件的要求,若有一者不满足,则重新修改设计变量,若两者都满足,则输出解,若所有样本数据都无法满足,则重新定义设计变量的取值空间,重新进行优化计算,直到找到符合要求的解集,最后根据优化目标的优先顺序得到最优解。
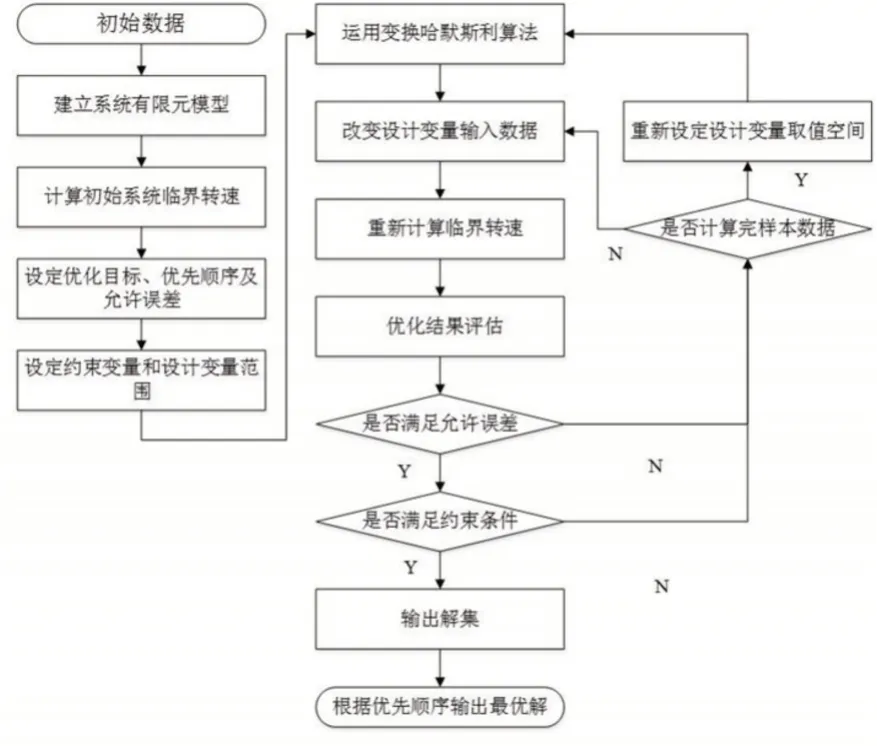
图9 系统优化流程图Fig.9 System Optimization Flow Chart
6 优化结果分析
优化完成后得出转子分别以高低压转子为主激励的坎贝尔图如图10、图11所示。从而得到分别以高低压转子为主激励的临界转速及其与实测数据的误差,如表9所示。系统的设计参数的优化结果,如表10所示。

图10 优化后低压转子为主激励的坎贝尔图Fig.10 Campbell Diagram of Optimized Low Pressure Rotor with Main Excitation
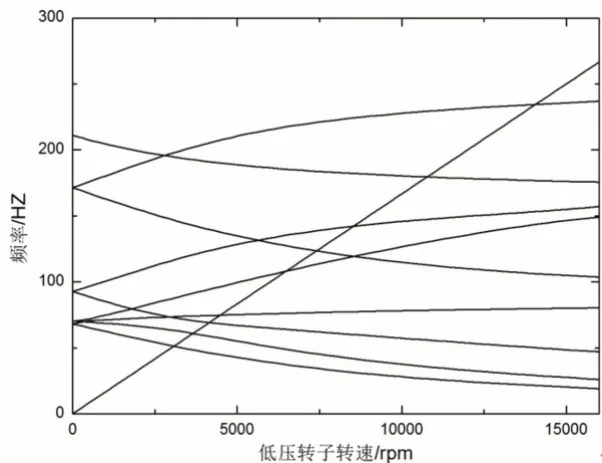
图11 优化后高压转子为主激励的坎贝尔图Fig.11 Campbell Diagram of Optimized High Pressure Rotor with Main Excitation

表9 系统临界转速优化结果Tab.9 System Critical Speed Optimization Results
由表9和表10可得出系统临界转速优化结果与航空发动机真机实测数据相差较小,远小于允许误差,优化后低压转子的长度比优化前低压转子长度减少了9.7%,满足了设计要求。从表中数据可以得出根据优化后参数进行试验器的设计可以很好的反映航空发动机真机的动力学特性,从而为后续的理论分析和实验规律的探索建立基准。
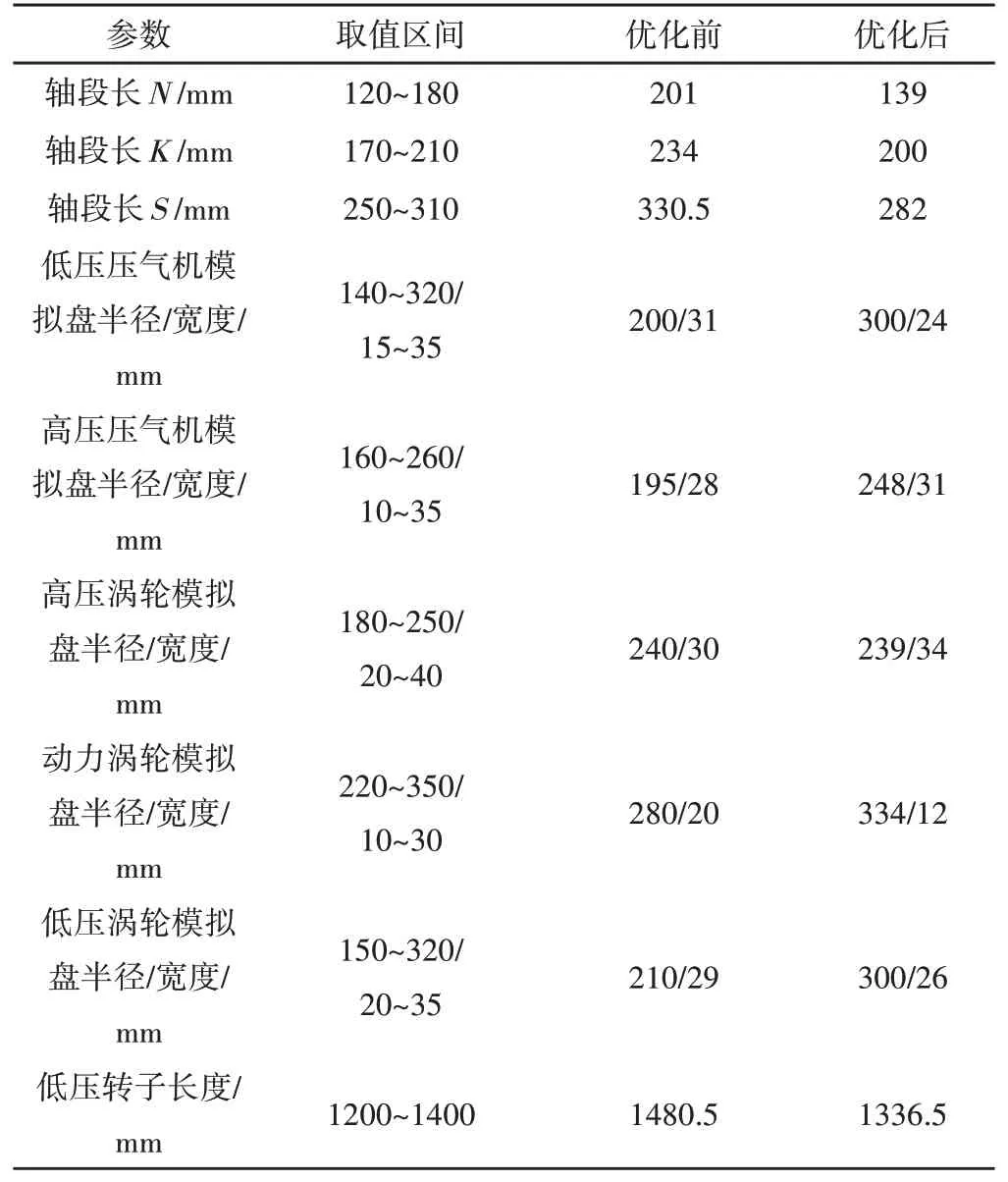
表10 系统设计参数优化结果Tab.10 Optimization Results of System Design Parameters
7 结论
基于航空发动机的结构,建立了转子-轴承-机匣耦合系统的简化模型,运用有限元方法求解了高低压转子转速比为1.25时系统的临界转速,为了满足计算结果与实测数据的匹配,结合变换哈默斯利算法进行了临界转速的优化。结果表明,双转子试验台的临界转速和航空发动机实测数据误差在5%以内,优化后低压转子的长度比优化前低压转子长度减少了9.7%,满足了设计要求,简化模型可以较好的反映航空发动机真机的动力学特性,证明了该优化方法的有效性,对航空发动机试验台的设计具有指导意义。
