基于大涡模拟的风力机尾流特性研究

杨从新，张亚光，张旭耀，何 攀

（1.兰州理工大学能源与动力工程学院，甘肃 兰州730050；2.甘肃省流体机械及系统重点实验室，甘肃 兰州730050）

1 引言

风力机尾流中存在叶尖涡、叶根涡等复杂的涡系，它们之间存在大尺度相干结构决定的分离流动，对风力机组的安全运行提出挑战，研究风力机尾流特性，对合理开发与研究新型风力机和合理利用风资源有重要指导作用。近年来，大涡模拟在风力机尾流与风场的高精度数值模拟中的应用越来越广泛。文献［1］首次耦合大涡模拟与致动线方法研究风力机尾流。文献［2］用致动线方法研究了均匀来流条件下的风力机近尾流特性，对涡结构、速度亏损、拟涡能进行分析，验证了致动线模型的准确性。文献［3］将致动线方法的数值模拟结果与BEM理论、CFD方法以及风洞实验进行了系统的比较，验证了致动线方法用于风力机气动数值模拟的可行性。文献［4］基于Lagrangian动力亚格子模型对风力机尾流场进行数值模拟，分析了风力机近尾流场与远尾流场的流动特性。文献［5］利用致动线方法分析了不同入流条件下风切变、湍流强度等因素对风力机尾流特性的影响。文献［6］对充分发展的风电场边界层进行数值模拟，发现高雷诺数流比低雷诺数时对SGS模型的选择更敏感。文献［7］引入周期性扰动，研究了小型风力机叶尖涡的稳定性及其演变，发现周期性扰动的存在对涡旋的发展与破碎过程有明显的影响；在涡旋破裂前，还观察到了明显的涡旋配对现象，并通过改变强迫扰动的幅值和频率进行了参数研究，评价其对叶尖涡的影响。文献［8］对水平轴风力机在水槽中的近尾流进行实验研究，探讨了水平轴风力机尾迹的旋涡相互作用及螺旋形涡丝的稳定性。文献［9］对单台风力机进行数值模拟研究，受叶尖附近的低振幅激发源的扰动，沿螺旋运动的波的放大会触发不稳定，导致尾流破碎，重点研究了从叶片后缘脱落涡的稳定性。

以上研究使用单一湍流模型对风力机进行模拟，不同亚格子模型的选取会对研究对象数值模拟的结果产生影响。这里以流场中的单一风轮为研究对象，排除塔架、机舱等结构对风力机尾流的影响，探讨均匀入流条件下采用三种亚格子模型的风力机尾流特性。

2 研究对象与计算方案

2.1 研究对象

以一台33kW两叶片水平轴风力机为研究对象，由于尾流的旋转效应，叶尖使用Glauert修正，风力机基本参数如表1所示。

表1 33 kW风力机基本参数Tab.1 The Parameters of 33 kW Wind Turbine

2.2 计算方案

计算域及加密区域网格尺寸，如图1所示。图中：D-风轮直径。风轮位于进口后方2D处，为减少壁面效应，根据文献［10］提出的准则，设置计算域尺寸为22D×6D×6D；同时，为减小流动方向网格加密界限处不同网格尺寸对计算结果的影响，网格加密区域为入口到出口，沿风轮径向经过二次加密后的六面体网格总数为4.356×107，最小网格尺寸为0.25m。

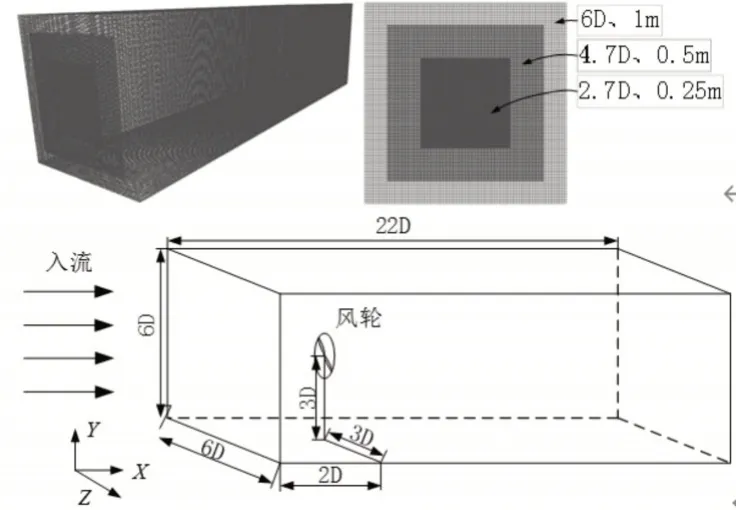
图1 计算域及网格加密Fig.1 Computing Domain and Mesh Refinement

计算时间步长为0.005 s；大涡模拟对亚网格尺度流动进行模拟，重点关注尾流涡结构，无需进行网格无关性验证。这里数值计算中风力机叶尖速比l分别取值13.17、8.23、5.98，对应入流速度分别为5、8、11 m·s-1。

3 数值模型

耦合致动线与大涡模拟方法，采用开源CFD软件Open-FOAM对处于均匀入流条件下的风力机做数值模拟研究。

3.1 致动线方法

风力机的模拟用致动线方法，其基本概念为每个风力机叶片用一条承受体积力的线表示，将叶片沿展向分割为若干叶素，分别求解叶素上的体积力。叶素上的升力、阻力由下式计算为：

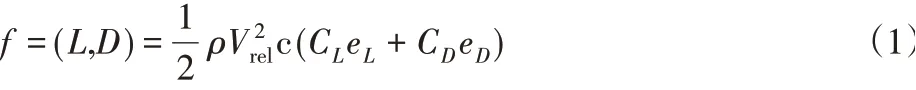
式中：eL-升力方向向量；eD-阻力方向向量。

各致动元上离散的点力通过高斯正则化函数将致动力反作用于流体：

点（x，y，z）处的体积力为：

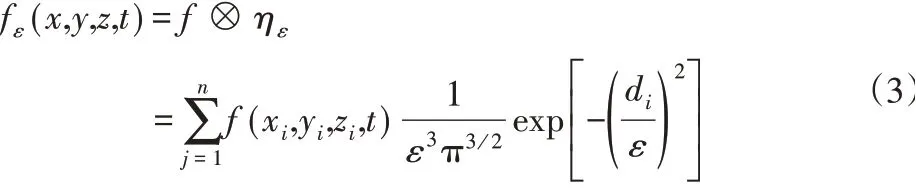
式中：di-第i个致动点（xi，yi，zi）的中心与投射点（x，y，z）的距离；ε-高斯光顺参数。

致动点处网格尺寸为0.25m，高斯光顺参数ε=0.5，风轮直径上分布致动点个数为n=60，以使致动点间的距离小于风轮处网格尺寸。

3.2 大涡模拟

对Navier-Stokes方程施加卷积过滤运算，滤波后的LES控制方程如下：

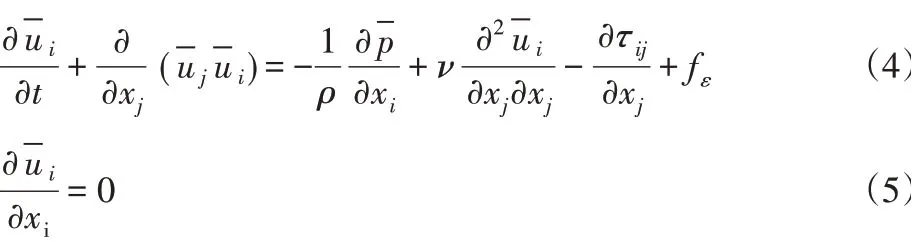
式中：ρ-空气密度；ν-分子粘度滤波后的速度分量；p-修正压力；fε-由于风轮的存在作用于空气的体积力；τij-SGS应力，定义为

3.3 湍流模型

3.3.1 Smagorinsky模型

计算亚格子应力τij有不同的方法，常用的方法是利用Boussinesq涡粘假设。将τij表示为正应力与偏向应力，正应力部分被认为各向同性，求解Smagorinsky模型的表达式为：

正应力和亚格子动能kSGS联系起来，则：

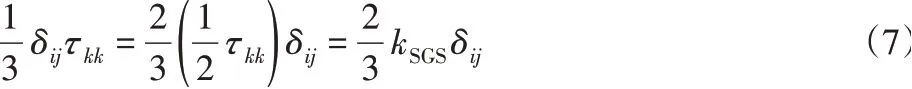
所以，亚格子应力可表示为：

式中：δij-克罗内克符号，当i=j时δij=1，i≠j时δij=0；

νSGS-亚格子尺度粘度应变率张量。

Smagorinsky模型中，νSGS表示为：

将上式代入方程（8），则方程封闭参数为kSGS，

式中：Ck、Ce-Smagorinsky模型无量纲系 数，Sm模型取值Ck=0.0676、Ce=0.93；Δ-滤波器过滤尺度。

3.3.2 Lagrangian动力模型

亚格子动力模型对Navier-Stokes方程施加两次过滤尺度不同的过滤运算，从解析流中动态计算模型参数，并允许模型参数在空间和时间上发生变化，亚格子动力模型基于Germano等式：

求SGS模型系数Cs的动态过程使Germano等式误差最小化：

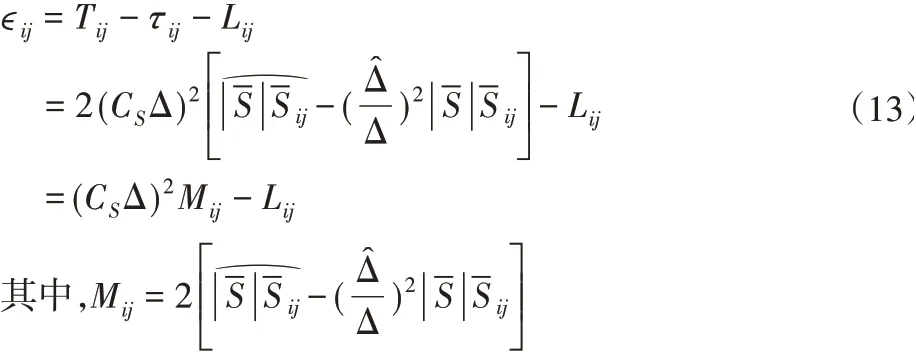
由文献［11］等人提出的初始动态模型满足ϵijSij=0得到Cs。文献［12］发现，当ϵij在最小二乘法上最小化时，方程表现良好，从而得到结果：

式中：“＜＞”-系综平均。

文献［13］提出了Lagrangian动力亚格子模型，该模型沿流体质点运动轨迹做统计平均最小化Germano等式误差。

本次数值实验采用以下亚格子模型进行数值计算：Smagorinsky模型（Smagorinsky model）、Lagrangian动力模型（Lagrangian dynamic model）；另外当νSGS=0时没有明确表示湍流粘性，此时引起动能耗散的唯一影响因素是数值耗散。以上三种模型在这里中分别以Sm（Smagorinsky model）、dyL（Lagrangian dynamic model）、Nom（No model，νSGS=0）表示。

3.3.3 数值离散与边界条件

采用开源软件OpenFOAM进行数值计算，N-S方程中的原始变量用有限体积法进行离散，求解方程时使用瞬态压力全隐分离式（PISO）算法。时间项采用二阶有界隐式Crank-Nicholoson格式，梯度项、散度项等空间项采用高斯线性离散。进口为速度入口，方向沿X轴，出口为压力出口，壁面处采用滑移边界条件。

4 计算结果分析

本次数值实验采用甘肃省计算中心高性能计算集群的两节点48核心计算，其中，计算工况λ=13.17时，设置总计算时间为110s，三种亚格子模型分别花费计算时间180.7h（dyL）、140.2h（Sm）、158.8h（Nom）。亚格子动力模式需要进行统计平均，理论上需要进行系综平均，非常花费计算时间；但拉格朗日动力模式沿质点轨迹平均确定模型系数，增加的计算量不多。当尖速比l分别取值13.17、8.23、5.98时，对应的风轮输出功率为8.016、16.623、33.267 kW，额定风速下的功率误差为0.809%，满足计算要求。当叶尖速比l=13.17时，三种SGS模型在计算过程中的最大库郎数Co（Courant Number）分别为0.135（dyL）、0.136（Sm）、0.149（Nom）。

4.1 尾流发展

Lagrangian动力模式允许在不调整任何参数的情况下，根据流动在时间和空间上的变化，对模型系数和参数进行动态计算。由于涡粘模型对涡生成的直接影响，不考虑轮毂、塔架、机舱等对风力机尾流的影响。

由图2（a）可知，尾流从叶尖涡与叶根涡以近似对称的涡旋结构向下游传播，在远尾流区，由于流体具有粘性，在周围气体的作用下尾流的对称结构被打破。叶片失速前，λ=8.23、l=5.98时随叶尖速比减小，攻角增大，叶片吸力面与压力面间的压差增大，导致叶尖涡更强具有较高的稳定性。λ=13.17时，尾流区呈现完整的近尾流区、尾流发展区与远尾流区，从尾流发展的角度看具有代表性，将主要对此工况下不同SGS模型的风力机尾流进行研究。

如图2（b）所示，为λ=13.17时使用不同SGS模型获得的垂直于风轮旋转平面的涡旋云图。近尾流区，尾涡从叶尖与叶根处向下游传播；之后三种亚格子模型下的叶尖涡均出现了K-H（Kelvin Helmholz）不稳定性现象，与文献［14］中实验观测到的叶尖涡横截面尾迹相似；最后由于湍流的能量级串，大尺度尾涡在远尾流区耗散变成小尺度涡。

图2 使用dyL模型垂直于风轮旋转平面的涡旋图Fig.2 2D Snapshots with Vorticity Contour in the Vertical Plane in dyL Model

4.2 尾流速度分布及其湍流特性

实际流体中，由于流体具有粘性，尾流终将恢复；数值模拟中，由于数值耗散，尾流也终会恢复。由图3中使用dyL模型在不同叶尖速比下的速度分布曲线可知，λ=5.98时，直到风力机尾流下游11D处速度有微弱减小；λ=13.17时尾流恢复最快。由于周围空气的作用，尾流逐渐膨胀发展为完全湍流。从三种SGS模型预测的尾流速度分布曲线（图4）可以看出，0D-2D之间的近尾流区，不同SGS模型预测的尾流速度廓线几乎相同，在尾流发展区与远尾流区，三种SGS模型预测的尾流速度廓线交替上升，不能说明哪种亚格子模型的尾流预测能力更突出，其中尾流速度廓线在7D后均由原来的“倒钟形”发展成为近高斯分布。

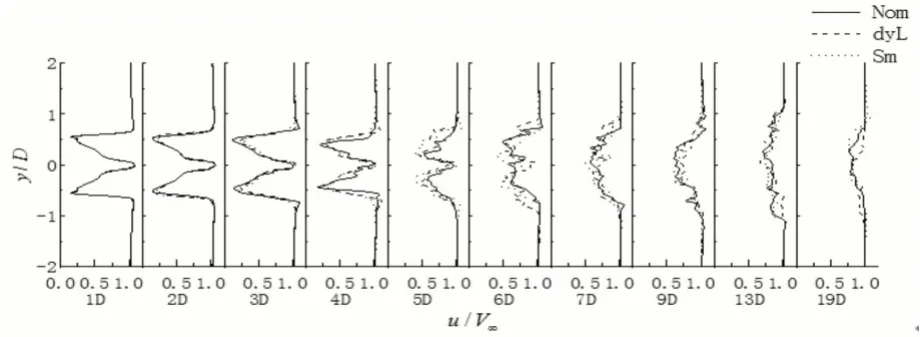
图3 使用dyL模型不同叶尖速比下风力机尾流时均轴向速度分布曲线Fig.3 Profiles of the Time Averaged Axial Velocity for Different Tip-Speed Ratios in dyL Model

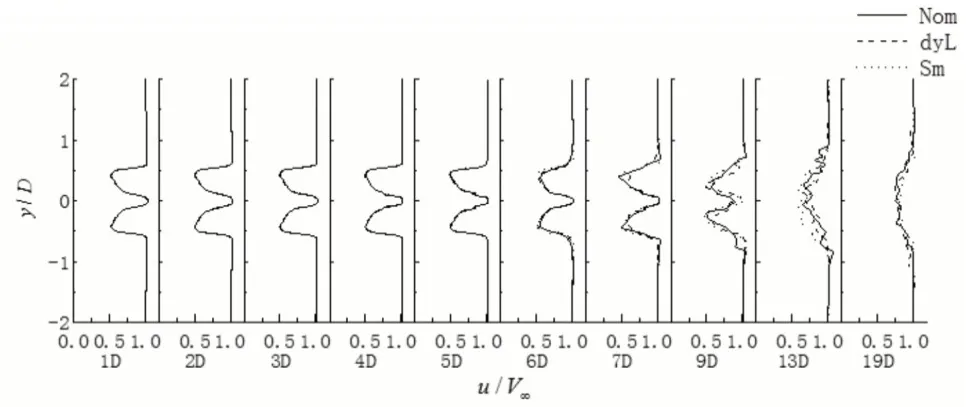
图4 λ=13.17时不同亚格子模型下风力机尾流均轴向速度分布曲线Fig.4 Profiles of the Time Averaged Axial Velocity for Different SGS Models in Tip-Speed Ratio of λ=13.17

为分析尾流场中湍流的流动特性，引入无量纲的雷诺应力与湍流切应力分别定义为，引入湍动能：

式中：u′、v′、w′-轴向脉动速度、横向脉动速度、垂向脉动速度。

对于Nom模型，νSGS=0，所预测的雷诺应力与湍流切应力为零，图5中不显示。λ=13.17工况下的风力机尾流中，雷诺应力与湍流切应力在叶尖涡与叶根涡区有明显的最大值与极大值；随着尾流向下游发展，尾流逐渐恢复，雷诺应力与湍流切应力逐渐变小；湍动能与雷诺应力的变化趋势一致，说明尾流场中正应力对湍动能的贡献最大，含有更多的能量；在近尾流区，由dyL模型产生的雷诺应力与湍流切应力大于Sm模型产生的雷诺应力与湍流切应力，随尾流发展两模型产生的应力趋于接近，表明尾迹随下游位置的变化呈现出逐渐增大的各向同性。比较图4～图6，在13D处，雷诺应力与切应力接近于零，平均速度亏损比产生的湍流更持久。

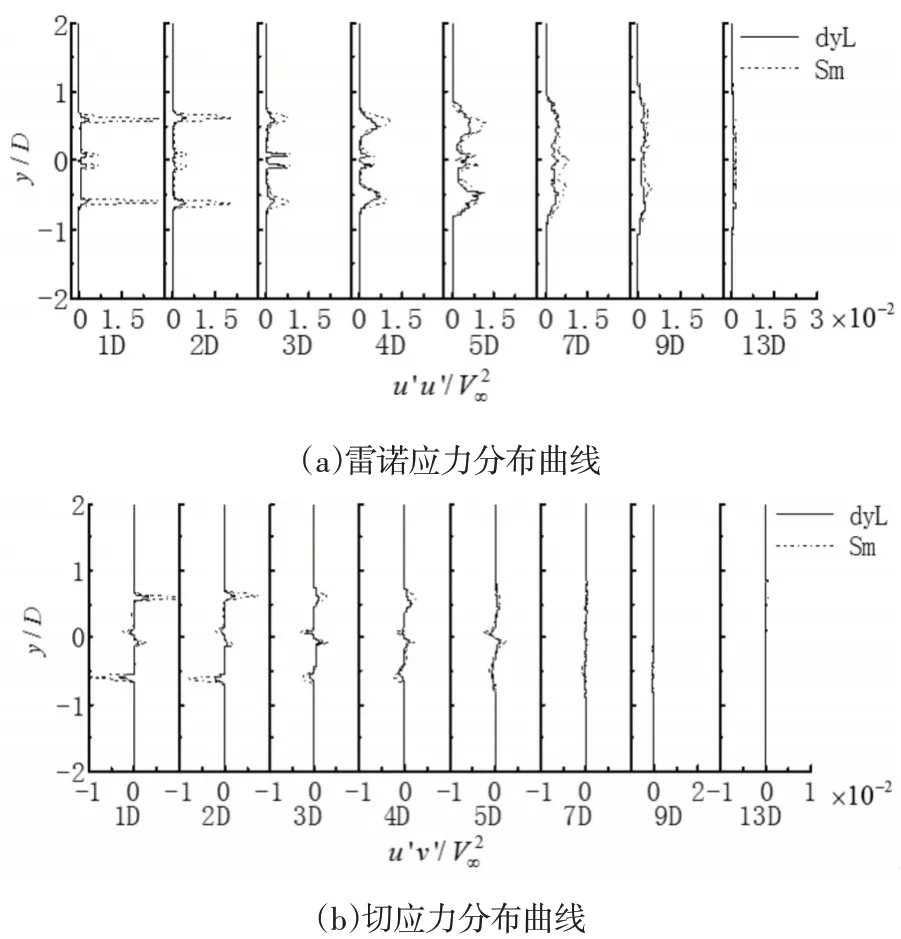
图5 叶尖速比λ=13.17时不同亚格子模型风力机尾流的雷诺应力（5a）切应力（5b）分布曲线Fig.5 Profiles of the Reynolds Stress（5a）and Shear Stress（5b）for Different SGS Models in Tip Velocity Ratio of λ=13.17

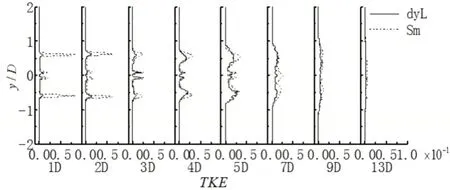
图6 λ=13.17时不同亚格子模型风力机尾流湍动能分布曲线Fig.6 Profiles of the TKE for Different SGS Models in Tip Velocity Ratio of λ=13.17

4.3 轴向速度干扰因子与速度环量

如图7所示，为轴向速度干扰因子ax=1-Vx/V∞沿叶片径向的时均分布曲线。由图可知，叶尖速比l=13.17时轴向干扰因子从叶尖到叶根增大过快，在0.85R处过大，其值接近0.5，此处的速度环量也最大，此时流动处于湍流状态，处理此问题通过传统的BEM理论无法解决，只能通过经验进行修正；l=8.23时，在0.2R～0.9R的叶片重载区，轴向干扰因子增长缓慢；l=5.98时，相比于大叶尖速比工况，ax变化范围最小。

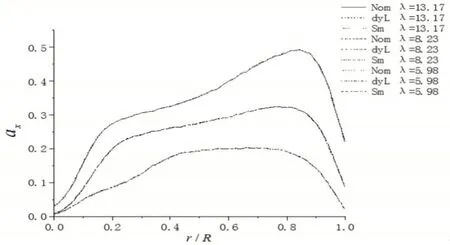
图7 轴向干扰因子沿叶片的径向分布Fig.7 Radial Distribution of the Axial Interference Factor along the Blades

如图8所示，为环量Γ=L/（ρ/Vrel）沿叶片径向的时均分布。图中，l=13.17时叶尖与叶根部分存在较大速度梯度，对应风轮处则存在较强的叶尖涡与叶根涡；且λ=13.17、λ=8.23时叶片重载区的环量变化较小；λ=5.98时环量沿叶片展向不断变化，在叶片中部部分区域大于λ=8.23工况，反映到风轮上表示两种工况下叶片推动风轮旋转的主要升力贡献区域发生变化，相比λ=13.17工况，叶尖涡与叶根涡强度较弱。使用三种亚格子模型所得到的轴向干扰因子与环量沿叶片径向的分布几乎相同，在叶片重载区有微小波动，且与λ=8.23、λ=5.98工况下得到的结论一致。

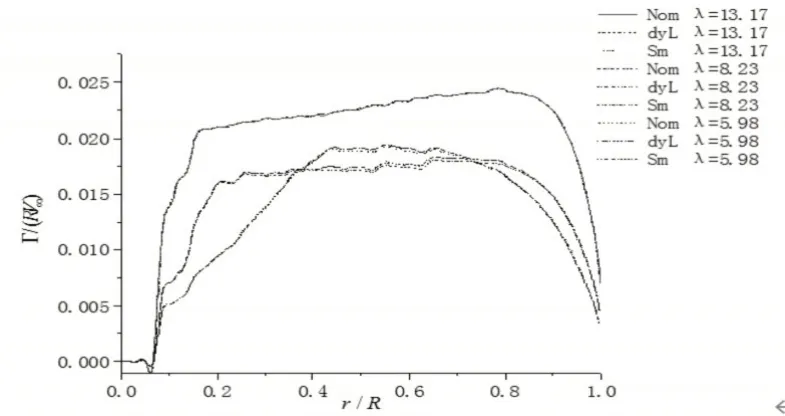
图8 环量沿叶片的径向分布Fig.8 Radial Distribution of Circulation along the Blades

4.4 尾涡分布

使用三种亚格子模型均能很好地获得风力机尾流场结构。如图9所示，为使用Q准则所得使用dyL模型在λ=13.17工况下风力机速度梯度第二不变量的不同Q值三维等值面，由图可知随着Q值增大，尾涡的圆柱形膨胀区直径逐渐变小，位于尾涡内部的高涡量层仍然能够被很好地捕捉，但风力机下游强度较弱的涡旋逐渐消失；相同位置处的尾涡由不同强度的涡旋组成，强度高的涡旋其对应的涡管直径较小，尾涡膨胀之前能量较高，能量较小的涡旋是尾涡组成中的主要部分。

图9 λ=13.17时使用dyL模型尾流不同Q值三维等值面Fig.9 3D Snapshots of Q Using dyL Models in λ=13.17

由曲线围成的闭环不规则图形（Q值二维等值面，图10）代表三维Q值等值面与Y-Z面的交线，其物理意义为涡量的模，适合提取边界层之外的涡结构；在远尾流区，根据其统计特性可以获得尾涡中各涡旋的大小与涡流间隙。

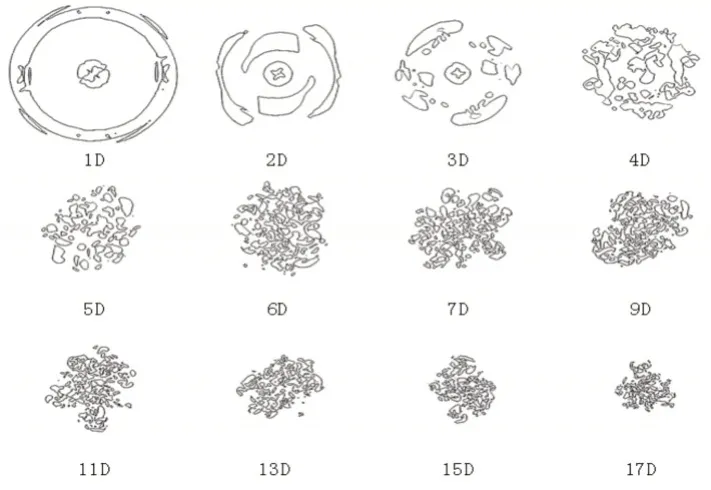
图10 使用dyL模型在λ=13.17工况下风力机尾流不同位置处的速度梯度第二不变量Q值二维等值面（Q=0.005）Fig.10 2D Snapshots of Q at Different Downstream Positions Using dyL Models in l=13.17（Q=0.005）

尾流从叶尖涡与叶根涡向下游传播，由图10可知在3D后尾涡开始溃散，不同Y-Z截面处的二维Q值等值面在均匀流下可视为近似圆形，随尾流位置的变化，圆的直径不断变小，说明尾流发展的过程中，强度较大的涡集中在尾涡中心，强度较小的涡在尾涡外围分布；若风力机在无限长区域内运行，随着尾流逐渐恢复，尾流中的湍流将逐步转化为入流状态的均匀流，不同强度的涡将逐渐消失。

5 结论

（1）雷诺应力与湍流切应力在叶尖涡与叶根涡区有明显的最大值与极大值，且由Lagrangian动力亚格子模型比Smagorinsky模型预测的应力大，随着尾流向下游发展，雷诺应力与湍流切应力逐渐变小，尾迹随下游位置的变化呈现出逐渐增大的各向同性；湍动能中正应力的贡献最大；在均匀入流条件下，平均速度亏损比产生的湍流更持久。

（2）相同位置处的尾涡由不同强度的涡旋组成，能量较小的涡旋是尾涡组成中的主要部分。尾流发展的过程中，强度较大的涡集中在尾涡中心，强度较小的涡在尾涡外围分布。

（3）对于所使用的三种亚格子模型，能预测出相似的尾流效应，亚格子模型的选择对尾流的模拟影响较小；νSGS=0时，求解过程只有数值耗散，仍能获得很好的模拟结果。