带有执行器失效的确定时间事件触发机制
2021-10-20黄堃锋洪嘉纯吴宇深朱厚耀
黄堃锋,洪嘉纯,吴宇深,朱厚耀
(广州大学机械与电气工程学院,广州 510006)
0 引言
随着互联网和通信技术的高速发展,网络控制系统(NCS)在实践中得到广泛应用,如智能建筑[1]、工业控制[2]、卫星通信[3]、交通网络[4]、无人机[5]等。
在实际的NCS 中,执行器和控制器之间的传输是通过对共享通信系统进行采样来实现的。但通信信道的带宽有限且不能在短时间内增加,而传统的时间触发系统状态采样和控制器更新是定期执行的,这将导致传统时间触发控制系统中通信资源的浪费[6]。在事件触发策略中,当系统状态满足预期事件条件时才会执行采样[7]。因此,为了节省网络带宽并最大限度利用通信资源,在控制系统中使用事件触发式采样代替时间触发式采样[8]。文献[9]提出了一种基于事件的线性系统在随机扰动下的控制策略;此外,由于实际操作中存在未知的干扰,对基于事件触发的不确定非线性系统进行了研究。文献[10]将一种新的分散事件触发控制方案应用于具有耦合时滞的复杂动力学网络,并设计了一种改进的事件触发控制器。
另外,控制的有效性取决于主动控制系统中制动器的操作是否正常,但在工业系统的实际操作过程中,执行器可能会以未知的形式发生故障,如果没有及时采取适当的补救措施,轻微的故障会降低控制性能,严重时可能导致控制系统崩溃[11]。因此,针对具有执行器故障的非线性系统,相关学者提出了许多基于非线性控制理论的故障补偿控制方法。文献[12]针对多输入多输出(MIMO)非线性系统不确定参数存在未知的时滞有界时变自适应控制问题,提出了一种新的反馈容错方案;文献[13]将自适应模糊输出反馈控制应用于随机非线性系统。上述控制方法有效解决了部分执行器故障问题,但执行器故障会影响控制精度,为避免较大的实际损失,如何快速补偿执行器故障值得关注。
在实践中,神经网络系统和模糊逻辑理论被用于处理自适应智能逼近跟踪控制问题[14]。文献[15]提出了神经网络的标准类别并研究了这些神经系统的全局渐近稳定性,有效解决了复杂非线性系统的跟踪控制问题。
上面提到的大多数控制方法都将李雅普诺夫稳定性归于渐近稳定性领域,在这种情况下,时间趋于无穷大时系统状态会收敛到平衡点。但是,随着控制系统越来越复杂、要求越来越高,需要无限时间的渐近收敛不能满足系统运行的需要,因此,提出了各种有限时间控制策略来解决非线性不确定系统的有限时间跟踪控制问题[16]。文献[17]考虑到给定的暂态性能指标,提出了一种自适应的有限时间控制方法来稳定非线性不确定系统。考虑到未知的扰动和执行器故障,文献[18]提出了一种新的自适应有限时间控制方法来分析随机非线性系统的稳定性。上述文献从定理的角度证明了它们可以达到有限时间的稳定性。为了克服实际情况中的未知干扰,文献[19]引入了自适应神经网络的非奇异滑动模式,确保闭环系统的有限时间收敛。
以上有限时间控制方法可确保系统状态在有限时间内收敛,但这些有限时间控制方法的收敛时间受未知的干扰影响,不能预先指定或设计。这意味着具体的稳定时间是未知的,所谓的有限时间只是估计的稳定时间的上限,而不是实际的收敛时间。因此,如何设计出具有预设收敛时间的有限时间控制器值得关注。在文献[20]中,常规的有限时间控制建立在一个新颖的缩放函数上,从而产生了可预测的收敛时间。但当执行器出现故障时,在规定的稳定时间控制框架内快速补偿故障并预设收敛时间仍是一个挑战。
基于上述讨论和反步设计法,针对具有不确定执行器故障的非线性系统,本文提出了一种事件触发的规定建立时间共识自适应补偿控制方法,主要内容如下。
(1)基于反步技术,提出一种不确定非线性系统的事件触发式有限时间自适应控制策略,该策略可以快速弥补故障并有效节省网络带宽。
(2)利用故障补偿策略,提出一种自适应神经网络控制方法来处理系统中未知的非线性项,可以保证系统状态的稳定性以及有限时间内的全局有界收敛。
(3)引入非线性变换函数,以确保跟踪误差在规定的建立时间内收敛到预定义的时间间隔内,并且变换后的系统依旧是稳定的,确保实际跟踪误差的有限时间收敛和规定的建立时间可以被调整;同时,可以统一预设有限收敛时间。
1 问题描述
1.1 模型和定义
考虑以下几类不确定的非线性系统

式中:xi∈R(i= 1,2,…,n)为系统状态;uj(t) ∈R(j= 1,2,…,m)为系统输入;y∈R 为系统输出;τj(x) ∈R为系统中已知的光滑非线性函数;fi(⋅) ∈R为系统中不确定的非线性函数;xˉi=[x1,x2,…,xi]T∈Ri;kj∈R为已知方向、未知大小的参数。
然后,考虑第j个执行器可能在运行期间失效,因此,在tr时刻的瞬时故障模型可以表示为
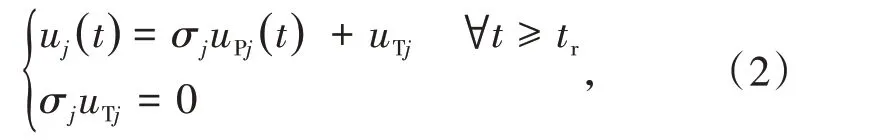
式中:uPj(t) 为系统的输入;0 ≤σj<1,tr和uTj均为不确定的常数。
本文考虑以下2 种程度的执行器失效:一是执行器部分失效,这就意味着执行器输出uj(t)在运行时失去了一些性能,因此就有uj(t)=σjuPj(t) 和0 <σj<1;另一个是执行器完全失效,这就意味着执行器输出uj(t)不再受uPj(t) 的影响,但受uTj的影响,所以就有uj(t)=uTj和σj= 0。
因此,可实现以下带有执行器失效的系统模型
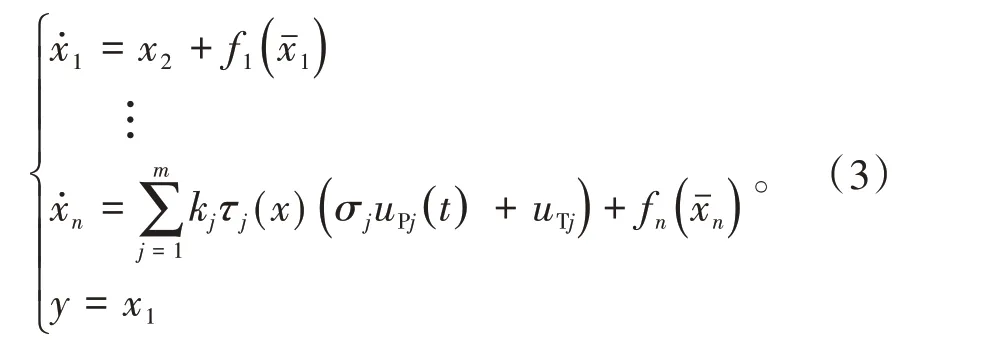
1.2 事件触发控制设计
由于通信网络的网络资源有限,为了节省包括通信信道带宽和计算能力在内的网络资源,可以考虑采用以下事件触发方案

式中:tp(p∈R+)为控制器的更新时间;ωj(t)为要设计的触发机制的函数;e(t) =ωj(t)−uPj(t)为测量误差;F(uPj(t))为待设函数。
1.3 转换函数概述
为了达到实际规定的建立时间跟踪性能,可以引入以下转换函数

(2)为了确保变量在转换前后具有相同的初始值,它满足c(0)= 1。
(3)c(t)是有界且可微的,同时ċ(t)是有界的,这就意味着|ċ(t)|≤cmax,其中,cmax>0且cmax为常数。
(4)在自适应控制方案的设计中,使用神经网络近似未知的非线性函数。 明确φ(x)=[φ1(x),φ2(x),…,φn(x)]T为已知的基函数向量,η=[η1,η2,…,ηn]T为权重向量。
1.4 近似函数的研究
在自适应控制方法的设计中,径向基函数神经网络(RBFNNs)用于近似未知的非线性函数,因此,对于未知的连续非线性函数f(Y),可以在紧凑集上近似

式中:φ(Y)=[φ1(Y),φ2(Y),…,φD(Y)]T为已知的基函数向量;D为神经元的数量;η=[η1,η2,…ηD]T∈RD为最佳权重向量;ρ>0 为近似误差。
然后,高斯函数φi(Y)满足
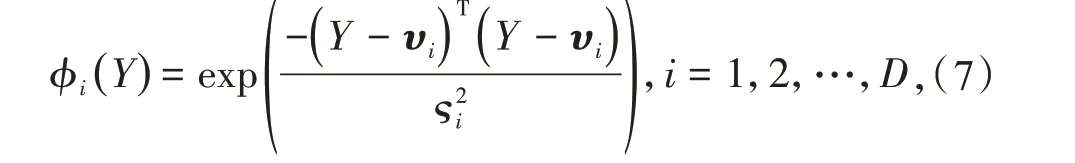
式中:D为神经网络(NN)节点的编号,D>1;υi=[υi1,υi2,…,υiM]T为高斯函数的中心;ςi为高斯函数的宽度。
为了促进自适应控制器的设计和得到合适的自适应控制器,提出了以下假设。
假设1[21]:在时间间隔[Tq,Tq+1)(q=0,1,…,F)中设定M代表执行器全部失效,设定MPj代表其他没有全部失效的执行器,明确MPj∪M={1,2,…,m};F为自然数。
假设2[21]:全部失效执行器的最大数量为m−1,但部分失效执行器的数量最多可达m,剩余的驱动力便可以达到控制目的;同时,任何执行器都不能多次切换状态。
设定T0= 0,假设在时间间隔[Tq,Tq+1)(q= 0,1,…,F)中共有mj(0 ≤mj≤m)个执行器失效且没有出现新的执行器失效。显然,在时间间隔[T0,T1)中所有执行器都可以正常工作,新的执行器失效会出现在T1时刻之后。从假设2中可得,TF是有限的,TF+1是无限的。
假设3:r是有界且已知的期望信号;此外,r具有(n+ 1)阶导数。
2 控制器设计
2.1 系统模型分析
为了补偿执行器失效,设计了基于相对阈值策略的事件触发的自适应补偿控制器。值得一提的是,自适应补偿控制方法采用反步技术来跟踪测量中的未知参数,其中设计n个递归步骤,具体计划如下。
引入以下虚拟误差方程式

式 中:αi−1(i= 2,3,⋅⋅⋅,n) 为 虚 拟 控 制 律;zi(i=1,2,⋅⋅⋅,n)为可变误差。
为了实现自适应和在规定的稳定时间内的实际跟踪,引入非线性转换函数c(t)来改变实际跟踪误差和虚拟误差,转化后的实际跟踪误差e和虚拟误差zi可以定义为

2.2 自适应事件触发控制设计
在系统执行器部分失效的情况下,可以通过更大的阈值获得更长的更新间隔。当系统状态趋于稳定时,可以通过较小的阈值获得较短的更新间隔,然后通过一个更精确的控制信号uPj(t)获得更好的系统性能。因此,可以设计用于补偿由触发机制引起的测量误差的控制器,建立以下事件触发策略。


式中:γj为正定矩阵。
2.3 稳定性分析
考虑带有执行器失效的系统(3),虚拟控制器(10),(12),自适应律(11),(13),参数更新律(16)以及事件触发的规定的稳定时间共识控制器(14),可以保证以下结果[22]。
(1)所考虑系统的所有信号都是有界的。
(2)存在一段时间t∗>0,这样,执行间隔t∗≤{tk+1−tk}都小于有界t∗,∀k∈z+,因此可以避免芝诺行为。
首先,选择李雅普诺夫函数Vn为
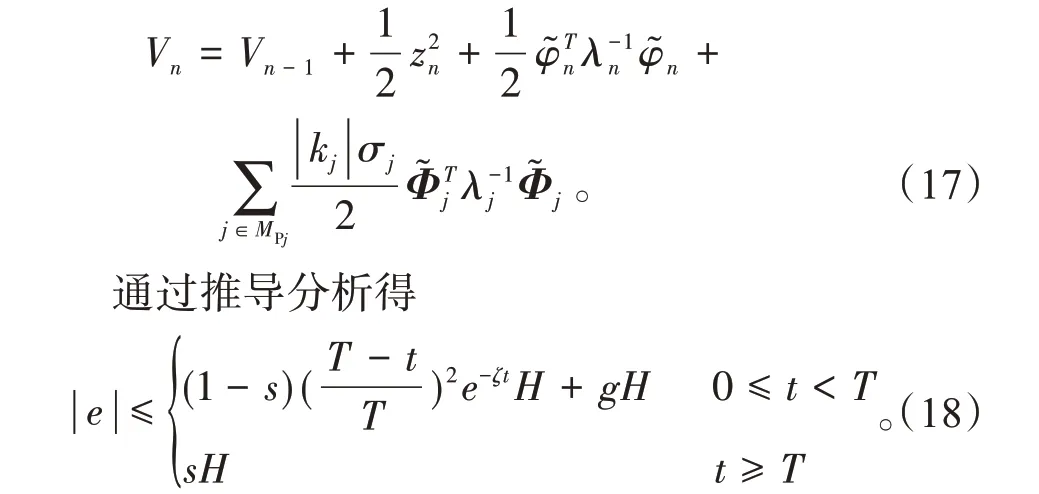

通过分析规定的建立时间T可知,通过调整T,ζ和s,可以影响系统的跟踪误差和收敛速度。
3 仿真分析
通过实例仿真验证所提出的方案是否适用于带有执行器故障补偿的不确定非线性系统。
考虑一种单连杆机械臂模型
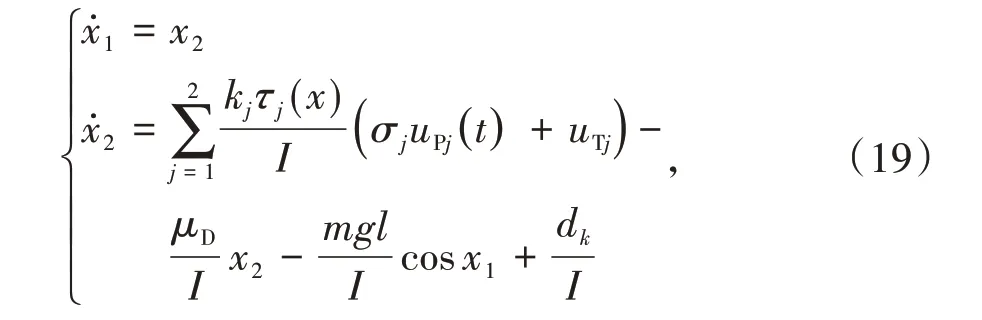
式中:x1,x2分别为位移和速度;I为惯性;m为质量;g为重力加速度;l为质心到关节的长度;μD为黏性摩擦系数;设置障碍为dk= sint。
系统参数如下:已知和未知函数分别为f1(xˉ1)=x1(1 −sin2x1)+ 0.1cosx1和f2(xˉ2)= −3.5x2+x1x22+0.1sin(2x1x2);kj= 1;函 数τj(x) = 2.4 + 0.1sinx1(j=1,2);参考输出信号为r= sint。

假设单连杆机械臂的执行器1 在5 s 后发生部分失效,10 s 后完全失效,执行器2 运行正常,其参数设置为:σ= 0.5(输入、输出比为50%)。系统输出和参考信号如图1 所示,不具有上述控制方法的控制输入如图2 所示,具有事件触发的控制输入如图3 所示,系统的跟踪误差如图4 所示,事件触发量及其间隔如图5所示。
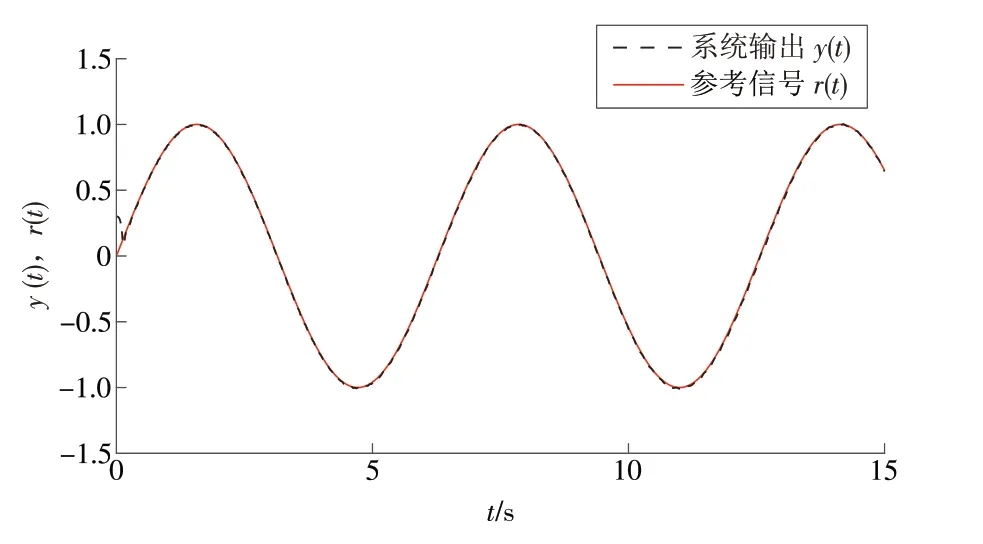
图1 系统输出和参考信号Fig.1 System output and reference output
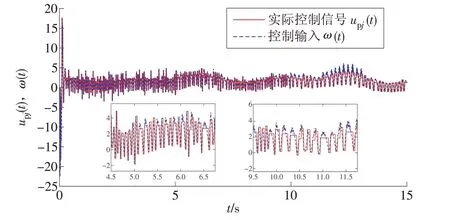
图2 不具有控制方法的控制输入Fig.2 Control inputs with no control methods

图3 具有事件触发的控制输入Fig.3 Event-triggered control inputs
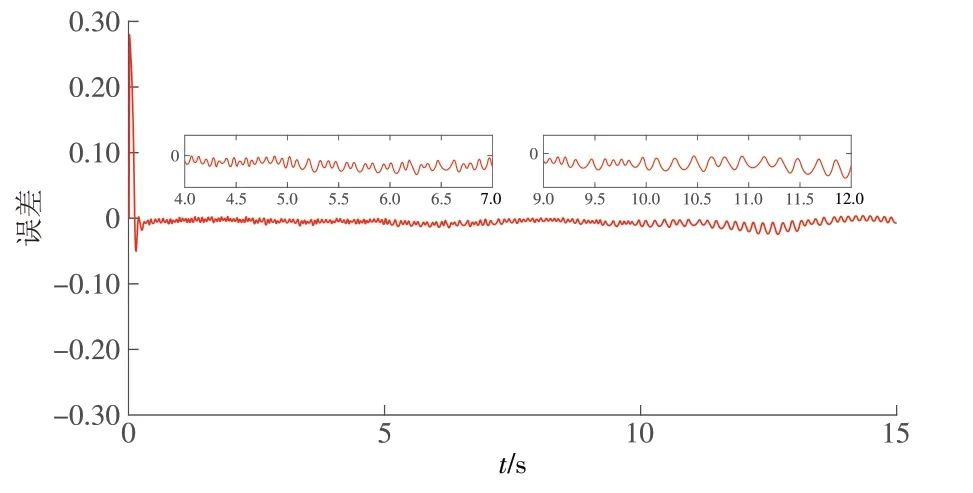
图4 系统跟踪误差Fig.4 Tracking error of the system
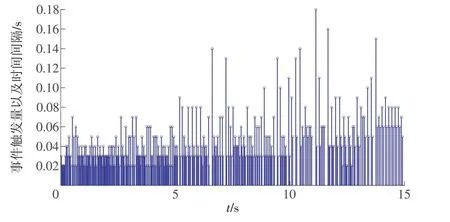
图5 事件触发时间间隔Fig.5 Inter-execution intervals
仿真结果表明:单连杆机械臂的执行器1 在5 s后发生50%的故障,输入输出比为50%,10 s 后完全失效,预设稳定时间为0.4 s。从图1 可以看出,执行器2 正常工作的情况下,本文提出的方法确保了单连杆机械臂的跟踪控制,并且系统的所有信号都是有界的。从图2 可以看出,没有加入控制方法的执行器1 在5 s 后发生部分失效的情况下系统状态受到了很大的影响,在10 s 后完全失效的情况下进入了卡死状态,输出不再受输入的影响。从图3可以看出,采用本文提出的控制方法,与执行器正常运行时相比,执行器1 在5 s 后发生部分失效的情况下系统波动幅度较小,在10 s 后完全失效的情况下受到了一定的影响。图4 的结果显示,跟踪误差在5 s后出现了轻微的波动,10 s后出现了较大的波动,但波动范围在预期误差范围内,系统在0.2 s 后误差就稳定在了5%内,证明系统在设定的时间0.4 s内达到了预设目标状态。
从图5可统计得出触发量数据,见表1。

表1 触发量数据Tab.1 Number of trigger
从图5 可以看出,该方法最少可节省带宽0.02 s,最多可节省0.18 s。结合表1中的触发量数据,执行器1在5 s后发生部分失效,10 s后完全失效,执行器2 正常运行的情况下,在每2 s 的时间间隔内,触发事件的数量随控制输出的变化而变化,以减少带宽资源的消耗。在传统的时间触发中,每2 s的触发次数为200,而在本文涉及事件触发中,每2 s 的平均触发次数为46,相比之下,带宽资源节省率达77%。
4 结束语
本文针对具有执行器故障的不确定非线性系统,提出了一种基于事件触发的规定建立时间共识自适应补偿控制方法。为了有效节省网络带宽,通过反推技术,提出了一种事件触发的有限时间补偿控制策略;同时,对于具有执行器故障的不确定非线性系统,设计了一种有限时间自适应补偿控制器,该控制器可以确保发生故障时系统状态快速收敛。引入非线性变换函数以确保跟踪误差在规定的建立时间内收敛到预定间隔;同时,提出了一种基于事件触发的规定建立时间共识自适应补偿控制方法,该方法可以统一预设有限时间,并且系统在有限时间内收敛。仿真结果表明,该方法可以保证系统的跟踪性能,实现系统状态的全局一致性和稳定性,同时避免了芝诺行为。
