基于客流的地铁网络节点重要度评价方法

2021-10-20徐敏

山东交通学院学报 2021年4期

徐敏

重庆公共运输职业学院,重庆 402247

0 引言

从Watts[1]和Albert[2]分别于1998年和2000年提出小世界网络(网络结构中两节点之间的距离很小)和无标度网络(网络单个节点与其他节点的连接数量满足幂律分布)以来,掀起了人们对各种网络关键节点的研究热潮。近年来,随着轨道交通的迅猛发展,各大城市轨道交通线网规模越来越大,研究地铁线网中车站节点的重要度有助于人们对关键车站的安全监控和重点防范,有利于地铁系统的高效运营管理。

目前国内外主要对地铁网络重要节点的抗毁性、攻击策略、网络效率等方面进行评价研究。Angeloudis等[3]对地铁网络抗毁性进行研究,发现了地铁网络在蓄意攻击下整个网络的关键点;Kurant等[4]利用分层网络思想,建立基础设施网络和车流网络模型,分析攻击策略下的关键节点;刘志谦等[5]采用Space L方法研究攻击换乘站对广州轨道交通网络安全的全局效率及局部效率的影响度;叶青[6]以基于网络效率影响最大为关键点判定标准,用Space L法构建网络模型,研究蓄意攻击下重庆轨道交通网络最关键的2个节点;王班等[7]以自然连通度为测度指标对网络的抗毁性进行研究,提出提高抗毁性能的有效手段;杜斐等[8]采用网络全局效率为鲁棒性指标,用Space L模型对上海轨道交通网络进行仿真试验,研究网络站点的随机故障与蓄意攻击的抵抗性;李倩[9]研究级联失效情况下北京地铁网络中换乘站节点的重要度与其他线路重要度的变化。

城市轨道交通网络节点重要度的评价方法主要有topsis法、m阶邻接节点重要度评价法与统计法等[10]。薛锋等[11]基于复杂网络理论分析成都地铁拓扑特性,构建评价指标体系,运用topsis方法完成节点排序,仿真并验证得到节点的重要度;张晋等[12]分别构建Space L和Space P拓扑结构模型,运用统计方法对北京地铁网络进行分析,检验网络符合小世界和无标度网络特征,而且存在少量关键节点;孙立山等[13]运用客流传播和网络效率模型,考虑车站功能减弱和中断情况下的网络稳定性变化,研究北京地铁的关键点和薄弱环节;谌微微等[14]构建二阶张量模型,统计重庆轨道交通网络特征指标,用3个中心指标评价节点的重要度,指出重庆轨道交通网络的4个关键站点;卢祝清等[15]利用复杂网络理论计算武汉地铁线网的特征值并作为评价指标,确定关键车站和区间,对比分析优化结构与单纯追求网络效率的重要性;许海霖等[16]设计并优化了topsis方法,对北京地铁网络节点进行重要性评价;刘杰[17]在分析轨道交通网络和功能的基础上,建立包含基础设施、客流和车流的分层网络模型,以网络全局效率为测度目标,研究地铁网络抗毁性能的变化,结果表明广州地铁存在4%的关键节点;胡映月等[18]结合真实客流、线路运输能力以及线网结构3方面指标识别关键站点,结果发现客流负荷强度大的车站更易受大客流冲击。

已有研究多集中在地铁网络物理拓扑结构上,没有考虑客流因素的影响,如文献[18]考虑了客流对地铁线网的冲击影响,但没有考虑节点重要度和时间尺度的关系。客流的收集是有时间间隔的,以“小时”为单位统计客流和以“天”为单位统计客流,得出的结果不同。本文充分考虑网络客流和时间尺度因素,提出基于客流的地铁网络节点的重要度评价方法,并通过实际案例计算和仿真验证评价方法的合理性。

1 网络模型

以成都地铁为研究对象,目前成都地铁开通运营1#、2#、3#、4#、7#和10#共6条线路,合计156个车站,将整个成都地铁车站抽象为节点,车站之间直接相连的线路抽象为边,构建物理网络模型

G1=(V,E1),

(1)

式(1)属于有向无权重图模型,其拓扑结构如图1如示(其中红色节点表示换乘车站,黑色节点表示一般车站)。

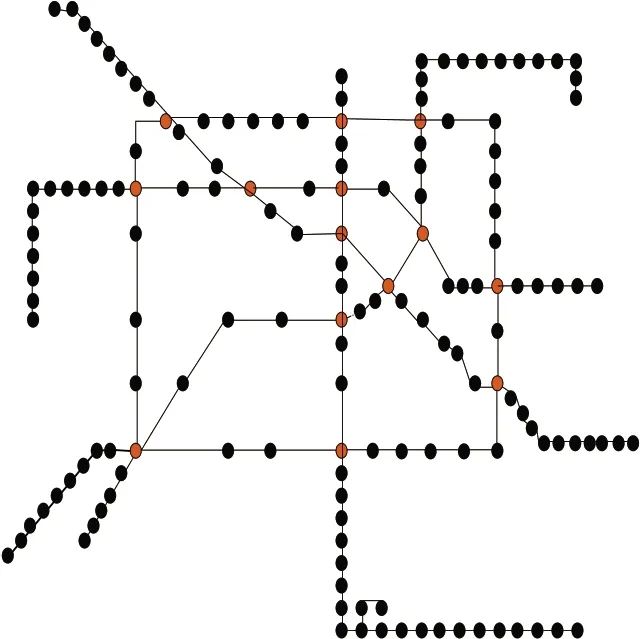
图1 成都地铁拓扑结构

考虑客流的影响,以“天”为单位收集成都地铁2019-09-01—09-30(时间T=30 d)的OD(O为始发站,D为目的站)客流数据,在此基础上构建客流网络模型

G2=(V,E2),

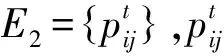
限于篇幅这里只给出2019-09-01—09-04的OD客流网络结构图,如图2所示[19]。

图2中线条的不同颜色和粗细表示不同的客流权重,从图2可看出:客流物理网络几乎是一个全连通有向加权网络,随着每天出行目的与出行时间等方面的差异性,在物理网络不变的情况下,客流结构的有向权重是变化的,即任意不同车站之间都有客流产生,且每天客流权重分布不同[20]。节点重要度由物理网络和客流网络共同决定,所以网络节点的重要度每天都随客流分布的变化而变化[21]。

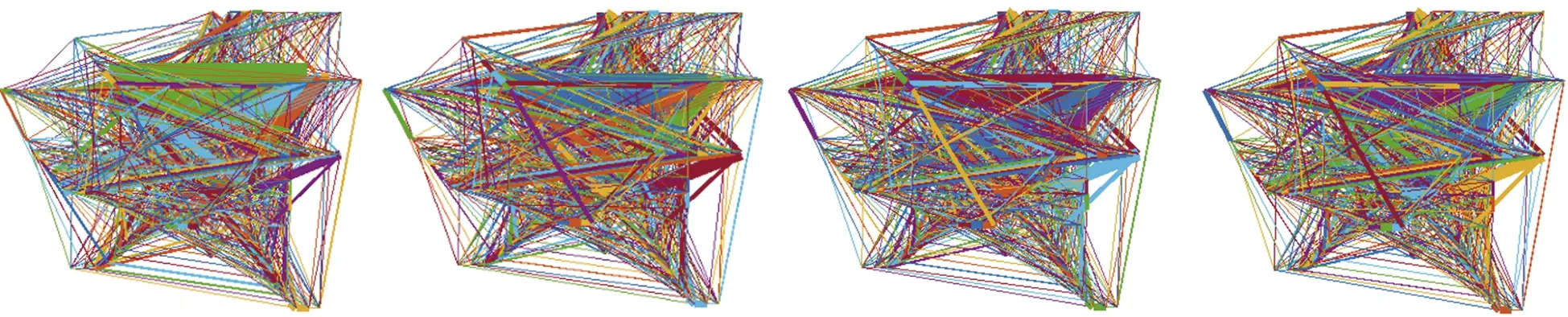
a)2019-09-01 b)2019-09-02 c)2019-09-03 d)2019-09-04 图2 不同日期的OD客流网络结构

2 节点重要度评价算法

2.1 节点重要度定义

在站点的网络结构中,任意2个节点之间都存在OD客流,当某节点在路网中消失后,会存在路网其他节点到该节点的客流失效,以及从该节点出发到其他节点的所有客流也将失效,将节点失效后发生的客流损失量定义为损失客流[22]。

损失客流占路网总客流的比例随每天客流总量的变化发生变化,该节点的重要程度也发生相应改变。

将i节点的重要度定义为第t天第i节点失效后,给客流网络造成的客流损失数量占当天客流总量的比例,则有[23]

(2)

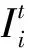
2.2 节点重要度评价算法

由式(2)可以看出:

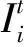
设某地铁网络共有N个节点,即网络节点关联性矩阵为A=[aij]N×N,计算节点的重要度[24]。

1)初始化时间,设t=1。

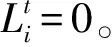
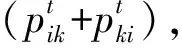
4)因为i节点失效导致j和h之间无连通路径,利用图论算法判断Ai的连通性,对于任意节点j、h,j∈V,h∈V,且j≠h≠i,得到连通性矩阵

C=[chj]N×N,

式中:chj为h到j节点的连通性值,chj=0表示节点h、j之间无连通路径,chj=1表示h、j之间至少存在一条连通路径。

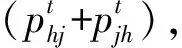
(3)

将式(3)带入式(2),计算得到第1天第1节点的重要度I11。

6)令i=2,将无站点失效的初始关联矩阵重新赋值给A,即A=A′,转步骤3)。直到当i=N时,分别得到I21、I31、…、IN1。

7)当i>N时,则令t=2,转步骤1),开始计算第2天i节点的重要度。分别得到I12、I22、I32、…、IN2。直至当t>T时(T为总时间),算法结束。

最终节点i的重要度Ii取所有时间点上的平均值,即

(4)

3 实例分析与仿真验证

3.1 实例分析

按上述算法计算得到成都地铁网络156个车站(节点)重要度的变化情况,如图3所示。

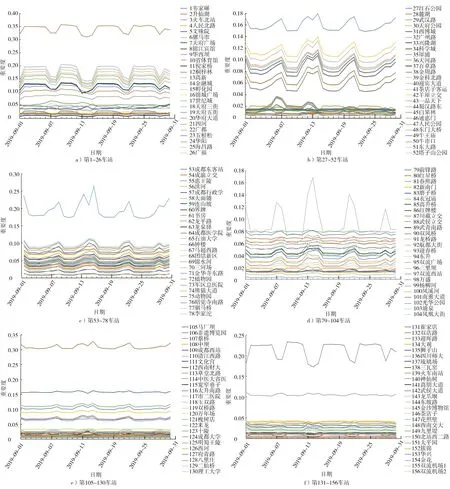
图3 成都地铁156个车站重要度随时间的变化情况

从图3可以看出:节点的重要度具有明显的层次性,不同节点的重要度都在各自水平上呈现周期性的波动,多数节点的重要度随时间尺度的变化相对稳定且波动不大。利用式(4)计算各节点最终的重要度,限于篇幅,仅列出排名前10个节点的计算结果,如表1所示。

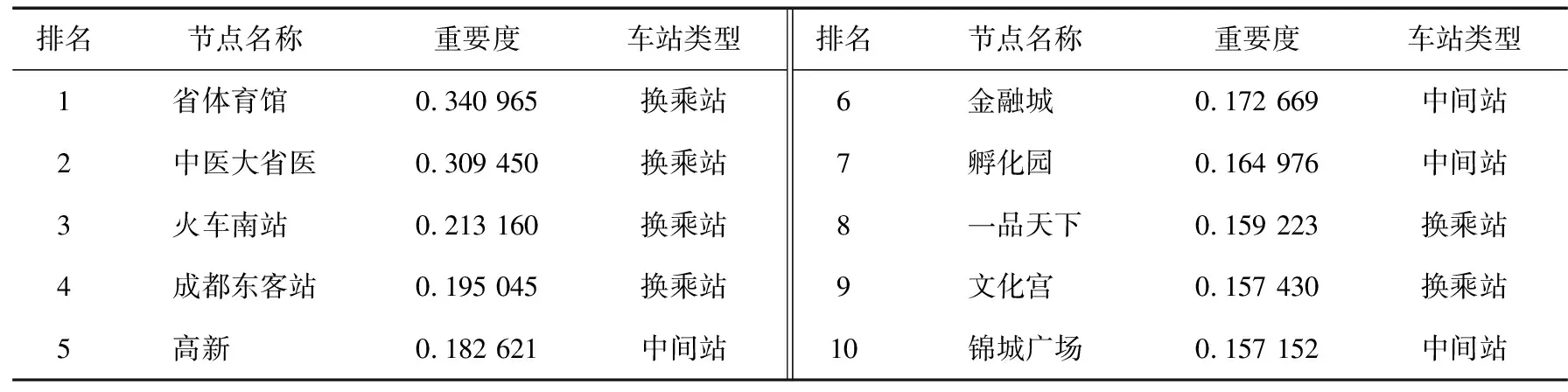
表1 重要度排名前10的节点情况

从表1可以看出:

1)重要度排名前10的节点中有6个换乘站,说明换乘站客流量较大,同时换乘站也是各线路保持连通性的关键节点。

2)表1中4个中间站是整个网络的关键节点。成都地铁换乘站共有14个,除表1中的6个,还有驷马桥、骡马市、火车北站、天府广场、市二医院、槐树店、春熙路和太平园8个换乘站,说明换乘站的重要度不一定都比中间站高,少数中间站也可能成为全局的关键节点。

3)高新、金融城、孵化园和锦城广场站为顺序相邻站,且都属于1#线的中间车站,说明在网络中除存在关键节点外,还存在重要区域(即由多个重要度较高的相邻车站组成)。对于这种由点到面的特性在运营管理中应予以高度重视。

3.2 结果验证

为了验证本文计算结果的有效性,采用目的攻击和随机攻击方法进行仿真试验,其中目的攻击以本文得到的节点重要度排名由高到低依次攻击使对应节点失效,随机攻击即随机选择节点攻击使其失效,以客流损失后剩余客流占总客流的比例为测度指标,得到的结果如图4所示[25]。

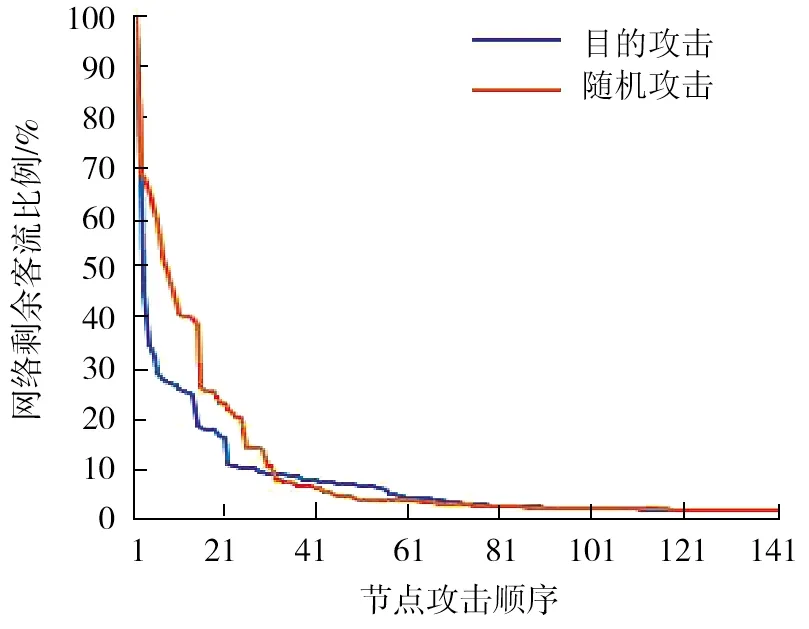
图4 目的攻击和随机攻击下测度指标的变化

由图4可以看出:在按节点重要度由高到低的目的攻击下,网络客流损失下降幅度和速度明显高于随机攻击,对排名前21的节点攻击完成后,剩余客流仅为总客流的10%,在21次攻击后目的攻击和随机攻击的效果基本一致,说明当网络中关键节点被攻击后网络指标已处于很低水平,剩下的节点造成的影响十分有限,说明对成都地铁网络关键车站的评价计算是有效的。