尼雅水库坝料动力特性研究及三维地震反应分析

何建新，王 景，杨海华

(1.新疆农业大学水利与土木工程学院，新疆 乌鲁木齐 830052；2.新疆水利工程安全与水灾害防治重点实验室，新疆 乌鲁木齐 830052)

新疆尼雅水库位于尼雅河中上游河段，大坝为碾压式沥青混凝土心墙坝，最大坝高131.8 m，具有防洪、灌溉、发电等综合利用功能，其安全稳定对社会发展至关重要。新疆地区地震频发，震源浅，强度大。因此，在尼雅大坝设计时采用“金包银”结构。典型设计断面图如图1所示，坝体外部采用堆石料填筑，内部采用砂砾料填筑，心墙两侧采用细级配的砂砾料充当过渡料进行填筑。筑坝材料的动力特性直接影响大坝的抗震性能，因此研究筑坝材料动力特性并对大坝进行动力分析计算。

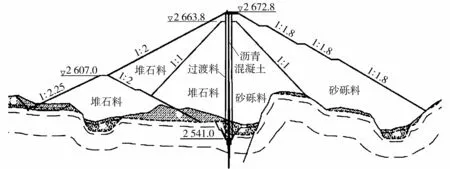
图1 尼雅水库大坝典型断面(单位：m)

我国已建和拟建的百米以上高土石坝近百座，且大多位于高地震烈度区，这些高坝一旦因地震失事，后果将是灾难性的，因此对高土石坝的地震安全应十分重视[1]。随着高土石坝建设的快速发展，坝料的动力特性成为岩土工程研究的重要课题之一。目前，已有学者对大坝地震安全的研究主要集中在坝料的动模量和阻尼比，以及材料本构模型方面，个别学者考虑了覆盖层的影响。凌华等[2]对筑坝堆石料进行了动力变形特性试验，分析了围压和固结比对最大动模量、动模量衰减规律和阻尼比的影响；杨杰等[3]基于量子遗传算法(QGA)和支持向量机(SVM)建立细观参数标定模型；沈珠江等[4]对吉林台面板坝两种堆石料进行动力试验，采用动应力-动应变骨干曲线为双曲线的假定，提出符合堆石料的动本构模型；朱晟等[5-6]通过复杂高应力条件下粗粒土动力试验，提出反映材料振动硬化特性的幂函数型动应力-应变关系模型和阻尼比计算公式，同时基于沥青混凝土的动三轴试验，建立计算模型，对沥青心墙坝进行动力分析；房恩泽等[7-8]研究了不同围压、孔隙比和固结比等对堆石料模量阻尼比特性的影响，并改进沈珠江模型的残余剪应变计算公式；邹德高等[9]对筑坝堆石料的动力残余变形特性进行研究，并对沈珠江模型进行了改进。本文基于室内动三轴试验，研究沥青混凝土心墙坝筑坝材料动力变形特性，并借助三维有限元进行动力分析，深入探讨坝体遭遇实际地震作用时的应力-应变关系及永久变形特性，进一步研究沥青混凝土心墙坝的抗震特性，试验结果可供大坝的结构稳定设计和安全施工参考。

1 坝料动模量和阻尼比试验

1.1 试验方法

采用WYS-2000大型多功能动静三轴试验机(图2)对坝料进行动力特性试验。该仪器主要技术参数如下：最大轴向静荷载2 000 kN；最大轴向动荷载1 000 kN；最大围压5.0 MPa；最大反压力2.0 MPa；最大轴向行程400 mm；动荷载频率0.01～10 Hz。试样尺寸为∅300 mm×700 mm。由于现场填筑的坝料最大直径为600 mm，依据GB/T 50123—2019《土工试验方法标准》，通过等量替代和相似级配的方法将坝料进行缩尺，以满足室内试验要求，试验级配曲线如图3所示。本次试验选取的固结应力比Kc分别为1.5和2.0，在围压分别为0.4 MPa、1.0 MPa和1.6 MPa下进行试验。

图2 WYS-2000大型多功能动静三轴试验机

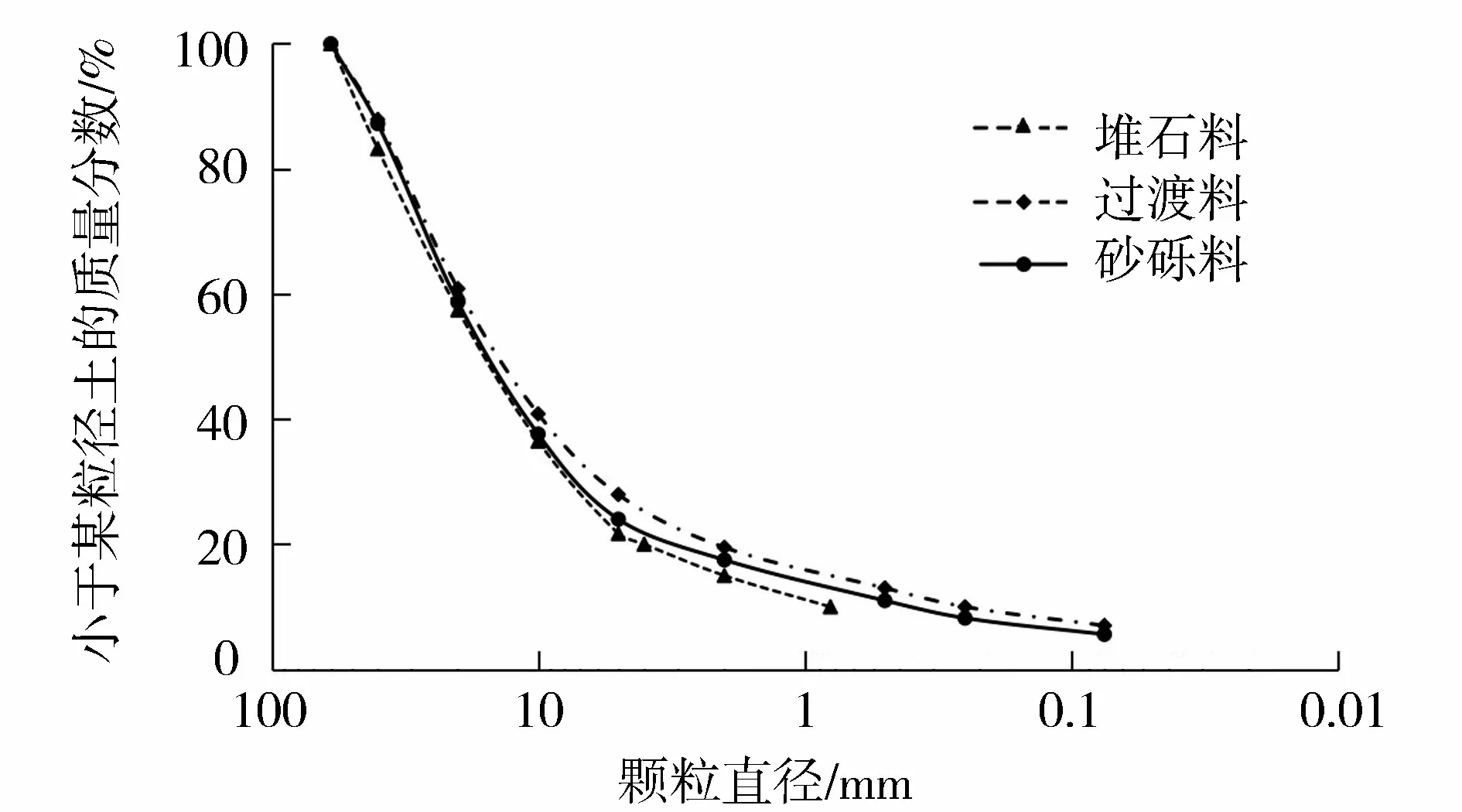
图3 试验级配曲线

1.2 结果与分析

根据等效线性黏-弹性模型[10](Hardin-Drenevich模型)，假定动荷载作用下应力-应变曲线为双曲线，对坝料试验结果进行分析。砂砾料、过渡料及堆石料动剪切模量Gd与动剪切应变关系曲线γd如图4所示。由图4可知，γd在10-4～10-2之间变化，Gd随着γd的增大而减小，且围压和固结比的变化对Gd影响较大。固结比相同时，围压越大，坝料在固结时被挤压越密实，坝料的Gd随着围压的增大而增大。围压相同时，固结比越大，试样中的土颗粒同样会被挤压密实，Gd增大。工程建设中的堆石料多为岩石风化或山体经爆破后得到的尖角料，固结时由于颗粒间的挤压和摩擦会产生颗粒破碎现象，从而使原级配发生改变。而砂砾料是经水流冲击搬运等作用形成的以圆形或亚圆形为主的级配料，颗粒强度较高。由试验结果可知砂砾料和过渡料的最大动剪切模量比堆石料高4%～11%，砂砾料和过渡料抵抗变形的能力优于堆石料。

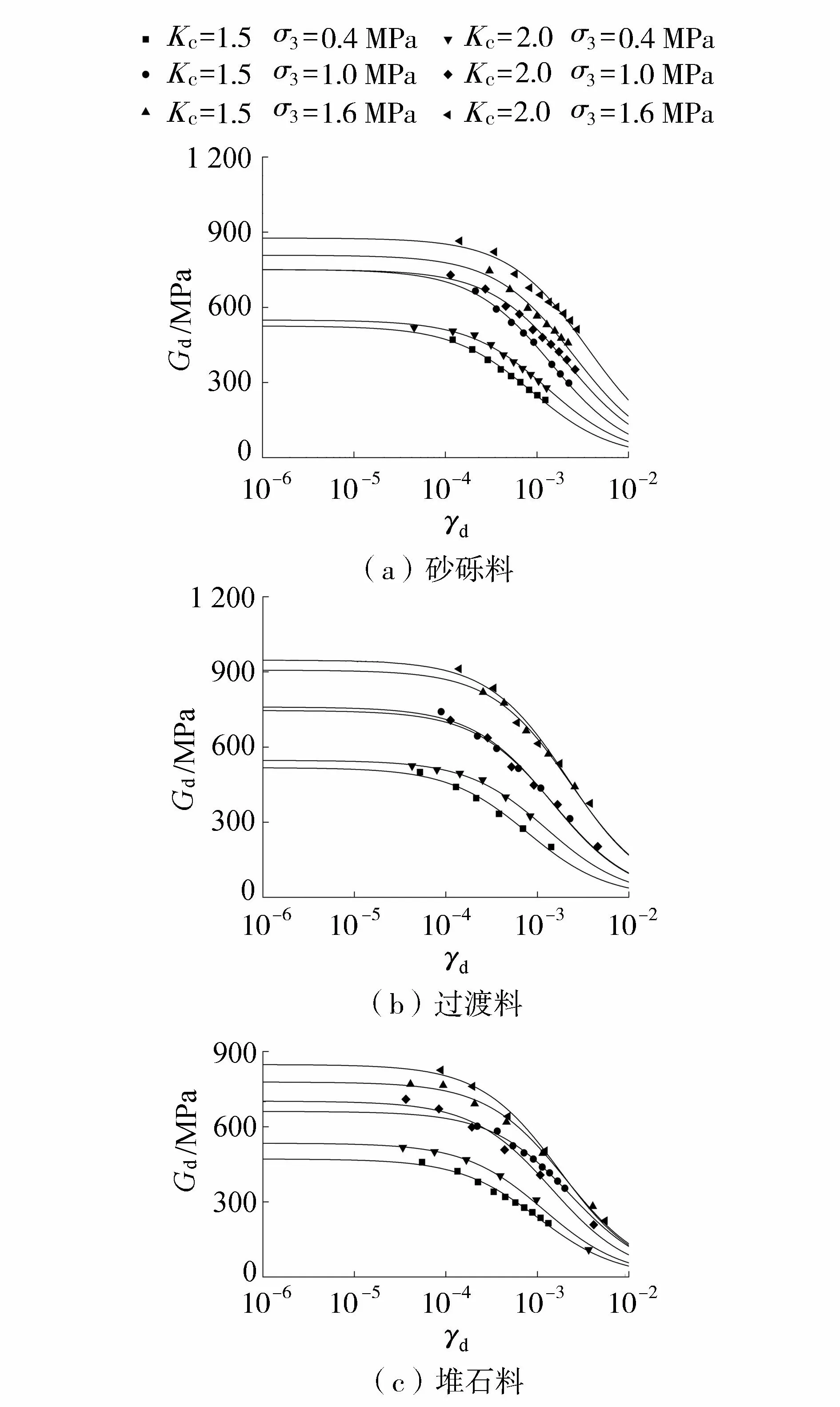
图4 不同固结比、围压下坝料Gd-γd关系曲线

Hardin等[10]认为阻尼比与动应变也呈双曲线关系。图5为Kc=1.5时不同围压下3种坝料λ-γd关系曲线，由图5可知，围压对坝料阻尼比的影响较大，3种坝料的阻尼比均随着围压的增大而减小，且随着围压的增大，坝料阻尼比的增长越缓慢[11-14]。统计3种坝料在不同固结比作用下的最大阻尼比λdmax，如表1所示。由图5和表1可知，3种坝料的阻尼比随着动剪切应变的增大而增大，由于过渡料的细颗粒含量高于砂砾料中细颗粒含量，相同固结比作用下过渡料的最大阻尼比高于砂砾料。堆石料为岩体爆破级配料，颗粒表面以棱角形为主，受压后颗粒间发生错动摩擦使棱角破碎，导致原级配改变，且围压越大，颗粒破碎越明显，故堆石料的最大阻尼比比砂砾料和过渡料高4%～14%，堆石料吸收的应变能高于砂砾料和过渡料。根据设计，在外侧填筑堆石料有利于坝体适应变形和维持边坡稳定。

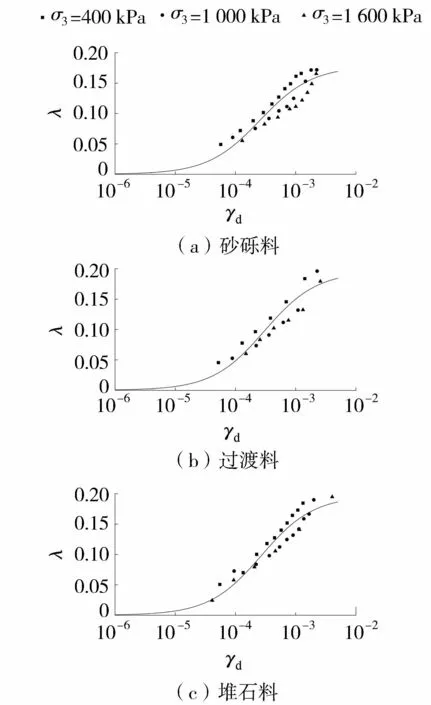
图5 不同围压下坝料λ-γd关系曲线(Kc=1.5)

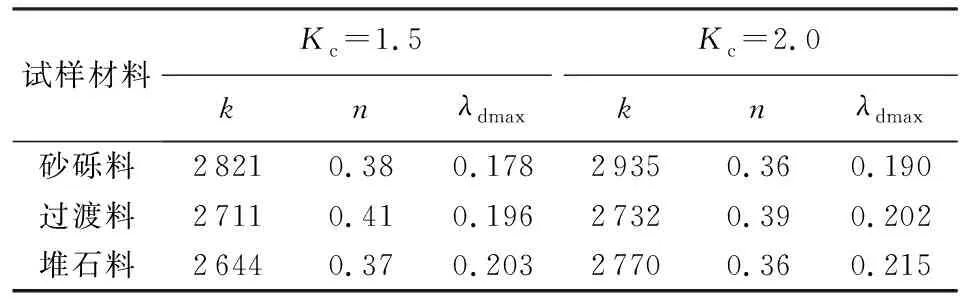
表1 动剪切模量系数、指数和最大阻尼比

根据动三轴试验得到归一化的动剪切模量Gd/Gdmax和等效阻尼比λ如表2、表3所示，可知动剪切模量和阻尼比具有良好的归一性，试验结果可靠。

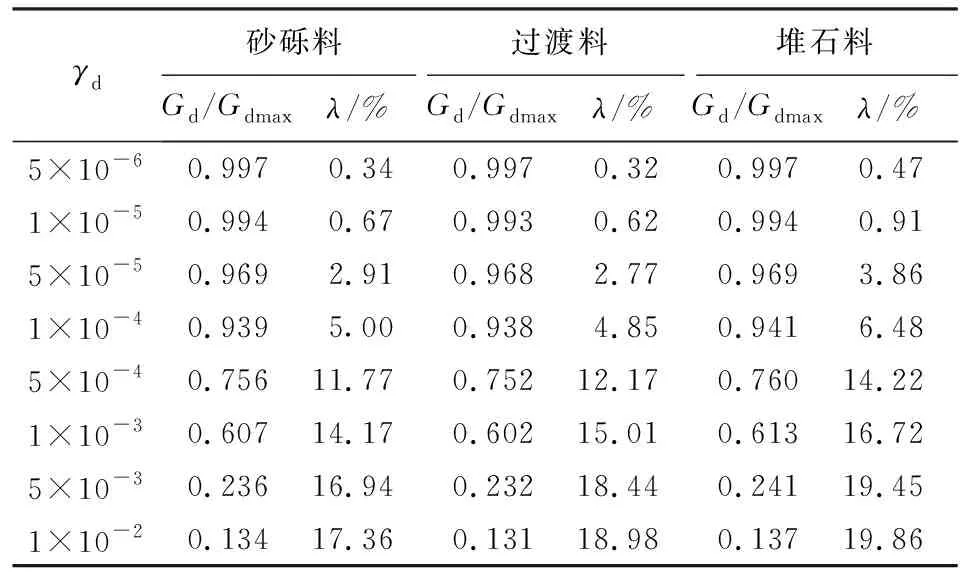
表2 Kc=1.5时归一化的动剪切模量和等效阻尼比

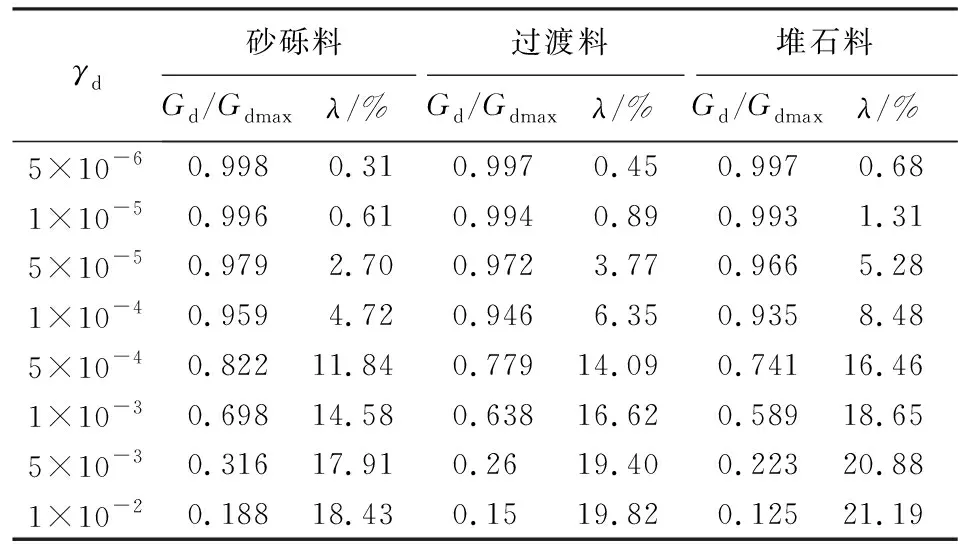
表3 Kc=2.0时归一化的动剪切模量和等效阻尼比

2 坝料永久变形试验

本次永久变形试验共选择2种固结比，3种应力比，按Kc=1.5、σd/σ3=0.5和Kc=2.0、σd/σ3=1.0这2种主要组合进行永久变形试验。试验结果采用大连理工大学邹德高等[15-16]提出的双曲线模型进行整理，坝料残余剪切应变γr与振次N的关系曲线如图6所示。一般而言，循环动应力下粗粒料的残余剪应变与固结比、围压和振次等因素有关。由图6可知，固结比和围压越大，坝料的残余剪切应变越大，初始固结比和围压的增大都会提高试样的密实度，骨料接触更加紧密；随着振次的增加，坝料的残余剪应变不断增加，但其变化速率不断减小，符合衰减规律；由于颗粒破碎效应，堆石料的残余剪切应变明显高于砂砾料和过渡料。

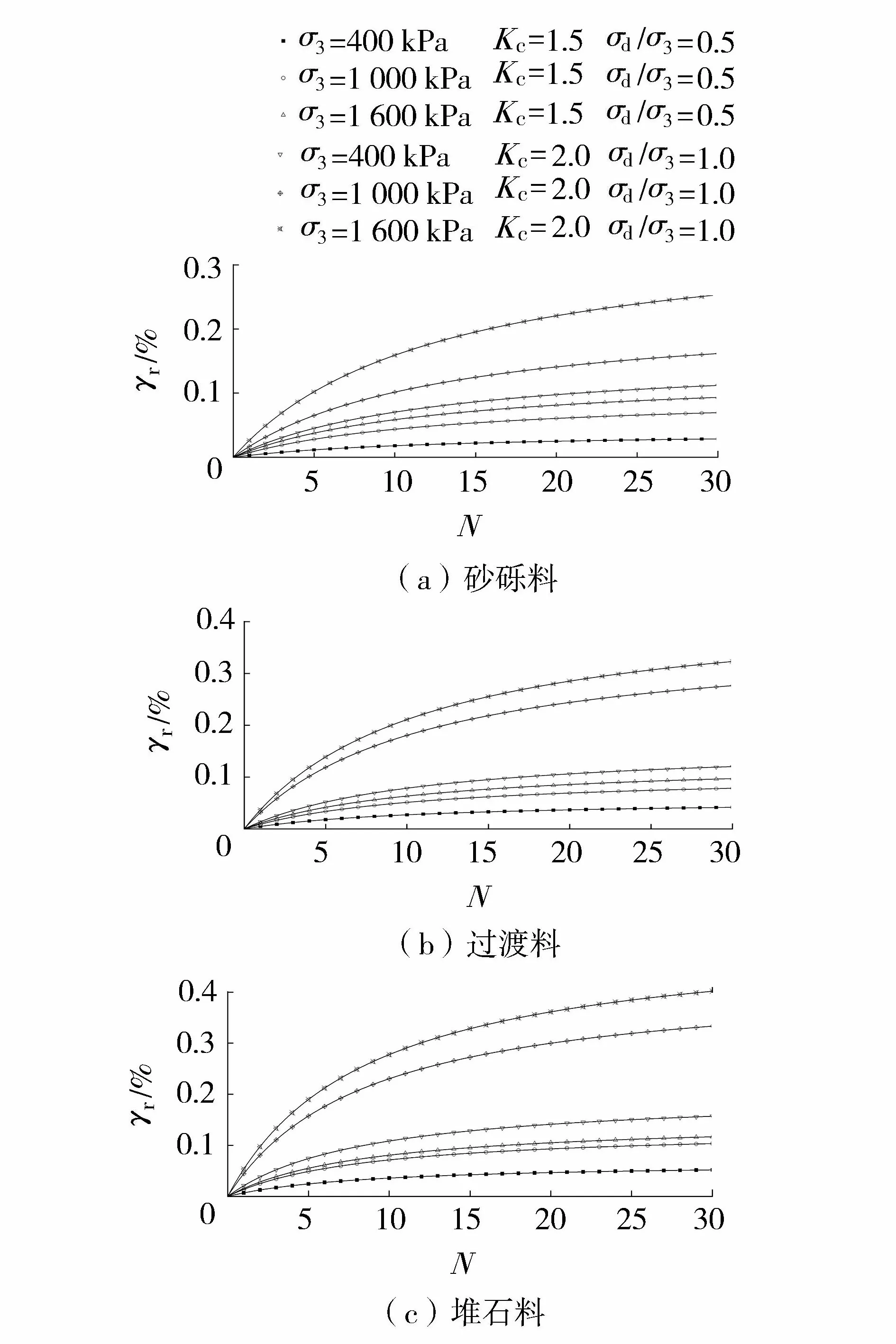
图6 坝料γr-N关系曲线

3 心墙沥青混凝土动力特性试验

3.1 试验方法

根据《尼雅水库碱性骨料沥青配合比报告》[17]，本工程心墙沥青混凝土配合比优选后基础配合比如表4所示。制备∅100 mm×200 mm的沥青混凝土三轴试件，本次试验选取的固结应力比分别为Kc=1.5、1.8、2.1，在围压σ3分别为0.2 MPa、0.6 MPa和1.0 MPa下进行试验。

表4 沥青混凝土设计优选配合比

3.2 结果与分析

根据Hardin-Drenevich模型，对心墙沥青混凝土动三轴试验结果整理如表5所示。围压和固结应力比对心墙沥青混凝土的最大动模量Edmax和最大动剪切模量Gdmax的影响较大。固结应力比相同时，随着围压的增大，沥青混凝土的Edmax和Gdmax增大，但其增幅减小。围压相同时，随着初始固结应力比增大，沥青混凝土材料的Edmax和Gdmax不断增大，初始固结应力比增大使沥青混凝土更加密实，从而提高材料的刚度。

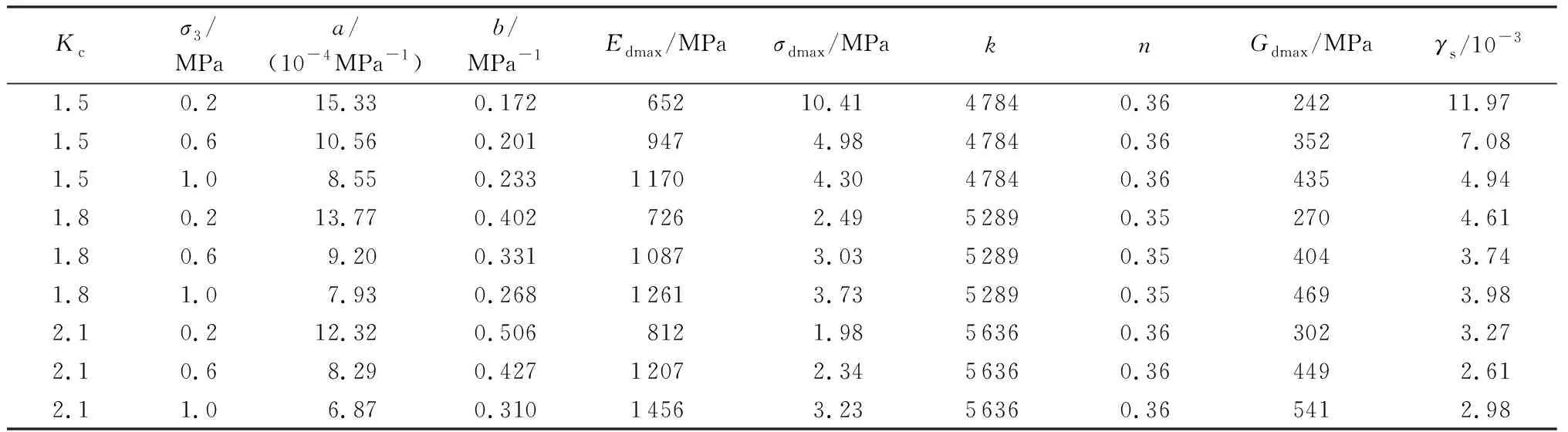
表5 心墙沥青混凝土动三轴试验结果

4 动力分析计算

尼雅大坝坝址处中、小地震相对活跃，周边破坏性地震对场地的最大影响烈度为Ⅶ度，因此分析大坝在地震作用下的动力、变形特性和安全稳定性。

4.1 计算软件介绍

本次三维地震动力反应分析采用大连理工大学自主开发的岩土工程三维静、动力有效应力非线性分析程序GEODYNA极限平衡法稳定计算软件GEOSTABLE和有限元动力法边坡稳定和变形分析软件FEMSTABLE。GEODYNA包含多种连续介质本构模型和接触面模型；GEOSTABLE包含瑞典法和简化Bishop法，可考虑线性强度和非线性强度；FEMSTABLE采用有限元拟静力法和动力法计算土坡稳定安全系数，具有动态滑弧显示功能，可考虑线性强度和非线性强度。

4.2 计算模型及参数

4.2.1几何模型

根据坝体设计横断面，同时考虑该工程复杂的河谷地形条件、大坝材料分区以及分层填筑对大坝应力和变形的影响，建立坝体三维有限元网格如图7所示，沥青混凝土心墙三维有限元网格如图8所示。坝体三维有限元模型单元数为289 831个，节点数为336 612个，自由度超过106。沥青混凝土心墙三维有限元模型单元数为6 689个，节点数为13 822个，坝体典型横断面材料分区如图1所示。

图7 坝体三维有限元网格

图8 心墙三维有限元网格

4.2.2动力计算本构模型

4.2.2.1 坝料

筑坝材料动力计算本构模型采用等效线性黏-弹性模型，筑坝材料最大动剪切模量表示为

(1)

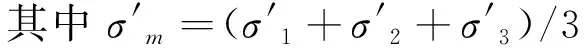
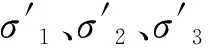
4.2.2.2 接触面

接触面单元的动力模型中，接触面的最大动剪模量为

(2)

式中：σn为接触面单元的法向应力；C为接触面动力剪切试验测得的系数，取22.0。

接触面单元的剪切劲度K与动剪应变γ的关系如下：

(3)

其中τf=σntanδ

式中：τf为破坏剪应力;δ为接触面的摩擦角;参数M=2.0。

接触面单元的阻尼比λ为

(4)

式中：λmax为最大阻尼比，计算中取0.2。

4.2.2.3 地震永久变形计算模型

土石坝地震永久变形分析采用以应变势概念为基础的整体变形计算方法。以往的残余变形模型假定残余应变与振次在半对数坐标下呈线性关系。但残余体应变与振次的关系曲线在半对数坐标下并不是简单的线性关系，初期的体积应变慢于半对数变化规律。采用半对数线性关系会明显低估较大振次处的残余体应变，围压和动应力越大差别越明显，对分析大坝的安全不利。大连理工大学邹德高等[9,15-18]通过研究多种坝料的永久变形试验成果，提出了大工双曲线残余变形模型，该模型的残余体应变和剪应变分别表示为

(5)

(6)

式中：εvr为残余体应变；γr为残余剪应变；Asr为极限的残余剪应变；Bvr和Bsr均为与材料有关的常数。

为避免高估坝顶处体积收缩变形的问题，该模型引入了平均主应力反映残余体积变形规律。将极限状态下的残余体应变εvr表示为平均主应力和动剪应变的函数：

(7)

式中：d1、d2为模型参数；σ0为平均主应力。

对于砂砾料，将Asr表示为动剪应变的函数：

(8)

式中：d3、d4均为模型参数。

4.2.3计算参数

以室内动力三轴试验结果作为本次大坝动力分析的计算参数，坝料动模量和阻尼比参数见表1至表3，心墙沥青混凝土动力参数如表5所示，永久变形计算参数如表6所示。

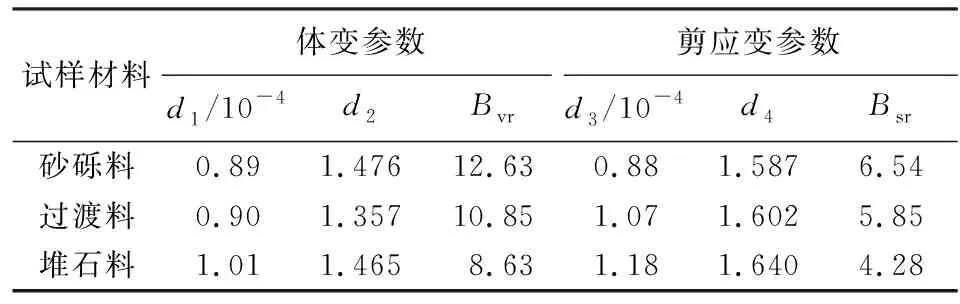
表6 永久变形计算参数

4.2.4地震动输入

高土石坝-河谷山体系统是一个能量开放的系统，山体河谷与坝体之间存在着不同程度的相互作用，外行的散射能量会向无限地基辐射。这些因素会导致坝体边界处各点的反应幅值及相位存在差异，使地震波动效应的影响更加显著。因此，本次有限元计算地震动输入采用黏弹性边界和等效荷载，考虑了大坝和基岩的动力相互作用及辐射阻尼[19]。根据坝址场地地震动参数和GB 51247—2018《水工建筑物抗震设计规范》对标准设计反应谱的规定拟合得到地震时程曲线。设计地震动水平向峰值加速度为0.139g，竖向峰值加速度为水平向的2/3，顺河向、竖向和坝轴向的地震加速度时程曲线如图9所示。动力计算时在模型底部和侧边施加黏弹性边界，以模拟地基无限域辐射阻尼的作用。人工边界通过在边界节点上施加切向和法向的阻尼器来实现，其参数可分别按下式计算：

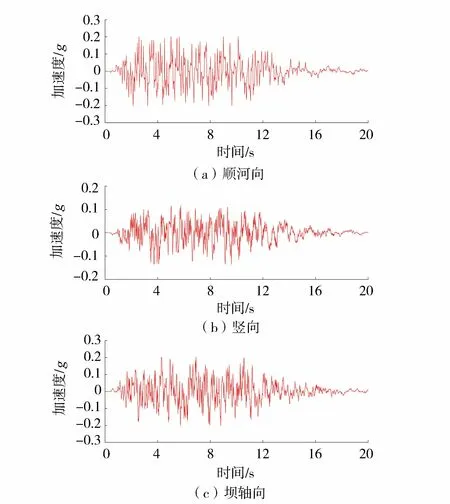
图9 设计地震时程曲线

Ct=ρVsΔAi

(9)

Cn=ρVpΔAi

(10)

式中：ΔAi为模型外边界节点i的控制面积(亦称代表面积)；ρ为节点i处边界材料的密度；Vs、Vp分别对应节点i处边界材料的剪切波速与纵波波速。

4.3 地震动力反应

4.3.1坝体地震反应

坝体各方向动力反应后动位移三维分布如图10所示，加速度三维分布如图11所示，动力反应后的计算结果见表7。由图10可知，随着坝高的增大，坝体各方向的动位移增大。坝体顺河向最大动位移为0.042 m，竖向最大动位移为 0.014 m，坝轴向最大动位移为0.028 m，最大值均出现在坝顶附近。坝体左岸和右岸动位移近似相等且关于坝体中心断面对称。由于河谷基础的约束，岸坡处坝体竖向动位移小于坝顶中心处动位移。由图11可知坝体最大顺河向加速度为4.98 m/s2，最大竖向加速度为3.29 m/s2，最大坝轴向加速度为4.02 m/s2，最大值均位于坝顶部附近。顺河向、竖向、坝轴向加速度放大倍数分别为3.65、2.41、2.95。根据坝体地震反应结果可知坝体顺河向动位移和加速度均最大，地震波可简化为一个垂直向上传播的剪切波(S波)和纵波(P波)以及面波(瑞利波与勒夫波)[20]。S波引起剪应力变化，P波引起正应力变化，S波和P波同时作用使坝体水平方向剪应变增大，地震波对坝体顺河向的影响最大。

图10 地震时坝体各方向最大动位移(单位：m)

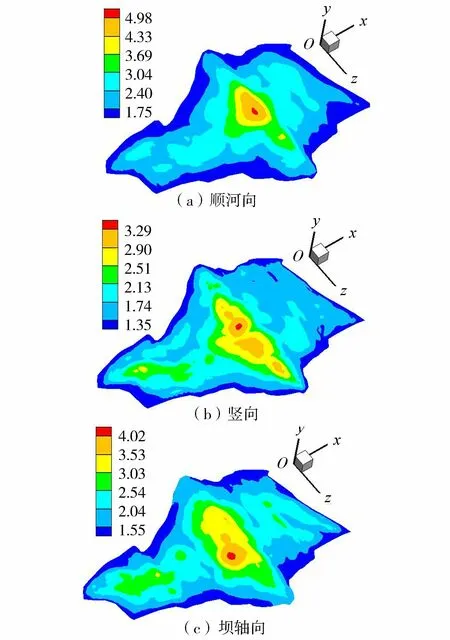
图11 地震时坝体各方向加速度(单位：m/s2)

4.3.2心墙应力

心墙静动叠加应力如图12所示，混凝土心墙静动叠加最大大主应力和最小小主应力均随着心墙深度的增加而增加，且由于受到岸坡的约束，心墙最大压应力为2.46 MPa，出现在心墙与岸坡交界处；最大拉应力为0.05 MPa，出现在心墙的顶部和左岸岸坡处；心墙大小主应力的最大值均位于心墙底部，设计施工时需注意心墙底部的抗剪强度。

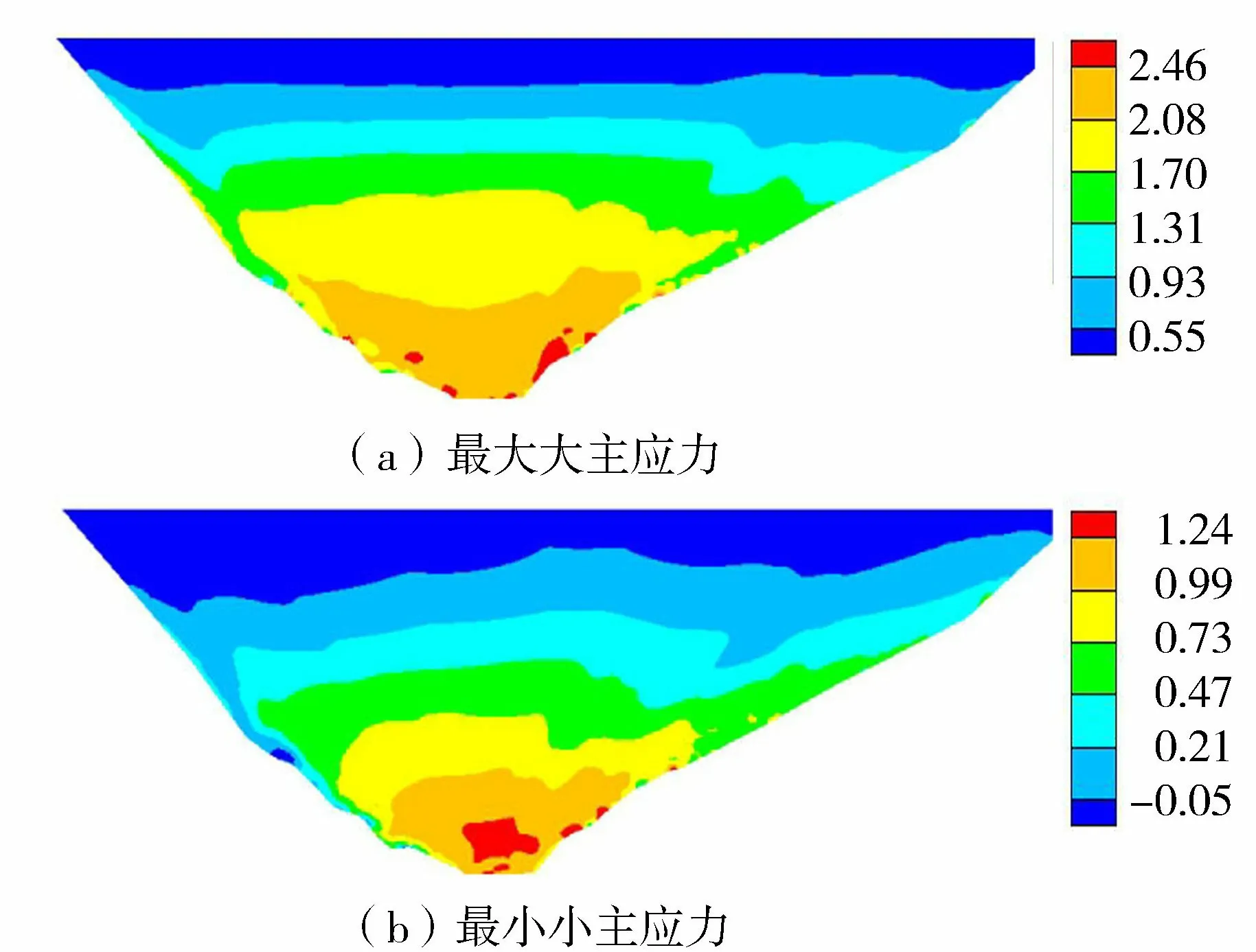
图12 地震作用时应力(单位MPa，以压应力为正)

4.3.3坝体永久变形

根据有限元动力分析的计算结果，对坝体进行三维永久变形计算。计算得到的大坝典型断面位移见图13。由图13可知，随着大坝高度的增加，坝体下游顺河向永久位移增加，且位移变形均为向下游。上游最大永久位移位于上游坡1/2坝高处，顺河向最大位移为0.035 m(向上游)，下游坝体顺河向最大位移在坝顶处，最大位移为0.062 m(向下游)，下游最大位移仅为上游最大位移的1.77倍。由于坝体上下游土体顺河向最大永久变形均为背离坝坡方向，土体受到拉应力作用产生顺河向永久位移，因此坝体上下游土体顺河向均产生拉应力破坏。坝体竖向地震永久变形随着坝高的增加不断增大，均表现为垂直沉降，且竖向永久变形云图表现为层状结构，即坝高相同时坝体竖向沉降量近似相等，地震时坝体不易发生不均匀沉降引起的结构破坏。坝顶最大沉降为0.107 m，约占坝体和覆盖层高度的0.084%，该量值在土石坝正常永久变形范围内，说明“金包银”结构具有良好的抗震效果。

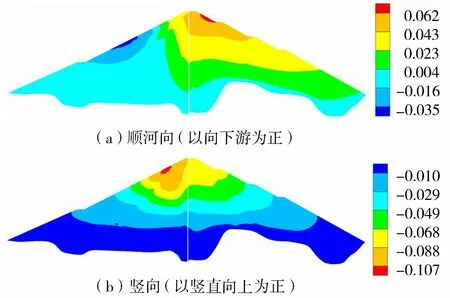
图13 0+150坝体典型断面永久变形(单位：m)

4.3.4心墙永久变形

地震永久变形后心墙应力如图14所示，各方向位移如图15所示，由于受到岸坡的约束，心墙最大压应力为1.92 MPa，仍出现在心墙与岸坡交界处，大小主应力均无拉应力产生。震后心墙3个方向的最大位移均发生在坝顶处，随着心墙高度的增加，心墙竖向永久位移不断增大，心墙竖向永久位移最大值为0.072 m，比两侧坝体竖向永久位移小0.035 m，心墙与坝体同步适应变形的能力较强。沿坝轴向永久位移最大值为0.020 m，沿顺河向永久位移最大值为0.047 m。

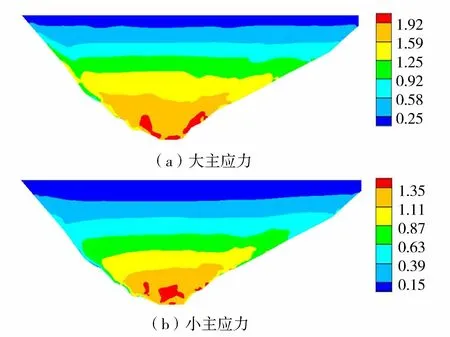
图14 震后心墙应力(单位：MPa，以压应力为正)

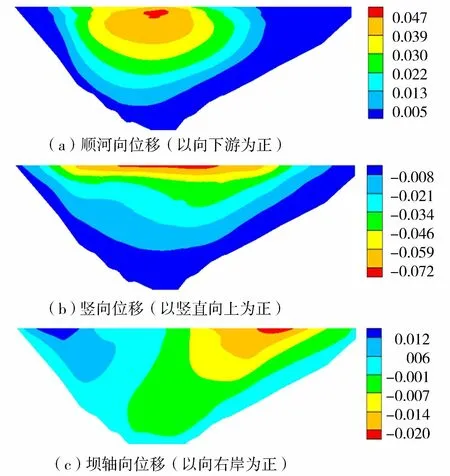
图15 震后心墙各方向位移(单位：m)

4.4 大坝稳定分析

采用极限平衡法计算大坝典型断面在正常运用期遭遇地震的坝坡的稳定性。运用期遭遇地震时，在设计地震波为0.139g工况下，大坝典型断面上游安全系数为2.03，下游安全系数为2.43，安全系数均满足规范规定的安全系数控制值1.2，坝体具有较高的安全储备。

5 结 论

a.砂砾料和过渡料的最大动剪切模量比堆石料高4%～11%，砂砾料和过渡料抵抗变形的能力优于堆石料，而堆石料的最大阻尼比比砂砾料和过渡料高4%～14%，堆石料颗粒间发生错动摩擦产生的应变耗能高于砂砾料和过渡料。

b.围压和固结比对心墙沥青混凝土的最大动模量和最大动剪切模量的影响较大。固结比相同时，随着围压的增大，沥青混凝土的最大动模量和最大动剪切模量增大，但其增幅减小。围压不变时，随着初始固结比的增大，沥青混凝土材料更加密实，从而提高了材料的最大动模量和最大动剪切模量。

c.根据地震动力反应，坝体各方向最大位移、加速度和最大永久变形均发生在坝顶处，顺河向最大位移为0.042 m，最大加速度为4.98 m/s2，最大沉降为0.107 m，坝体上下游顺河向最大永久变形均表现为背离坝坡，顺河向可产生拉应力破坏。心墙大小主应力最大值均发生在底部，竖向永久位移最大值为0.072 m，坝体的最大沉降比心墙高0.035 m，坝体与心墙协调变形能力较强。

d.从筑坝材料动力试验及大坝三维动力分析计算可知，尼雅水库沥青混凝土心墙坝采用“金包银”结构不仅可以有效地利用坝址周边的砂砾料，节约成本，而且使坝体具有良好的抗震性能。