终端区4D飞行轨迹预测与冲突预警

丁松滨， 管吉晨, 刘计民

(1.南京航空航天大学民航学院， 南京 211106; 2.中国民用航空华东空中交通管理局， 上海 200335)

国际民航组织(International Civil Aviation Organization，ICAO)将空中交通管理(air traffic management,ATM)定义为“通过与各方合作，提供设备和服务，对空中交通和空域进行动态、集成管理，以实现安全，经济和高效的目标[1]。随着空中交通需求激增，传统空中交通管制方式弊端日渐增多，空中交通拥堵现象时有发生。因此，基于轨迹运行(trajectory based operation,TBO)的空中交通管理理念应运而生[2]。TBO的核心在于四维轨迹的共享，这不仅要求实时轨迹传输，还要求短时、高精度轨迹预测。借助轨迹预测可以实现飞行轨迹精细化管理，增加空域容量，降低冲突可能性，为空管人员提供辅助决策。

飞行轨迹预测应用广泛，现有航空器飞行轨迹预测方法主要分为三类：一是基于数理统计的预测方法，朱晓辉等[3]将飞机动态数据与飞行意图结合，利用似然估计原理计算飞机在指定时间区间内处于某一空域邻域的概率以预测飞行轨迹；张军峰等[4]构建离散、连续动态航迹预测模型，深入分析飞机原始状态、意图、性能等因素对预测精度的影响，有效降低预测不确定性；Franco等[5]基于对数正态分布的航段平均地速建立概率轨迹预测模型，通过输入航段平均地速，分别计算得到飞行时间与燃油消耗的概率密度函数，成功量化风不确定性对航迹预测的影响。二是基于空气动力学模型的预测方法，王超等[6]提出基本飞行模型，据此建立各航段垂直、水平和速度剖面并实现完整轨迹拟合；Thipphavong等[7]通过实际飞行轨迹数据动态调整爬升阶段飞机动力学方程中飞机重量，有效地提升飞机爬升阶段轨迹预测精度。三是基于机器学习的预测方法，Ayhan等[8]构建了三维网格划分空域，结合气象数据，利用隐马尔可夫模型进行轨迹预测；李楠等[9]利用反向传播(back propagation, BP)神经网络进行短时飞行轨迹多维特征预测，克服了传统动力学方程复杂性问题；Pang等[10]利用近似变分贝叶斯改进神经网络算法应用于飞行轨迹预测，有效减少模型中参数数量；Alligier等[11]利用机器学习理论对11种机型的爬升进行建模以预测爬升阶段飞机的重量和速度。

飞行冲突预警的核心技术在于判断航空器发生潜在冲突的可能性，主要依靠冲突探测实现。现阶段，冲突探测技术分两类，分别是确定型、概率型技术。Hao等[12]利用4DT(4-dimentional trajectory)技术进行飞机动力学建模分析，预测未来航空器轨迹，采用5架航空器进行仿真实验，判断时空棱柱的空间关系，实现冲突探测。

航空器实际飞行过程复杂，传统动力学模型条件过于严苛，对实际飞行轨迹预测效果并不理想，而现阶段基于机器学习的轨迹预测集中于神经网络(neural networks algorithm，NNA)及相关改进算法的研究，但NNA优化目标为经验风险最小，容易陷入局部最优，模型预测不确定性较大，需要大规模、高质量数据进行训练。为此，提出一种基于孪生支持向量回归的4D飞行轨迹预测模型。首先，利用重采样技术降低飞行轨迹数据规模；然后构建训练集输入、输出矩阵，计算得到预测模型；然后建立航空器冲突预警指示函数；最后进行飞行轨迹实时预测，利用回归误差分析进行预测结果检验，并对指定航空器进行安全评估。

1 孪生支持向量回归

孪生支持向量回归(twin support vector regression,TSVR)由Peng改进支持向量回归(support vector regression,SVR)得到，优点在于泛化能力强，且计算效率大幅提高，算法时间复杂度缩短为传统SVR的1/4[13]。本质上，TSVR通过建立原始数据集x的两个二次规划问题(quadratic programming problems,QPPs)求解产生ε-不敏感(ε为误差不敏感度，即误差<ε时，认为误差为0)，上、下限函数分别表示为fupper(x)、flower(x)，最终回归函数f由fupper与flower加权平均得到[14]。为计算fupper和flower，根据QPPs问题建立优化方程为

(Xw1+eb1)]+c1eTξ

s.t.Y-(Xw1+eb1)≥eε1-ξ,ξ≥0

(1)

(2)

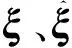
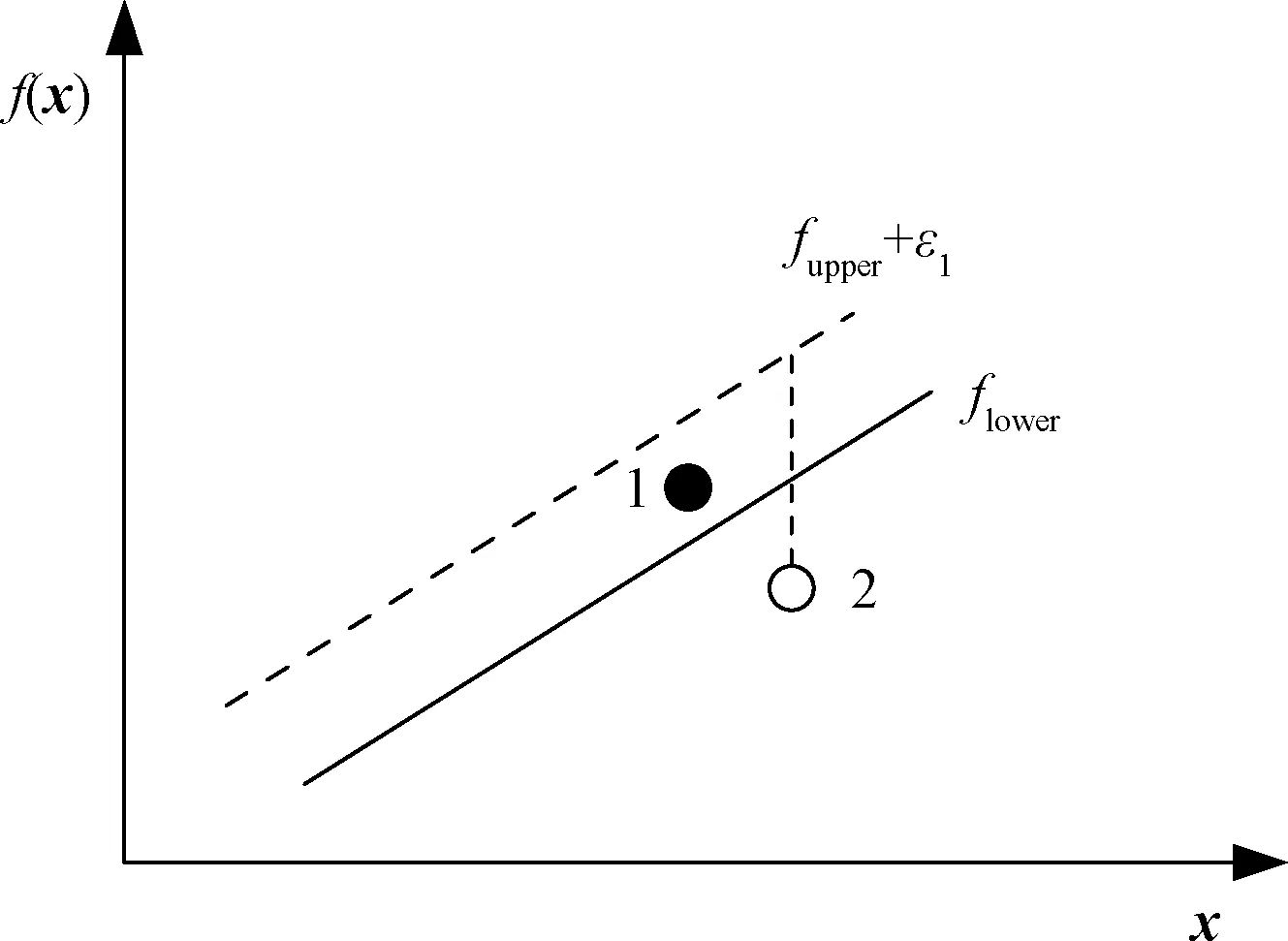
图1 ε不敏感区间Fig.1 The geometric interpretation forε-insensitive interval

在工程领域，由于问题的复杂性，样本集通常呈现高度非线性化，因而线性拟合的实用价值较低。通过引入核函数可以将线性TSVR推广到非线性领域，建立回归函数如式(3)、式(4)所示，下限函数的原优化方程如式(5)所示。

f(x)=a1fupper(x)+a2flower(x)

(3)

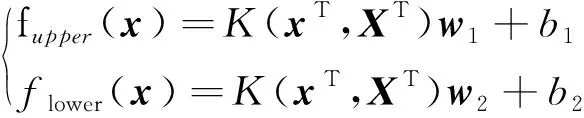
(4)

式(4)中：a1、a2分别为上下限函数权重，且满足a1+a2=1；b1、b2为偏置；K(·)为核函数，常用径向基函数(radial basis function, RBF)。

在有约束的优化问题中，拉格朗日函数是重要的求解方法，通过引入拉格朗日乘子将约束方程转化为自变量，构建无约束优化问题进行求解。因而对优化函数[式(5)]构建拉格朗日函数，并建立其对偶方程，如式(6)、式(7)所示。

[K(X,XT)w1+eb1]}+c1eTξ

s.t.Y-[K(X,XT)w1+eb1]≥eε1-ξ,ξ≥0

(5)

eb1]}T{Y-eε1-[K(X,XT)w1+eb1]}+

c1eTξ-αT{Y-[K(X,XT)w1+eb1]-eε1+

ξ}-βTξ

(6)

s.t.0≤α≤c1e

(7)

式中：α和β为拉格朗日乘子，满足α>0，β>0；H=[K(X,XT)e]；f=Y-eε1；L(·)为损失函数。

逐次超松弛技术是一种用于求解大规模线性方程组的迭代算法[15]，文献[16]中指出，逐次超松弛技术可以求得QPPs收敛解。因而，运用该算法求解式(7)得到w1、b1，同理求得w2、b2，最终建立回归函数f(x)。

2 飞行轨迹预测模型

2.1 飞行轨迹重采样

由于ADS-B设备以秒为单位与飞机通信并存储数据，因而存在大量冗余数据，为提高模型计算速度，拟采用时间间隔Δt对飞行轨迹进行重采样。重采样算法如图2所示。

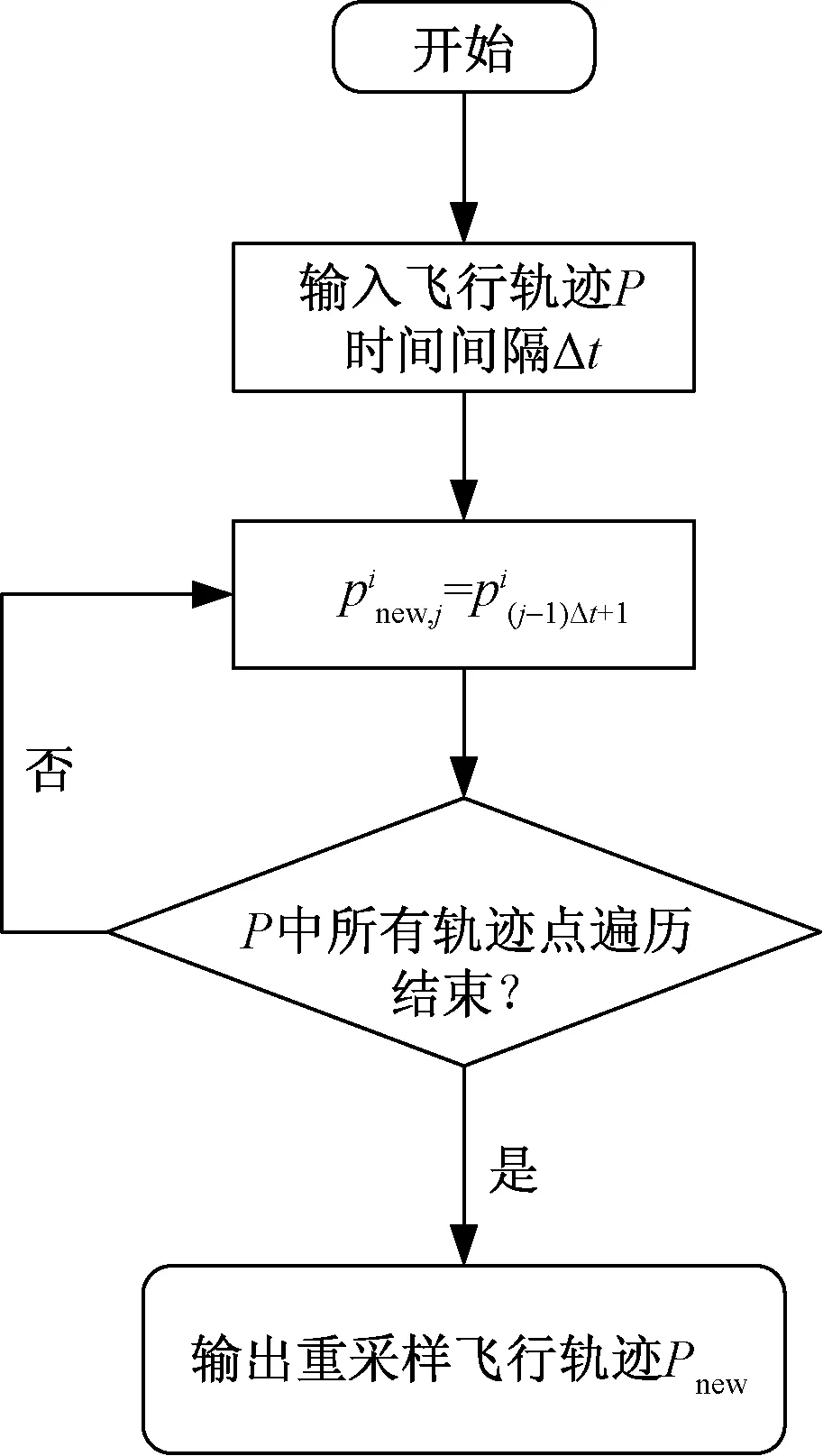
为第i种属性第j个新飞行轨迹点；为第(j-1)Δt+1 个原始飞行轨迹点；Pnew为由重采样轨迹点集组成的飞行轨迹图2 飞行轨迹重采样流程Fig.2 Resampling process of flight trajectory

重采样前后航空器轨迹对比如图3所示。红色圆点表示原始飞行轨迹，时间间隔1 s；○为重采样飞行轨迹，时间间隔10 s。通过飞行轨迹重采样能够在保留原始飞行轨迹特征的前提下有效降低数据规模，提升计算速度，增强预测的实时性。

1 ft=3.048×10-1 m图3 重采样与原始轨迹对比Fig.3 Contrast of resampling and raw trajectory

2.2 预测模型构建

根据预测步长可以定义航空器轨迹预测提前量φ(t)，若是单步预测，则预测提前量为两相邻轨迹点时间间隔，若是多步预测，则为起始预测点与最终预测点时间间隔。

在TSVR飞行轨迹预测模型构建过程中，需要训练集样本进行模型训练，设训练集输入矩阵XTrain维度l×k，训练集输出矩阵YTrain维度l×1。其中，l为训练集输入、输出样本数目，最终飞行轨迹预测流程如图4所示。

3 航空器冲突预警指示函数

高精度轨迹预测为航空器未来态势感知提供保障，可应用于短时冲突分析，降低管制员工作负荷，提升空中交通智能化水平。在终端区内，水平间隔与垂直间隔是常用的管制调配手段，通过调整航空器水平、垂直间隔避免冲突发生，可有效保证航空器安全运行。航空器最小水平间隔为6 000 m，最小垂直间隔是300 m，如图5所示。由此定义航空器冲突预警阈值I(A,B)[17]可表示为

(8)

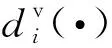
通过引入航空器冲突预警指示函数，将4D飞行轨迹预测与任意两个给定航班之间的安全评估相结合。若轨迹预测模型计算短时轨迹距离小于安全间隔阈值，则可以提醒管制员和飞行员采取适当的措施以增加安全系数。

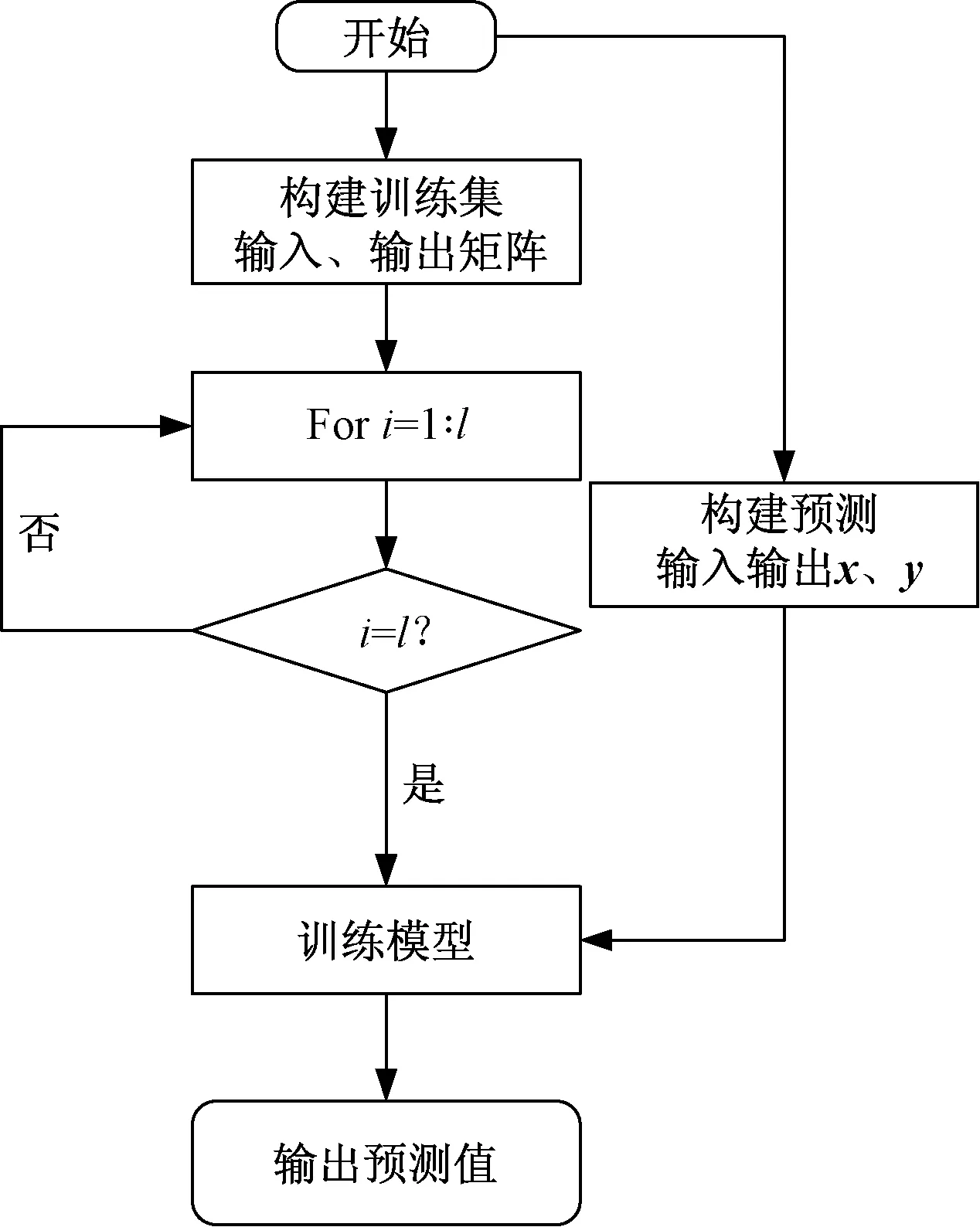
i为训练集样本序号图4 飞行轨迹预测流程Fig.4 Flow of flight trajectory prediction

4 实验分析

选取天津滨海机场进近航空器4条进场轨迹(CCA1318、CHB6237、CGZ7147、CXA8209)进行实验分析，进近航空器多机动动作，轨迹变化明显，具有良好的分析价值。迭代方法为单步迭代，经重采样轨迹点时间间隔为10 s，因为轨迹预测提前量为10 s。实验环境Windows10操作系统，2.4 GHz CPU，8 GB内存，实验软件MALTAB2018a。

4.1 数据预处理

ADS-B只能记录飞机的经纬度信息，为进行航空器飞行间隔计算，需将经纬度转化为直角坐标。拟以机场基准点(aerodrome reference point,ARP)为原点，采用Jenny[18]建立空间直角坐标系，正北、正东为纵轴(y轴)、横轴(x轴)，立轴(z轴)坐标即高度值(单位：ft)，转化示例如表1所示。

表1 航班部分坐标转换对比

轨迹数据的x-y-z坐标量纲不同，直接计算影响预测精度，因而采用归一化算法消除量纲影响，数据归一化算法可以提高计算效率，增强预测能力，拟采用min-max标准化算法，其计算公式为

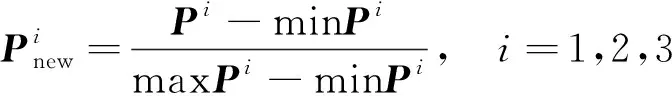
(9)

4.2 预测评价指标

回归预测分析需要指标进行误差评价，以对比模型的优劣。在线性回归模型中，通常采用决定系数，但在高维非线性问题中，该指标常出现大于1的情况，无法正确评价模型。因而，拟综合采用残差、平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)进行模型有效性评估。

(10)

(11)

(12)

4.3 预测结果

图6(a)、图6(b)、图6(c)分别为航班CCA1318航班x坐标、y坐标和z坐标时序预测图，截取部分展示，其中x坐标的预测时段是710～850 s，y、z坐标的预测时段分别是610～850 s和60～400 s。图6(d)是为轨迹三维预测图。

图6 飞行轨迹预测结果Fig.6 Prediction results of flight trajectory

参数选择：训练集样本个数l=5，样本属性k=2，惩罚系数c1=c2=2-5，惩罚系数c3=c4=0.001，核函数带宽σ=10，间隔ε=0.001。由图6可知，TSVR算法能够准确预测目标轨迹点，有效识别航空器运动趋势。

4.4 模型残差分析

针对图6轨迹预测进行误差分析，计算模型残差如图7所示。图7(a)、图7(b)、图7(c)分别为x、y、z坐标预测残差。由图7(a)、图7(b)可知，x、y坐标预测最大残差分别是801、537 m，由图7(c)可知，高度残差最大为243 ft。虽然x坐标预测残差较大，但大部分轨迹点坐标预测残差集中在600 m内，仅存在几处异常值，说明模型总体预测能力较强，满足实际空中交通管理精度需求，且在该实验中模型参数一致，针对不同实验对象，预测效果均表现优秀，说明模型泛化能力较强，具有较高的实际应用价值。

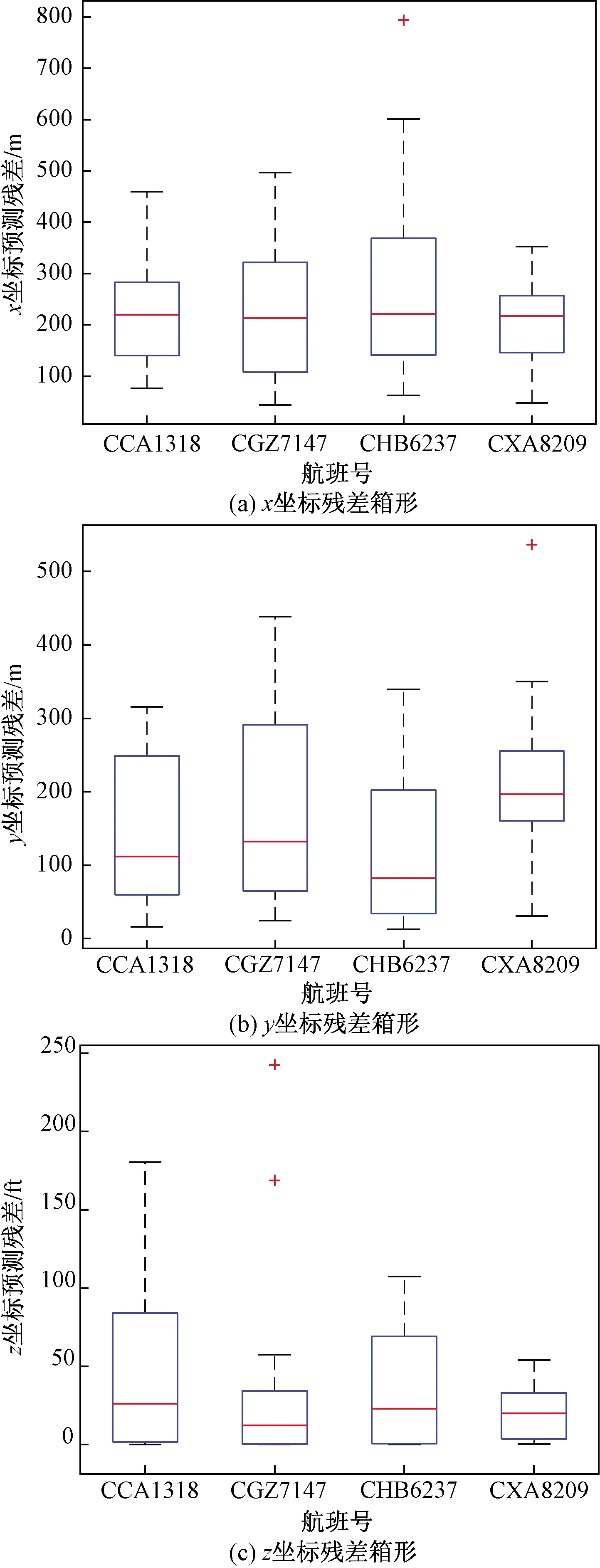
+表示离群值图7 飞行轨迹预测残差Fig.7 Predction error of flight trajectory

4.5 航空器冲突预警

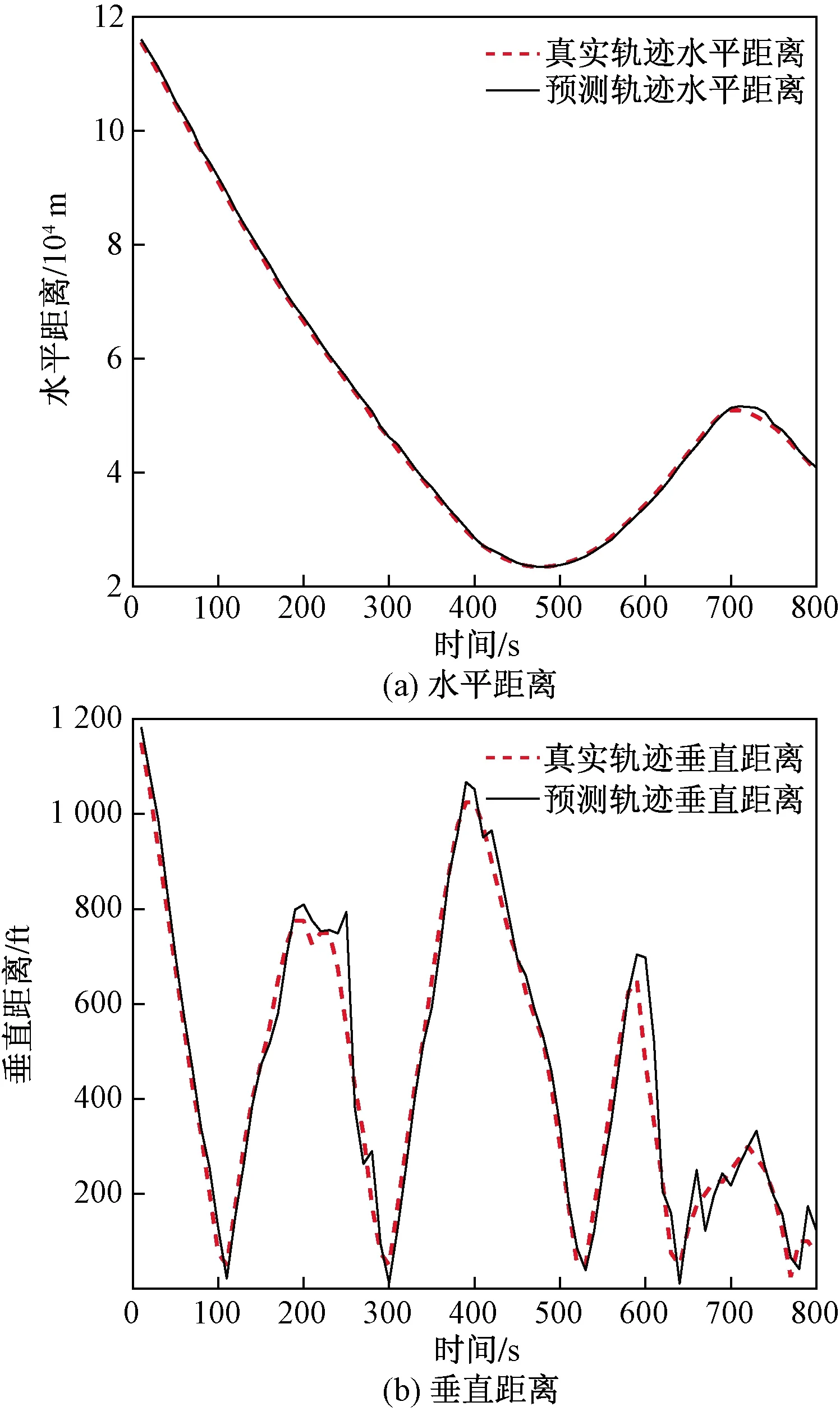
图8 轨迹间距离对比Fig.8 Comparision of distance between two trajectories

4.6 多算法对比

机器学习中，除支持向量机(support vector machine，SVM)之外，还有神经网络及相关改进算法、贝叶斯算法、集成学习(以随机数、随机森林为代表)等，其中，以神经网络的应用最为广泛。在航空器轨迹预测领域，较多学者采用神经网络或相关改进算法进行研究分析。为对两种主流算法进行对比，现引入反向传播(back propagation，BP)神经网络进行预测实验，其中BP神经网络参数选择为隐含层神经元数目10，最大迭代次数100，学习率0.15，误差阈值0.000 01，预测轨迹点数目80。最终对比结果如表2所示。

表2 TSVR和BP算法MAE、RMSE对比

通过对比可知，3种属性，4条轨迹，两种误差算法所得TSVR误差值均小于BP神经网络算法，其中，以MAE评估x坐标预测误差平均减少505 m，y坐标、z坐标预测误差分别减少419 m和42 ft，以RMSE评估则分别减少577、350 m、29 ft，证明TSVR预测精度优于BP神经网络。此外，实验中TSVR算法百次运行时间平均值约为2.37 s，单轨迹点预测耗时0.03 s，BP神经网络则为12.53 s，单次耗时0.16 s，证明TSVR算法计算效率高，综上所提出基于TSVR轨迹预测模型具有优良的性能。

4.7 参数灵敏度分析

超参数的引入是机器学习算法的重要特征，超参数无法通过模型训练得到，需要提前设置，因而，超参数的取值对模型的计算效果有重要影响。在TSVR算法中包含ε、c1、c2、c3、c4、σ，设置c1=c2，c3=c4。此外，在预测环节，训练集样本个数l、样本属性k同样属于超参数。

以CXA8209轨迹x距离为实验数据，对超参数进行赋值，以探究超参数对模型精度的影响，实验结果如图9所示。超参数取值如表3所示。

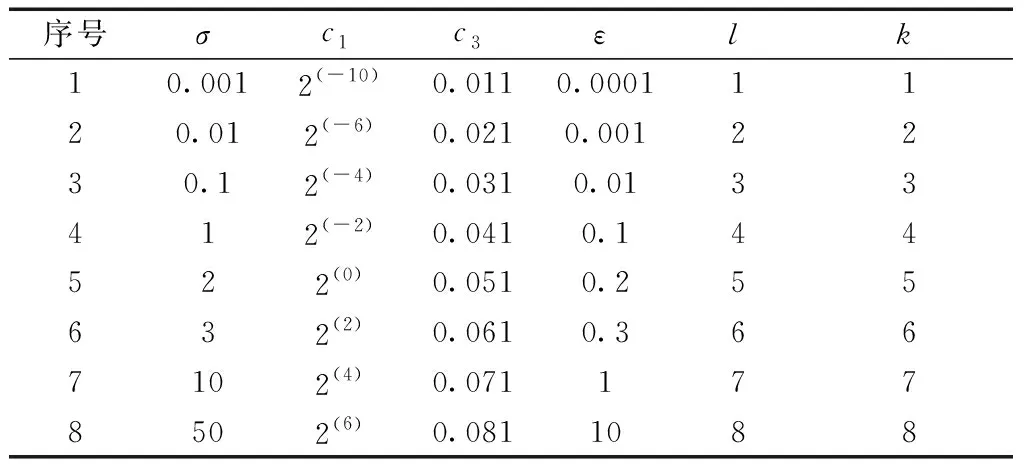
表3 超参数取值

图9中，核函数带宽σ、惩罚系数c1、c3对模型预测精度影响较大。随着σ取值增大，预测模型模型RMSE误差取值先减小后增大，表明模型预测精度先增加后降低，而随着c1、c3取值增大， RMSE逐渐增大，模型预测精度逐渐降低。间隔ε和样本属性k对精度影响较小，ε、k增大RMSE基本不变，而训练样本数目l增大，RMSE减小，模型预测精度逐渐提升，但当l>3时，模型精度基本不变。

图9 参数灵敏度检验Fig.9 Sensitivity analysis of parameters

5 结论

基于孪生支持向量回归算法建立航空器飞行轨迹实时预测模型以实现航空器短时冲突预警。首先，利用重采样算法进行轨迹预处理，降低数据规模，提升模型计算效率。然后，基于历史飞行轨迹点进行回归函数训练，建立4D飞行轨迹预测模型，采用递归预测的思想，实现飞行轨迹的动态预测。最后，建立航空器冲突预警指示函数，判断两航空器间潜在飞行冲突。基于TSVR的飞行轨迹预测模型能够克服传统空气动力学建模困难的问题，仿真实验证明，模型泛化能力强，数据需求较小，避免大规模数据训练，相较于BP神经网络算法预测精度更高、计算速度更快，具有良好的实用价值。仅对模型中超参数进行灵敏度分析，未来考虑超参数优化以实现更为精准的预测效果。