滚轮滚针轴承螺栓强度优化设计方法
2021-10-21李鑫斌姜艳红丁士钊
张 剑, 李鑫斌, 姜艳红*, 丁士钊, 刘 静
(1.中浙高铁轴承有限公司, 龙游 324400; 2. 重庆大学机械与运载工程学院, 重庆 400044; 3.西北工业大学航海学院, 西安 710072; 4.西北工业大学无人水下运载技术工业和信息化部重点实验室, 西安 710072)
滚轮滚针轴承通常在民机襟翼和缝翼等部件中作为滚轮使用[1]。与一般滚针轴承相比,滚轮滚针轴承内圈主要采用螺栓与滑轮架连接,其内圈和螺栓为一体化结构,外圈可在滑轨上滚动,为滑轮架在滑轨上滑动提供滚动支撑[2]。滚轮滚针轴承螺栓内部注油孔与螺栓外面圆角的结构和尺寸将改变滚轮滚针轴承螺栓的应力和变形,影响滚轮滚针轴承的使用寿命。因此,开展滚轮滚针轴承注油孔与螺栓外面圆角结构和设计参数优化方法研究,减小轴承螺栓的应力和变形,提高滚轮滚针轴承的使用寿命。
在滚动轴承优化设计方面,已经有众多学者开展了相关研究。孙玉飞等[3]以轴承额定动载荷为优化设计目标,对深沟球轴承节圆直径、钢球直径和数量进行了优化设计。张亚军等[4]以油膜厚度、接触应力和变形量为优化目标,建立了轴向载荷下的圆柱滚子轴承多目标优化模型,确定了滚子端面和挡边最佳的位置参数。Waghole等[5]采用人工蜂群算法、差分搜索算法、网络搜索法以及混合方法,以滚针轴承动态承载能力最大为优化目标,对滚针轴承滚子直径、滚子长度和滚子数等参数进行优化设计。Zhao等[6]建立了钢丝球轴承优化设计数学模型,以摩擦力矩最小为优化目标,对球数、球的直径、节圆以及接触角进行了优化设计。Charitopoulos等[7]以减小摩擦力矩为优化目标,考虑轴承区域的散热、共轭散热以及润滑油区域的剪切减薄和气穴现象,提出了一种基于计算流体动力学(computational fluid dynamics,CFD)的热流体力学计算方法,对推力轴承兜孔进行了优化设计。莫易敏等[8]采用遗传算法,以降低圆锥滚子轴承摩擦力矩为优化目标,对圆锥滚子轴承的节圆直径、滚子直径、滚子有效长度、外圈接触角、滚子半锥角以及滚子端面与内圈挡边面的接触高度进行优化设计。闫轩等[9]构建了温度影响的球轴承动力学模型,采用主成分分析法对预紧力与轴承动态指标间的耦合关系实施动态降维优化。张强强等[10]建立了一种适用于高转速脂润滑条件的生热模型及传热模型,以降低轴承外圈温度为优化目标,对轴承转速进行优化。赵方伟等[11]以降低轴向轴承温升为优化目标,采用试验方法对轴承载荷和转速进行优化。张功学等[12]建立了轴承总成内腔的数值分析模型,分析了轴承运动对流畅内部气相流动的影响,揭示了转速对轴承总成腔内的传热特性的影响,从而对轴承转速进行优化。综上所述,目前的研究主要集中在球轴承、圆柱滚子轴和圆锥滚子的结构进行优化设计。虽然少量研究对滚子轴承的结构进行了优化,但是在滚轮滚针轴承螺栓结构参数的优化设计方面研究较少。
针对这一问题,以螺栓最大应力和变形为优化目标,提出了滚轮滚针轴承螺栓强度优化设计方法。首先,基于三维建模软件,建立了滚轮滚针轴承参数化模型;然后,运用有限元方法,提出了滚轮滚针轴承整体有限元仿真模型,分析了注油孔设计参数和螺栓上圆角设计参数对螺栓强度的影响规律;最后,采用响应面分析方法,建立了以螺栓最大应力和最大变形最小为优化目标的滚轮滚针轴承多目标优化模型,获得了螺栓注油孔孔径和螺栓上圆角的最优化设计参数。
1 优化设计方法描述
因响应面优化(response surface optimization)方法具有计算快且精度高等优点,在各种机械零件的结构优化优化设计中获得了广泛的应用[13-18]。因此,论文采用响应面法对滚轮滚针轴承螺栓结构进行优化设计。该优化算法的流程,如图1所示。算法的具体步骤包括:①在三维建模软件Solidworks中对滚轮滚针轴承进行参数化建模;②在有限元分析软件ANSYS Workbench中建立滚轮滚针轴承整体有限元模型,并对其进行静力学分析;③在AYSYS Response Surface Optimization模块中构建优化系统,对滚轮滚针轴承螺栓注油孔和圆角设计参数进行优化设计;④对选用的优化参数进行验证,确定其合理性。

图1 优化设计方法流程图Fig.1 Flow chart for the proposed optimization method
2 参数化建模
滚轮滚针轴承的注油孔分为三段。各段注油孔优化参数代号,如图2所示。对这三段注油孔设计参数进行多参数优化,各选取参数的优化设计范围,如表1所示。
3 有限元分析
3.1 有限元模型
滚轮滚针轴承的外圈和滚针材料为G20Gr2Ni4,螺栓、机架以及隔离套材料为GGr15Z。两种材料的力学性能,如表2所示[19]。滚轮滚针轴承的网格划分主要采用四面体主导的网格划分方法(Tetrahedrons),将单元尺寸设置为2 mm,网格质量定义为High,圆角处的网格尺寸设为0.25 mm,进行细化。轴承整体有限元模型,如图3所示。该模型有102 255个单元和168 524个节点。
3.2 接触及边界条件
滚轮滚针轴承运行过程中,滚针和滚针、滚针和外圈以及滚针和内圈之间一般为滚动摩擦,故设置滚针和滚针、滚针和外圈以及滚针和内圈之间的接触类型为Frictional,摩擦系数设为0.05。外圈和螺栓、机架和螺栓以及机架和隔离套之间为滑动摩擦,故设置外圈和螺栓、机架和螺栓以及机架和隔离套之间的接触为Frictional,摩擦系数设为0.2。根据滚轮滚针轴承的运行条件,轴承是靠螺栓连接固定在机架上的,因此在螺栓有螺纹一端和机架上添加固定约束(图4中的A位置),在轴承外圈上添加z轴负方向的-11 000 N的力,(图4中B位置)。

图4 滚轮滚针轴承边界条件Fig.4 The boundary condition of the tack roller needle roller bearing
3.3 仿真结果分析
通过对该滚轮滚针轴承进行静力学分析计算,得到螺栓滚轮滚针轴承的整体应力云图、螺栓应力云图和变形云图,如图5~图7所示。
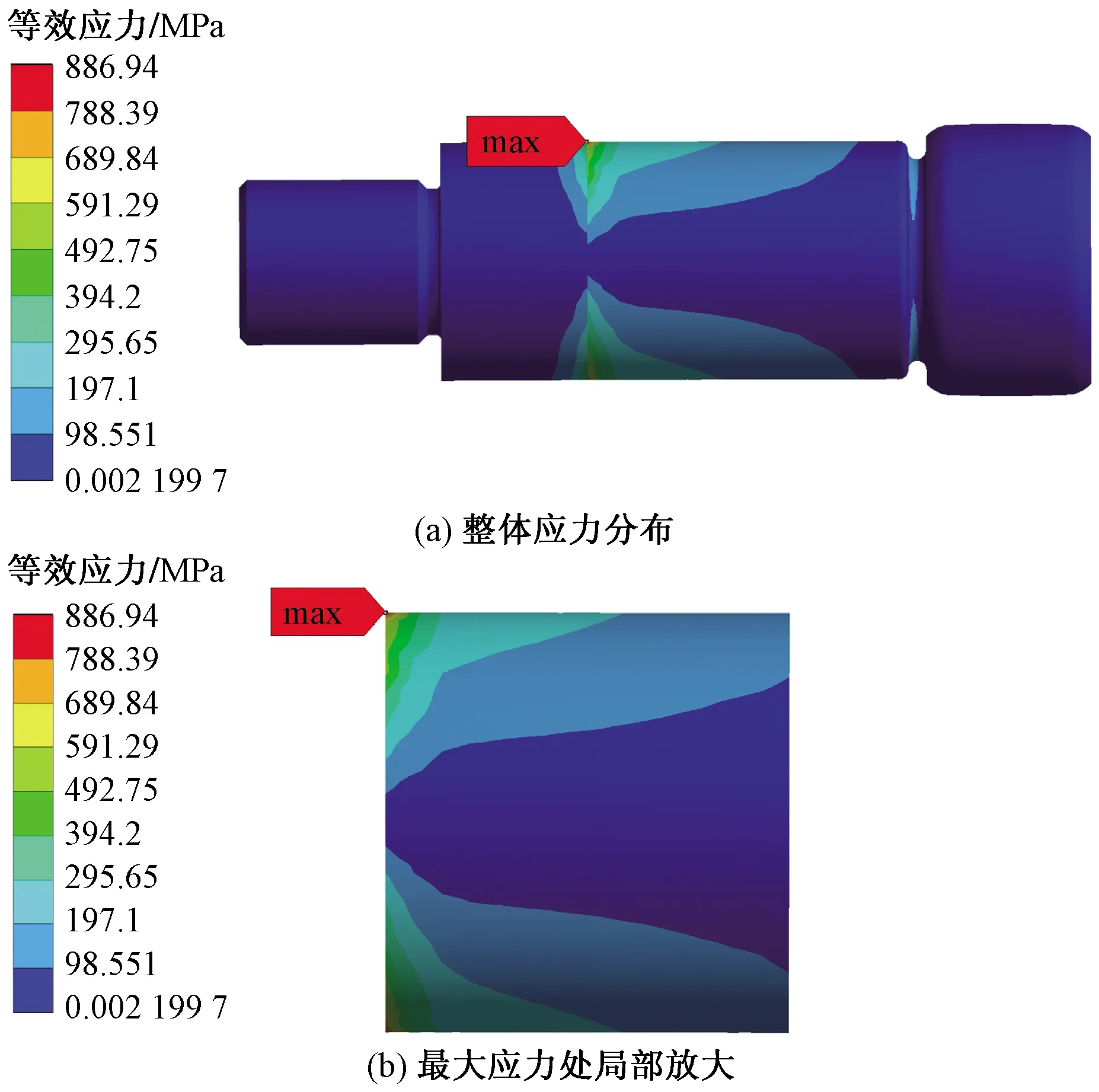
图5 滚轮滚针轴承应力云图Fig.5 The stress distribution of the tack roller needle roller bearing

图6 螺栓应力云图Fig.6 The stress distribution of the bolt

图7 螺栓变形云图Fig.7 The deformation distribution of the bolt
图5~图7显示,滚轮滚针轴承的最大应力为886.94 MPa,位于隔离套与机架的接触处,该值小于GGr15Z的屈服强度1 815 Pa。螺栓最大应力为247.68 MPa,位于滚针一端与滚道的接触处,该值小于GGr15Z的屈服强度1 815 Pa;其最大变形为0.132 92 mm,位于外力施加处。结果表明,该滚轮滚针轴承的强度满足设计要求。
4 基于响应面法的滚轮滚针轴承结构优化设计
4.1 响应面法优化原理
响应面是一个输出参数用输入参数表示的变性质函数,可通过若干个实验确定输出参数与输入参数的近似关系,从而快速得到所有设计实验的输出参数近似值,不需要执行所有的设计实验。响应面的精度取决于解变化的复杂性、原始设计实验的点数和响应面类型等因素。
响应面的主要类型有:基因聚类算法、标准响应面-全2阶多项式、克里格法、非参数回归法、神经网络以及稀疏网格法。论文采用基因聚类算法[20-21],该方法是一种基于遗传算法生成不同类型的响应面同时求解的方法。响应面的适应度函数用于确定最优的响应面,它既考虑了设计点上响应面的精度,又考虑了响应面的稳定性(交叉验证)。遗传聚合响应面可以是单个响应面,也可以是多个不同响应面的组合(通过遗传算法中的交叉操作获得)。
利用不同模型的加权平均,可将基因聚类算法响应面表示为
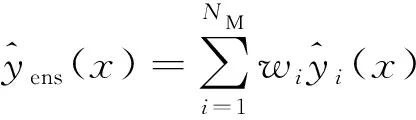
(1)
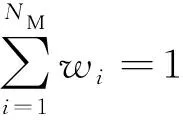
(2)
式(2)中:wi≥0,1≤i≤NM。
为了获得最佳权重因子值,需将设计点的均方根误差(root mean squared error,RMSE)最小化,并对相同设计点的均方根误差进行交叉验证(PRESSRMSE)。RMSE和PRESSRMSE的表达式分别为

(3)
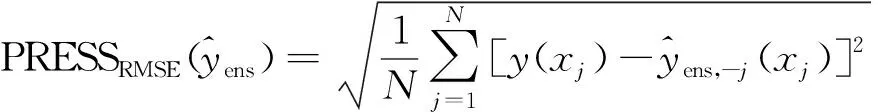
(4)

(5)

4.2 轴承结构设计参数的灵敏度分析
在所建立的响应面为为中,轴承结构设计参数的敏感性分析结果,如图8所示。其中,横坐标为轴承的结构设计参数,纵坐标为灵敏度,灵敏度值越大,说明该设计参数对其影响越大。如图8(a)所示,单独考虑各参数时,D6、D8和D9对螺栓最大应力的影响均为正效应,选取参数的灵敏度为:D9>D6>D8;D8对螺栓最大变形的影响为负效应,D6和D9对螺栓最大变形的影响为正效应,其中在建立的响应面中,D6和D8对螺栓最大变形的影响很小,选取参数的灵敏度为:D9>D8>D6。
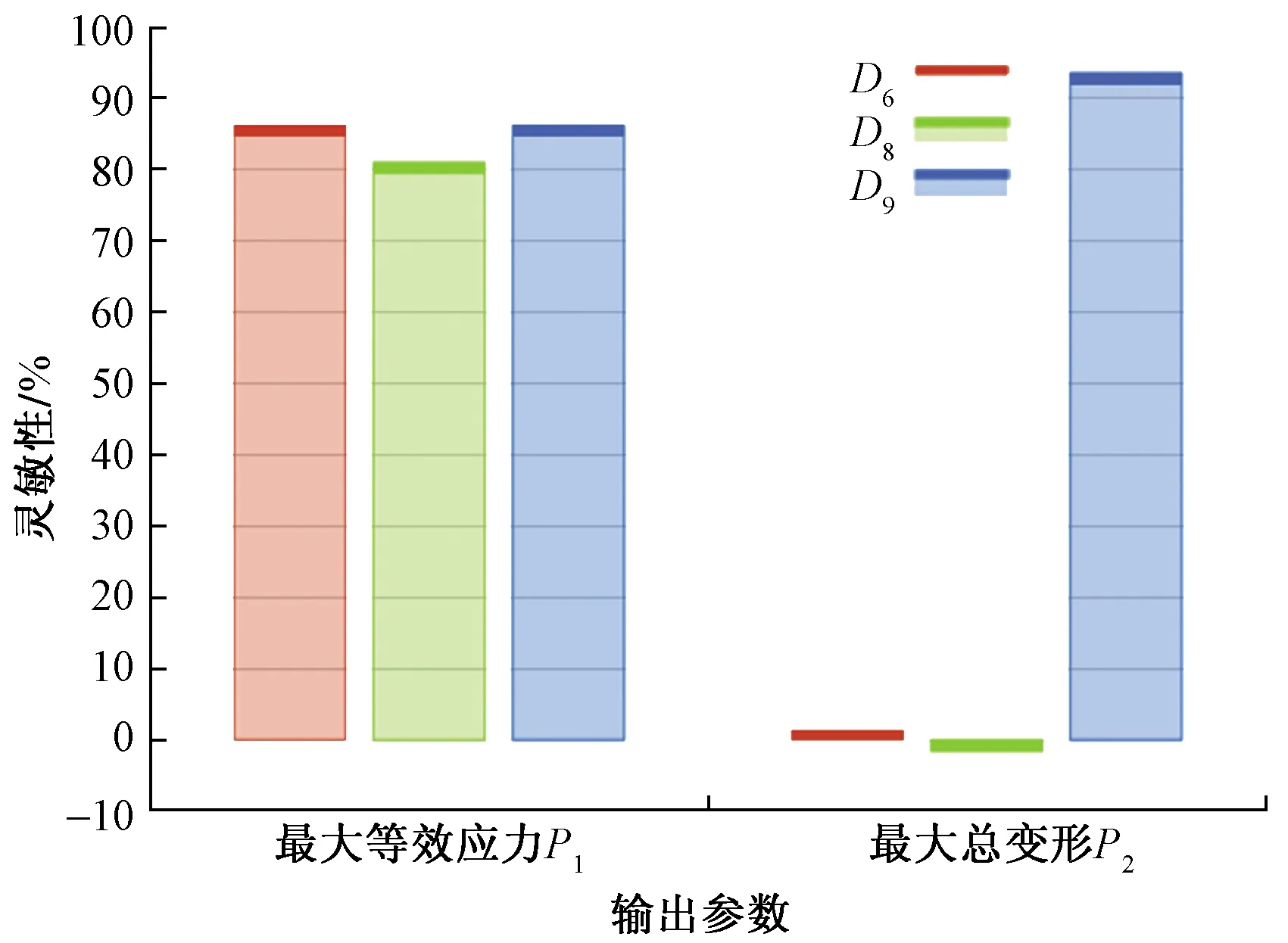
图8 优化参数灵敏性分析Fig.8 The sensitivity analysis of the optimized parameters
5.3 响应面中各参数螺栓最大应力及最大变形的影响规律
在建立的响应面中,轴承各优化参数对螺栓最大应力以及最大变形的影响规律,如图9、图10所示。图9(a)中,油孔孔径D9小于2.2 mm时,螺栓最大应力随着注油孔孔径D9的增加而增加,D9大于2.2 mm时,螺栓最大应力随着注油孔孔径的增加而减小。图9(b)中,油孔孔径D8小于1.25 mm时,螺栓最大应力随着注油孔孔径D8的增加而增加,D8大于1.25 mm时,螺栓最大应力随着注油孔孔径的增加而减小。图9(c)中,在注油孔半径D6小于1.56 mm时,螺栓最大应力随着D6的增加而增加,当D6大于1.56 mm小于1.63 mm时,螺栓最大应力随着D6的增加而减小当D6大于1.63 mm时,螺栓最大应力随着D6的增加而增加。
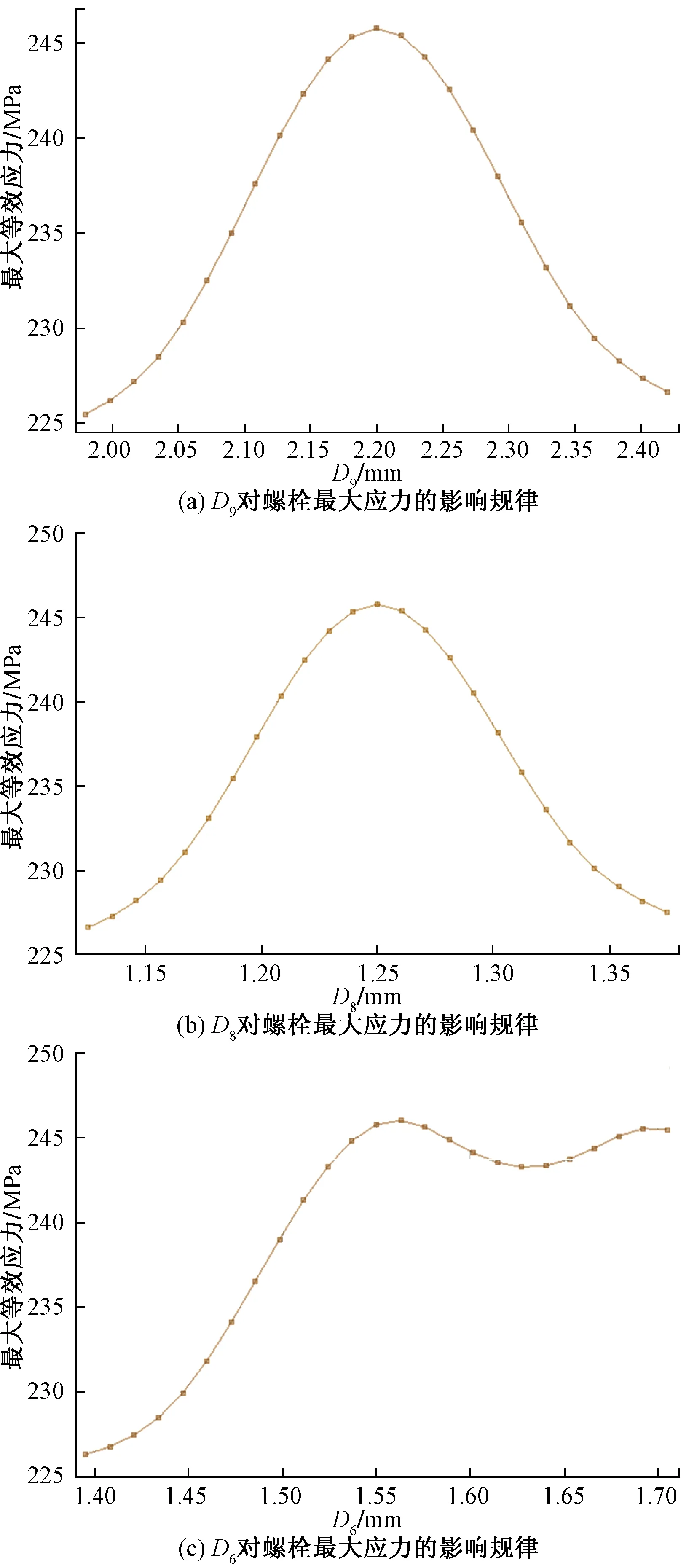
图9 优化参数对螺栓最大应力的影响规律Fig.9 The effect of optimized parameters on the bolt maximum bending stress
图10(a)中,螺栓最大变形随着注油孔孔径D9的增加而增加。图10(b)中,D8小于1.19 mm时,螺栓最大变形随着注油孔孔径D8的增加而增加,D8大于1.19 mm时,螺栓最大变形随着D8的增加而减小。图10(c)中,注油孔半径D6小于1.66 mm时,螺栓最大变形随着D6的增加而增加,注油孔半径D6大于1.66 mm时,螺栓最大变形随着D6的增加而减小。
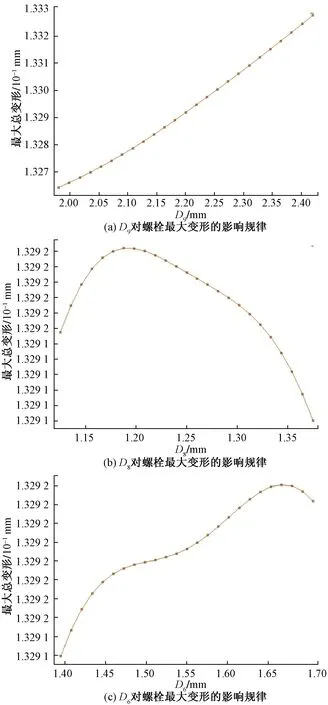
图10 优化参数对螺栓最大变形的影响规律Fig.10 The effect of optimized parameters on the bolt maximum bending deformation
图11为建立的响应面的拟合度分析,可以看出,最大等效应力和最大总变形绝大部分都分布在所建立的响应面附近,仅有两个最大等效应力偏离较大,说明所建立的响应面质量满足要求。
4.4 优化结果分析
本次优化的目标是:螺栓最大应力最小以及螺栓最大变形最小,优化后Workbench给出的三组注油孔孔径推荐孔径如表3所示。根据工程实际,Workbench推荐的参数可能无法加工,因此,对推荐参数进行了修正,以达到加工要求,注油孔孔径修正参数如表4所示。

表3 注油孔孔径优化后推荐数值
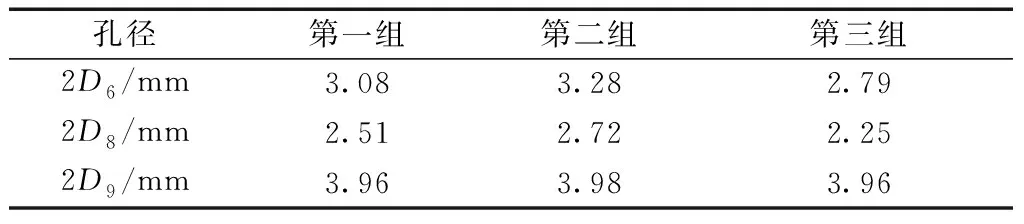
表4 注油孔孔径修正数值
4.5 优化结果验证
根据表4中注油孔孔径修正参数对滚轮滚针轴承的注油孔和螺栓圆角结构设计参数进行修正,分别进行静力学分析。三组修正孔径参数的螺栓应力云图和变形云图,如图12~图14所示。第一组修正参数的螺栓最大应力由247.68 MPa下降至229.21 MPa,下降幅度为7.46%,螺栓最大变形由0.132 92 mm下降至0.132 61 mm,下降幅度为0.23%;第二组修正参数的螺栓最大应力由247.68 MPa下降至228.15 MPa,下降幅度为7.89%,螺栓最大变形由0.132 92 mm下降至0.132 61 mm,下降幅度为0.23%;第三组修正参数的螺栓最大应力由247.68 MPa下降至228.2 MPa,下降幅度为7.86%,螺栓最大变形由0.132 92 mm下降至0.132 64 mm,下降幅度为0.21%。各组修正参数与未优化的螺栓最大应力和最大变形对比结果,如表5所示。综合三组分析结果,建议选用第二组修正参数作为螺栓滚轮滚针轴承的注油孔孔径参数。
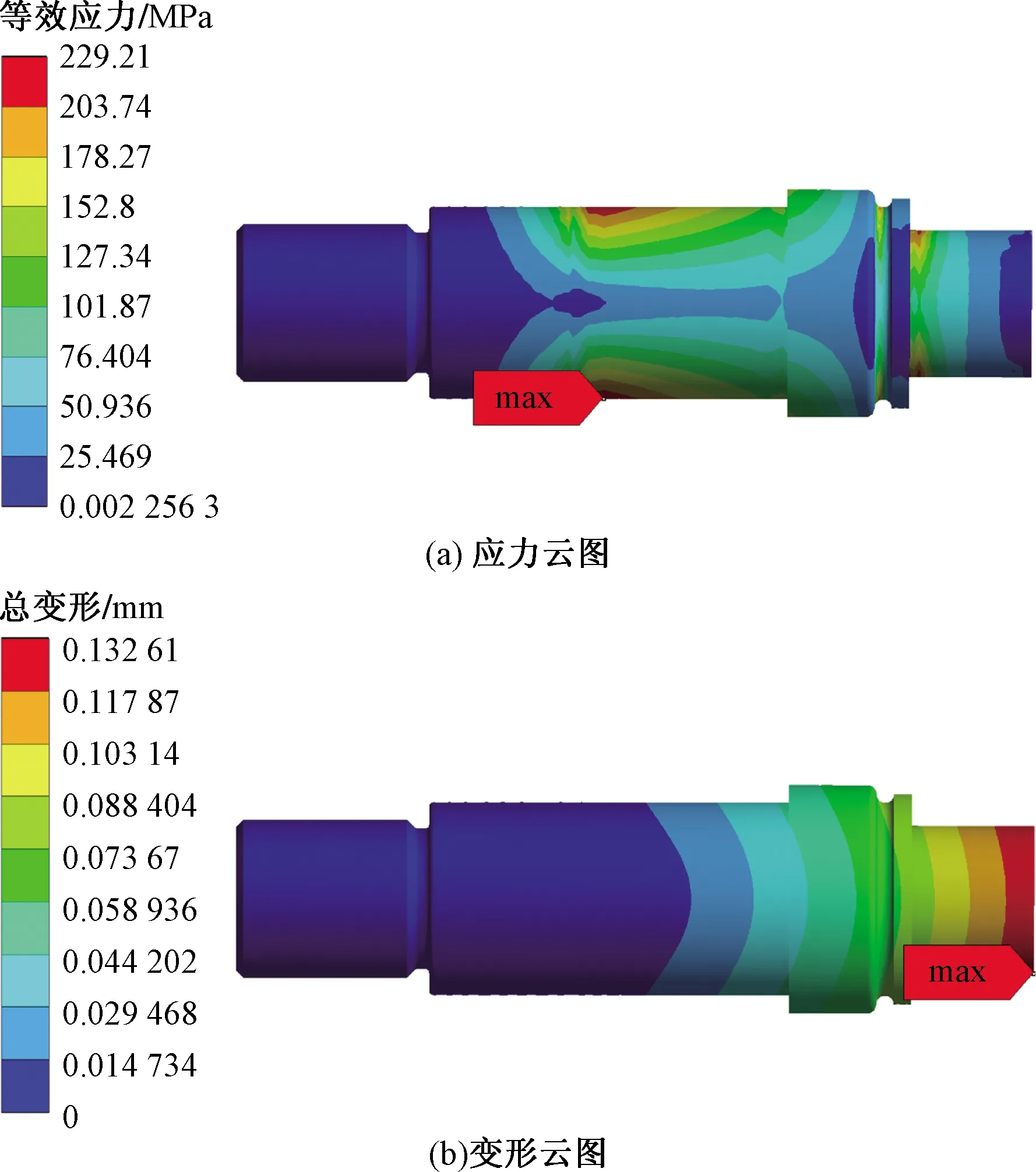
图12 第一组修正参数螺栓应力云图、变形云图Fig.12 The first group of correction parameters bolt stress nephogram, deformation nephogram
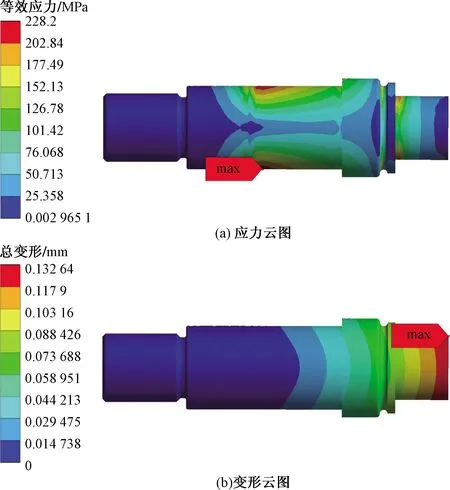
图13 第二组修正参数螺栓应力云图、变形云图Fig.13 The second group of correction parameters bolt stress nephogram, deformation nephogram
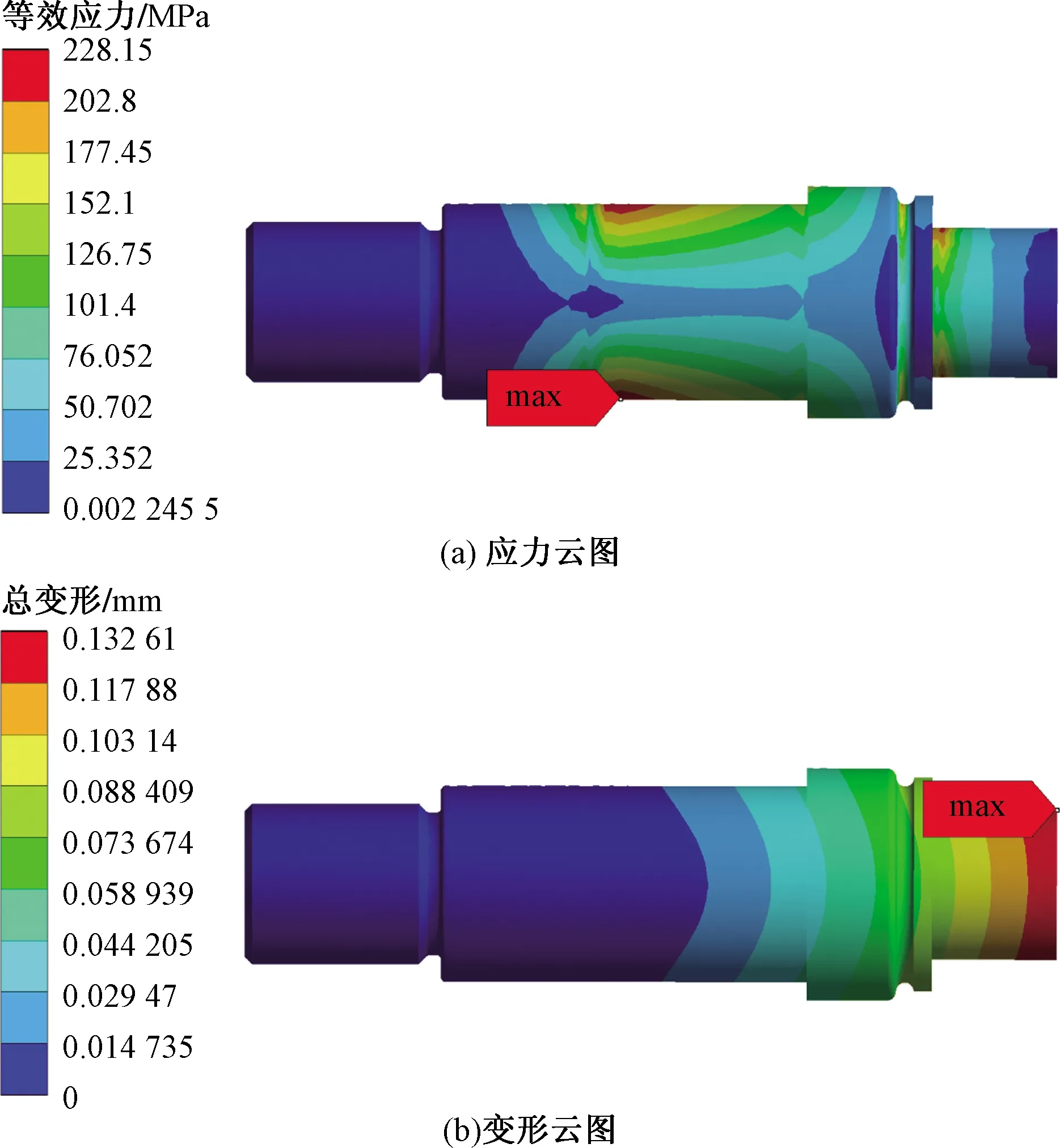
图14 第三组修正参数螺栓应力云图、变形云图Fig.14 The third group of correction parameters bolt stress nephogram, deformation nephogram

表5 各组修正参数与未优化的螺栓最大应力和 最大变形对比
此外,可以看出,修正参数的螺栓最大应力位置发生了改变,未优化前的螺栓最大应力出现在滚针一端和螺栓的接触处,而三组推荐参数的螺栓最大应力出现在螺栓和机架的接触处附近。这可能是因为优化后的螺栓变形减小,导致滚针偏斜量减小,从而导致滚针和螺栓之间的挤压减小,造成螺栓最大应力位置的改变。
6 结论
以螺栓最大应力和变形为优化目标,提出了滚轮滚针轴承螺栓强度优化设计方法,对滚轮滚针轴承注油孔设计参数进行了优化设计,得出如下主要结论。
(1)滚轮滚针轴承的最大应力出现在隔离套与机架的接触处,滚轮滚针轴承螺栓最大应力为出现在滚针一端与滚道的接触处,最大变形出现在外力作用处。
(2)在所建立的响应面中,D6、D8和D9对螺栓最大应力的影响均为正效应,选取参数的灵敏度为:D9>D6>D8;D8对螺栓最大变形的影响为负效应,D6和D9对螺栓最大变形的影响为正效应,D6和D8对螺栓最大变形的影响很小,选取参数的灵敏度为:D9>D8>D6。
(3)在建立的响应面中,D8和D9对滚轮滚针轴承螺栓最大应力的影响规律均为:螺栓最大应力先随其增加而增加,之后随其增加而减小。D6对滚轮滚针轴承螺栓最大应力的影响规律为:螺栓最大应力先随D6的增加而增加,当D6达到1.56 mm后,随D6的增加而减小,当D6达到1.63 mm后,随D6的增加而增加。D6和D8对滚轮滚针轴承螺栓最大变形的影响规律为:螺栓最大变形先随其增加而增加,之后随其增加而减小。D9对滚轮滚针轴承螺栓最大变形的影响规律为:螺栓最大变形随其增加而增加。
(4)结合工程实际,推荐了三组注油孔孔径设计参数。当螺栓滚轮滚针轴承采用这三组修正孔径参数时,螺栓最大应力相比于优化前下降8%左右,最大变形相比于优化前有所下降。综合三组参数的验证结果,建议选用第二组修正参数作为螺栓滚轮滚针轴承的注油孔孔径设计参数。
