不同位移时滞反馈控制对车身减振的影响
2021-10-21马克辉任传波张永国周鹏程陈雅洁
马克辉, 任传波, 张永国, 许 震, 周鹏程, 陈雅洁
(山东理工大学交通与车辆工程学院, 淄博 255000)
随着汽车技术的发展,人们对车辆乘坐的舒适性有了更高的要求。为了适应不同路面工况,人们在传统被动悬架的基础上开发出了各种可控的主动悬架。但是在所有的主动悬架控制系统中,车辆状态传感器数据采集时间、悬架系统振动控制量计算时间、作动器的响应时间等都不可避免地存在滞后现象[1]。时滞不仅会降低控制精度,甚至会导致稳定性的丧失和分岔混沌现象的发生。为避免时滞其对控制系统的不利影响,文献[2-3]对系统时滞进行补偿。然而,有些学者发现将时滞作为一种状态反馈控制量,有意识的控制其大小,使之与反馈系统合理的搭配,则能有很好的减振效果。
许多学者对振动控制系统中的时滞问题做了大量的研究。Olgac等[4-5]将时滞反馈作为输入量应用在吸振器上,构成一个“时滞动力吸振器”,通过仿真表明含时滞反馈的吸振器的减振效果优于被动吸振器。Zhao等[6]、赵艳影等[7]以利用时滞主动控制的积极作用,研究了时滞动力吸振器在非线性振动系统中对主系统的减振效果。Sun等[8]通过试验验证了时滞减振的有效性。陈龙祥等[9-10]平研究了柔性梁旋转运动与受迫振动的时滞主动控制。随后,陈龙等[11]研究了时滞对半主动悬架的影响。付文强等[12]探究了含时滞天棚阻尼半主动悬架控制系统的渐进稳定性机理。朱坤等[13]基于轮胎位移时滞反馈控制提高车辆悬架的性能。闫盖等[14]考虑了悬架系统的固有时滞,利用状态变化法将时滞反馈应用于车辆悬架控制。赵艳影等[15]研究了高速列车车体为反馈对象的非线性时滞反馈控制。吴凯伟等[16]将轮胎位移时滞反馈控制应用于提高车辆座椅的舒适性。
综上所述,尽管时滞减振理论在车辆悬架应用中已经有了较大的进展。目前研究大多是基于模型某一时滞反馈对车身减振的影响,而对不同状态反馈之间的区别鲜有研究。为此,分析了车身位移和轮胎位移时滞状态反馈特性及稳定性区间。在稳定性区间内对控制参数进行优化,并分别在不同外部激励下对时滞反馈控制的主动悬架进行了仿真验证,探索了不同时滞反馈控制对车身减振的影响。
1 1/4车辆主动悬架系统模型
1.1 主动悬架模型的建立
将车辆模型简化为含时滞反馈控制的1/4车辆主动悬架模型,如图1所示。
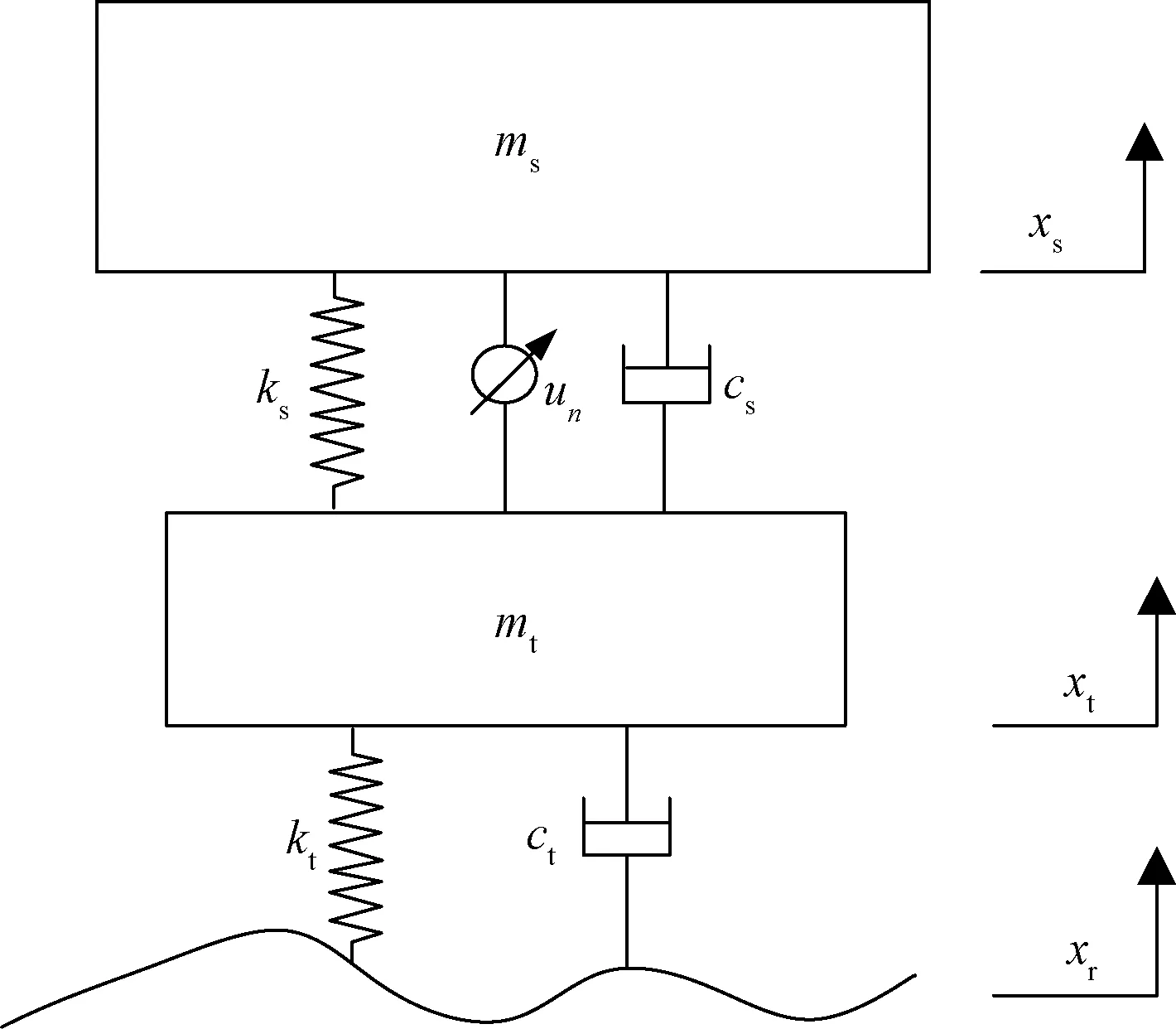
ms、mt分别为车身质量和轮胎质量; ks、cs分别为悬架的刚 度和阻尼系数;kt、ct分别为轮胎的刚度和阻尼系数;xs、xt 和xr分别为车身质心、轮胎质心和外部垂直激励位移;un(n=s, t) 为时滞控制力,当n=s时,表示车身位移时滞反馈控制, 当n=t时,表示轮胎位移时滞反馈控制图1 时滞反馈控制主动悬架模型Fig.1 Active suspension model with time-delay feedback control
利用该模型来研究不同位移时滞反馈控制对车身减振的影响,车辆悬架模型参数如表1所示。

表1 车辆系统模型参数
以xs、xt为广义坐标,根据拉格朗日法可列出1/4车辆含时滞状态反馈控制悬架的动态方程为
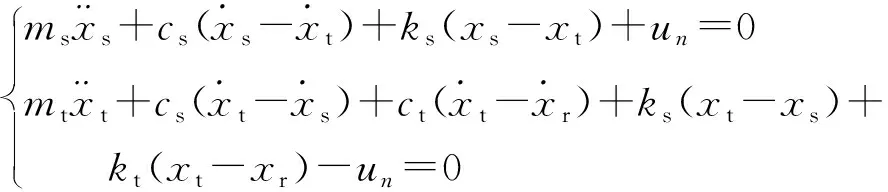
(1)
式(1)中:ut=gtxt(t-τt)为轮胎位移时滞反馈控制;us=gsxs(t-τs)为车身位移时滞反馈控制;gs、gt分别为车身和轮胎反馈控制增益系数;τs、τt分别
为车身和轮胎位移反馈控制时滞量;t为时间。
1.2 系统模型无量纲化
为了便于获得系统的稳定区间,对式(1)进行无量纲化,可表示为
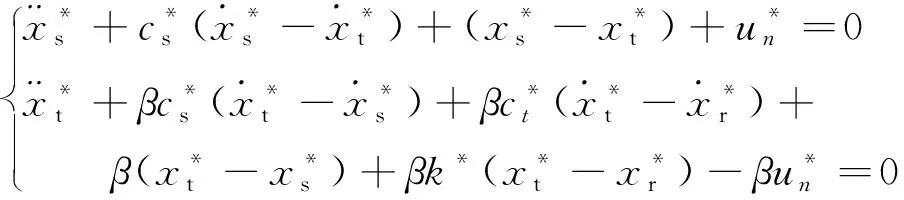
(2)
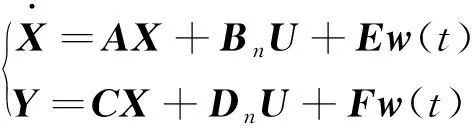
(3)
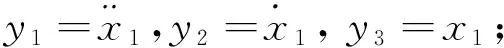
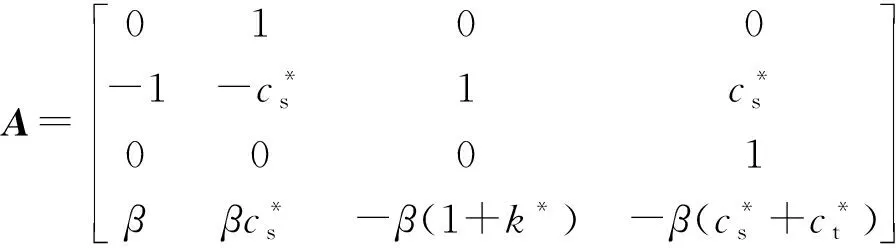
(4)
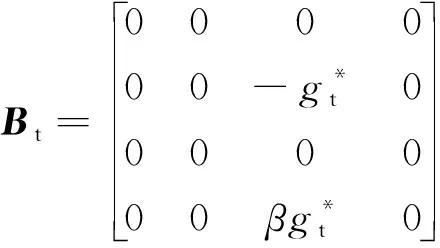
(5)
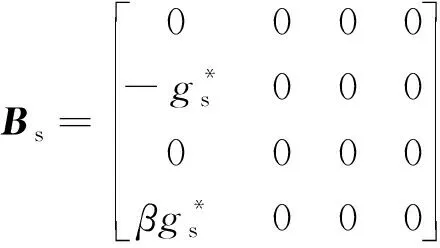
(6)
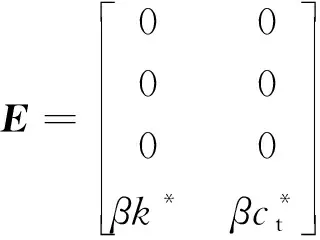
(7)

(8)

(9)
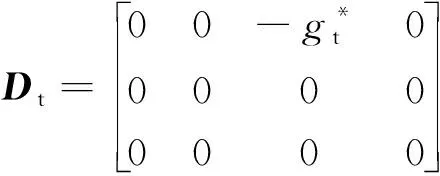
(10)
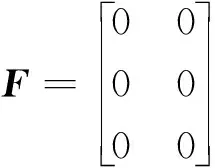
(11)
通过式(2)可以将表1车辆悬架模型参数转化为无量纲化的参数如表2所示。
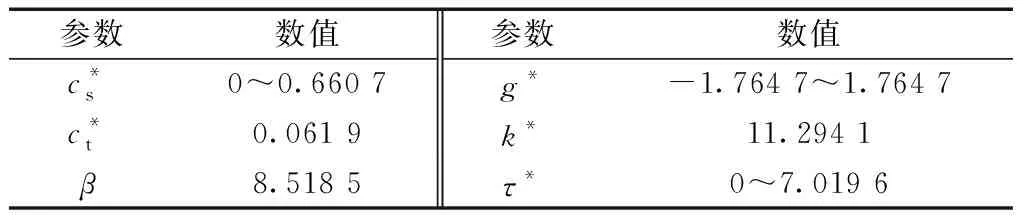
表2 无量纲模型参数
2 稳定性分析
2.1 稳定性分析方法
根据时滞微分方程理论,可得系统的特征方程为
det(sI-A-Be-sτ)=0
(12)
式(12)中:s为方程的特征根;I为单位矩阵。
由式(4)可得特征方程的展开多项式为
D(s,τ)=P(s)+Q(s)e-sτ=0
(13)
式(5)中:D(s,τ)为变量为s、τ的多项式;P(s)、Q(s)为实系数多项式。
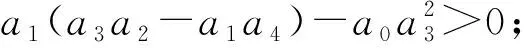
当系统仅满足①时,系统的稳定性是发生切换的。对于条件①的判别比较容易。判断条件②的方法可以通过利用欧拉公式e-iw0τ=cos(w0τ)-isin(w0τ)对D(iw0,τ)=0进行化简。将s=iw0代入式(5)分离多项式P(iw0),实部和虚部,分别表示如下:PI(w0)=Im[P(iw0)],PI(w0)=Im[P(iw0)];分离多项式Q(iw0)实部和虚部,分别表示为:QR(w0)=Re[Q(iw0)],QI(w0)=Im[Q(iw0)]。可得
D(iw0,τ)=PR(w0)+iPI(w0)+[QR(w0)+
iQI(w0)][cos(w0τ)-isin(w0τ)]
(14)
若式(14)为零,那么实部和虚部分别为零。即
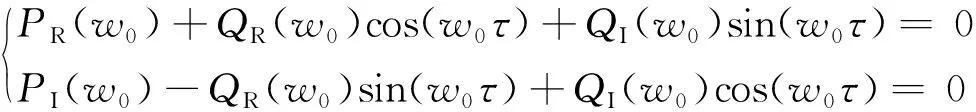
(15)
对式(15)进行联立求解,可得到一个不含时滞量τ的多项式,令F(w0)=PR(w0)2+PI(w0)2-[QR(w0)2+QI(w0)2],据此可得系统的判别多项式为
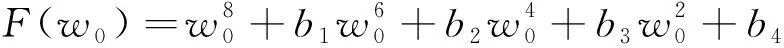
(16)
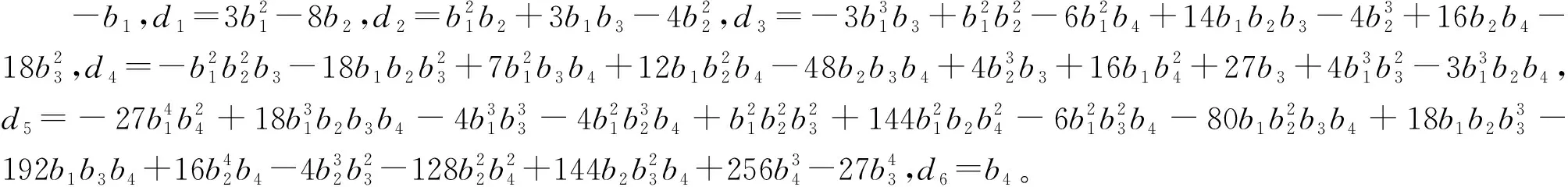
设l为判别式序列非零项数,k为判别式序列号符号变化数,则F(w)有l-2k个不同的实根。若l-2k=0,多项式F(w0)无实根,说明随时滞量增大,系统特征根不穿过虚轴,系统稳定性不会发生改变,此时系统的稳定性取决于无时滞时系统是否为渐进稳定。若l-2k>0,多项式F(w0)存在实根时,即参数落在全时滞稳定性区间以外,整个系统稳定性随时滞改变发生稳定性变化。由式(15)可以求得临界时滞为
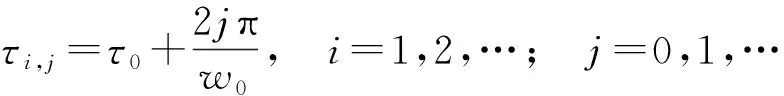
(17)
式(17)中:ω0为多项式F(ω0)的正实根;τ0为初始临界时滞;i表示多项式F(ω0)的第i个正实根ω0;j表示第j个临界时滞;τi,j表示第i个正实根对应的第j个临界时滞。
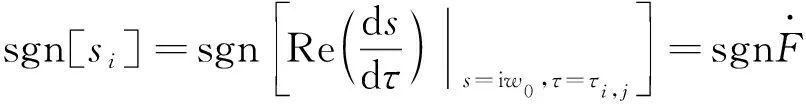
2.2 车身位移时滞反馈控制稳定性分析
根据式(3)建立车身位移时滞反馈系统控制方程,式(12)和式(13)确定系统特征方程和特征方程的多项式。利用时滞无关稳定性条件①在选定的参数范围内画出Routh-Hurwitz稳定性区域。然后将多项式(16)中的系数b1、b2、b3和b4代入Sturm判据,画出判别式序列系数dj=0(j=0,1,…,6),可以得到选取参数范围内的函数图像。取与Routh-Hurwitz稳定性区域的交集,可以得到稳定性区域,如图2所示。多项式F(w0)的判别式序列符号如表3所示。
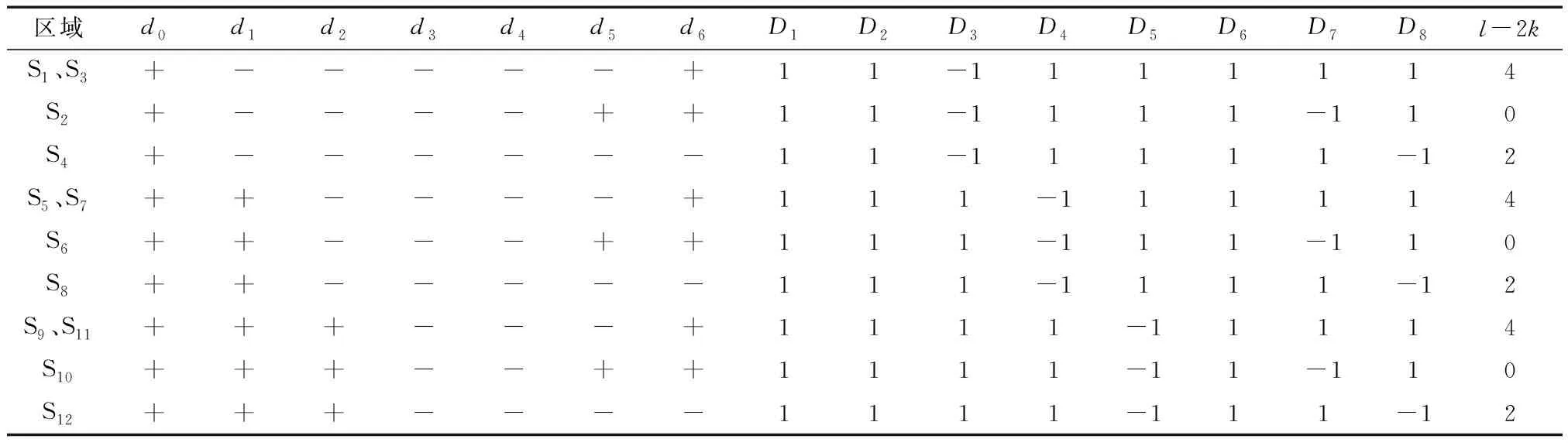
表3 车身位移时滞反馈判别式序列符号
参数范围被划分为15个部分。在S1、S3、S5、S7、 S9和S11区域,判别式序列非零项数为8,符号变化数为2,此时多项式存在2个互异的正实根。在S4、S8、S12区域,判别式序列非零项数为8,符号变化数为3,此时多项式存在1个正实根。S2、 S6、S10区域,判别式序列非零项数为8,符号变化数为4,多项式无实根。由上述分析可得,图2蓝色区域不符合时滞无关稳定性条件①,在τ=0时不满足Hurwitz稳定,此范围的参数使系统失稳;橙色区域存在实根,需要先确定临界时滞,根据稳定性切换方法来确定稳定性区间;绿色区域不存在实根,是时滞无关稳定性区域,不会随着时滞的增加发生稳定性切换。

图2 车身位移时滞反馈稳定性区域Fig.2 Stability region of vehicle body displacement feedback with time-delay
2.3 轮胎位移时滞反馈控制稳定性分析
对于含轮胎位移时滞反馈控制系统的稳定性,采用上述相同分析方法可以得到稳定性区域,如图3所示。以轮胎位移时滞反馈控制的多项式F(w0)判别式序列符号如表4所示。在选取的参数范围内都满足Routh-Hurwitz稳定。参数范围被划分为9个区域。图3中,在Z1、Z2和Z6区域,判别式序列非零项数为8,符号变化数为4,多项式无实根;Z3、Z4、Z5和Z7区域,判别式序列非零项数为8,符号变化数为2,此时多项式存在2个互异的正实根;Z8、Z9区域,判别式序列非零项数为8,符号变化数为0,此时多项式存在4个正实根;橙色区域存在实根,需要根据稳定性切换方法来确定稳定性区间;绿色区域是时滞无关稳定性区域,不会随着时滞的增加发生稳定性切换。
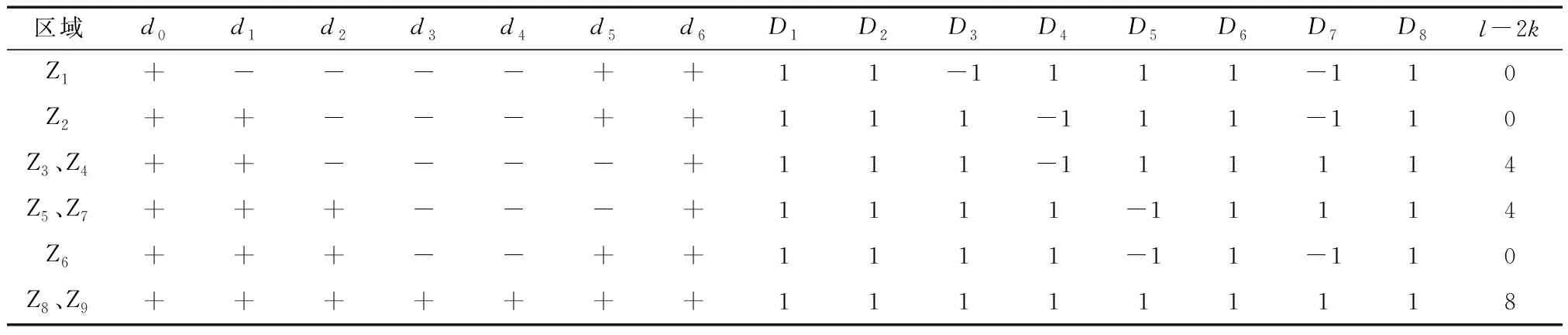
表4 轮胎位移时滞反馈判别式序列符号
3 时滞方程求解方法
将式(3)中的时滞项和第三项外界激励均看作激励项,则方程的解可表示为

(18)
式(18)中:x为状态变量节点。
对式(18)进行数值离散,令时间步长Δt=tk+1-tk,若仿真时长为T,则总步数时间步长n=T/Δt,可以得到每个步长为Δt的时刻,则式(18)可以化为
xk+1=exp(AΔt)xk+
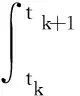
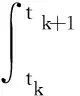
(19)
进一步可表示为
xk+1=exp(AΔt)xk+

(20)
通过求解方程可得每个时间节点的系统振动响应为

(21)
4 参数的优化及分析
4.1 目标函数的建立
在满足上述约束条件下,含时滞反馈控制的悬架系统优化目标要最大可能的降低车身的振动响应量。针对不同的外部激励,定义车身的加速度、速度和位移来评价不同位移时滞反馈控制对车身振动的影响。可得目标函数为
J=e1J1+e2J2+e3J3
(22)
式(22)中:J1为车身加速度的均方根值;J2为车身速度的均方根值;J3为车身位移的均方根值;e1、e2、e3为权重系数。
4.2 约束条件
为了保证含时滞反馈控制汽车的行驶安全性,除了要满足时滞稳定条件外,还必须要满足以下两个约束条件。
(1)为了保障车辆的行驶安全性,悬架动挠度在悬架限位块的范围内,即
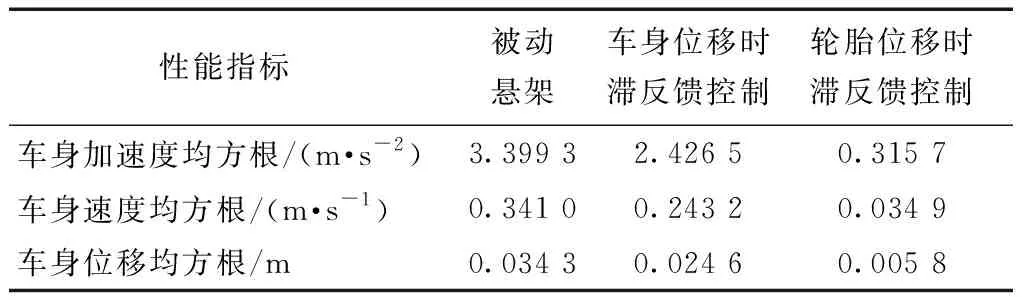
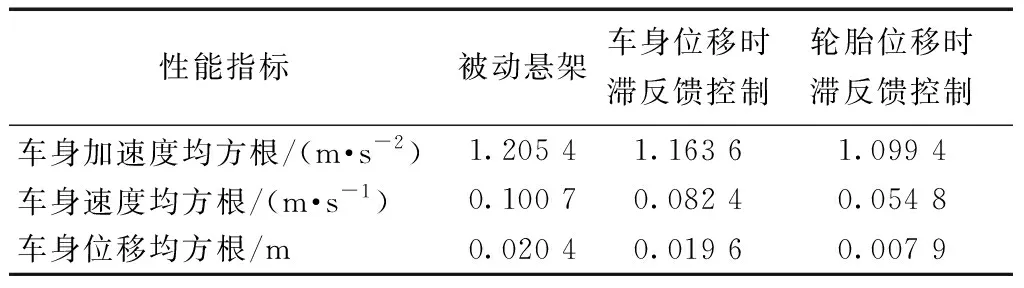
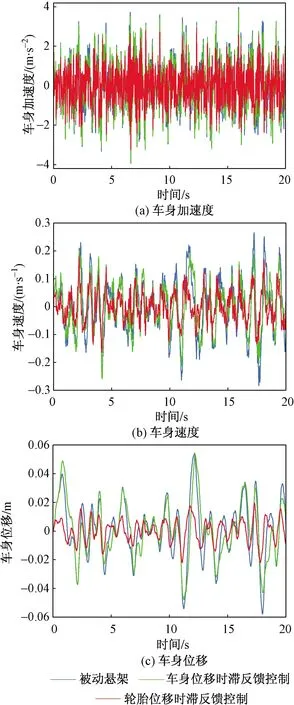
xs(ti)-xt(ti) (23) 式(23)中:xs(ti)为每个时间节点的车身位移;xt(ti)为每个时间节点的轮胎位移;xR为允许的最大悬架动挠度。 (2)为了保证车辆的路面附着性和操纵稳定性,时滞反馈控制系统下的轮胎动位移需要将轮胎动位移限定在一定范围内,即 (24) 式(24)中:xr(ti)每个时间节点的路面激励;xT为被动悬架轮胎动位移均方根值。 对目标函数进行优化分为以下7个步骤,流程如图4所示。 图4 优化程序流程图Fig.4 Flowchart of the optimization procedure 步骤1初始化优化算法参数,τn(n=s, t)∈[0,1],gn(n=s, t)∈[-30 000, 30 000]区域内,随机产生50个粒子,即种群数量。迭代次数N=200,最大速度为Vmax,初始位置为Xid,初始速度为Vid,惯性权重为wk,学习因子c1=1.2、c2=1.2。粒子在每个维度上的位置被限制在选定区域内,最大速度为每个维度搜索空间范围的某个分数。 步骤 2随机产生初始种群,并暂时记为群体最优,在群体内找到最优粒子记为全局最优。 步骤3对系统迭代次数进行记录,并将当前迭代次数与最大迭代次数进行比较。 步骤4在原有的群体基础上,通过粒子群算法更新群体位置进行迭代,可表示为 (25) 式(25)中:k为当前迭代次数;r1和r2为在[0,1]产生随机参数;Pid为个体最优粒子位置;Pgd为全局最优粒子位置;Vid为粒子飞行速度;Xid为粒子当前位置。 为提高算法的收敛性,采用变惯性权重。起始惯性权重wstart=0.9,终止惯性权重wend=0.4,当前惯性权重为 wk=wstart-k(wstart-wend)/N (26) 步骤5适应度函数,时滞悬架性能和稳定性由时滞量和反馈增益系数K=[gn,τn]所决定,通过优化这两个参数来得到车身能量的最小值,因此含时滞反馈控制的悬架目标优化设计问题可表示为 J(K)=e1J1+e2J2+e3J3 (27) 式(19)中:J为K的目标函数。 步骤6在步骤4更新的粒子位置代入步骤5中函数,计算获得新的自适应函数值。在迭代寻优过程中把每个粒子适应度值进行比较,保留产生较小自适应函数的粒子。 步骤7当循环次数达到所设定的迭代次数N时,系统输出优化后的最优参数。 在随机激励下,以车身位移时滞反馈得到系统的优化参数为τs=0.309 8 s,gs=-7 060 N/m。优化参数在图2的稳定性区域S6,属于全时滞稳定区域。以轮胎位移时滞反馈控制得到的系统优化参数τt=8.335 8×10-5s;gt=14 862 N/m处于图3的Z2区域,处于全时滞稳定区域,所以系统是稳定的。 将得到的优化参数代入式(3),在简谐激励xr=0.05sin(10t)的作用下,分别对车身和轮胎位移时滞状态反馈控制的主动悬架进行仿真。为评价时滞反馈控制对车身振动的影响,基于车身加速度、速度和位移为车身振动性能的评价指标。其仿真结果如图5所示,车身各项性能指标如表5所示。 表5 简谐激励下性能评价指标 由图5和表5可得,无论轮胎位移时滞反馈控制还是车身位移时滞反馈控制相对于被动悬架都对车身加速度、速度和位移均有明显衰减,基于车身位移时滞反馈控制的车身加速度、速度和位移均方根由3.399 3、0.341 0、0.034 3分别减小到2.426 5、0.243 2、0.024 6,减小比例分别为28.62%、28.68%、28.28%;基于轮胎位移时滞反馈控制的车身加速度、速度和位移在达到稳定状态下几乎可以为零,均方根分别减小到0.315 7、0.034 9、0.005 8,减小比例分别为90.71%、89.76%、83.09%。 图5 简谐激励下仿真对比Fig.5 Simulation comparison under harmonic excitation 简谐激励下含不同时滞状态反馈控制的主动悬架均对车身振动响应有所衰减,但含轮胎位移时滞反馈控制的主动悬架能极大地减小车身的振动加速度、速度和位移,有更好的车身减振效果,明显提升车辆乘坐舒适性;同时也能较大程度的改善车辆的行驶安全性和平顺性。 为进一步分析时滞反馈控制在主动悬架中的减振效果,建立随机路面模型。通常都是在频率上采用路面功率谱密度(power spectral density, PSD)描述其特性。根据《车辆振动输入 路面平度表示方法》(GB7031—1986),路面功率位移谱密度计算公式为 (28) 式(28)中:nspace为空间频率;n0为参考空间频率;Gxr(n0)为路面不平度系数;ω为频率指数;nmin和nmax分别为空间频率的下限和上限。 通过傅里叶变化将路面不平度分解为含不同频率和幅值的正弦波叠加。将空间频率变化到时间频率[20],根据给定的车速u,可以得到时间频率f=unspace,根据式(28)可得位移谱密度为 (29) (30) 式(30)中:θk为在区间[0,2π]上生成的随机数。 (31) 式(23)中:x为路面的长度。 根据式(23)模拟时域随机路面,设车速为20 m/s可得到路面随机激励时域图,如图6所示。 将优化出的参数代入式(3),在随机路面激励下进行仿真。随机激励下仿真对比如图7所示,各项性能评价指标如表6所示。由图7(a)可以看出, 表6 随机激励下性能评价指标 虽然车身位移时滞反馈控制可以减小车身加速度,但控制效果远不如轮胎位移时滞反馈控制。基于车身位移时滞反馈控制的悬架系统,车身加速度均方根由1.205 4减小到1.163 6,减小比例为3.47%。基于轮胎位移时滞反馈控制的悬架系统,车身加速度均方根由1.205 4减小到1.099 4,减小比例为8.79%。由图7(b)可知,轮胎位移时滞反馈控制明显优于车身位移时滞反馈控制下的车身速度响应,分别减小了45.58%、18.23%。由图7(c)、表6可知,轮胎位移时滞反馈控制和车身位移时滞反馈控制的位移响应比被动悬架分别减小了61.27%、3.51%。 图7 随机激励下仿真对比Fig.7 Simulation comparison under random excitation 随机激励下基于两种不同位移时滞反馈控制的悬架与被动悬架相比,轮胎位移时滞反馈控制的系统在车身加速度、速度和位移均方根值都有较大比例的减小,明显提升了车辆的乘坐舒适性。 对比分析了不同时滞反馈控制在1/4车辆模型对车辆的影响,通过仿真分析可以得出如下结论。 (1)针对1/4车辆模型建立含不同位移时滞反馈控制的主动悬架,利用Routh-Hurwitz判据和多项式判别定理分析了不同时滞反馈控制的稳定性区间。研究表明在车辆模型参数相同情况下,基于轮胎位移时滞反馈控制的主动悬架全时滞稳定性区域范围更广。 (2)在时滞反馈控制下,全时滞稳定区域与悬架阻尼有关,随悬架阻尼的增加全时滞稳定区域具有更大的范围。 (3)无论简谐激励还是随机激励下,轮胎位移时滞反馈控制比车身位移时滞反馈控制对车身有更好的减振效果。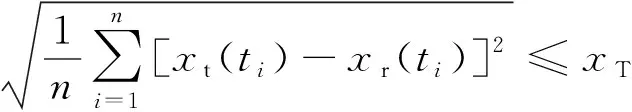
4.3 目标函数优化步骤
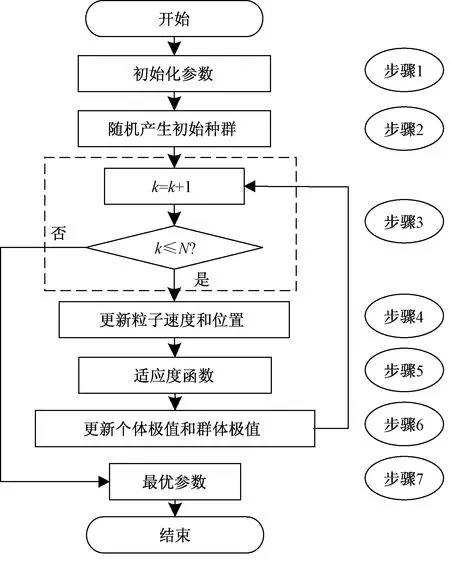
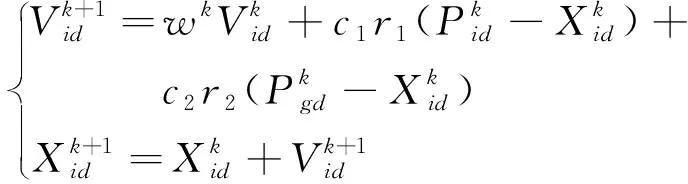
4.4 优化参数的稳定性分析
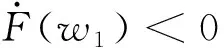
5 仿真分析
5.1 简谐激励仿真分析

5.2 随机激励仿真分析

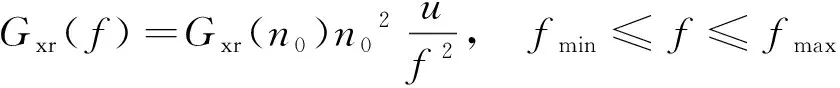
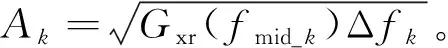
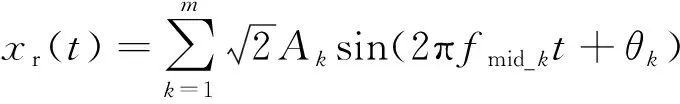
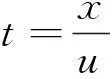

6 结论
