海南地区山体地形对地闪回击定位精度的影响

邹 斌， 崔海华， 张其林*， 李 静， 戴炳哲，姚年鹏， 蒋 尧， 杨 敢， 罗 华

(1.南京信息工程大学气象灾害教育部重点实验室， 南京 210044； 2.南京信息工程大学气候与环境变化国际合作 联合实验室， 南京 210044； 3.南京信息工程大学气象灾害预报预警与评估协同创新中心， 南京 210044； 4.南京信息工程大学中国气象局气溶胶与云降水重点开放实验室， 南京 210044； 5.河北省气象行政技术服务中心， 石家庄 050000)

雷电是一种常见的灾害性天气，每年造成大量的损失[1]。因此，对雷电进行深入的研究，提高闪电探测能力和定位精度，对降低雷电灾害损失，保障人类生产活动的有序进行和人员的生命财产安全具有积极的意义[2]。然而现实中除了引雷实验和极少数地方有引雷塔，可以对现实中雷电定位算法的定位误差进行评估，对于大部分的雷电很难得知其定位误差，而随着计算机技术的发展，模拟算法为评估雷电定位误差提供了有效途径。雷电电磁波在近地面传播过程中受土壤色散、土壤电导率以及高低起伏的不规则地形等因素的影响较大，会导致上升沿时间、电磁波波形峰值等发生改变，从而降低了雷击点的定位精度[3]。因此，利用二维时域有限差分法(finite difference time domain，FDTD)研究雷电电磁波传播特性并进行定位误差分析有重要意义。

在雷电回击电磁场的研究中，主要包括精确解析计算、近似计算和数值计算3种求解方法。Wait[4]利用等效表面阻抗定义的衰减函数，给出了垂直电场的近似计算公式。Cooray[5]和Rubinstein[6]给出了水平电场的近似计算公式。此后，经过学者们不断地改进，近似算法被不断推广，可以应用到分层土壤、粗糙地表和海陆交接等多种地形环境中[7-10]。然而，解析法在山体等非规则地形中的电磁场计算仍受到较多限制。

中外学者已利用FDTD算法，围绕土壤电导率[11]、土壤各向异性[12-13]、土壤色散效应[14]和地形[15-16]等多个因素进行了大量的分析讨论。张明霞等[17]利用矩量法，讨论了矩形山体模型对电磁辐射磁场的影响。Li等[18]在研究地形对雷电定位的影响中发现当传播路径中有锥形山体存在时，发现电磁场波形和峰值均会受到严重影响，并且信号的时延随山体高度的增加而增大，随地面电导率的减小而减小。Li 等[19]通过结合雷击山顶铁塔的实测电场波形和FDTD数值模拟，讨论了真实不平坦地形的影响，证实了山体地形对电场(15 km观测点)具有增强作用，结果表明忽略地形起伏的平地假设导致对反演估算的雷电流幅值达到真实值的1.8倍。陶玉郎等[20]利用3D数值模拟研究发现土壤的特征对雷电流冲击有很大影响。Hou等[21]建立2D FDTD锥形山体模型比较了0.3～50 km处电磁场的变化规律，发现对于垂直电场，近距离受山体的屏蔽作用影响被削弱，而远距离处的幅值则由于山脚的反射而增强。张金波等[22]利用2D FDTD算法对土壤电导率进行研究，结果表明山体地形坡度对雷电过电压有显著影响，尤其在土壤电导率为有限值的情况下，过电压幅值随地形坡度的升高而明显增大。

总的来说，以上研究大部分都局限在孤立山体，涉及实际山体地形的雷电电磁波传播特性较少。雷电电磁场沿复杂起伏地形传播时，会以绕射和反射的方式经过山体，会引起电磁场到达测站时间的增加，另外电磁场也会出现强度的变化，从而使根据雷电电磁场波形进行的闪电定位产生误差。因此如何将地形地貌带来的误差进行修正，提高闪电的探测效率和定位精度，是个亟需解决的问题。

为此，在二维柱坐标系下FDTD模型加入了真实地形，研究了真实地形对切向磁场波形以及闪电定位的影响。针对现有的TOA(time of arrival)时差定位算法的缺陷，即忽略了地形对电磁波的到达时间延迟作用，提出了不同步长的地形包络法，对定位精度进行优化。

1 研究内容和方法

1.1 测站和雷击点位置

海南地区位于中国南端，主要以山地为主，地势起伏比较严重，山地面积较大，纬度低四面环海，雷暴活动相对比较频繁，是中国雷电灾害最为严重的省份之一。以实际安装在海南省的7个测站位置为基础，将它们应用于FDTD模式中，7个测站分别为琼中站、乐东站、三亚站、昌江站、万宁站、文昌站、澄迈站，具体测站位置如表1所示。在闪电探测网区域选取了3个雷击点L1、L2、L3，具体位置如表2所示。

表1 测站坐标Table 1 Station coordinates

表2 雷击点坐标Table 2 Lightning coordinates

图1为海南地区测站和雷击点位置，在闪电探测网区域选取了3个雷击点L1、L2、L3,其中雷击点L1在中间山地区域，雷击点L2在东北平原地区，雷击点L3在西南山地附近的盆地区域，选取这3个雷击点具有代表性。

1.2 FDTD模式简介

FDTD是由麦克斯韦旋度方程的微分方程出发的，通过二阶中心差分方法，把原来的偏微分方程运算形式转换成差分方程，从而在一定的时间上和一定体积内，对连续的电磁场数据可以进行抽样压缩。

Maxwell方程组的旋度方程组形式为

(1)

式(1)中：E为电场强度；H为磁场强度；D为电位移矢量；ρ为电荷密度；B为磁感应强度；ε为电介质常数；σ为电导率；μ为磁导系数；t为时间。直角坐标系中，式(1)可表示为

(2)

式(2)中：x、y、z分别为直角坐标系的3个方向。

采用磁场波形进行闪电定位，则切向磁场的表达式为[23]

(3)

式(3)中：Δta为时间步长；Δr为水平方向网格长度；Δz为竖直方向格点长度；i为水平方向格点数；j为竖直方向格点数；Hφ为切向磁场；Ez为垂直电场；Er为水平电场；n为第n个计算单元；μ0为真空中的磁导率(即真空中的磁导系数)。

图2为FDTD模式示意图，模式中网格宽度Δr×Δz=10 m×10 m，满足数值稳定性条件，同时也与插值后的地形网格数据相匹配。时间步长Δt=16.7 ns，符合Courant稳定性条件。土壤电导率σg=0.001 S/m，相对介电常数εr=10。空气电导率σair=0 S/m，相对介电常数εr=1。边界采用卷积完全匹配层(convolution perfectly matched layer，CPML)吸收边界条件。闪电回击通道放置于计算区域的最左侧山顶的上面，通道高度H=7 500 m。

z为垂直方向；φ为切向；r为水平方向图2 模型示意图Fig.2 Model diagram

1.3 地闪回击模型

采用MTLE(modified transmission line)源回击模型，即回击通道中的回击电流以指数的形式沿着通道高度在衰减，回击通道中t时刻在高度z′处的电流分布可表示为

i(z′,t)=e-z′/λi(0,t-z′/ν)

(4)

式(4)中：e-z′/λ为数值衰减系数；i为电流强度；z′为高度；λ为衰减因子，取2 000 m；ν为回击速度，取1.5×108m/s。

使用Heidler双指数函数[24]来模拟继后回击下雷电流通道底部的基电流，如式(5)所示。典型的继后回击的电流参数如表3所示。

表3 继后回击电流参数典型值Table 3 Typical value of subsequent return stroke current parameters

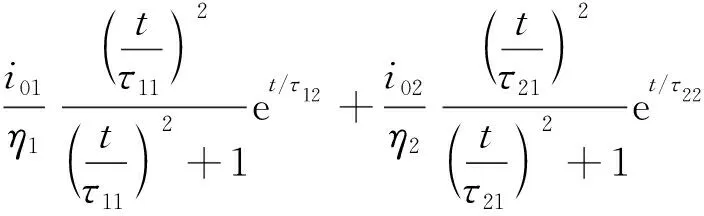
(5)

(6)

(7)

式中：i01和i02分别为击穿电流和电晕电流峰值；η1、η2分别为击穿电流和电晕电流峰值的修正因子；τ11和τ21分别为击穿电流和电晕电流的波形上升时间；τ12和τ22分别为击穿电流和电晕电流的波形下降时间。

1.4 波形到达时间计算方法

时差法是利用电磁信号到达不同测站的时间差进行定位，结合高精度的全球定位系统(global positioning system，GPS)同步时间测量，能够实现对辐射源点的准确定位。在利用TOA 算法计算辐射原点的过程中，首先对信号进行波形识别筛选出不同类型的闪电事件，同时对不同的同步脉冲进行分组，再计算出同步信号到达不同测站的时间差，然后假定信号沿直线距离以光速向测站传播，求解非线性方程组获得辐射源点位置的初值，并借助非线性最小二乘拟合算法对初解进行优化，最终得到辐射源点的位置。图3为到达时间示意图。

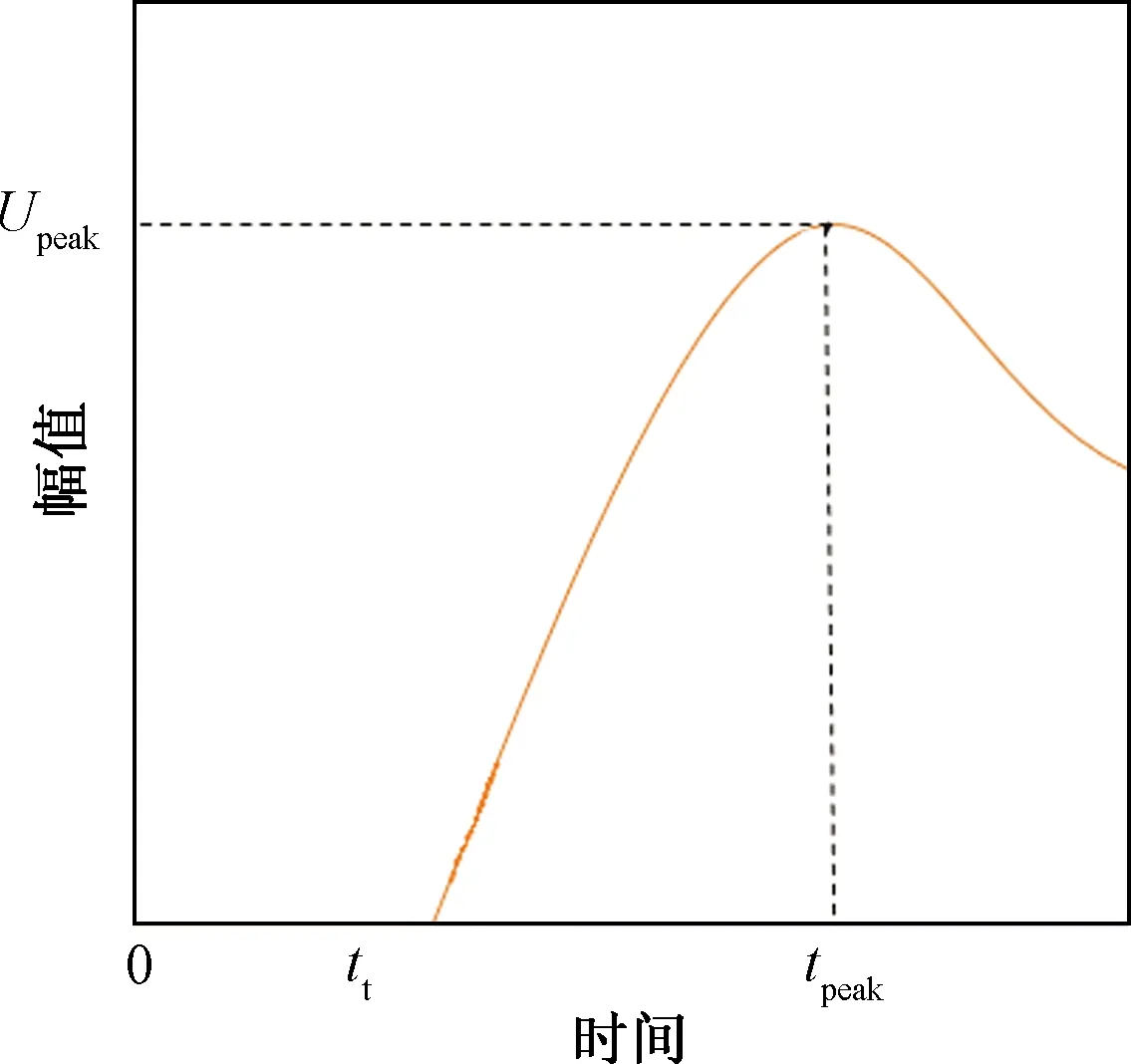
Upeak为闪电峰值电压；tt为闪电上升沿开始时间； tpeak为波形峰值时间，即逐峰法定义的时间图3 到达时间示意图Fig.3 Diagram of arrival time

为了求解出地闪回击点的空间坐标，需要先得到信号到达不同测站的时间差。在时间差的计算中，可以通过互相关方法直接计算出两两测站之间的时间差，也可以以电磁波峰值的到达时间为准，先计算出单站信号的到达时间，再与参考站点的到达时间相减获得两个测站之间的时间差。不同方法计算得到时间差可能存在一定的差异，为了对比不同方法的定位效果，选取互相关，逐峰法这2种方法的定位结果进行比较。

1.5 地形包络法

虽然对闪电定位普遍采用的是TOA时差法，但显然这种算法并没有考虑实际地形对闪电电磁波产生的路径延长问题，即信号到达每个测站的时间都会比理想情况下略长，因此采用不同步长的地形包络法来近似估计地形引起的延长时间。

如图4所示，地形包络即用连续线段将地形包围起来。考虑到所有测站和雷击点的距离大小，每隔5、10、20、40 km步长距离取每段地形的最高点并连线形成包络线。将这些地形包络线长度作为电磁波在传播中的近似传播距离，反映出信号传播路径随山体高度的变化。然后用包络线长度减去水平距离后除以电磁波的传播速度作为电磁波到达时间的误差订正值。假设真实路径下用包络法得到测站至雷击点路径长度为l1，水平路径为l2，可以得到误差订正时间Δtb的计算公式为

(8)

式(8)中：c为光速。

将原各个测站的信号到达时间分别减去对应的误差订正时间，重新进行雷击点定位。

1.6 时间补偿法

忽略测站GPS 计时精度的误差，信号从雷击点向测站传播的时间t，会因为地形、电导率等的影响而变化，与同等水平传播距离的理想平坦地表时的传播时间t存在一定的偏差，即

t=tflat+Δtc

(9)

式(9)中：tflat为信号以光速传播过平坦地表的时间；Δtc为真实崎岖地形情况与理想平坦地表情况的传播时间偏差。

进行时间补偿时，将信号以光速沿红色折线和黑色直线传播的时间差作为对式(8)中Δt的估算，减少传播时间t与理想情况下的tflat的偏差。有必要时，考虑进行多次补偿，提高最终定位结果的准确性。

1.7 雷击点到测站真实地形

图5～图7为L1、L2、L3雷击点到测站的真实地形高程图，可以看出，雷击点L1雷电电磁波传播路径的总体趋势为由高到低，雷击点在山地上，传播路径总体上比较复杂，地形起伏较大；雷击点L2在平原地区，传播的总体趋势为由低到高，总体上受山地影响较小；雷击点L3在万宁测站附近，雷击点海拔高度低，但其四周地势都比雷击点高，在山地的低洼区域，受山地影响更明显。

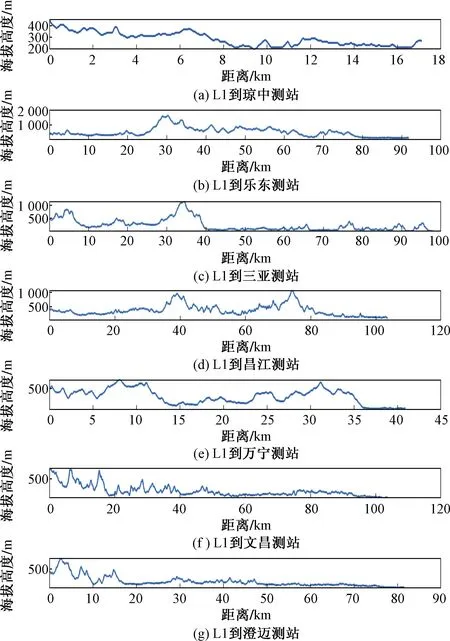
图5 雷击点L1到测站地形图Fig.5 Topographic map of lightning L1 to the station

图7 雷击点L3到测站地形图Fig.7 Topographic map of lightning L3 to the station

2 模拟结果与讨论

2.1 平地与真实的波形对比

图8～图10为雷击点L1、L2、L3到每个测站平地与真实地形的波形对比。蓝色线和红色线分别为平地和真实地形的模拟结果。山地地形对波形的上升沿时间和波形峰值影响较大。上升沿时间增加范围在1～5 μs，主要是电磁波在传播中受土壤有限电导率和色散效应影响，高频电磁场存在更大的衰减。同样峰值时间也都是滞后于平地的，但峰值的大小变化却不尽相同。

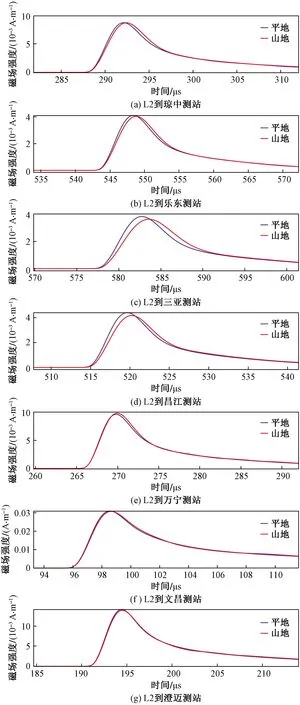
图9 雷击点L2到测站磁场波形Fig.9 Magnetic field waveform from lightning L2 to the station

图10 雷击点L3到测站磁场波形Fig.10 Magnetic field waveform from lightning L3 to the station

对于雷击点L1，琼中站真实地形下峰值明显比平地情况大很多，峰值时间较平地情况也提前，而其他6个测站真实地形下的峰值对比与平地都略有减少，真实地形下峰值时间明显滞后于平地传播的峰值，这主要受山地影响，雷电高频电磁波衰减较大，而琼中站距雷击点距离较近，受山地影响较小，这也说明了地形对电磁波影响的复杂性。

对于雷击点L2，7个测站真实地形下的峰值都略小于平地情况，峰值时间也都滞后，三亚站和昌江站滞后比较明显，峰值减小也较明显，其他5个测站真实地形下的电磁波波形及到达时间基本上一致，这主要受传播路径影响，闪电从雷击点L2到三亚站和昌江站受山地影响较大，而从雷击点L2到另外5个测站地形相对比较平坦。

对于雷击点L3, 6个测站真实地形下的峰值都明显小于平地情况，峰值时间除乐东站外也都明显滞后，主要是乐东站从雷击点L3到测站传播路径比较平坦，和雷击点L2一致。

2.2 真实地形下滤波前后波形对比

考虑到雷电探测传感器探测都具有特定的带宽，实际接收的波形已被过滤。在此，使用带通滤波器，对2-D FDTD模型的模拟磁场波形进行过滤，以分析带宽对雷电磁场的影响。图11～图13分别为雷击点 L1～L3 在真实地形下，各测站接收的磁场波形过滤前后对比，频率范围为10～500 kHz。与过滤前相比，磁场峰值减小，波形变陡，上升沿时间变短，而峰值到达时间与过滤前相比几乎相等，这样对于逐峰法定位来说，误差几乎相似。

图11 雷击点L1真实地形下到测站滤波前后磁场波形Fig.11 Waveforms of magnetic field before and after filtering at lightning point L1 in real terrain

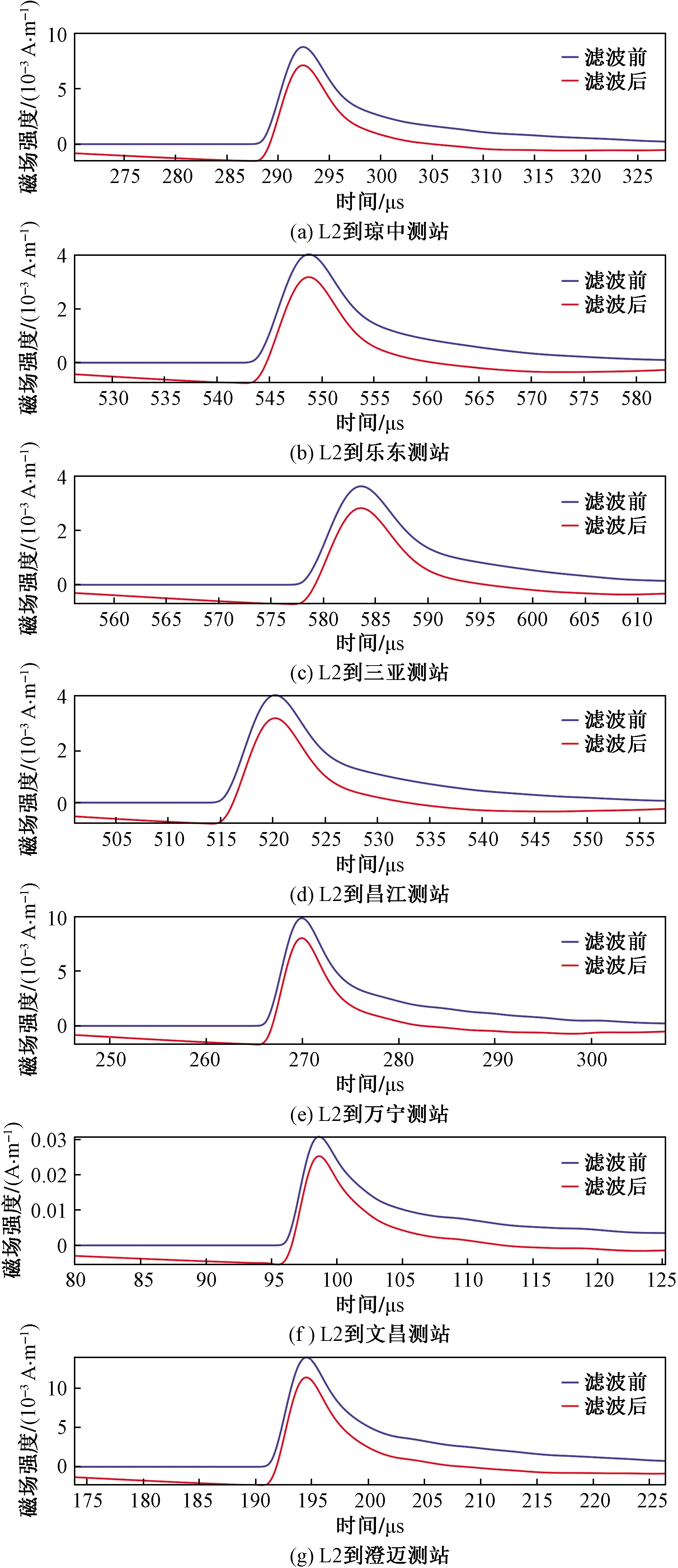
图12 雷击点L2真实地形下到测站滤波前后磁场波形Fig.12 Waveforms of magnetic field before and after filtering at lightning point L2 in real terrain

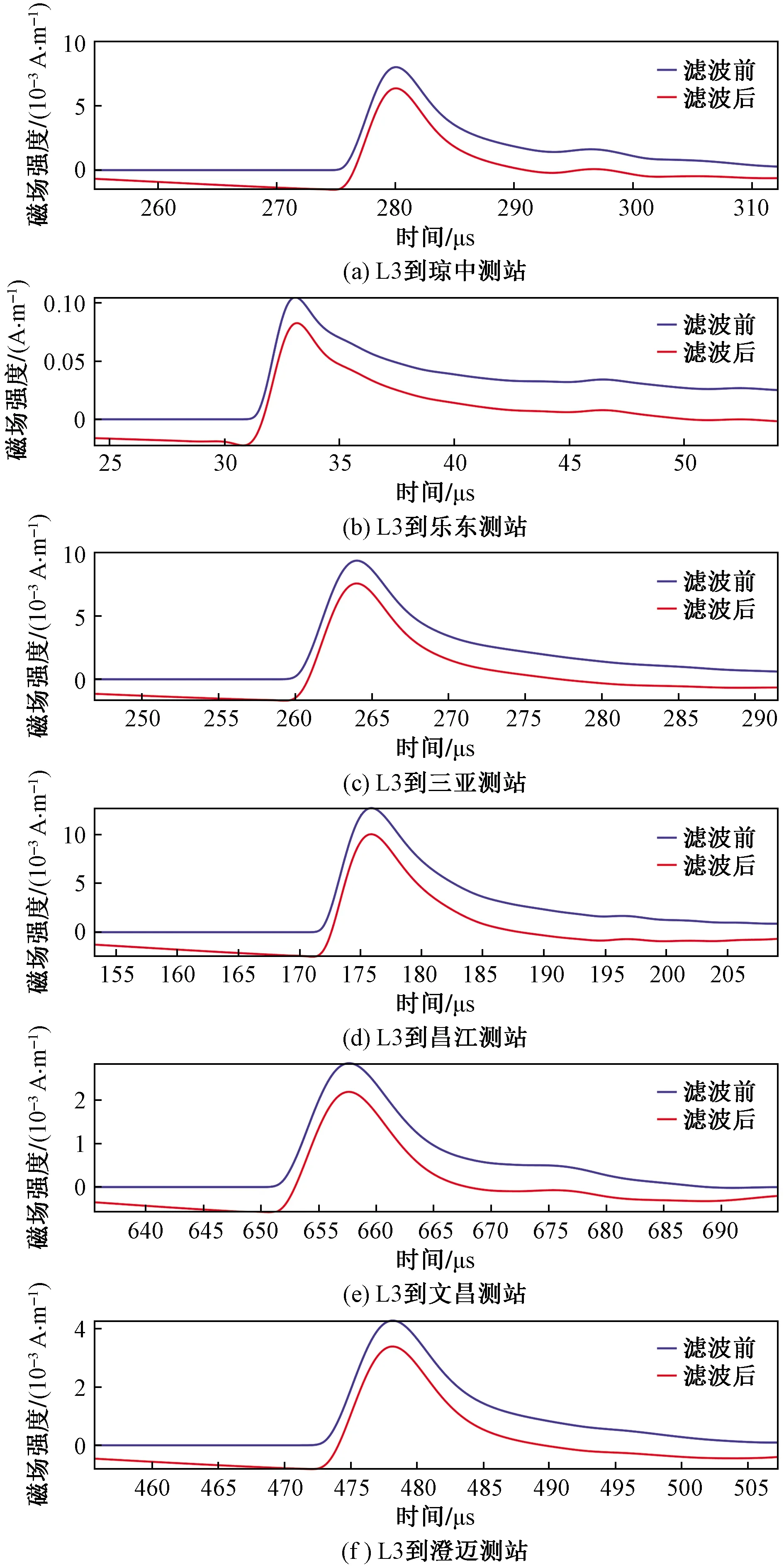
图13 雷击点L3真实地形下到测站滤波前后磁场波形Fig.13 Waveforms of magnetic field before and after filtering at lightning point L3 in real terrain

2.3 定位点的偏差及修正

图14为在逐峰法波形到达时间算法下3个雷击点在平地、真实地形、以及不同步长地形包络法修正后的定位误差对比图。可以看出，雷击点L2的误差较小，主要是雷击点L2到测站的传播受地形影响较小，且用包络法进行修正，随着包络空间步长的增加，定位误差在减小；对于雷击点L1和L3，定位误差明显大于雷击点L2的定位误差，对于平坦地表，定位误差只有十几米，定位效果较好，而使用包络法和时间补偿法进行修正，定位误差明显减小，且包络空间步长越小，定位误差越小。

图14 逐峰法定位误差Fig.14 Location error by peak method

图15为在互相关法波形到达时间算法下3个雷击点在平地、真实地形、以及不同步长地形包络法修正后的定位误差对比。可以看出，雷击点L1的定位误差相比较其他两个雷击点要小很多，雷击点L3使用六站进行定位相比较雷击点L1的7站定位，定位误差明显大了很多；对于3个雷击点，使用包络法和时间补偿法进行修正，定位误差明显减小，且包络空间步长越小，定位误差越小。

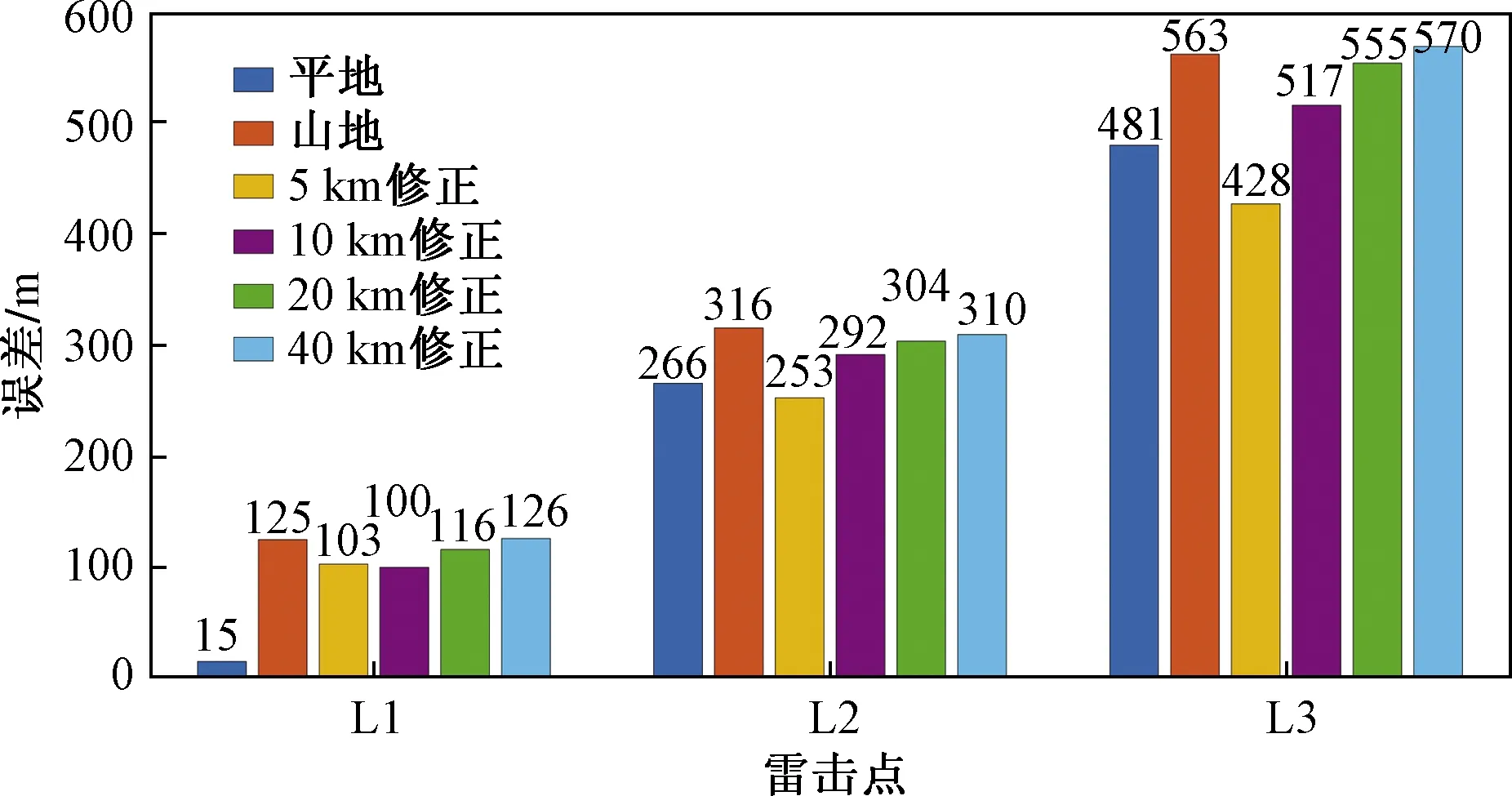
图15 互相关法定位误差Fig.15 Location error by cross-correlation method

对比3个雷击点在两种定位算法下的定位误差，从图14、图15可以看出：对于平坦地表，雷击点逐峰法下的定位效果更好，定位误差都只有几十米，而对于雷击点L1，因为传播受地形影响较大，使用互相关算法定位误差较好，而雷击点L2、L3，因为传播路径都相对来说比较平坦，使用逐峰法定位效果较好，因此，在实际的闪电定位中，因为测站接收电磁波受各种因素影响，使用互相关效果应该更好。

3 结论

(1)山地地形会明显改变切向磁场的波形峰值大小和上升沿时间，相比较平地，切向磁场波形峰值变化最大的减小了38%，上升沿时间增加范围在1～3 μs，峰值到达时间也滞后于平地情况，而经过带通滤波器进行滤波处理，与过滤前相比，磁场峰值减小，波形变陡，上升沿时间变短，峰值到达时间与过滤前相比几乎相等不变。

(2)对于逐峰法，雷击点在真实地形路径下定位误差分别为351、31、261 m，相比平地明显增大很多；而对于互相关算法，3个点的定位误差明显比逐峰法大很多，真实地形路径下定位误差比平地情况下大，但差距明显有所减小。

(3)使用一种可以修正闪电定位误差的算法，即不同空间步长的地形包络和时间补偿法，在一定程度上减少地形带来的闪电定位误差。在考虑海南地区的实际地形情况下，雷击点L3最大修正了135 m，且不同空间步长在相同地形包络法下修正效果不同。对于逐峰法，闪电L1和L3使用5 km步长的包络修订较好，而闪电L2使用40 km步长的包络修订效果较好，因为闪电L1和L3传播受地形影响较大；使用互相关法，闪电L1使用10 km包络修订效果较好，而闪电L2和L3使用5 km包络修订效果较好，定位误差都在百米量级内，相比较其他算法闪电定位精度有很大提高。