基于能量密度因子法的复杂环境下爆炸冲击波超压峰值解析计算
2021-10-20寿列枫
钟 巍, 田 宙, 寿列枫,3
(1.西北核技术研究所, 西安 710024; 2.北京大学数学科学学院, 北京 100871; 3.北京理工大学爆炸科学与技术国家重点实验室, 北京 100081)
近几十年来,复杂城市环境和地下空间等的爆炸冲击波传播和毁伤研究受到学者们极大的重视[1-6],这实际上是爆炸冲击波在复杂几何布局条件下的传播问题[7-9],为此,学者们通常将城市环境或地下空间等简化为各种复杂的几何布局进行研究,如长直坑道、十字坑道等[10-11],针对这类问题主要采用数值模拟[12-16]和实验方法[10, 17-19],解析方法研究主要集中在自由场爆炸冲击波传播方面[20-25],对于简单的坑道模型有学者基于数值模拟和实验数据通过数据拟合得到了解析计算公式[26]。何翔等[27-28]评估了砖隔墙毁伤后的冲击波破坏效应,对有无砖隔墙空气冲击波实测波形进行了分析,得到了合理设置砖隔墙有利于提高防爆性能的结论。骆浩浩等[29]开展了井下爆破直通巷道冲击波超压的预测研究,给出了超压峰值预测公式适用于预测井下直通巷道的冲击波超压峰值。孙中博等[30]开展了竖井横通道爆炸冲击波传播规律的试验研究,分析了竖井横通道炸药爆炸试验的实测冲击波数据特征,对于研究受限空间内爆炸冲击波的传播规律具有借鉴意义。邓照玉[31]采用数值模拟手段对瓦斯爆炸对巷道壁面损伤破坏情况进行了研究,结果表明整体超压峰值在巷道内会出现振荡波动,并且瓦斯区壁面承受的载荷最大,研究结果可为优化巷道结构的设计提供参考。万宇等[32]利用机器学习和特征优化算法提出了信息增益与支持向量机的组合模型预测瓦斯爆炸的风险,其正确率高于其他预测模型,证明了其优越性。
在许多工程实际应用中,常常需要快速估算某些复杂几何布局条件下的爆炸冲击波参数,甚至可以适当降低对计算精度的要求,而数值模拟从几何建模、网格划分、数值计算到结果后处理等常常需要花费大量的时间,实验研究周期更长且需要更大的经济和人力成本。此时,对复杂几何条件下爆炸冲击波参数的解析计算具有重要意义。
为此,基于量纲分析和Taylor展开,将对空中爆炸自由场冲击波超压峰值计算公式进行严格的推导,基于推导过程引入能量密度因子方法,将自由场冲击波超压峰值计算公式推广到复杂几何布局情形。最后通过与刚性地面爆炸冲击波超压峰值计算经验公式、两端开放无限长坑道爆炸冲击波超压峰值实验结果比较,对所推导的解析计算公式进行验证。
1 自由场超压峰值解析公式推导
1.1 超压峰值计算公式
关于确定爆炸冲击波参数不同学者开展了大量研究工作,得到了大量的解析计算公式、图表[21, 23,33-36],这些公式或者图表主要是基于对各种各样的实验数据的分析获得的。在处理实验数据时,通常采用的方法是将冲击波参数表示为比例距离的函数,比例距离定义为
(1)
式(1)中:R为爆心距离,m,量纲为L;W为等效TNT爆炸当量,kg,量纲为M。
(1)Brode[33-34]冲击波超压峰值表达式为
(2)
式(2)中:Δp为超压峰值, MPa,量纲为ML-1T-2。
(2)Henrych[35]冲击波超压峰值表达式为
(3)
(3)Naumyenko等[36]冲击波超压峰值表达式为
(4)
(4)张守中[37]冲击波超压峰值表达式为
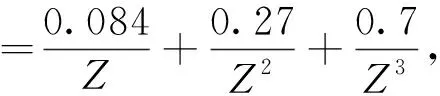
1 m/kg1/3≤Z≤15 m/kg1/3
(5)
1.2 基于量纲分析和Taylor展开的公式推导
观察冲击波超压峰值计算公式[式(2)~式(5)]可知,式(2)~式(5)都是关于比例爆心距离Z的倒数的多项式函数,不同之处在于各个公式的适用范围和多项式系数不相同。基于量纲分析和Taylor展开对冲击波超压峰值计算公式进行推导,并利用推导过程解释上述现象。
1.2.1 基于量纲分析推导定性函数表达式
将自由场爆炸近似看作是点爆炸,则爆炸后会产生向外扩展的球形冲击波,决定冲击波强度特征的参量主要来自以下三个方面。
(1)炸药属性:W为等效TNT爆炸当量,kg;ρe为装药密度,kg/m3,量纲为ML-3;单位质量炸药爆炸释放的能量为Ee,J/kg,量纲为L2T-2;爆炸产物的膨胀指数为γe,SI,量纲为S。
(2)空气属性:pa为初始压力,Pa,量纲为ML-1T-2;初始密度ρa,kg/m3,量纲为ML-3;绝热指数γa,SI,量纲为SI。
(3)爆心距离:R为爆心距离,m,量纲为 L;用冲击波超压峰值Δp来表征冲击波的强度,则可表示为物理量的函数:
Δp=Ψ(W,ρe,Ee,γe;pa,ρa,γa;R)
(6)
式(6)涉及的物理量总数为9个,共有3个基本量,分别为质量、长度、时间,对应的基本量纲为M、L、T。因此,根据定理[38]可知。式(6)可表示为6个无量纲量的函数形式。通过量纲分析[39],可以得到这6个无量纲量为
(7)
则可得无量纲函数关系式为
(8)
对于一般空气条件下同种类型炸药爆炸,存在
(ρe,Ee,γe;pa,ρa,γe)=const
(9)
式(9)中:const为常数。
去掉无量纲常量后,式(8)可化简为
(10)
在约定好单位后,可以继续去掉式(10)中的常量,即式(10)可以进一步简化为
(11)
式(11)表明,自由场空气爆炸冲击波超压峰值可以表示为比例距离的函数关系式。
1.2.2 利用Taylor展开得到多项式形式函数表达式
爆心距离越大,超压峰值越小;爆炸当量越大,超压峰值越大,即“超压峰值与爆心距离成反比,与爆炸当量成正比”。为了体现这一物理性质,记
(12)
将式(11)改写为
(13)
从大量的实验数据[40]观测到自由场空气中爆炸冲击波超压峰值随比例距离的衰减规律,如图1所示。
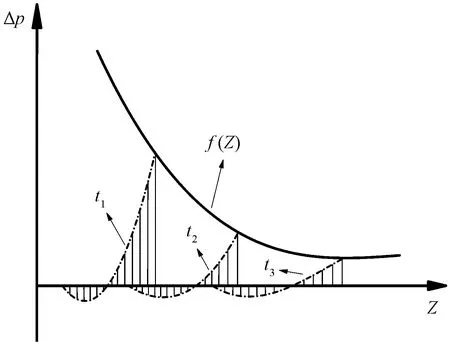
t1、t2、t3表示3个不同时刻图1 自由场爆炸冲击波超压峰值曲线Fig.1 The overpressure-time curve of free-field explosion
根据图1,假设函数f(Z)是充分光滑的,即在数学上假设f(Z)∈C∞(Z),其中C∞(Z)表示在定义域Z上足够光滑,则在Z∈(0,+∞)区间内关于w的函数g(ω)满足g(ω)∈C∞(ω),对式(13)作Taylor展开得

hk(ω0)(Δω)n+1
(14)
式(14)中:Δω=ω-ω0;ω0=1/Z0,其中Z0为指定值,余项为高阶项。因此,可以忽略式(14)中的高阶小量,化简为
(15)
式(15)中:g(k)(ω0)表示在ω0处的k阶导数。进一步可将式(15)写为
(16)
式(16)中:χi为常系数,i=0,1,…,N为足够大的正整数。
于是式(16)给出了自由场空气中爆炸冲击波超压峰值关于比例距离的多项式函数关系式。显然,式(2)~式(5)均满足式(16)的形式。正如式(2)~式(5)所表现出来的一样,截至目前,尚未有学者从理论上提出式(16)中常系数χi(i=0,1,…,N)的计算方法,因此,工程上学者们通常是基于式(16)的形成利用实验结果进行数据拟合得到一定范围内的系数χi(i=0,1,…,N),而由于实验受到各种条件的影响,每个研究者所掌握的实验结果存在差异,从而拟合出的系数也差别较大,这也是目前存在许多不同自由场空气中爆炸冲击波超压峰值计算公式的原因。
2 能量密度因子方法与自由场爆炸冲 击波超压峰值解析计算公式的推广
2.1 方法描述
式(16)是通过量纲分析和Taylor展开得到的,而量纲分析的结果是物理本质的体现,Taylor展开属于严密的数学处理,即式(16)是符合物理规律的。进一步考虑式(16)中的无量纲变量Z,从能量的角度来考虑它的定义[式(1)],容易发现无量纲变量Z本质上反映的是体积能量密度,即爆炸冲击波超压峰值是关于体积能量密度的形如式(16)所示的多项式函数。因此,如果体积能量密度相同,则按式(16)计算得到的超压峰值相等。
基于上述原理,对于非自由场空气中的爆炸,如复杂几何布局条件下的爆炸等,可以通过某种合理的方法转换为体积能量密度相等的自由场空气中爆炸,然后使用已有的自由场空气中爆炸冲击波超压峰值计算公式进行计算,而这种合理的转换方法即为这里所提的能量密度因子方法。
如图2所示,以一端封闭一端开放坑道内爆炸为例给出能量密度因子的定义。已知爆炸TNT当量为W,假设图2中T点处的超压达到峰值时爆炸冲击波扩散到的空间为图2中灰色圆柱体区域,该区域显然不是自由空间,而是一端开放一端封闭的约束空间,这里仍称为坑道(实际上只是坑道的一段)。记该坑道体积为V,则T处的体积能量密度为

图2 一端封闭一端开放坑道内爆炸示意图Fig.2 Sketch map of explosion for the one closed-end tunnel
(17)
以爆心为球心,以爆心到T点的距离R为半径作一个球体,若在球心处以W*为TNT当量发生的自由空间爆炸冲击波传播到T点时的体积能量密度也为ωT,则按式(16)计算得到的自由场空气中以W*为TNT当量爆炸距离R处的超压峰值即为所要求的坑道中T点的超压峰值。于是,主要问题是求出W*。
显然,对于等效的自由场爆炸易得其体积能量密度为
(18)
由式(17)、式(18)可得
(19)
(20)
VECF是从空间体积的影响这个角度考虑的,将这种思路推广到能量密度因子(energy concentration factor,ECF),则还可以将其他影响因素考虑进来。如考虑介质特性的影响,显然对于地面爆炸绝对刚性地面(地面是钢板、混凝土、硬岩等情况)和非绝对刚性地面(地面是沙、黏土、软岩等情况)对爆炸能量的吸收和反射是不一样的,经过相关处理,这种差别也可以体现到能量密度中去,从而得到对应这种处理的ECF;又如可以从面积能量密度的角度提出面能量密度因子(surface energy concentration factor,SECF),可表示为
(21)
式(21)中:SSph为等效球体的球面面积,SSph=4πR2;S为实际情况下爆炸冲击波与静止空气接触界面的表面积。文献[36]中给出的坑道内爆炸冲击波超压峰值计算公式本质上是利用面能量密度因子方法所得。
尽管上述面能量密度因子在工程应用上来讲不会有大的问题,但结合第1节推导过程可以发现,按式(20)定义的体能量密度因子是完全符合物理本质的,也应该更符合实际物理现象,这一点将在后文的算例分析中得到验证。因此,采用体能量密度因子。
将式(19)代入式(16)即得基于自由场公式推广的冲击波超压峰值解析计算公式,可表示为
(22)
式(22)中:Z*为等效比例距离。
(23)
式(23)中:W为实际TNT爆炸当量;R为实际的爆心距离;VECF为体能量密度因子。
2.2 几种典型几何布局的能量密度因子
比较常见复杂几何布局条件下的体能量密度因子和面能量密度因子。同样,假设示意图(图3、图4)中T点处的超压达到峰值时爆炸冲击波扩散到的空间为图3、图4中灰色区域,同样的,这些区域显然不是自由空间。
(1)刚性地面爆炸,如图3所示。

图3 刚性地面爆炸示意图Fig.3 Sketch map for the rigid ground explosion
(24)
(25)
(2)两端开放通道爆炸,如图4所示。

图4 两端开放通道爆炸示意图Fig.4 Sketch map for the two open-end tunnel explosion
(26)
(27)
式中:VTun_Open为开放坑道的体积;STun_Open为坑道开放端与空气接触表面的面积。
(3)一端封闭一端开放通道爆炸,如图2所示。
(28)
(29)
式中:VTun_Close-end为一端封闭一端开放坑道的体积;STun_Close-end为该坑道开放端与空气接触表面的面积。
(4)圆柱形截面十字通道爆炸,如图5所示。
(30)
(31)
式中:VTun_Crossed为十字交叉坑道的体积;STun_Crossed为该坑道开放端与空气接触表面的总面积。
(5)四周开放的两刚性夹层间爆炸,如图6所示,两刚性夹层间距为H。
(32)
(33)
式中:VCyl为图6中灰色圆柱体的体积;SCyl为该圆柱体侧面(即与空气接触表面)的面积。

图6 四周开放的建筑层间爆炸示意图Fig.6 Sketch map for the explosion of the open-sided multi-storey buildings
3 算例和验证分析
3.1 与解析公式对比验证
文献[37]中给出的位于钢板、混凝土、岩石等刚性地面的爆炸冲击波超压峰值计算公式为
(34)
式(34)中:1.259 m/kg1/3≤Z≤18.899 m/kg1/3。
由式(24)可知,此时VECF=2,将其代入式(23),再用式(23)计算得到的等效比例距离Z*代替文献[37]中给出的自由场空气中爆炸冲击波超压峰值计算公式,即式(5)中的Z,可得
(35)
式(35)中:1.259 9 m/kg1/3≤Z≤18.898 8 m/kg1/3。比较式(34)、式(35),发现它们是高度一致的,只是在小数位数上存在细微的差别,这表明使用体能量密度因子方法推导得到的刚性地面爆炸冲击波超压峰值计算公式是合理的。
文献[35,37]指出在计算地面接触爆炸的冲击波超压峰值时,采用自由场空气中爆炸冲击波超压峰值公式,将式中当量乘以2即可。这种处理本质上是利用了“能量密度”概念,引入体能量密度因子方法给出了比较规范的物理和数学推导与证明。
3.2 与实验结果对比验证
文献[26]中给出了250 kg TNT装药在截面面积为 10 m2的坑道内爆炸时不同位置处的冲击波超压峰值实验测试结果和数值计算结果,如表1所示。
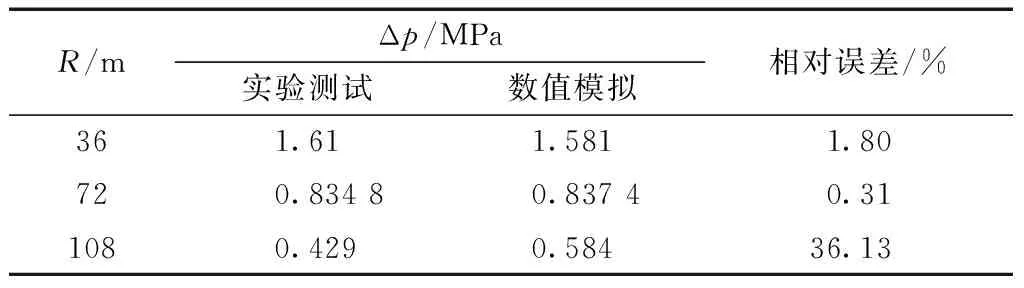
表1 不同位置处冲击波超压峰值实验结果[26]Table 1 Experimental results of shock wave overpressure peak at different positions[26]
文献[26]利用三维数值模拟计算程序对实验情况进行了大量的数值计算,从而拟合出计算该坑道内冲击波超压峰值的经验公式为

(36)
式(36)中:Δp为超压峰值,MPa;W′为TNT爆炸当量,kg;A为坑道截面面积,m2;R为爆心距离,m。
利用体能量密度方法对文献[26]中的情况进行计算,并与实验结果进行比较分析。
(37)
用式(37)中的Z*代替式(5)中的Z,即得文献[37]中给出的坑道内爆炸解析计算公式。上述推导过程也证明了文献[37]本质上是利用了面体能量密度因子的概念计算坑道内爆炸冲击波超压峰值。
根据上述方法,得到不同计算公式下超压峰值随爆心距离变化曲线(图7),可以看出,基于体能量密度因子得到的计算结果与实验结果吻合得很好,而基于面能量密度因子得到的计算结果与实验结果误差比较大。以文献[36-37]中的自由场超压峰值计算公式为基准的计算结果与实验和数值模拟结果高度吻合。表2给出了3个位置处数值计算结果、基于式(5)的体能能量密度因子法和面能量密度因子法计算结果与实验测量数据的比较,同样证明了上述结论。

表2 不同位置处冲击波超压峰值结果对比Table 2 Comparison of peak values of shock wave overpressures at different locations

图7 不同方法得到的坑道内冲击波超压峰值结果比较Fig.7 Comparison of peak values of shock wave overpressure in tunnel computed by different methods
因此,对于两端开放无限长坑道内的爆炸,采用体能量密度因子方法计算超压峰值是可行的。
4 结论
基于量纲分析和Taylor展开推导了自由场空气中爆炸冲击波超压峰值多项式形式的解析计算公式,引入体能量密度因子方法将上述公式推广到复杂几何布局情形,为快速计算复杂几何布局条件下爆炸冲击波超压峰值提供了有效的方法。通过与地爆解析公式、实验数据和数值模拟结果比较,对本文方法进行了验证,得出以下结论。
(1)目前工程上普遍使用的自由场空气中爆炸冲击波超压峰值经验公式,可以通过量纲分析和Taylor展开从物理和数学上比较严格的推导出其统一的形式,如式(16)所示。
(2)基于上述推导过程,深刻理解式(16)所代表的物理本质,进而引入体能量密度因子的概念,将自由场空气中爆炸冲击波超压峰值解析计算公式推广到复杂几何布局的情形,如式(22)、式(23)所示。
(3)工程上普遍使用的地爆冲击波超压峰值解析计算公式可以通过提出的体能量密度因子方法推导得到,即目前已有的地爆超压峰值解析计算公式可以看作是由体能量密度因子方法得到的一个特例。
(4)使用本文方法解析计算的结果与坑道内爆炸实验数据符合得较好,这表明本文方法可以应用于工程领域复杂几何布局条件下爆炸冲击波超压峰值的快速估算。
