基于图像处理的档案盒标签的检测技术研究
2021-10-20徐寅林
李 婧,苏 叶,徐寅林
(南京师范大学计算机与电子信息学院,江苏 南京 210023)
目前国内外常见的档案检测识别方法是基于条形码、QR码或RFID技术,通过扫码或读取档案盒电子标签进行识别. 基于条形码或QR码技术需用机械手夹持条码枪移动读取,实时性差. RFID技术是将射频读卡器排列成行,与档案盒标签一一对应,该方法成本高且易受干扰. 由于档案盒的检测识别与图书的检测识别具有一定的相似性,因此可借鉴图书的检测识别技术来研究档案盒检测识别的相关技术.
近年来,由于人工智能技术的快速发展,出现了通过拍摄图书书脊进行检测识别的技术. 该方法利用摄像头或其他成像设备采集到书架上的书脊图像,通过识别书脊上的文字信息(如书名、作者、出版社等)来识别图书[1-2],准确率高、实时性好且方便快捷. 由于不同图书的书脊大小、书名及颜色等特征差异较大,书脊检测识别可有一定的容错度而不影响图书的区分. 本文研究的档案盒标签往往差异不大,如人事档案标签一般单位、部门、籍贯等都一样,只在具体姓名或编号部分略有不同,因此仅通过文字识别技术很难达到较高的检测准确率. 本文提出一种基于图像处理的档案盒标签检测方案,利用摄像头实时采集回转库档案柜窗口区域的整排档案盒的标签图像,通过深度学习U-Net[3]网络将整排档案盒标签图像进行分割,对一些形变的图像进行仿射变换矫正,裁剪得到独立的标签图片,最后使用surf[4]匹配算法对标签图像进行检测. 实验结果表明,本文提出的算法具有较高的匹配正确率.
1 图像预处理
1.1 标签图像分割
将摄像头固定在距离档案柜窗口区前方约50 cm处,利用摄像头视角范围大、拍摄清晰且不易变形的特点,只需要设置两个摄像头即可以获取回转库档案柜窗口区全部档案盒的标签图像. 摄像头得到的是窗口区的全部档案盒图片,首先需要分割得到独立的一本本档案盒图片才能进行后续的检测识别. 由于传统的分割方法易受噪声等干扰[5],本文采用深度学习的U-Net网络进行分割. U-Net模型是一个语义分割模型,可实现端到端的分割. 具体方法是利用卷积进行下采样,提取出一层又一层的特征,利用这些特征再进行上采样,最终得到类别数量的特征图[6]. U-Net网络通过上采样过程中的级联,使得浅层特征和深层特征结合起来,在图像分割效果上有着不错的表现.
首先对U-Net网络进行训练,以计算出最佳网络参数. U-Net分割模型的训练需要原图和与其对应的标签图片两个文件,其中标签图片通过labelme软件对原图进行手动标注可得. 图1所示为具体的训练与测试过程. 本文的训练集包含107张样本图片,测试集包含37张图片. 训练过程中损失函数loss在迭代20次后趋于稳定.

图1 分割流程图Fig.1 Segmentation flow chart
1.2 标签图像的“平直性”纠正
由于摄像头固定在桌面上,必须以一定的仰角才能对准窗口区档案盒背脊,因而拍摄出来的档案盒图片会有一定的角度倾斜,进行矩形裁剪可能会得到残缺或冗余的档案盒图片. 为了提高后续检测的正确率,需对图片进行矫正. 摄像头仰角拍摄造成的图片畸变以剪切形变为主,本文采用仿射变换对其进行角度调整.
对分割预测图片进行轮廓检测得到每本档案盒轮廓的点的合集,通过最小外接矩形方法即可得到每本档案盒的倾斜角度θ,角度范围为-90°~0°. 实际计算时,若倾斜角度小于-45°,则在原来角度上增加90°;若倾斜角度大于-45°,则直接对角度反转,最终实现图片的旋转. 最后,对每本档案盒旋转后的图片进行裁剪,即得到单独的档案盒图片.
2 图像配准
由于档案盒图片大多背景相同,只有少数细节存在差异,因此图书识别中常用的文字识别技术并不适用于档案盒标签的检测识别. 考虑到档案盒的局部差异性,本文采用surf匹配算法,主要包括特征点提取、特征点描述和特征点匹配. 首先构建Hessian矩阵产生兴趣点,然后构建尺度空间,对特征点进行非极大值抑制得到最终稳定的特征点,再利用特征点的Harr小波特征确定特征点主方向,生成特征描述子,最后计算出特征点之间的欧氏距离以确定匹配好坏[7].
2.1 图像特征提取
surf算法的关键是利用Hessian矩阵来得到稳定的特征点,为特征点提取做准备. Hessian矩阵为:
(1)
surf算法使用盒式滤波器,从而用积分图像加速卷积. 图2从左到右分别为y方向和xy方向的高斯二阶偏导数模板及其近似表示,记为Dyy、Dxy,此时Hessian矩阵的判别式为:
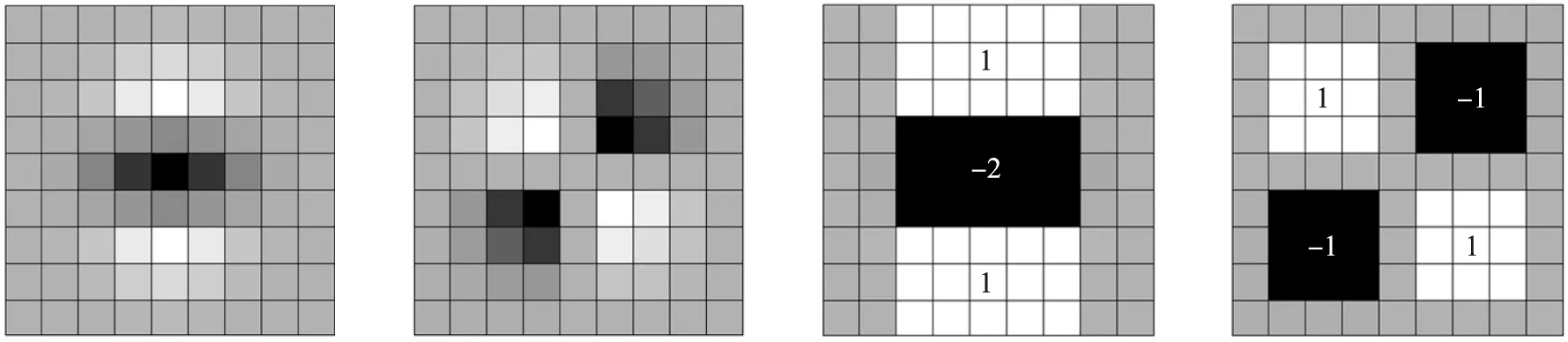
图2 高斯二阶偏导数的近似表示Fig.2 Approximate representation of Gaussian second-order partial derivative
det(H)=DxxDyy-(ωDxy)2,
(2)
式中,Dxx为x方向的高斯二阶偏导数近似表示;ω一般取0.9,可修正盒式滤波器的近似误差.
surf算法在不改变目标图像大小的情况下,逐渐增大盒式滤波器的模板尺寸,从而获得图像金字塔,该方法提高了运算效率.
通过Hessian矩阵判别式的值得到极值点后,对极值点进行非极大值抑制,将极值点与其图像域和尺度域的所有相邻点进行比较,当其大于所有相邻点时,确定该点为特征点[8-9].
2.2 特征点描述
首先,为了确保特征点的旋转不变性,需给每个特征点分配一个主方向. 在以特征点为中心的领域内,计算60°范围内所有点的Harr小波特征总和,再依次旋转0.2个弧度重复计算[10],最终特征点的主方向为矢量值最大的方向.
提取特征点周围4×4个矩形区域块(每个区域边长为5s×5s,s为盒式滤波器的边长尺寸),方向沿着特征点主方向,使用尺寸为2s×2s模板的Harr小波计算每个区域块内25个像素点的Harr小波特征之和以及Harr小波特征绝对值之和,最终surf特征描述子共有4×4×4=64维[11].
2.3 特征点匹配
surf算法中常用欧式距离衡量特征点是否匹配,本文采用Flann(快速最近邻搜索)匹配算法[12-13]. 在Flann算法中,第一个匹配的是最近邻,第二个匹配的是次近邻,可通过查看两个特征点之间距离的不同来判断是否匹配成功. 本文经实验对比,得到设定最近邻与次近邻距离比值小于0.7为最佳匹配;当设定阈值小于0.7时,随着阈值减少,匹配错误数增多;当设定阈值大于0.7时,随着阈值增大,误匹配数增多.
3 实验分析
论文设计了不同标签的107个档案盒作为实验数据集. 首先,每本档案都要录入一个图片作为比对的对象,即底库照片,共有107张作为实验比对的底库标准集. 然后将每本档案盒摆放在架子的不同位置拍摄,共采集到1 498张图片. 数据集的制作方法有两种,第一种将实际拍摄的图片,按U-Net生成的预测图片模板大小进行调整,然后分割、仿射变换后作为测试集1. 该方法预处理裁剪出来的单本档案盒图片宽度小,拍摄照片调整尺寸为正方形后造成图片质量下降,档案盒图片文字也不清晰,影响算法的正确率. 第二种方法是将U-Net得到的掩模图片调回到原图尺寸,对原图进行掩模、分割、仿射变换、裁剪等一些列操作,可以得到高质量的测试集2. 表1为两种测试集在surf算法下的正确率,可以看出测试集图片的质量对算法有较大影响.

表1 不同测试集的匹配正确率Table 1 Matching accuracy of different test sets
3.1 Hessian阈值对surf算法的影响
由于在surf算法中Hessian阈值的设定对匹配结果的好坏有一定影响,阈值越高,检测到的特征点越少,特征点越稳定. 因此,可用试探法来得到该档案盒匹配的最优检测. 图3所示为不同Hessian阈值下对应的匹配错误数目,可以看出,在阈值590-610之间,匹配的错误数最少,趋于稳定不再减少;而当阈值过高时,则可能因为检测到的特征点太少而无法匹配. 因此,本文取阈值600为最佳值,匹配正确数目为 1 492,正确率达到99.60%.

图3 不同阈值下匹配错误数Fig.3 Number of matching errors underdifferent thresholds
3.2 surf算法的鲁棒性研究
3.2.1 光照强度对图片匹配正确率的影响
实际应用场景下,可能存在各种各样的环境光强,光照不变性是surf算法的一个优点. 图4所示为不同光照强度下的匹配正确数,其中光照强度等于1.0为原图. 从图4可以看出,当光照强度为0.4~1.6,匹配正确数变化不大,匹配结果较好;当图片过亮或过暗时,surf算法性能逐渐下降,这充分反应了surf特征点检测具有很强的光照不变鲁棒性.

图4 不同光照强度下匹配正确数Fig.4 Matching correct number underdifferent light intensity
3.2.2 噪声对图片匹配正确率的影响
实际场景中采集得到的档案盒图片还可能存在许多干扰,最典型的有角落位置档案盒光照明暗不均、档案盒存放时间过久纸张泛黄或者沾染上灰尘等. 为考察这些噪声对图片匹配正确率的影响,本文模拟测试了各种噪声情况下surf算法的稳定性,其匹配结果如表2所示. 其中明暗不均与泛黄图片受干扰影响较少,稳定的特征点较多,正确率较为稳定;灰尘图片受到较多噪声点干扰,匹配效果较差.

表2 不同干扰下的匹配正确率Table 2 Matching accuracy under different interference
分析surf的工作原理可以发现,特征点的提取主要依赖于Hessian矩阵判别式,判别式为局部极大值时,该点是领域内最亮或最暗的点,从而确定特征点位置. 而矩阵判别式的值与高斯二阶偏导数及图像的卷积值有关. 局部图像灰度的缓慢变化对卷积值影响较小,因此surf算法对图片偏亮、偏暗、缓慢变化的明暗不匀及泛黄具有很好的抗干扰能力. 对于灰尘干扰,其颗粒大小往往和图像斑点尺度相近,这严重影响了surf的特征点提取,从而影响了图片的匹配正确率.
对于实际场景下受到不同污染的档案盒图片,可以对其进行处理,以提高匹配的正确率. 对明暗不均和泛黄的档案盒图片,尽管surf算法抗干扰能力很强,但通过对图片进行适当处理,可以使匹配效果更好. 本文考虑直方图均衡算法和自动色彩均衡(ACE)算法进行处理. 由于直方图均衡化算法一般用于灰度图像,对于档案盒图片这种彩色图像易出现颜色不均、失真等问题. 对明暗不均的加噪测试集进行直方图均衡化,实验测得的匹配正确率约为95.13%,反而降低了正确率. 自动色彩均衡(ACE)算法能够考虑到图像中亮度和颜色的空间位置关系,实现具有局部和非线性特征的图像亮度、色彩及对比度调整,可有效提高匹配正确率.
对有灰尘的档案盒图片,本文考虑了中值滤波、非局部平均去噪等方法. 中值滤波是指在以某点像素为中心的邻域内,对所有像素进行排序,将排序中的中值作为该点的响应. 该算法对于去除椒盐噪声效果显著. 对灰尘图片进行中值滤波,可明显去除大部分噪声,此时测得的正确率约为93.79%. 对于剩余的干扰可再采取非局部平均去噪的算法进行处理,该算法是通过对整幅图像中相似区域求平均进行去噪,需注意亮度权重衰减参数h的选择,该值设置高虽可更好地消除噪声点,但同时也会消除图片的细节.
图5显示了不同亮度权重衰减参数测得的匹配错误数,可以看出,当参数设为10.2时,匹配正确率最优. 由于灰尘档案盒图片本身对比度不高,经中值滤波后直接进行非局部平均去噪处理会丢失很多细节信息,因此可以对灰尘档案盒图片先进行自动色彩均衡,增强对比度后再进行非局部平均去噪处理,以提升匹配效果. 经处理后的档案盒匹配正确率如表3所示.
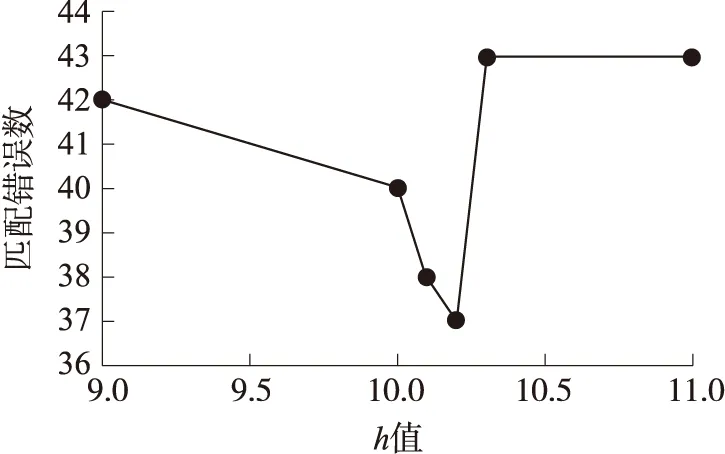
图5 不同h值下匹配情况Fig.5 Matching under different h values

表3 处理后的匹配正确率Table 3 Matching accuracy after processing
经去噪处理后的图片检测到的特征点数增多,匹配点对数增多,误匹配对数减少,匹配效果较未处理之前有显著提升. 可见,surf算法对于一定程度下光照变化及实际情况下明暗不均、泛黄干扰均能保持着较好的匹配效果,鲁棒性较好.
4 结论
本文阐述了基于图像的档案盒标签检测技术,通过使用U-Net网络进行档案盒图片分割、对形变档案盒进行仿射变换等一系列预处理得到独立档案盒图片,使用surf算法进行档案盒图片的匹配,并测试了在不同光照强度及不同噪声干扰下surf算法的匹配性能,最后讨论了在噪声干扰下的应对方法. 由实验结果可知,该技术对回转库档案盒的检测有较好的效果.
