基于子带谱熵法和PSO-GA-SVM的汽车鸣笛识别
2021-10-20余凌浩陆铁文曾毓敏
余凌浩,陆铁文,李 晨,曾毓敏,袁 芳
(1.南京师范大学计算机与电子信息学院/人工智能学院,江苏 南京 210023)(2.杭州爱华智能科技有限公司,浙江 杭州 311121)
近年来,交通噪声的关注度日益提升. 鸣笛噪声是交通噪声的主要组成成分,汽车在禁鸣区违章鸣笛,会严重影响他人的生活、学习与工作. 为了遏制违章鸣笛,鸣笛抓拍系统应运而生. 鸣笛抓拍系统会实时检测当前的声压级,当声压级超过一定阈值时,系统通过远场波束形成技术定位声源的位置并进行音视频记录[1]. 然而交通环境中声源情况非常复杂,有很多非鸣笛声也能触发鸣笛抓拍系统的阈值,只依靠声压级触发门限会出现较多误判的情况. 这也是目前鸣笛抓拍系统应用较少的主要原因. 因此,对鸣笛抓拍系统采集的样本进行鸣笛与非鸣笛的分类是非常有必要的.
在汽车鸣笛识别方面,目前已有许多学者进行了研究[2-8],较为常用的方法主要分为以下两类:(1)阈值判断,如文献[8]中使用的短时能量和短时过零率法等. 该方法将特征值高于或低于一定门限的声音样本直接进行分类,其分类效果主要取决于特征和阈值的选取. (2)机器学习,如文献[2]中使用的卷积神经网络、文献[6]中使用的隐马尔科夫模型等. 该方法首先对样本提取特征,通过训练一定数量的样本得到一个模型,再通过采集的样本是否与模型相匹配来进行分类.
进行阈值判断时,阈值的设置会直接影响分类结果的准确性,然而交通环境中声源情况非常复杂,会给阈值设置带来较大阻碍. 机器学习虽然准确率较高,但对模型有比较高的要求. 如果实测的鸣笛样本中含有较多噪声,也会对分类准确率产生很大影响. 因此,我们需要结合实际交通环境中的鸣笛噪声,研究具有较高准确率的鸣笛识别算法.
由于鸣笛声具有丰富的谐波特征,其子带谱熵值相对较低. 相比较于传统的短时能量和短时过零率特征,子带谱熵具有更高的区分度[9-10],阈值的设置具有普适性. 机器学习主要分为传统机器学习和深度学习两大类. 深度学习非常适合处理大数据下的特征,但是在较小的数据量下,深度学习并没有表现出很好的效果,并且由于其计算量过大,很难满足实时性的需求. 而支持向量机(support vector machine,SVM)作为传统机器学习的方法,在进行小样本集分类时效果较好[11].
SVM参数优化的传统方法是网格搜索法,该方法通过遍历参数的所有组合来选取最优结果,运行速度较慢. 我们使用粒子群优化(particle swarm optimization,PSO)和遗传算法(genetic algorithm,GA)的融合(PSO-GA)来优化SVM的参数[12-13],在准确率没有降低的情况下,提高了选取最优参数的速度.
本文结合了阈值判断和机器学习的方法,提出了一种基于子带谱熵法和PSO-GA-SVM的汽车鸣笛识别算法. 仿真结果表明,该算法具有较好的鲁棒性. 在对实际采集样本的鸣笛识别中,本文算法也取得了较高的准确率.
1 算法介绍
1.1 算法总流程
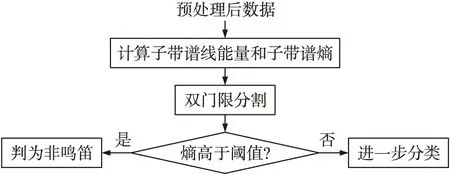
本文首先使用子带谱熵法对鸣笛抓拍系统采集的声音样本进行初判,将子带谱熵高于阈值的样本直接判定为非鸣笛样本. 为了使SVM训练出较好的模型,在子带谱熵法中再结合子带谱线能量门限,对初判为鸣笛的样本中的疑似鸣笛部分进行分割. 然后使用SVM对分割结果进行进一步分类,并使用PSO-GA来优化SVM的参数. 算法总流程如图1所示.

图1 算法总流程Fig.1 Overall algorithm process
1.2 预处理
文中预处理的主要流程为:带通滤波、预加重、分帧、加窗.
一般汽车鸣笛的频率分布在1 500~6 000 Hz. 为了保留汽车鸣笛的主要特征并去除噪声的干扰,对声音样本进行1 500~6 000 Hz的带通滤波.
预加重是一个一阶高通滤波器,用一阶FIR滤波器表示为:
s′(n)=s(n)-as(n-1).
(1)
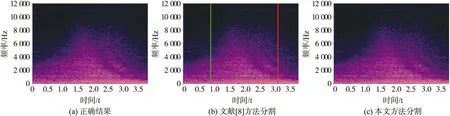
式中,a为一常数,s(n)为原始信号,s′(n)为预加重后的信号. 预加重可以对信号进行高频提升,使频谱变得更平坦,减少频谱的动态范围. 一般来说,0.9 分帧可以将一段较长声音信号分成多个小段,使每小段声音信号可以作为平稳信号来处理. 为了使每一帧信号之间平滑地过渡,两个相邻帧之间需要有一些重叠区域. 本文中帧长选为50 ms,帧移长度选为帧长的1/3. 加窗可以避免因信号两端不连续而导致的频谱泄漏. 本文选用汉明窗作为窗函数w(n),若共有N个采样点,则第n个采样点的窗函数公式为: (2) 1.3.1 算法介绍 子带谱熵的思想是将每一帧的频谱分成若干个子带,这样就消除了每一条谱线受噪声影响的问题. 设每个子带由4条谱线组成,共有Nb个子带. 第i帧中的第n个子带的谱线能量E(n,i)为: (3) 式中,Yi(k)为傅里叶变换后的谱线能量. 子带谱线能量的概率分布p(n,i)为: (4) 引入一个正常量C,得到新的子带谱线能量的概率分布式: (5) 文献[9]中推导证明,在噪声环境下,引入正常量C后,分割的准确度能得到提高. 本文中C取0.1. 子带谱熵Hb(i)为: (6) 1.3.2 算法流程 子带谱熵法的主要流程如图2所示. 在信号的子带谱线能量包络线上选取一个较高的阈值eth2,包络线与eth2相交于左右两个点A和B. 认定高于eth2的部分一定是鸣笛,而鸣笛的起止点应该在AB段之外. 再在信号的子带谱线能量包络线上选取一个较低的阈值eth1,从A点向左、从B点向右搜索,分别找到包络线与eth1相交的左右两个点C和D,如图3(a)所示.CD段即为基于子带谱线能量门限分割的鸣笛部分. 图2 子带谱熵法流程Fig.2 Sub-band spectral entropy method process 图3 双门限分割示意图Fig.3 Schematic diagram of double threshold segmentation 在对应的子带谱熵包络线上,从C点向右、从D点向左进行更加细致的分割,找到子带谱熵低于阈值eth3的左右两个点E和F,如图3(b)所示.EF段即为基于子带谱线能量和子带谱熵双门限分割的鸣笛部分. 图3(c)为声音样本的频谱图以及分割结果,左边的竖线为分割的起始点,右边的竖线为分割的停止点. 由于汽车鸣笛声具有丰富的谐波特征,其子带谱熵值相对较低,子带谱熵特征的区分度更高. 为了验证子带谱熵法的有效性,我们使用文献[8]的短时能量和短时过零率法与本文的子带谱熵法进行了对比实验. 实验结果如图4和图5所示. 图4的样本中没有鸣笛声,正确的结果应没有分割线,如图4(a)所示. 文献[8]的方法产生了分割线,而本文的方法没有产生分割线,并将其分类为非鸣笛样本. 图5的样本中含有鸣笛和噪声,正确的分割结果如图5(a)所示. 文献[8]的方法不仅分割出了鸣笛部分,还分割出了多个噪声片段. 而本文的方法则准确地分割出了鸣笛声,没有分割出噪声部分. 图4 对一段非鸣笛声音样本的分割Fig.4 Segmentation of a non-whistle sound samples 图5 对一段含有鸣笛和噪声的声音样本的分割Fig.5 Segmentation of a sound samples with car whistle and noise 使用子带谱熵法可以将子带谱熵高于阈值的样本直接判为非鸣笛样本,如图4(c)所示. 然而在实际交通环境中也存在一些非鸣笛声(如汽车转向提示声、公交车报站声、警笛声等),由于具有一定的谐波特征,产生了分割结果,会被子带谱熵法误判为鸣笛声,如图6所示. 因此,我们需要对子带谱熵法的分割结果进行进一步的分类,来消除此类误判. 图6 对部分非鸣笛样本的分割Fig.6 Segmentation of some non-whistle sound samples 1.4.1 算法介绍 SVM是一种二分类模型. 设样本集为(xi,yi),其中xi为样本特征,yi为类别符号. SVM的目标是寻找一个分类面ωTx+b=0将样本正确地分成两类,且使‖ω2‖最小. 在样本集线性不可分时,需要引入惩罚因子c和核函数K(xi,xj)来进行分析. 核函数可以将低维向量内积的结果转化为高维向量内积的结果,但不需要在高维中进行计算. 本文选用的核函数为径向基核函数, K(xi,xj)=e-g‖xi-xj‖2. (7) 惩罚因子c和核函数参数g对SVM的分类性能有很大的影响. 本文使用PSO-GA来优化c和g参数. PSO将粒子i在搜索空间中的飞行速度表示为向量vi,位置表示为向量xi. 在每一次迭代中,计算每个粒子的适应度,通过个体极值pbest和全局极值gbest来更新每一个粒子的速度和位置,如下两式所示: vi=K[vi+φ1r(pbest-xi)+φ2r(gbest-xi)], (8) xi=xi+vi. (9) 式(8)中,r为均匀分布在(0,1)之间的随机数,K由下式表示[14]: (10) 本文中φ取4.1,则K取0.730. GA将搜索空间中每一个可能的解编码为染色体,随机选择一组染色体来形成初始群体. 在每一次迭代中,计算每个粒子的适应度,按照适应度大小的顺序来选择个体,进行交叉、变异等操作. 反复执行遗传操作,直到满足终止条件为止. 1.4.2 算法流程 PSO-GA-SVM主要流程如图7所示,其主要步骤如下: 图7 PSO-GA-SVM流程Fig.7 PSO-GA-SVM process 步骤1 对训练集进行k折交叉验证. 本文中k取5. 步骤2 将搜索空间中每一个c和g可能的解编码为染色体,随机选择N个染色体来形成初始种群,并初始化粒子速度. 计算每一个粒子的适应度,求出pbest和gbest. 本文中N取20. 步骤3 按照式(8)和(9)更新每一个粒子的速度和位置. 步骤4 按照适应度选出N-1个粒子,对它们进行交叉、变异操作,再与上一代的最优粒子组合成新的N个粒子. 计算每一个粒子的适应度,更新pbest和gbest. 步骤5 转步骤3,直到满足一定迭代次数为止. 本文中迭代次数取100. 步骤6 输出最优c和g. 步骤7 将最优c和g代入SVM的c和g参数中,对测试集进行分类. 本文使用CPU为Intel i7-8750H、内存为8G的计算机作为硬件平台. 本文中所有音频的格式为wav格式,位深度为32位. 所有程序均在Python 3.7.0下编写. 每次实验从数据集中随机选取80%的样本作为训练集,剩下20%的样本作为测试集,计算100次实验的平均准确率. 本文选用Mel频率倒谱系数作为分类器输入的声音特征[15],其中Mel滤波器的个数选为96个,离散余弦变换后取第2~65维,再对每一帧信号求平均,最终形成一个64维的向量. 本节中对不同底噪、不同信噪比的声音样本进行仿真实验. 鸣笛声取自杭州爱华智能科技有限公司提供的纯净鸣笛声样本,包含奥迪A3、大众高尔夫、吉利等13种不同车型的鸣笛声,共120个. 非鸣笛声取自UrbanSound8K数据集中的城市声音样本,包含空调外机声、小孩玩耍声、警笛声等8种类型的声音,共211个. 本节中音频的时长为1 s,采样频率为48 kHz. 为了模拟鸣笛抓拍系统的采集方式,每个声音样本中只有0.25 s存在待识别的声音,并且随机设置该声音在音频中的起始位置. 为了验证本文算法的鲁棒性,在上述声音样本的基础上,分别添加信噪比为20 dB、10 dB、5 dB、0 dB的白噪声和粉噪声作为底噪进行仿真实验. 白噪声和粉噪声取自NOISE92数据集. 仿真实验结果如表1所示. 分析表1可知,在信噪比较高的情况下,本文算法对仿真样本的识别准确率可以达到99%以上. 随着信噪比不断降低,本文算法的识别效果虽然也有所下降,但依然维持在相对较高的准确率上. 在极差的信噪比环境下(信噪比为0 dB时),本文算法依然能够有75%以上的准确率. 说明本文算法具有较好的鲁棒性. 本节中对杭州爱华智能科技有限公司的鸣笛抓拍系统实际采集的1 067个声音样本进行鸣笛识别,其中包括683个不含有鸣笛声的样本,包含卡车发动机声、汽车转向提示声、公交车报站声、警笛声等超过10种城市环境音. 包括384个含有鸣笛声的样本,包含各种车型的鸣笛声,背景噪声中也存在多种上述城市环境音. 本节中音频的时长为3.8 s,采样频率为24 kHz. 我们选择文献[2]算法、文献[7]算法与本文算法进行了对比实验. 实验结果如表2所示. 从表2可见出,本文算法相比文献[2]算法准确率提高了21.3%,相比文献[7]算法准确率提高了14.4%. 文献[2]和文献[7]只使用深度学习的方法对声音样本进行分类,而本文首先使用子带谱熵法对声音样本进行初判和分割,再使用分类器对分割结果进行进一步分类. 同时,文献[2]和文献[7]中深度学习的方法在样本数量较少时分类效果并不理想,而本文使用的PSO-GA-SVM更加适合小样本集的分类. 因此,本文算法在汽车鸣笛识别上具有更高的准确率. 表2 不同算法的平均准确率Table 2 Average accuracy with different method 我们使用子带谱熵法结合文献[7]使用的反向传播神经网络(backpropagation neural network,BPNN)和本文使用的PSO-GA-SVM进一步进行了对比试验. 实验结果如表3所示. 表3 使用子带谱熵法前后的平均准确率Table 3 Average accuracy with and without sub-bandspectral entropy method 子带谱熵法对非鸣笛样本的误判率在1%以内,但是对鸣笛样本的误判率在34%以上,不能满足鸣笛抓拍系统对准确率的要求,因此需要对子带谱熵法初判为鸣笛的样本作进一步的分类. 由表3可知,使用子带谱熵法前,BPNN和PSO-GA-SVM的准确率并不是非常理想,而使用子带谱熵法后,两种分类器的准确率均有了较大提高. 这是因为子带谱熵法可以分割出疑似鸣笛的部分,大幅减少了噪声对分类器模型造成的影响. 同时从表3中还可以看出,本文使用的PSO-GA-SVM相比较于BPNN具有更高的准确率,更加适合小样本集的分类. 此外,由于本文使用的声音特征维数较低,仅有64维,提取特征以及分类的速度较快,在本文使用的计算机上处理一个样本仅需约0.3 s,可以很好地应用到实时检测中. 针对现有的汽车鸣笛识别算法易受噪声影响、计算量较大的问题,本文提出如下算法:首先利用阈值判断对声音样本进行初判,使用子带谱熵法分割出样本中疑似的鸣笛部分;然后利用机器学习对疑似鸣笛样本作进一步分类,使用PSO-GA-SVM训练模型,最终分类出所有的鸣笛与非鸣笛样本. 实验表明,本文算法准确率较高且计算量较小,可以满足鸣笛抓拍系统实时检测的要求.1.3 子带谱熵法



1.4 PSO-GA-SVM

2 实验及结果分析
2.1 仿真实验
2.2 结果分析


3 结论
