空间平滑MUSIC算法的相干信源DOA
2021-10-20杨志强
郑 超 杨志强
(四川九洲空管科技有限责任公司 四川绵阳 621000)
0 引言
空间谱估计是阵列信号处理中的重要领域,想要得到信号的波达方向(DOA),就要得到信号的空间谱。由于实际空间环境中多径传播等因素的影响,存在大量的相干信号源。当信号源完全相干时,阵列接收数据的协方差矩阵的秩降为1[11],就会导致信号子空间维度数小于信号源数目,对于一般的DOA估计算法,如MUSIC算法,由于信号源子空间与噪声子空间相互渗透影响,所以不能对相干信号源进行有效的分辨测向[1],利用平滑MUSIC算法可以解决传统MUSIC算法不能估计相干信号源的问题。
1 MUSIC算法原理以及仿真分析
1.1 MUSIC算法原理
若接收信号为窄带,以线阵为例,信源和天线阵列是在同一平面,入射到天线阵信号的数目为K,以来波方向θK(k=1,2,…,K)入射M根天线,阵元间距为d,如图1所示[2]。
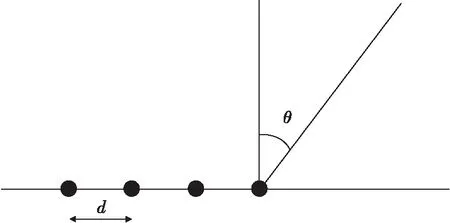
图1 均匀线阵
假设入射到天线阵列的信号向量为s(n)为
s(n)=(s1(n),s2(n),…sK(n))
(1)
均匀线阵的阵列相应矢量为
(2)
方向矩阵为
A=[a(θ1),a(θ2),…,a(θK)]
(3)
阵列接收到信号为入射到天线阵列单元信号的总和,所以有[3]
x(n)=a(θ1)s1(n)+…a(θK)sK(n)
(4)
在现实环境下存在加性噪声,因此阵列接收信号表示为
x(n)=As(n)+v(n)
(5)
式(5)中,x(n)为阵列的接收数据向量,A是阵列的方向矩阵,s(n)为空间信号向量,v(n)是白噪声向量。接收信号向量的空间相关矩阵可表示为[4]
R=E[x(n)xH(n)]=ARsAH+σ2I
(6)
对R进行特征值分解,设λ1,λ2,…,λM为特征值,u1,u2,…,uM是对应的特征向量。特征值中与信号有关的λ1,λ2,…,λK,其余M-K特征值是与噪声有关的,由此定义噪声子空间的概念[5]
G=[uK+1,uK+2,…,uM]
(7)
MUSIC的谱估计可以表示为[6]
(8)
MUSIC谱函数中的K个峰值位置,就是信号入射的天线阵方向θK。
1.2 MUSIC算法仿真分析
首先用Matlab构建三路非相干信源,仿真采用8天线阵子,进一步仿真MUSIC算法,仿真参数如表1所示。

表1 实验条件
在表1的条件下,用Matlab仿真给出了MUSIC测向结果,结果如图2所示。
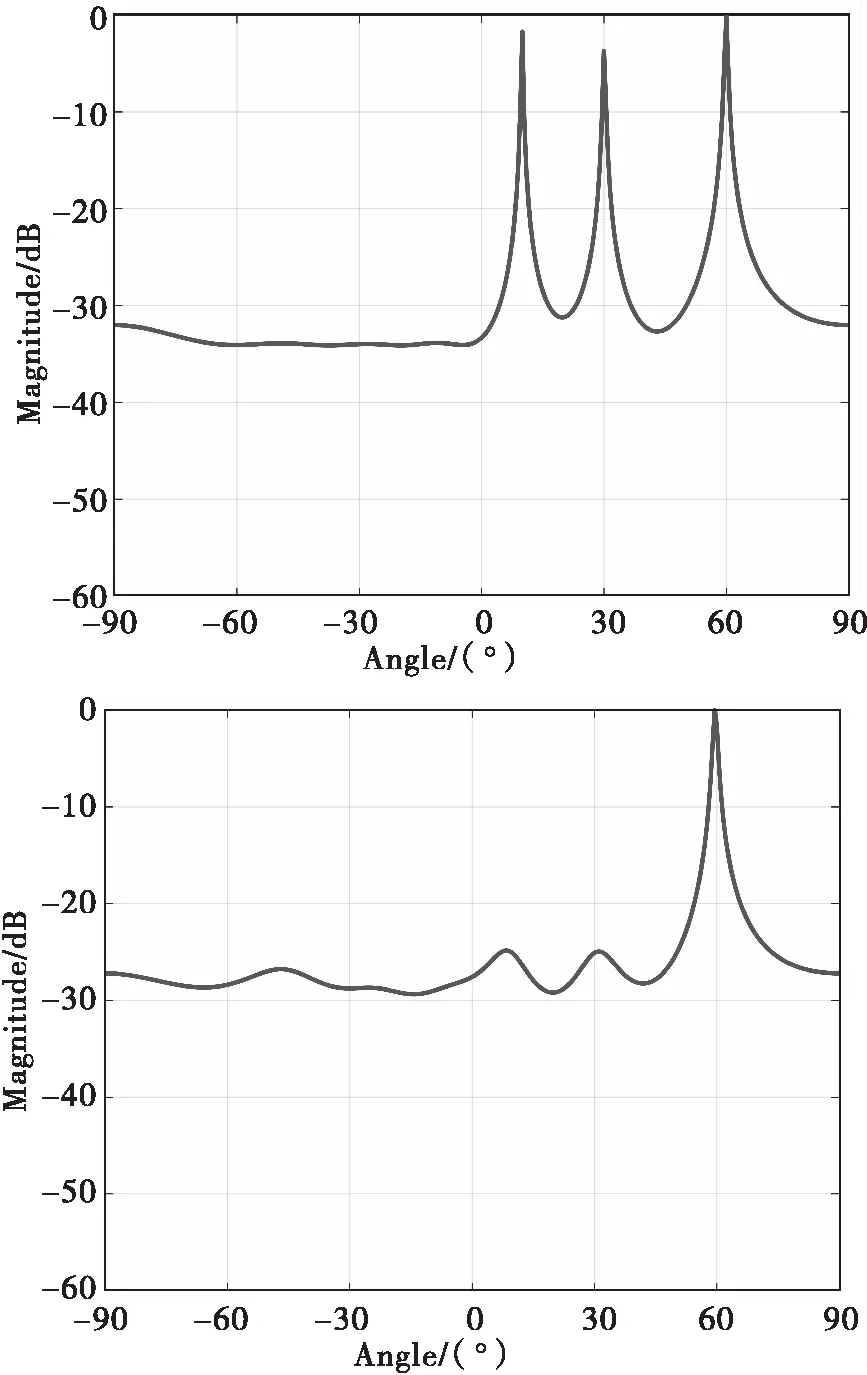
图2 MUSIC算法仿真
图2中,上图信源为3路非相干信源,下图信源中方向10°和方向30°为相干的信源。根据图2的仿真结果可知,MUSIC算法可以有效地分辨测向非相干信源,但是不能有对相干信源进行有效地分辨测向。
2 平滑MUSIC算法原理及仿真分析
目前相干信号源的处理算法可以分为两类:第一类是降维处理算法,第二类是非降维处理算法。其中,空间平滑算法、矢量奇异值类算法、矩阵分解类算法为第一类方法;Topelitz类算法、改进MUSIC算法和基于特征空间的DOA估计算法为第二类处理方法[7-8]。
(x)通过加权集结算子将子组Ey(y=1,2,…,10)群决策矩阵y=1,2,…,10)转化为组E群决策矩阵D=(dij)m×n(i1,2,...,10,j=1,2,3,4,y=1,2,…,10)。
2.1 空间平滑MUSIC算法原理
空间平滑MUSIC算法专门为解决相干而提出的一种超分辨算法,该算法只适合于均匀线阵。空间平滑算法利用子阵平滑恢复数据协方差矩阵[9],主要有:
1)前向平滑MUSIC算法(FSS);
2)后向平滑MUSIC算法(BSS);
3) 双向平滑MUSIC算法,即修正的空间平滑MUSIC算法(MSS)。
空间平滑技术是将等距线阵分成若干个重叠的子阵列,子阵列协方差矩阵相加后取平均取代原来的Rs[10]。将M元的等距线阵用滑动方式分成L个子阵,每个子阵列有N个单元。定义第l个前向子阵的输出为[9]

(9)
其中AM为N×K维的方向矩阵,其列为N维的导向矢量aM(θi)(i=1,2,…,K)。
(10)
所以,第l个前向子阵的协方差矩阵为[9]
(11)
定义前向空间平滑协方差矩阵为
(12)
同理可得后向空间平滑协方差矩阵为
(13)
前后向平滑协方差矩阵为[11]
(14)
2.2 改进空间平滑ISS-MUSIC算法原理
在传统的平滑空间基础之上,首先把全部子阵接收数据的自相关矩阵进行互相关处理,然后对其加和平均可获得等效空间平滑矩阵[6],该方法先修正了信号协方差矩阵,再利用修正之后的空间平滑矩阵进行DOA估计。改进后的空间平滑算法拥有更好的分辨力。改进ISS算法的等效空间平滑矩阵为
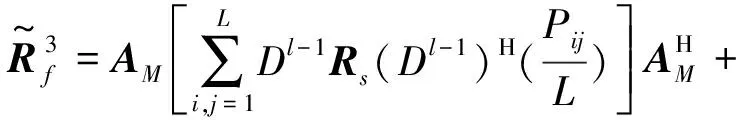
(15)
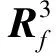
(16)
2.3 算法性能分析
由以上原理分析可知,改进的空间平滑ISS-MUSIC能够更多地增加等效平滑空间中的信号信息,同时降低了噪声的影响[6]。在利用信息的角度来看,常规的平滑MUSIC利用了L子阵的自相关信息,ISS-MUSIC利用了L2个加权互相关矩阵,且进行了两次加权,充分利用了接收信息,因此,ISS-MUSIC利用了更多的运算和接收信息,实现了在低信噪比下性能的提升。
2.4 空间平滑MUSIC算法仿真分析
在表1的条件下,10°和30°信源采用相干信源,用Matlab仿真给出了双向平滑MSS-MUSIC测向结果和传统MUSIC算法的对比结果,如图3所示。
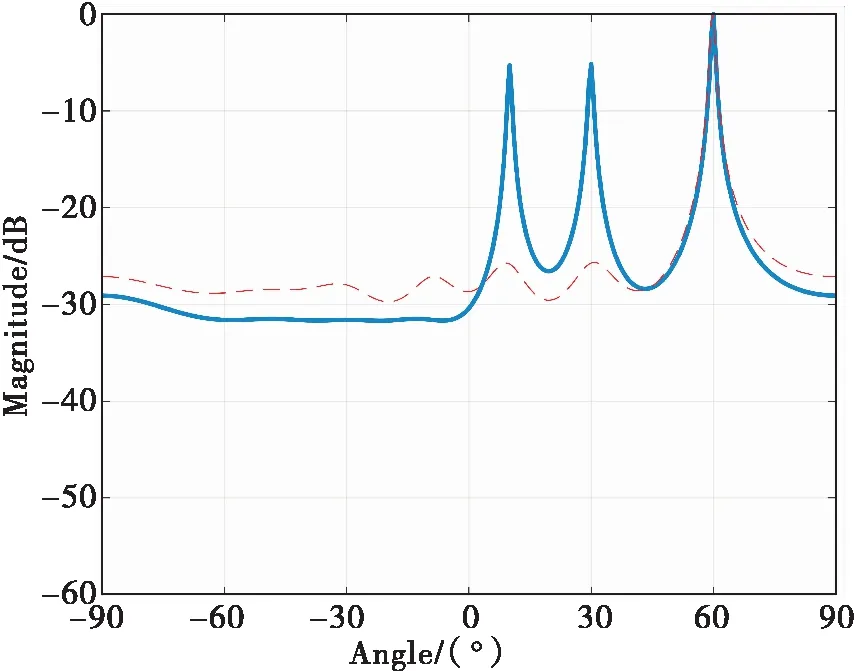
图3 MSS-MUSIC算法和MUSIC算法仿真(相干信源)
图3中,实线为MSS-MUSIC算法仿真结果,虚线为MUSIC算法仿真结果,根据图3可知,MSS-MUSIC算法可以有效地分辨相干信源。
MSS-MUSIC算法和ISS-MUSIC的对比仿真如图4和图 5所示。
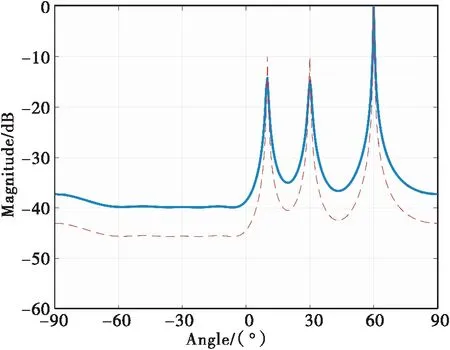
图4 MSS-MUSIC算法和ISS-MUSIC算法仿真(相干信源)

图5 MSS-MUSIC算法和ISS-MUSIC算法仿真(相干信源)
图4中虚线为ISS-MUSIC,实线为MSS-MUSIC算法仿真结果,根据结果可知,在相干信源的情况下,MSS-MUSIC算法和ISS-MUSIC算法都可以达到较好的分辨测向。采用MSS-MUSIC算法进行 DOA 估计形成的谱峰高度要比ISS-MUSIC算法形成的谱峰低,且MSS-MUSIC算法的谱峰尖锐程度也要比ISS-MUSIC算法的要粗。图5中ISS-MUSIC算法在不同信噪比下的估计误差也明显小于MSS-MUSIC算法。因此可以认为ISS-MUSIC算法处理相干信源的性能要比MSS-MUSIC优越。
3 结束语
在DOA领域中,传统的MUSIC算法可以精确地对波达方向进行估计,但其针对完全相干的两个信源时,MUSIC出现的弊端非常明显,甚至完全失去分辨能力[1]。采用平滑空间MUSIC相干源的超分辨算法,针对性解决MUSIC算法对相干信源估计失效的问题,且改进的ISS-MUSIC算法更优越。
