水电机组轴系的形状记忆合金振动控制研究

2021-10-19孙万泉郑泽知郭志强

水力发电 2021年7期

孙万泉，郑泽知，郭志强

(1.华北电力大学水利与水电工程学院，北京 102206；2. 中国电建集团海南电力设计研究院有限公司，海南海口 570100)

0 引言

水轮发电机组在运行过程中，由于水力、电磁和机械等振源的共同作用，将不可避免地产生各种振动问题，长期的不同程度的振动可能引起机组结构的变形或零部件的疲劳破环[1]。多年来国内外学者从不同角度深入研究了水轮发电机组的动力学特性及其内在机理[2]，并提出了一些有效的消振减振措施，如机组结构设计优化、补气、布置结构性装置等等。

然而，以上传统的水轮发电机组的减震措施，都是以系统线性振动方程的稳态响应为基础，并以结构最大响应为控制指标进行的。但是在实际中，由于水电站运行工况的不断变化，系统的荷载参数和结构参数等也会随之发生变化，系统的定常时不变假设已无法满足，此时系统的响应由不同工况下的稳态响应、瞬态响应和过渡过程响应等部分构成。瞬态响应和过渡过程作用时间虽短，但其幅值却往往是稳态响应的数倍。在许多工作状态下，抑制某运行工况的响应已成为保障水电站安全运行和提高效率的关键。针对该问题，传统的措施是进行运行限制，即限制机组在这一工况下运行，以避开大的振动，但这是一种不得已而为之的措施，对水电站运行的灵活调度不利。大古力水电站等即为实例，岩滩水电站和张河湾抽水蓄能电站也采用避开振动区运行方案，甚至提出超负荷运行方案。

鉴于此，提出利用新型智能材料——形状记忆合金(shape memory alloy，SMA)开展对水轮发电机组的智能振动控制研究。针对水电机组这种大质量低转速的大型旋转机械系统，由于工作介质是水，其振动特性与一般动力机械相比存在较大差异，同时引起水轮发电机组振动的原因要比普通动力机械复杂的多。因此，如何利用SMA对该大型机械进行振动控制，首先需要深入的理论研究。本文在相关SMA试验研究的基础上，建立了具有SMA控制器的水轮发电机组轴系的非线性振动模型和控制方法，实现了水轮发电机轴系在不同振源激励下的实时监测和自适应主动控制，减小机组在不同运行工况下的振动反应。该研究为水电站振动问题的解决提供了新的科学思路和方法。

1 形状记忆合金及其控制器特性

形状记忆合金(SMA)是近些年来发展起来的新型智能材料，具有独特的记忆性能、超弹性性能和高阻尼耗散性能。利用形状记忆合金超弹性效应设计的耗能器与其他的金属耗能器相比，具有耐久性和耐腐蚀性能好，使用周期长，允许大变形并且变形可恢复等一系列优点。文献[3]在Graesser & Cozzarelli模型的基础上提出了考虑SMA大应变特性的修正本构模型。文献[4]采用模糊控制器改变SMA的参数，证明基于SMA智能阻尼器的模糊控制可以有效降低结构位移和加速度幅值，提高结构抗震能力。文献[5]设计了一种拉压型SMA阻尼器，研究验证了SMA阻尼器对长拉索有明显的减振效果。

利用SMA的超弹性特性，可以开发各种型式的耗能阻尼器，以控制和减轻结构的振动。Craesser & Cozzarelli模型[6]描述了小应变情况下SMA特性，而在大应变下SMA马氏体的硬化特性不能得到描述。针对水轮发电机组安装的SMA控制器可能出现大应变的情况，本文SMA控制器采用了改进的Craesser & Cozzarelli模型[3]，其微分形式为

(1)

其中

(2)

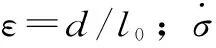
通过式(1)、(2)得到的SMA控制器恢复力—位移滞回曲线(见图1)和式(3)，求得SMA等效刚度Ke和等效阻尼系数Cv，再经由“Kelvin-Voigt”模型[4]可求得控制器提供恢复力并应用到机组轴系振动运动方程中，“Kelvin-Voigt”模型为

(3)

(4)

根据相关SMA材料的试验结果[3]，SMA控制器的参数取值如下：E=39 500 MPa，非弹性范围内斜率Ey=360 MPa，n=3，fT=0.5，c=0.001，a=550，fM=10 000，m=3，εMf=3%，Y=385 MPa，l0=200 mm。假设控制器采用2根SMA丝和4根SMA丝，由式(1)计算的滞回曲线如图1所示。可以看出，采用4根SMA丝比采用两根SMA丝时的控制器在最大位移下提供的恢复力高出一倍。因此，可根据系统振动特性选择控制器中SMA丝的控制数目和调节控制力大小。

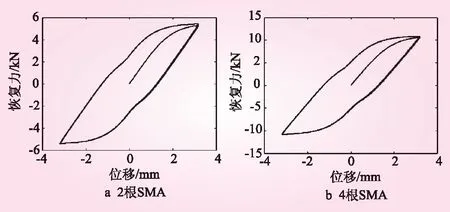
图1 不同SMA丝数目下控制器恢复力-位移曲线

2 水轮发电机组轴系统不同振动状态下的SMA主动控制

水轮发电机组轴系统出现振动故障，其原因可能是单一振源引起，也可能是多个振源耦合作用的结果。为此，本文分别就不平衡磁拉力作为单一激励引起的振动[7]，以及不平衡磁拉力与转轮的非线性密封力作为耦合激励引起的振动问题进行研究。

2.1 SMA智能振动控制原理

将SMA控制器安装在水轮发电机轴系结构中，通过收集正常振动信号和故障振动信号建立起故障识别数据库，将实际振动情况与数据库中的数据进行对比，从而确定系统是否出现非正常振动情况，之后通过对SMA丝加热至超弹性状态以调节SMA控制器的阻尼与刚度，实现智能振动控制，其程序图如图2所示。

2.2 单一激励(不平衡磁拉力)下水轮发电机组轴系的主动控制

2.2.1 不平衡磁拉力

由于水轮发电机组磁极对数一般较多(p>3)，此时，机组的不平衡磁拉力的解析表达式为[8]

(5)

式中，Fx_ump和Fy_ump分别为x和y方向的不平衡磁拉力；R为发电机转子半径；L为转子长度；Kj为气隙基波磁动势系数，与发电机的磁极对数、匝数有关；Ij为发电机的励磁电流；μ0为空气磁导系数；γ为发电机转子转角；δ0为发电机转子不偏心时的平均气隙长度；Λn为Fourier系数。

(6)

2.2.2 基于SMA受控机组轴系非线性动力学模型

带SMA控制器的转子物理模型如图3所示，可以同时对轴系得两个方向进行控制。水轮发电机轴系结构如图4所示。

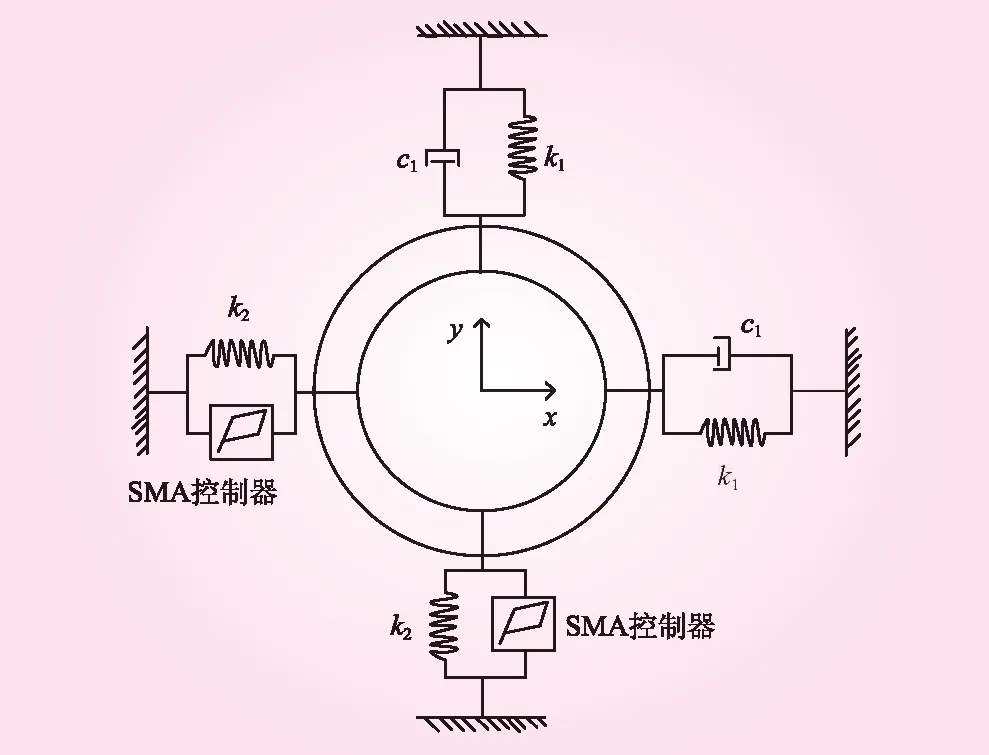
图3 带SMA控制器的转子物理模型

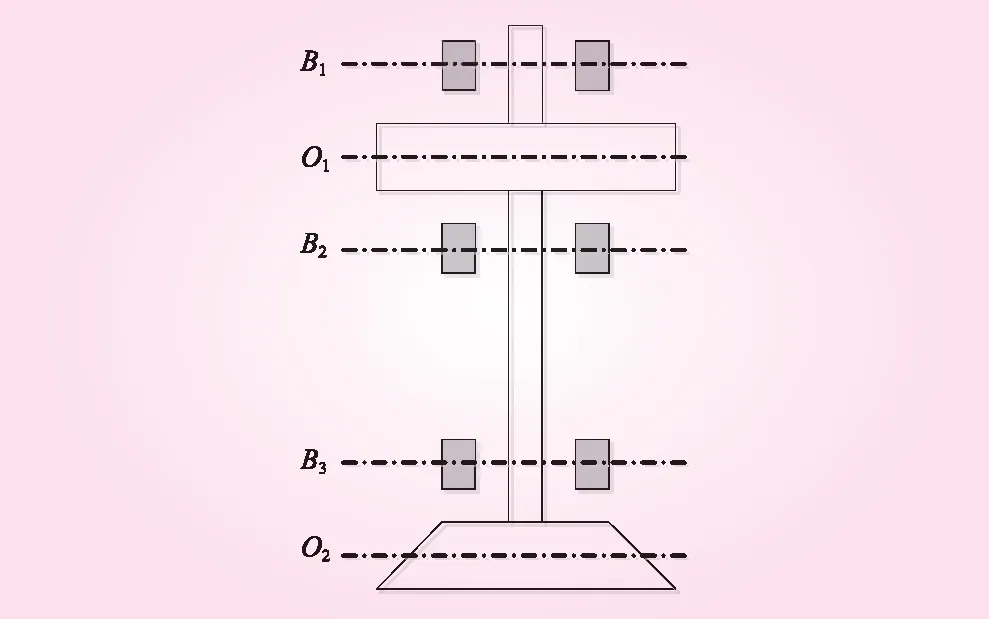
图4 水轮发电机轴系结构示意

结合式(3)、(4)，由Lagrange方程[7]可得在SMA控制器控制下的机组轴系运动微分方程

(7)

2.2.3 数值模拟

采用自适应步长的4阶、5阶龙格-库塔方法对系统进行数值仿真。参考水轮发电机技术标准[9]，选取水轮发电机组参数为：m1=1.5×104kg，m2=1.2×104kg，c1=1.5×104Ns/m，c2=1.8×104Ns/m，k1=8.5×107N/m，k2=5.8×107N/m，k3=1.8×107N/m，e1=0.5 mm，e2=0.3 mm，δ0=8 mm，μ0=4π×10-7H/m，Rr=1.2 m，Lr=0.5 m，Kj=5.1，Ij=1 090 A，机组的额定转速为ω=44.88 rad/s。SMA控制器通电加热两根SMA丝。

图5为SMA控制器控制前后发电机转子和水轮机转轮随转速变化的振动分岔示意。从图5a、5b可以看出：发电机转子径向振幅随转速的增加从0.18 mm逐渐增大，在ω=36.7 rad/s时出现小波峰，振幅达到0.8 mm，响应仍为周期运动。当转子进入相对高转速的过渡工况后(ω>52 rad/s)，转子开始进入拟周期运动，最大振幅为1.26 mm；水轮机转轮径向振幅随转速的增加先增大后减小，最大振幅为7.1 mm，发生在ω=36.7 rad/s时。同样在转轮进入相对高转速后(ω>52 rad/s)开始出现拟周期振动。

图5 单一激励下控制前后转子和转轮随转速变化的振动分岔示意

从图5c、5d可以看出：在SMA控制器施加主动控制后，转子和转轮整体振幅减小，转子径向振幅最大值减小到0.8 mm，转轮径向振幅最大值减小到0.5 mm。并且使转速较高时的复杂拟周期运动得到控制，抑制了由于不平衡磁拉力导致的振动故障，提高了机组运行的稳定性。

选取发电机转子和水轮机转轮出现拟周期运动(转速ω=52 rad/s)时的Poincaré图进行分析，如图6所示。由图6a可以看出，转子和转轮此时的吸引子均为一不规则的封闭曲线，说明此时的系统处于拟周期运动状态。在SMA控制后(图6b)，Poincaré图中的吸引子变成离散的几个点，说明水轮发电机组轴系进入稳定振动状态。

图6 主轴转速 ω=52 rad/s时控制前后转子和转轮的Poincaré图

图7显示了在相对高转速的过渡工况下，系统刚进入拟周期运动时(ω=52 rad/s)的转子转轮轴心轨迹图。由图可以看出，控制前转子和转轮轴心轨迹均呈现复杂的非对称环形，在施加控制后轴心轨迹变成了规则的圆形，转子轨迹半径由原来±1.1 mm减小到±0.5 mm，转轮轨迹半径由±1.3 mm减小到±0.5 mm。转子和转轮的振幅减小且稳定，为规律的周期运动，系统的拟周期运动得到有效控制。

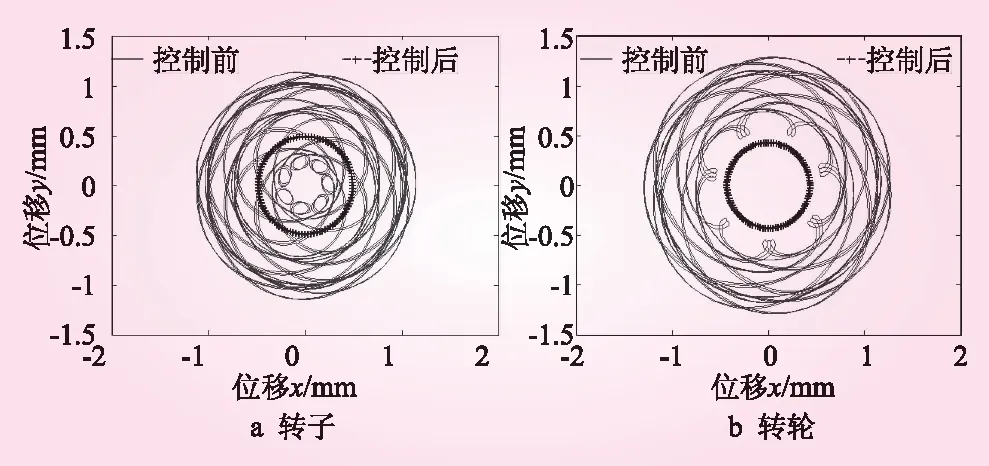
图7 主轴转速 ω=52 rad/s时控制前后轴心轨迹

2.3 耦合激励(不平衡磁拉力和密封力)下水轮发电机组轴系的主动控制

2.3.1 非线性密封力模型

受振动影响，密封体内部流场分布不均匀往往会产生不平衡力矩，从而可能引起旋转部件的自激振动，这时密封力将呈现非线性特征。国内外学者采用Muszynska密封力模型来研究非线性密封力对水轮发电机组的激振特性。Muszynska模型表达式为[8]

(8)

式中，K、D、mf分别为密封力的当量刚度、当量阻尼、当量质量。K、D、τf均为扰动位移X、Y的非线性函数[10]。

K=K0(1-e2)-n，D=D0(1-e2)-n，

τf=τ0(1-e)b，n=1/2～3，0

(9)

2.3.2 数值模拟

密封力的特性系数采用Black Childs公式计算[11]。具体计算参数为：v=3 m/s，l=0.5 m，c=2.0×10-3m，R=1.2 m，ξ=1.5，γ=1.3×10-3，n0=0.079，m0=-0.25，△P=1.5×105Pa，n=2.0，b=0.2，τ0=0.45，其余参数与上节相同。SMA控制器通电加热四根SMA丝。

图8a、8b所示为SMA控制器控制前后发电机转子和水轮机转轮随转速变化的振动分岔示意。由图8可以看出：①与单一激励相比较，在耦合激励作用下的转子和转轮会更早进入拟周期运动。②在SMA控制器施加振动控制后，机组整体运行过程的振幅都在减小。其中，在额定运行工况下，转子和转轮的最大振幅分别由0.28 mm和0.1 mm减小至0.22 mm和0.09 mm。③在相对高转速的过渡工况中，机组的复杂拟周期运动得到控制。转子和转轮的最大振幅分别由0.62 mm和0.4 mm减小至0.51 mm和0.12 mm。

图8 耦合激励下控制前后转子和转轮随转速变化的振动分岔示意

图9显示了系统刚进入拟周期运动时(ω=49 rad/s)的转子和转轮轴心轨迹。SMA丝对结构进行主动控制前后，轴心轨迹由非对称的环形带状变为规则的圆形，转子轨迹半径由±0.6 mm减小到±0.35 mm；转轮轨迹半径由±0.25 mm减小到±0.1 mm。SMA控制器使转子和转轮的拟周期运动得到有效控制。