典型城市地区小型水库溃坝洪水计算方法研究

2021-10-19卢秉彦付文博徐乙玮黄庆豪

水力发电 2021年7期

杨盼，卢路，卢秉彦，付文博，程龙，徐乙玮，黄庆豪，门亮

(1.长江水资源科学研究保护所，湖北武汉 430051；2.深圳市深水水务咨询有限公司，广东深圳 518012)

截止到2018年，我国已建98 822座水库，总库容达8 953亿m3，其中小型水库共94 132座，占比95.25%，小(2)型水库约8万座[1-3]。小型水库多为满足农业灌溉用水建于20世纪50～70年代，限于当时的技术水平不足和建设标准低，以及建成后长期缺乏规范管理养护，全国范围内水库初次安全鉴定结果表明约有4万座水库处于病险状态[4- 6]。一旦遭遇极端暴雨天气，可能存在溃坝风险。1954年～2006年间，我国共有3 498座水库溃坝，其中96.4%为小型水库，85%以上为均质土坝，漫顶和管涌是主要溃坝形式[7- 8]。1959年～1961年间和1973年左右为2个溃坝高峰期，分别溃坝507座和554座。其中，1975年8月河南省大洪水曾导致板桥和石漫滩2座大型水库、田岗和竹沟2座中型水库以及石龙山等58座小型水库溃坝[9-11]。可见，我国早期建设的小型水库遭遇历史大洪水溃坝风险极高。且我国179座城市和285座县城建有水库，城市地区人口密度大，一旦发生溃坝，将对人民生命财产安全造成重大威胁。

广东省为我国南部沿海区域，夏季降水充沛，降雨强大，已建水库8 394座，数量居全国第三；大中小型水库分别占比0.44%、4.09%和95.47%，与全国各规模水库比例基本一致[1,3]；历史溃坝近200座，溃坝数量居全国第五[7]。深圳市头陂水库建于1970年，为村民自建的灌溉农田的小型水利工程，坝型为均质土坝，2018年安全鉴定结果为三类坝，下游区域为人口密集的田心和田头社区。从建成时间、水库规模、坝型、地理位置和运用状态而言，可代表我国城市地区小型水库的普遍状态。因此，以头陂水库为例，系统全面地计算入库洪水、溃口参数、溃口流量和洪水演进过程，根据计算的淹没范围制定转移方案。可为城市地区小型水库溃坝计算提供参考。

1 工程概况

头陂水库位于深圳市坪山区的坪山河支流田头河上游，集雨面积2.20 km2，干流河长2.21 km，河流比降0.158。正常蓄水位58.00 m，死水位51.35，总库容18.95万m3，调节库容10.35万m3，死库容0.65 m3，属于五等小(2)型工程，防洪标准按30年一遇设计，300年一遇校核。工程建于1970年，是田心村村民自建的灌溉农田的小型水利工程，现转为防洪为主。水库主要建筑物包括均质土坝、开敞式宽顶堰溢洪道、输水涵等。水库大坝主要参数见表1，平面布置见图1。

表1 头陂水库大坝主要参数

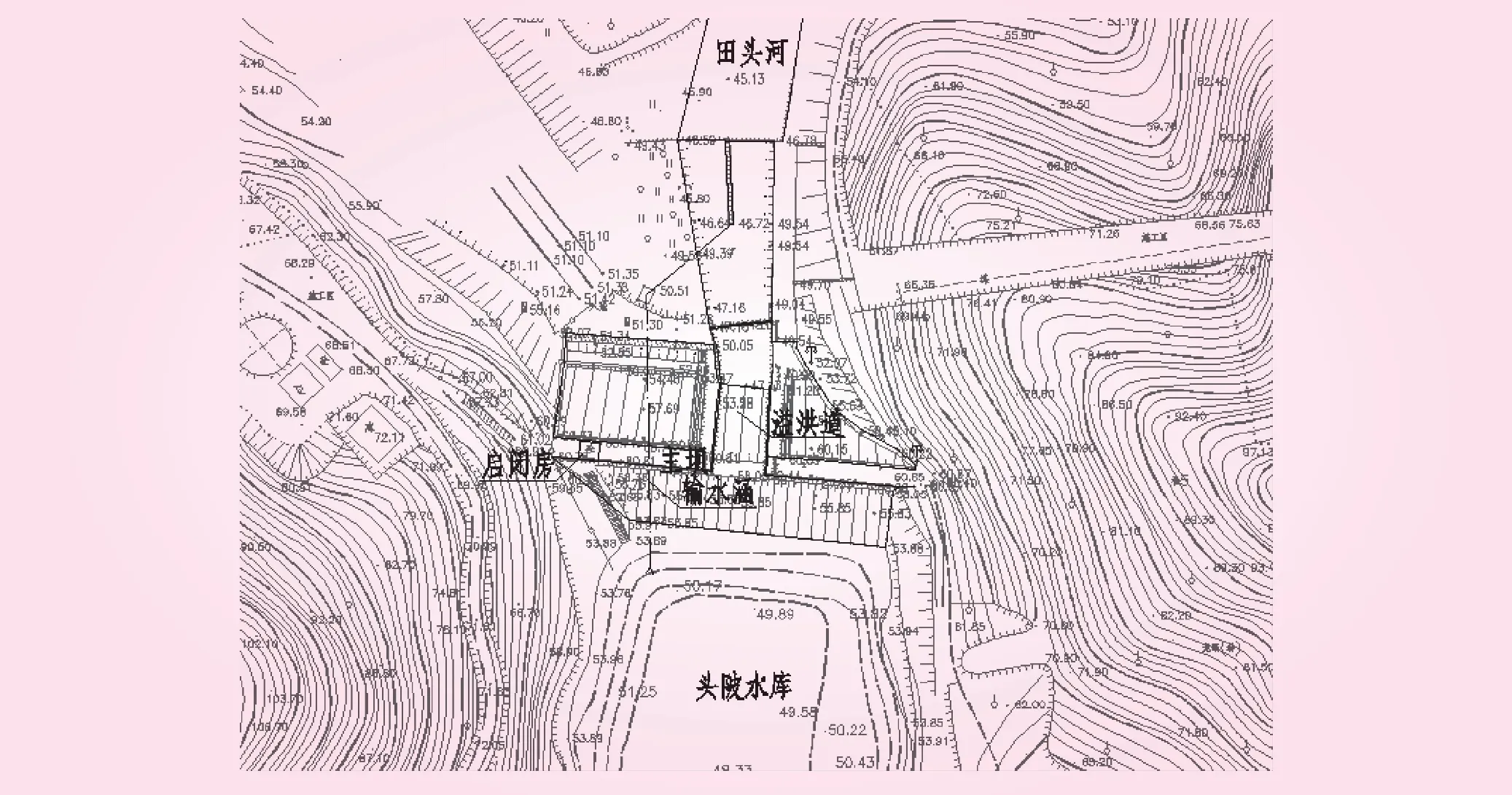
图1 头陂水库平面布置

2 计算方法

2.1 入库洪水

由于我国小型水库普遍缺乏实测洪水流量资料，故入库洪水计算采用暴雨资料推算设计洪水。采用暴雨资料推求设计洪水流量时，设计暴雨参数采用《广东省暴雨参数等值线图》(2003年版)的查算值。选取最不利工况，运用《广东省暴雨径流查算图表使用手册》中综合单位线法计算校核洪水过程线(P=0.3%)，作为引发溃坝的入库洪水。

2.2 溃口参数

相关研究表明[12-15]，土石坝溃决类型主要为逐渐局部溃决，溃口通常假定为梯形。最终溃口由以下参数确定：溃口深度hd，本次取坝高H的0.68；溃口平均宽度bm；溃口边坡s；溃口发展历时tn。采用经验公式[10，11]估算。

(1)溃口平均宽度bm，用《水力计算手册》[16]中黄河水利委员会水利科学研究院经验公式计算。

bm=kV1/4B1/4H1/2

(1)

式中，k为体材料系数，粘土类k=0.65，壤土类k=1.3；V为溃坝时蓄水量，万m3；B为坝顶长度，m；H为坝前水深，m。

(2)溃口边坡s。

(2)

(3)溃口发展历时tn。

(3)

2.3 溃坝下泄流量

溃口流量采用改进的DAMBRK模型计算。传统的DAMBRK模型计算思路为：假定溃口最终形状，从坝中间一点线性发展，不考虑坝体材料与水流相互作用过程，仅计算水库溃口流量出入变化[8, 17-19]。DAMBRK中通常建议非线性指数取值为1≤n≤4，但已有研究表明[20]，非线性参数取4时，溃坝最大流量计算值低于实测值，取6时，计算结果与实际最为接近，故本次计算取6。其中，溃口底高程ht和底宽bt发展过程计算公式如下

(4)

(5)

式中，htop为溃口顶高程，m；hbot为溃口底高程，m；t为开始溃决后时间，s；tn为溃口发展历时，s；n为非线性程度参数，本次取6；bm为最终溃口平均宽度，m。

溃口假定为梯形，下泄流量分为三角形部分Qta和矩形部分Qrt；由于头陂水库溢洪道位于坝体正中，为开敞式宽顶堰，溃口发展早期，下泄流量由溢洪道泄流量Q溢、输水涵泄流量Q涵组成。输水涵泄流量按孔口出流公式计算，其他下泄流量按堰流公式计算

Qta=cvks3.1bt(h-ht)1.5

(6)

Qrt=cvks2.45st(h-ht)2.5

(7)

Q溢=mεB溢(h-h堰)1.5

(8)

(9)

式中，h为水位，m；bt为对应时刻溃口宽度，m；ht为对应时刻溃口底高程，m；st为溃口边坡；m为堰流系数；ε为侧收缩系数；B溢为溢洪道宽度，m；h堰为溢洪道堰顶高程，m；μ为孔口流量系数；A为孔口断面面积，m2；h涵为输水涵中心高程，m；cv为水库入流收缩损失修正系数；ks为下游河流淹没修正系数，可通过下式计算得到

(10)

(11)

式中，Qt-1为上一迭代中决口的过流量，m2/s；hds为下游河道水位，m；Bd为未破坏的坝顶长度，m。

2.4 二维洪水演进

溃坝洪水演进采用二维模型MIKE21计算，以溃坝流量过程线为上边界，下边界设置为自由出流。基本方程采用平面二维浅水方程组[21-23]。其中，水流连续方程为

(12)

x方向、y方向水动力控制方程分别为

(13)

(14)

式中，t为时间，s；x、y为空间直角坐标；h为水深，m；z为自由水面水位，m，z=h+zb；zb为河床底高程；u、v为x、y方向垂向平均流速，m/s；f为科氏力系数，f=2ωsinφ；ω为地球自转角速度；φ为计算水域的地理纬度；g为重力加速度；τbx、τby分别为x、y方向的河床摩擦阻力；τsx、τsy分别为风对自由水面x、y方向的剪切力；ρ为水密度；Ex、Ey分别为x、y上的水流紊动(涡)粘性系数；S为源汇单位面积流量。

3 结果分析

3.1 计算情景设定

头陂水库2018年安全鉴定结果表明，大坝为三类坝，主要安全隐患为溢洪道边墙高度(H边墙=60.03 m)不足，遭遇设计和校核洪水(H设计=60.20 m，H校核=60.76 m)时会漫出。因此，考虑最不利工况，本次溃坝过程设定为水库遭遇校核洪水，洪水漫出溢洪道边墙冲刷下游坝坡，导致溃坝。入库洪水取校核洪水过程线区间最大6 h(见图2)，初始计算水位为正常蓄水位58.00 m，溢洪道正常运行，输水涵完全开启。起溃条件为坝前水位大于溢洪道边墙高程60.03 m，持续5 min后开始溃决。

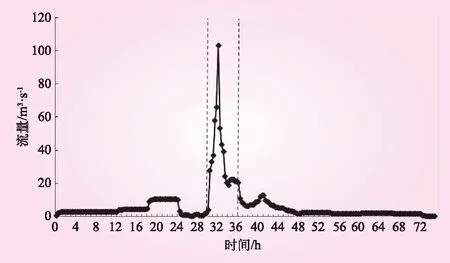
图2 校核洪水(P=0.3%)过程线

3.2 溃坝下泄流量分析

溃口发展示意如图3所示，最终溃口参数按经验公式估算，结果如下：平均宽度为13.86 m，坡比为1.4，底高程为53.73 m，发展历时为0.5 h。溃口非线性发展趋势下，溃坝总下泄流量过程线如图4所示。从图3、图4可以看出，计算开始1.6h后洪水漫出溢洪道边墙冲刷下游坝坡，持续5 min后开始溃决，溃口扩展0.5 h达到最大，此时溃口底宽3.96 m，顶宽23.76 m，边坡坡比始终为1.4。同时达到最大下泄流量313.74 m3/s。

图3 梯形溃口发展过程示意(单位: m)

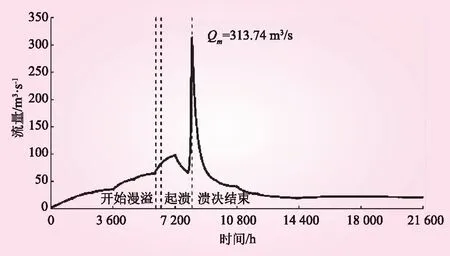
图4 溃坝下泄流量过程线

3.3 洪水演进结果分析

二维模型构建以深圳市1∶1000地形图提取的43 556 个高程点插值为地形，以溃坝下泄流量为上边界；下游洪水淹没区域地形复杂，由于缺实测资料，曼宁系数全域取20 m1/3/s；采用水量平衡率定验证，结果见表2。从表2可以看出，最大相对误差仅为3.30%，误差较小，可用于溃坝洪水淹没模拟计算。

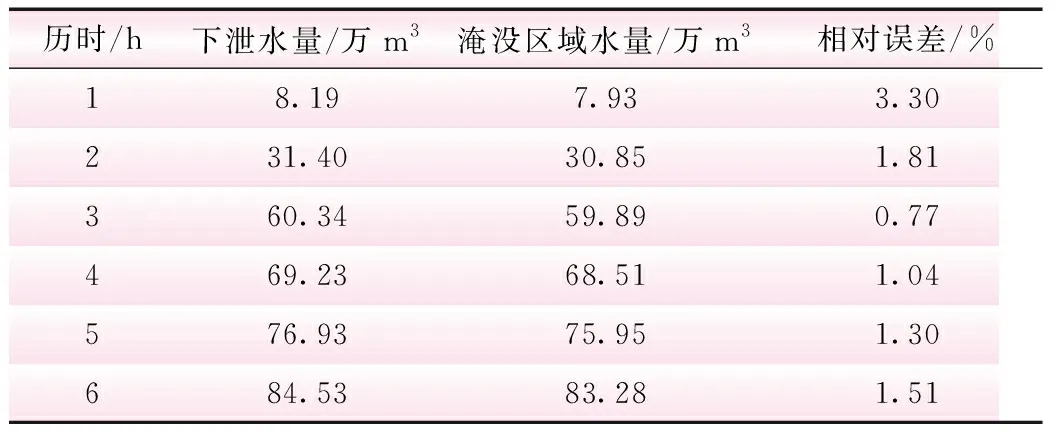
表2 水量平衡验证结果

溃坝洪水淹没范围模拟计算结果见图5。从图5可以看出，溃坝洪水主要沿2个方向演进：一个方向是沿地形较低的金田路北侧演进，淹没沿途田心社区部分民居；另一方向沿田头河方向演进，最终汇入坪山河，沿途淹没田头河两岸的新屋地村、新联村、树山背、罗古村、新区、马鞍岭等村庄。在6 h后达最大淹没面积87.51万m2，淹没范围内影响人口约3 670人。调查淹没区域周边的避难场所，制定人员转移方案。水库下游石井街道有6个室内避难场所，共能容纳1 790人，且田心社区工作站在淹没范围内，故实际能容纳人数为1 590人，剩余2 080人沿金田路、比亚迪路、坪兰路转移至大型避难场所坪山体育馆。具体路线见图6。