基于地表水-地下水耦合模型的海底地下淡水排放量估算

2021-10-19刘丙军陈晓宏

海洋科学 2021年9期

罗璐 , 俞烜 , 刘丙军 , 陈晓宏

(1. 中山大学土木工程学院, 广东珠海 519082; 2. 南方海洋科学与工程广东省实验室(珠海), 广东珠海519082)

全球有大约40%的人口和2/3的大型城市集中在沿海地区[1], 日益加剧的人类活动使得沿海地区所承受的环境压力越来越大, 近年来近海环境水污染事件如赤潮、有害藻华等也频繁发生, 这与陆源营养物质和污染物的输入密切相关[2-3]。以往的研究更多的是关注通过地表径流和大气沉降的污染物质输入, 而忽略了通过海底地下水排泄(SGD)输入的营养物质与污染物对海洋生态环境的影响。海底地下水排泄(SGD)是指不考虑流体成分、来源或驱动力,通过陆架边缘由海底进入海洋的所有流体, 主要包括陆源地下淡水排泄(submarine fresh groundwater discharge, SFGD)和再循环海水地下水排泄(submarine circulate groundwater discharge, SCGD)[4-5]。已有研究表明, SGD所携带的营养盐、有机物及其他化学物质在某些地区接近甚至超过了地表径流的输入量[6-7],SFGD作为SGD的重要组成部分, 带来大量的陆源营养物质, 是陆地向海洋输送化学物质重要且隐蔽的通道, 与沿海生态环境密切相关[8]。同时, SFGD对于某些沿海社区来说也是重要的淡水来源[5], 研究SFGD对近岸人类生活环境和生态环境具有重要影响和意义。

目前, 研究SFGD的方法主要有三种: 直接测量法、同位素示踪法和水平衡与水文模型法[9]。SFGD速率具有空间分布不均匀性, 直接测量法难以在空间和时间尺度上对SFGD速率进行展延[10], 无法进行流域或区域尺度上的估算。同位素示踪法[11-13]适用于不同尺度范围SGD的评估, 但并不能很好的解释与其总SGD相关的陆源地下淡水成分[14], 无法对研究区域进行SFGD空间分布以及时序变化分析。水平衡与水文模型法是用于估算区域SFGD速率的常用方法[15-16], 许多研究采用水文模型法对海岸SFGD进行估算时[17-18], 由于未考虑地下水与河流的交互作用, 无法反映SFGD对河流季节变化的响应规律, 由于海岸水文地质参数获取较难, 将水文耦合模型扩展应用到海岸带研究的较少[19]。随着海岸地区经济文化重要性的不断加强, 近海生态环境要求的不断提高, 进一步了解沿海流域与河口之间的水文过程, 对沿海地区陆源地下淡水排泄进行高分辨率时空估计显得愈加重要[9,20]。

本次研究利用宾州州立集成水文模型(Penn State Integrated Hydrologic Model)PIHM将地表水-地下水进行耦合, 构建海岸地表水-地下水耦合模型, 并应用于广东省东南部红海湾区域, 估计沿海流域的陆源地下淡水通量, 对SFGD速率进行时空变异分析,从而进一步了解沿海流域与河口之间相互作用的水文过程。研究基于宾州州立集成水文模型PIHM和高分辨率水文数据集, 通过模拟沿海地表、地下和海洋之间的水量交换过程, 估计流域SFGD速率, 对其空间上进行流域尺度分析、影响因素分析, 时间上进行降水响应分析, 揭示流域SFGD速率的时空变异规律。

1 研究区概况与数据来源

1.1 研究区概况

研究区域位于广东省东南部沿海, 如图1所示,其地理位置为22°42′21″～23°29′25″N, 114°57′47″～115°46′48″E, 北倚莲花山脉, 南濒南海, 从东至西依次由螺河流域片区、黄江河流域片区以及赤石河流域片区构成。区域总面积3 510 km2, 海岸线总长190 km,地势西北高东南低, 研究区内所有河流汇入南海。

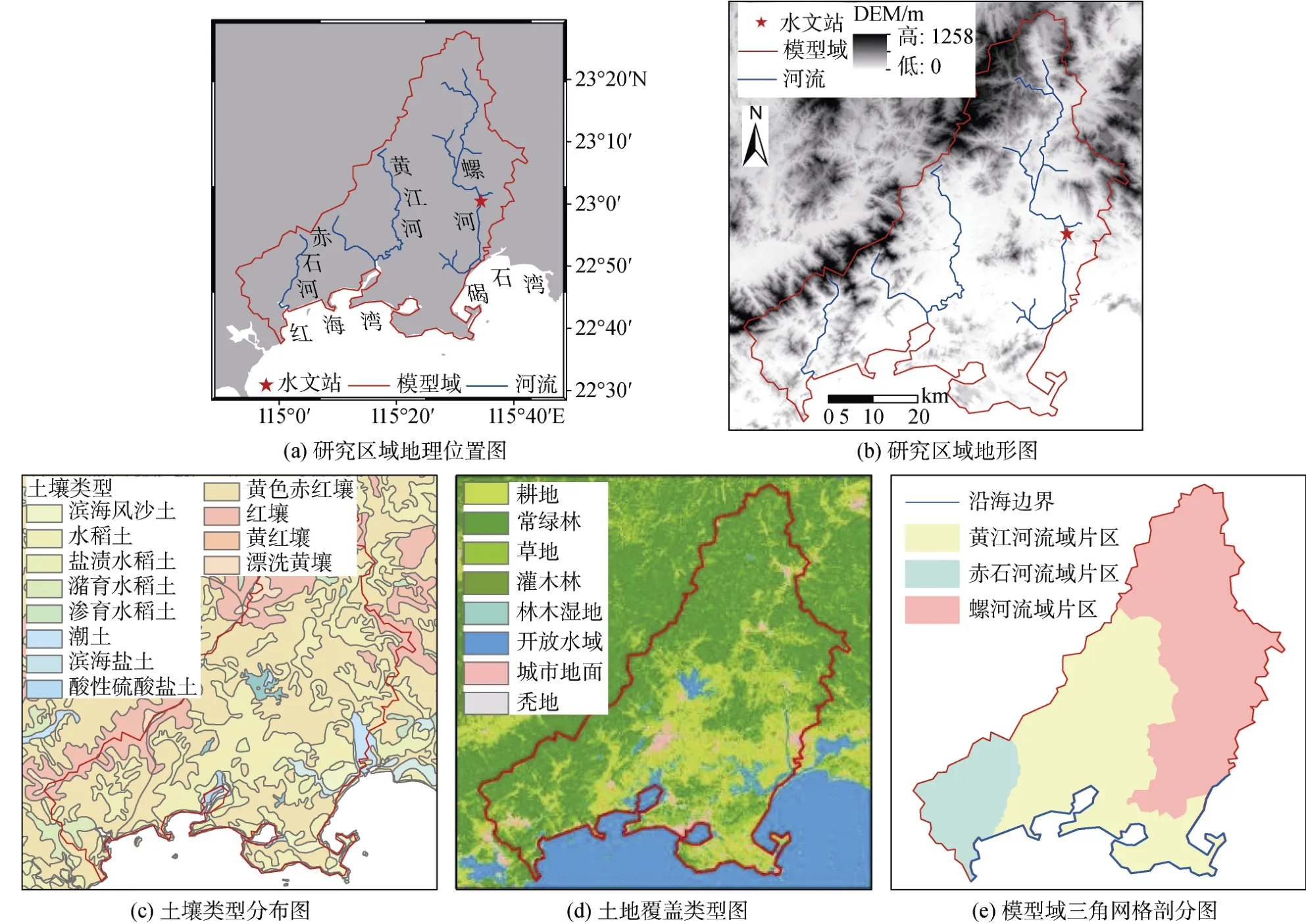
图1 研究区域概况Fig. 1 Study area

研究区属南亚热带季风气候区, 年平均降水量为1 900～2 500 mm。降雨时空分配不均匀, 空间上从西北山区向东南沿海区递减, 时间上夏多冬少,其中4月—9月(汛期)的降水占全年降水的85%以上。年平均气温为21.9 ℃[21], 全年无霜期为347 d, 年平均日照为2 179.1 h, 日照率为49%; 太阳辐射总量年平均120 kcal/cm2以上。年平均水面蒸发量为1 351.5 mm,沿海一带水面蒸发量较大, 山丘区水面蒸发量较小。研究区湿度为78%～83%。据陆丰气象站统计资料表明,年最大瞬时风速为40 m/s (风向为SE、NW), 年最大10 min平均风速为25 m/s (风向为W)。

1.2 数据来源

模型所需的基础数据包括研究区地形数据(DEM)、土地利用类型及分布信息(LUCC)、土壤属性数据库信息、水文气象资料等。

DEM数据选用30 m空间分辨率的美国国家航空航天局(NASA)的SRTM数据(http://srtm.csi.cgiar.org)。水文气象数据来自中国气象局, 主要包括日降水、日平均气温、日照、相对湿度以及风速等。模型径流模拟结果率定与验证的标准数据来自区域内唯一水文站蕉坑站2001年—2002年实测日径流量,数据系列完整连续。

本研究的土壤类型数据来源于中国科学院资源环境科学数据中心(http://www.resdc.cn)。由Pedotransfer函数[23]来估算饱和水力传导系数以及Van Genuchten持水参数α和n(表1)。

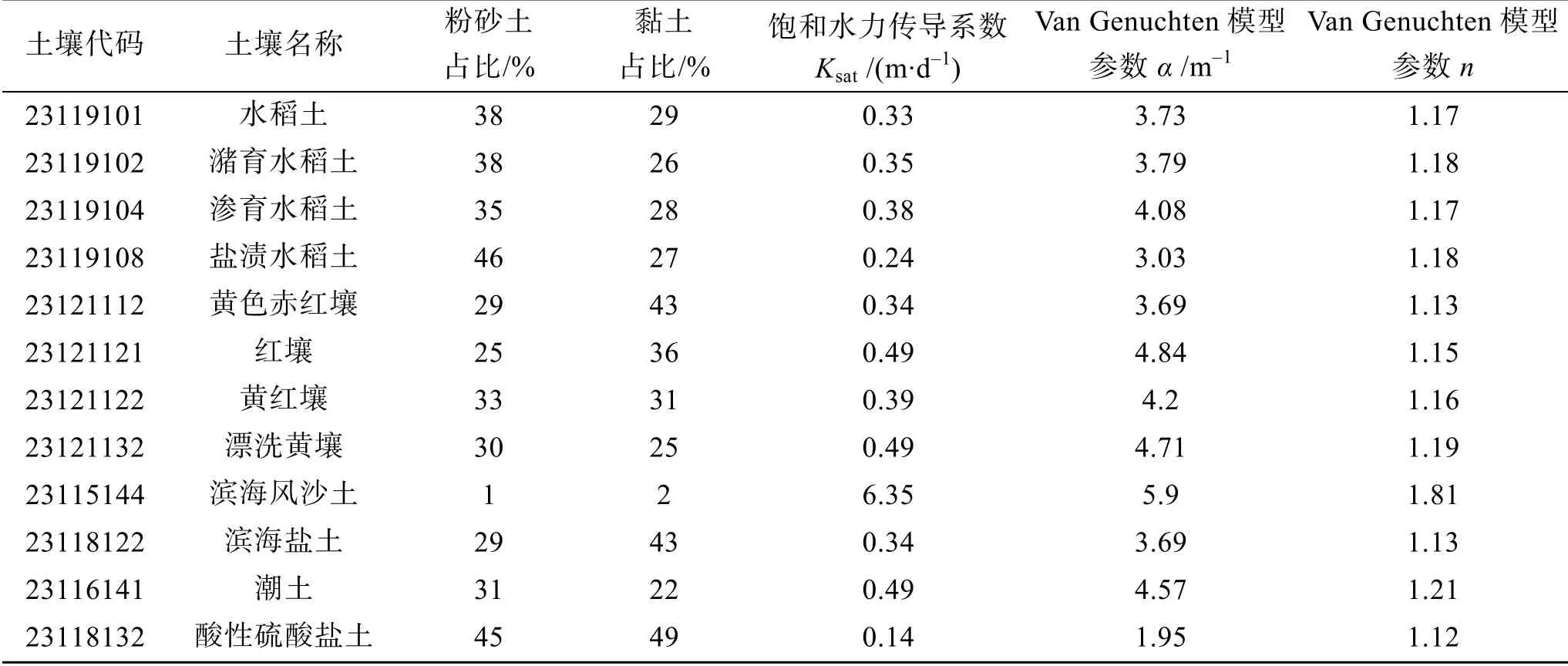
表1 研究区域土壤类型及主要参数Tab. 1 Descriptions and essential parameters of the soil types in the study area

土地利用类型选用清华大学地球科学系统研究中心2017年全球土地覆盖10 m空间分辨率数据集[24](http://data.ess.tsinghua.edu.cn/fromglc10_2017v01.html)。将土地利用类型转换为PIHM模型自带的土壤属性数据库,研究区内有8种土地覆盖类型, 包括常绿林(46.7%)、耕地(32.0%)、城市地面(6.4%)、开放水域(5.9%)、草地(5.1%)、灌木林(3.2%)、荒地(0.6%)和林木湿地(0.2%)。

2 研究方法

2.1 模型介绍

宾州州立集成水文模型PIHM是基于物理过程的、完全耦合的分布式水文模型[25], 以完全耦合的方式模拟截留、入渗、补给、蒸发蒸腾、地表径流、地下径流和河网汇流过程(图2)。区域分解受观测点、边界条件等水文特征的约束, 根据流域的地貌或水文特征, 改变流域空间离散的分辨率。每个控制体上进行水文过程建模, 包括地表径流、地下径流和渠道径流的偏微分方程, 以及叶面截留、入渗、补给和蒸散发的常微分方程。采用有限体积法将偏微分方程离散化为常微分方程, 每个网格都有对应的局部常微分方程系统, 整个研究区域组合形成一个总常微分方程系统, 使用SUNDIALS进行求解[26]。

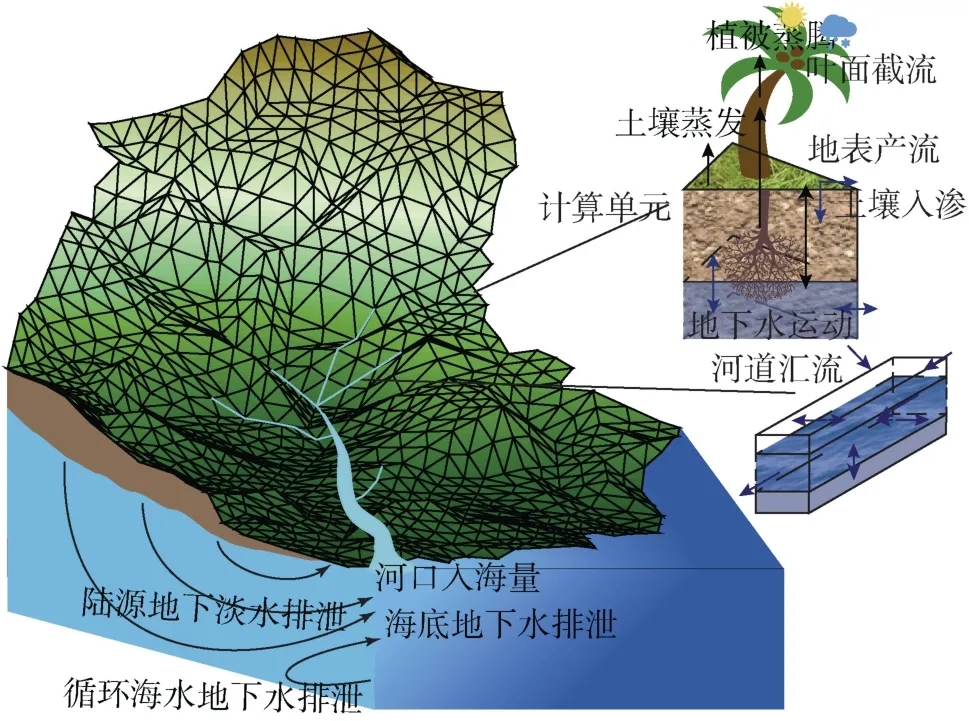
图2 PIHM模型产汇流结构Fig. 2 PennState Integrated Hydrologic Model processes

在PIHM的原始方程中, 侧重于对闭合流域进行水文模拟。通过对方程进行修改, 在流域的海岸边界处添加水头压力[27], 将海岸水文边界条件整合到模型中, 使得PIHM能够考虑海岸边界对海岸流域的影响。

2.2 基本方程

总蒸发量为林冠截留量(ec)、植被蒸腾量(et)、土壤蒸发量(es)的总和。采用Penman Monteith方程计算潜在蒸发量, 采用Noah_LSM方程来计算实际蒸散发量:

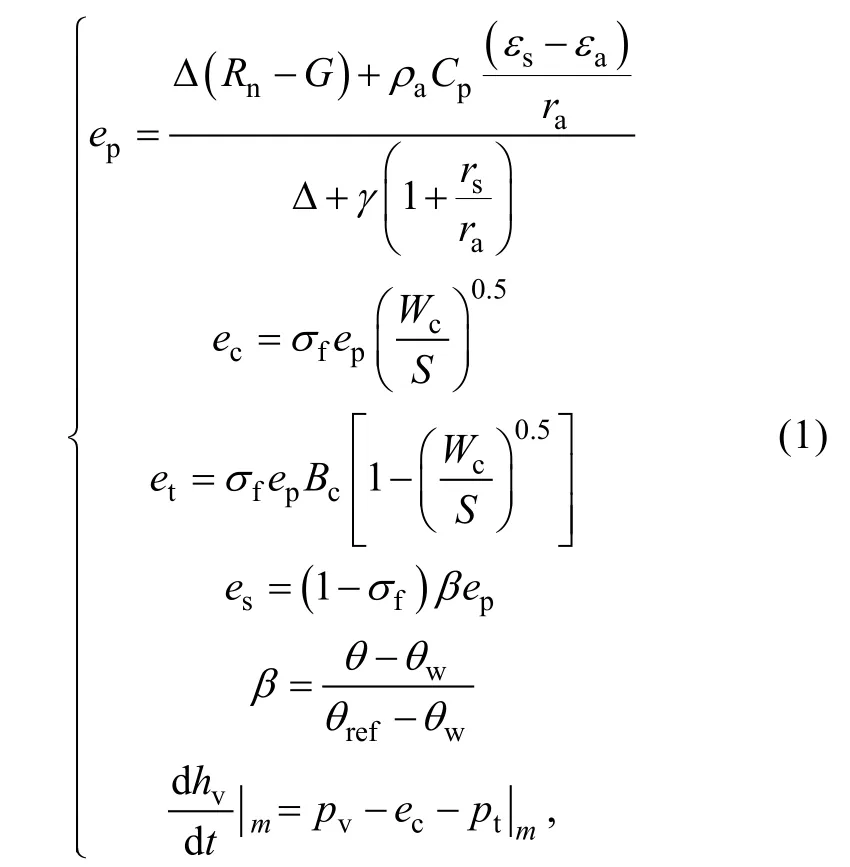
式中,ep为潜在蒸散发量;Rn为植被地表净辐射;G为土壤热通量密度;εs- εa为空气蒸汽压差额;ρa为空气密度;Cp为空气比热; Δ为饱和蒸气压-温度关系曲线的斜率;γ为计量常数;rs,ra分别为表面和空气动力阻力;σf为植被覆盖率;Wc为截冠含水量;S为最大冠层容量;Bc为冠层阻力;β为土壤水饱和度;θref为田间持水量;θw为萎蔫点;hv为植被截留量;pv为总降水量当量;pt为地表储水的入渗量和径流量; 下标m为空间网格编号, 范围从1到三角形网格总数。

赵新宇等(2013)利用吉林大学公众幸福指数课题组关于2012年中国公众主观幸福感问卷调查数据，运用有序概率模型考察了绝对收入、相对收入和预期对公众主观幸福感的影响。发现我国存在“幸福悖论”现象，相对收入对公众主观幸福感有显著促进作用，其效果强于绝对收入；预期对于中、低收入群体的主观幸福感具有显著正向作用。

使用二维Saint Venant方程来描述坡面漫流, 使用一维Saint Venant方程描述渠道径流, 使用Richard方程来描述地下径流, 用半离散方式表示为:

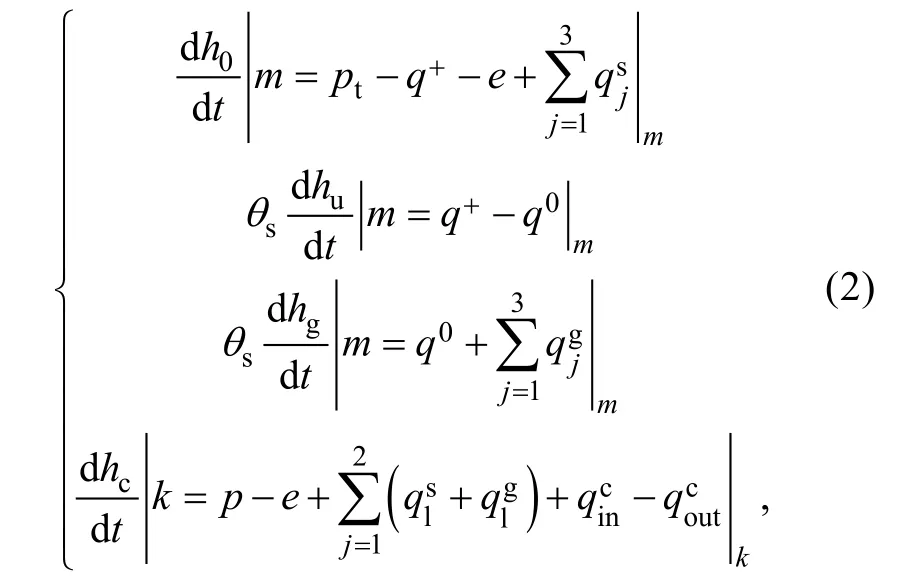
式中,h0为地表浅水深度;为元素i到相邻元素j的归一化侧向地表流量;pt、q+、e分别为净降水量、入渗量、蒸发量; 下标m为空间网格编号, 范围从1到三角形网格总数;θs为含水率;hu为非饱和地下水深度;hg为地下水深度;q0为非饱和-饱和区之间的地下水通量;为从元素i到邻近元素j的归一化侧向地下流量;hc为河道水深;p、e分别为来自河道段的降水量和蒸发量;分别为来自河道两侧的地表侧向流量和与河道相互作用的地下水流量; 各河道段的上下游流量分别为和; 下标k为河道段编号,范围从1到河道段总数。

淡水地下水通量采用以下公式进行计算[27]:

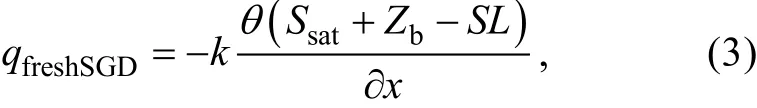
式中,qfreshSGD为淡水地下水通量, 单位m2/s;Ssat为饱和地下水储量, 单位m;Zb为基底高程, 单位m;K为水力传导系数, 单位m/d;SL为潮位高, 单位m, 设为平均海平面高度。

2.3 模型构建

用三角网格剖分法对模型进行剖分, 共得到节点6 473个, 三角形单元12 206个, 河网剖分为231条河道段。沿海岸线单元设置为定水头边界。单元平均面积约为2.88×105m2, 单元边长为500～1 000 m, 主要径流宽度为50～100 m。模型空间离散图如图1(e)所示。模拟区域初始地表水设置为0 m,初始地下水位设定为地表以下5 m, 沿海边界处的初始地下水位高程设置为0 m(平均海平面)。通过输入1992年至2014年的气象数据对研究区域的水文过程进行模拟。

3 结果与讨论

3.1 模型率定与验证

以1992年为预热期, 利用区域内唯一水文站蕉坑站2001—2002年实测日径流量, 对模型土壤及土地覆盖关键参数进行率定和验证, 选取相关系数(R)、相对误差(RE)、纳什效率系数(NSE)[28]和Kling-Gupta系数(KGE)[29]作为评价指标。R、NSE用于评估日径流过程模拟效果, RE用于分析年径流总量的模拟精度, KGE是一个集成相关系数、模拟值和实测值的均值与误差的评价指标, 用于综合反映模拟效果。关键参数包括土壤孔隙率、土壤水力参数、含水层导水率、优先流深度、河床曼宁糙率。早期模型应用提供了这些关键参数上下界的参考值[30-31]以及率定方法[26]。由于地表水-地下水耦合模拟的计算过程耗时高, 需要将参数分成两组: 产流参数组与蒸发参数组, 进行分别调参。产流参数调参选取了2001年7月1日到至7月15日的降雨径流过程, 利用CMA-ES(协方差矩阵自适应进化策略)方法进行优化。将优化结果代入后, 利用2001年水量平衡进行蒸发组参数的率定。验证期为2002年1月1日至2002年12月31日。模型率定和验证期结果见图3。

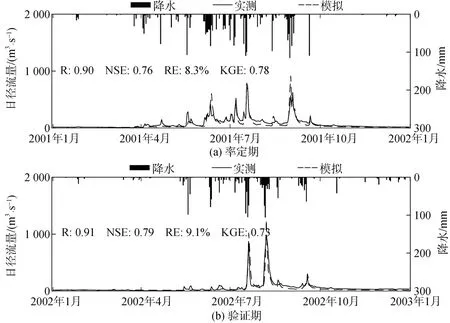
图3 蕉坑水文站实测日径流量与模拟日径流量过程Fig. 3 Observed and simulated streamflows at Jiaokeng station

图3中可以看出, 率定期和验证期模拟的日均流量过程与实测过程吻合。NSE在率定期和验证期分别为0.74和0.79,R分别为0.90和0.91, 年径流相对误差RE低于10%, KGE分别为0.78和0.73, 四个评价指标充分说明模拟满足精度要求。模型率定得到的主要参数结果见表1和表2。

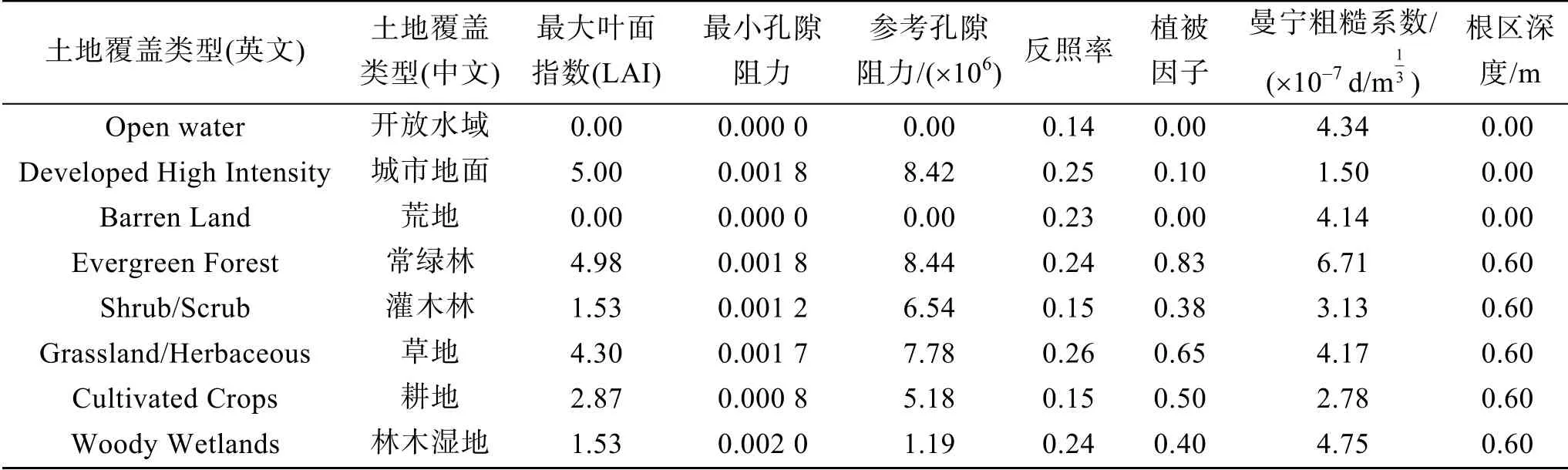
表2 研究区域土地覆盖类型及主要参数水Tab. 2 Land cover types and essential parameters in the study area

3.2 SFGD影响因素分析

在本次研究中, SFGD的影响因素主要为地形坡度(i)、渗透系数(k)以及含水层厚度(t)。模型离散化将研究区域沿海边界剖分成216段, 计算每一段边界的坡度、渗透系数、含水层厚度以及年均单位长度SFGD速率, 通过SFGD速率与各参数关系图(图4)可以看出,当i≤2%时, lg(SFGD)随i的增加而增加, 当i＞2%时,lg(SFGD)逐渐趋于稳定值。按照地形坡度是否大于2%,对SFGD速率与地形坡度(i)、渗透系数(k)以及含水层厚度(t)进行多元线性回归分析(表3)。结果显示, 当i≤2%时, lg(SFGD)与地形坡度呈极显著正相关性(P＜0.01,ri= 0.617), 与渗透系数(k)无显著相关性(P＞0.05,rk= -0.101), 与含水层厚度(t)关系不显著(P＞0.05,rt= 0.465)。表明地形坡度是SFGD速率的主控因子, 地形坡度通过影响水力坡度从而影响流向海岸的地下水,随着地形坡度的增加, SFGD速率增加。SFGD速率空间分布图(图5)显示, 地形坡度大的沿海地区SFGD速率大, 地形平缓或低洼地区SFGD速率较小。当i＞2%时, 回归模型相关系数R较小, 表明回归模型没有明显相关性, lg(SFGD)与各个自变量均无显著相关。

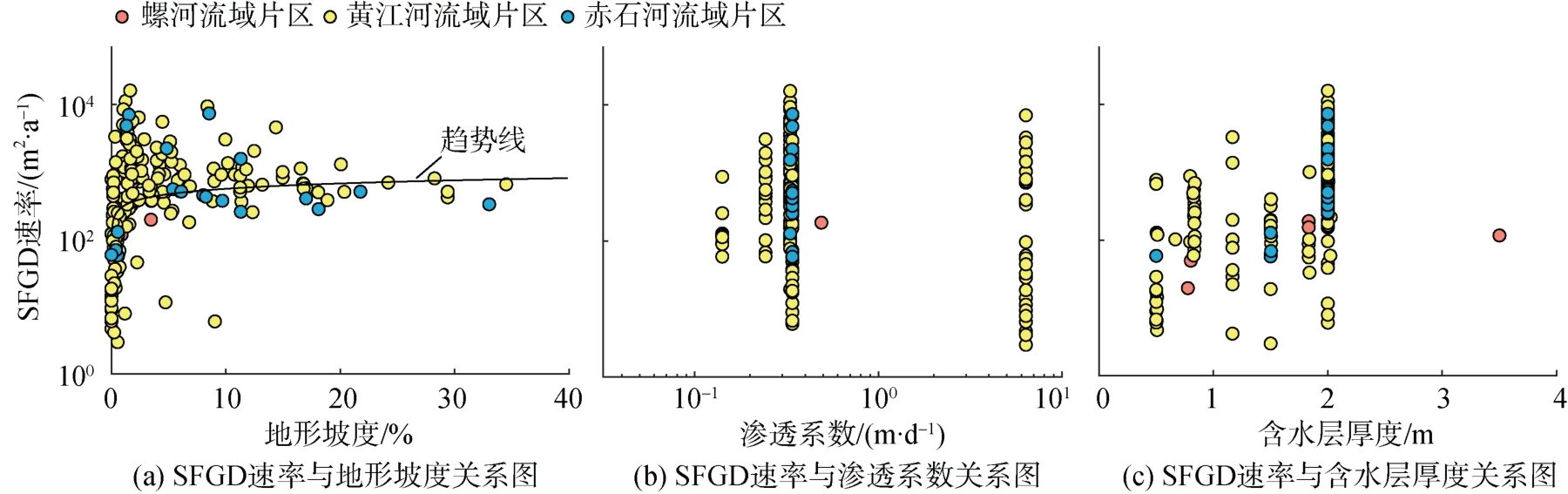
图4 模拟SFGD速率与相关水文参数关系图Fig. 4 Relationship between submarine fresh groundwater discharge (SFGD) flux and related parameters

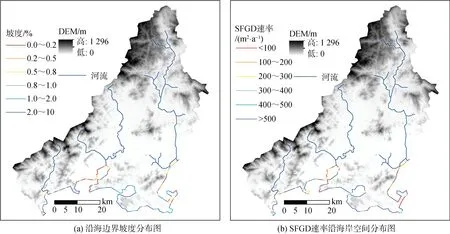
图5 SFGD速率空间分布图Fig. 5 Spatial distribution maps of SFGD

表3 lg(SFGD)多元线性回归分析系数Tab. 3 Coefficients of multiple linear regression analysis of lg(SFGD)

3.3 SFGD流域尺度分析

研究区总面积为3.51×103km2, 海岸线长190.32 km,从东至西按照主河道依次可划分为三个子流域片区,分别是螺河流域片区、黄江河流域片区和赤石河流域片区。通过分析研究区1993年—2014年共22 a的SFGD模拟结果(表4), 年平均SFGD速率为20.69×107m3/a (2.98 m2/d或0.016 1 cm/d), 占研究区内河道径流入海总量的3.28%。三个子流域中, 赤石河流域的单位长度SFGD速率最大, 为3.21 m2/d, 黄江河流域为3.05 m2/d, 与赤石河流域相近, 螺河流域的单位长度SFGD速率最小, 为0.7 m2/d, 根据4.2及4.3的分析结果, 造成这种差异的重要原因是由于三个子流域之间地形和形状的差异, 螺河流域海岸线短, 且沿海地区几乎都是平原, 地表坡度小, 因此海底地下水排泄量小。

表4 海底地下水排泄量结果统计Tab. 4 Results of submarine groundwater discharge

3.4 SFGD对降水的响应分析

统计三个子流域片区入海口处1993年—2014年间主要降水事件中地表径流峰值与SFGD通量峰值响应时间, 采用配对t检验进行分析比较(图6), 螺河流域片区、黄江河流域片区及赤石河流域片区检验的t值分别为7.638、15.426、6.603, 其双侧检验的P值均小于0.05, 表明检验结果差异显著。对比分析发现相对于地表径流, SFGD对降雨的响应更快, 平均快1～3 d。这种差异的产生可能是由于SFGD与流域地表径流的补给区不同造成的。Sawyer等[32]在对美国海岸的陆源地下淡水进行估算时, 将沿海流域依据其地貌地质划分为了不同类别的区域(图7),SFGD的补给区为径流集水区之外的向海集水区域(图7中的白色区域), 该区域内的地下水直接流向海洋。而地表径流则来源于径流集水区(图7中的灰色区域), 在本研究中, 计算的地表径流降水响应时间为流域入海口处的降水响应时间, 径流集水区的流域范围要更大, 因此其汇流时间会大于SFGD补给区的汇流时间。以上分析表明, 当发生降雨事件时,陆源地下淡水会先于地表径流达到峰值, 因此, 在沿海地区进行地下水资源管理和SFGD观测时, 需要加强监管以更快进行应对。以上分析表明, 在沿海地区进行地下水资源管理和SFGD观测时, 需要投入更多的精力以更快进行应对。

图6 地表径流峰值与SFGD峰值响应时间对比Fig. 6 Comparison between the peak values of runoff and SFGD flux

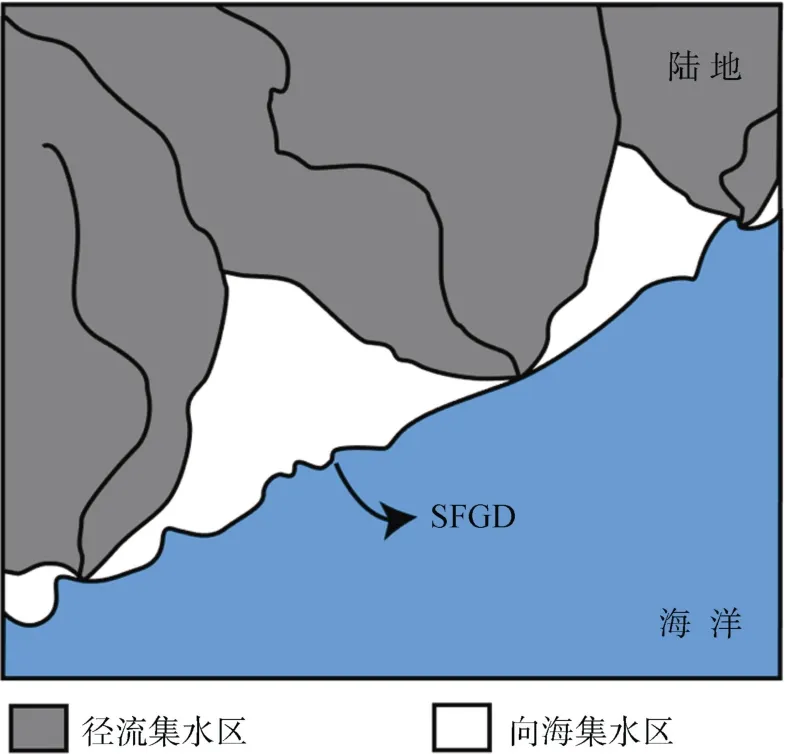
图7 SFGD补给区示意图(改自Sawyer等[32])Fig. 7 Recharge area of SFGD (modify from Sawyer et al.[32])

3.5 SFGD模拟结果比较

研究区域位于广东省东南部红海湾区域, SFGD速率为2.1×108m3/a, 该区域目前尚无SFGD评估结果可供直接比对。最近两篇估算全球海岸SFGD通量的研究中, Zhou等[18]关于研究区域的估算结果为2.4×108m3/a, 与我们的估算结果相近; Luijendijk等[17]关于研究区域的估算结果为 2.66×107(2.16×106～1.48×108) m3/a, 低于我们的评估结果。在进行全球海岸SFGD评估中, 采用的流域数据库比较粗糙, 而且由于考虑到模型计算成本, 在局部区域上会进行简化计算。本研究采用高分辨率水文气象数据集和详细的水文地质参数, 考虑了地表水-地下水交互作用,对SFGD的时空分析有更高的分辨率。

将本研究的SFGD估计值与表5中其他研究区域的SFGD估计值进行比较。为方便比较, 将单位统一为单位时间内单位海岸线长度排放量(m2/d), 即研究区域海岸线长度除SFGD排泄量。研究区的SFGD速率为2.78 m2/d, 在其他海岸SFGD评估结果范围内。沿海流域受到复杂的近海动力过程影响, 如潮汐、波浪以及海平面变化等。Kuan等[33]结合物理实验和数值模拟法研究改变内陆淡水输入以及潮汐力对海底地下水排泄的影响, 发现潮汐会通过改变淡水排泄区域宽度从而引起SFGD时间排放规律的变化; Michael等[34]的研究表明海平面上升对SFGD的影响主要取决于沿海含水层的水文地质属性, 通量控制属性(flux-controlled)的沿海含水层受到海平面上升带来的影响较小, 而水头控制属性(head-controlled)的沿海含水层则会受到较大影响。本文对研究区域近海驱动力进行简化处理, 将海岸边界设置为定水头边界, 对小时尺度的SFGD估算存在一定误差, 在日尺度及月尺度的误差影响更为明显, 将在以后的研究中进行进一步的考虑。