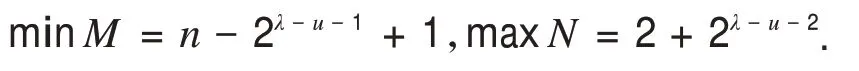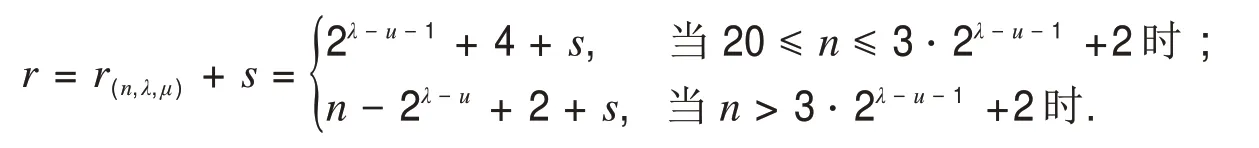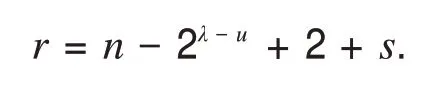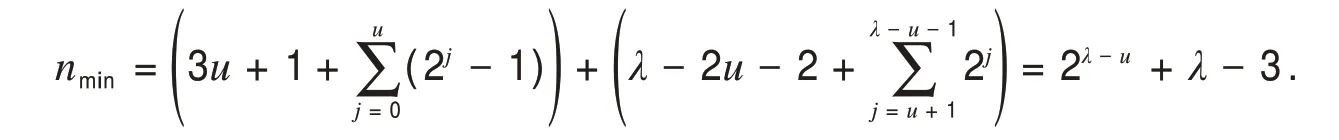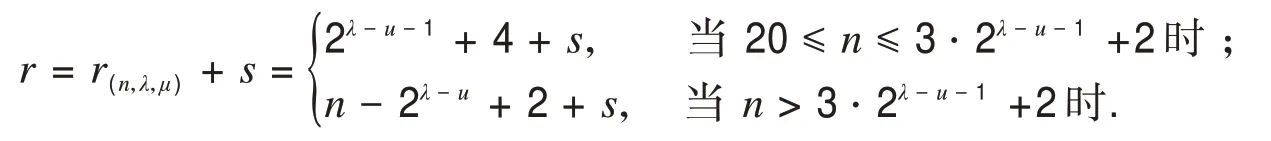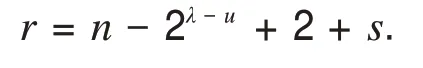一类r-(d0,d1,…,dt-1)-泛圈图的结果
2021-10-19张耀静
张耀静
(1.闽南师范大学数学与统计学院,福建漳州363000;2.数字福建气象大数据研究所,福建 漳州363000)
若n阶简单图G中长为t(3≤t≤n)的圈恰好有1 个,则称图G为唯一泛圈图.1973年,Entringer[1]提出确定唯一泛圈图的问题.1986年shi[2]证明了在n个顶点的哈密顿图中G,若所有唯一泛圈图的边数为v+m(m≤3),那么它们只有7 个,而且当边数为v+4 时,唯一泛圈图不存在,在这个基础上他提出猜想当图的边数为v+m(m≥4)时,唯一泛圈图不存在[2].2009年,Markström[3]证明了唯一泛圈图的边数的新上下界,而且还通过计算机查找证实施的猜想对点数较小的图是正确的:当阶小于或等于59 时边数v+m(m≥4)的唯一泛圈图不存在.2015年,Phillips 等[4]运用计算机发现了所有32 阶唯一偶泛圈.2016年,Wallis[5]证明了所有阶数小于30的唯一偶泛圈图.与唯一偶泛圈图的相关结果可以在文献[3,6-8]中查看.与Entringer问题相关的结果可以在文献[9-12]中查看.
若n阶简单图G中长为t(r≤t≤n)的圈恰好有k个,则称图G为r-(k)-泛圈图.2013年,Zamfirescu[13]研究了一类(2)-泛圈图并扩展到r-(2)-泛圈图,给出了r-(2)-泛圈图的定义以及构造的方法.2018年Liu[14]根据Zamfirescu[13]构造了一类r-(k)-泛圈图,并证明了r与n的关系.
1975年,Erdös[1]提出确定f(n)的问题,其中f(n)是表示没有等长圈n阶图的最大可能边数.显然可以看出Erdös问题和Entringer问题都没有等长圈.相关结果可以在文献[15-22]中查看.
若对每一个r+tj+i(r+tj+i≤n),n阶简单图G中长为r+tj+i的圈恰好有di个,0≤i≤t−1,其中t是di的周期数,j是t重复的次数,则称图G为r−(d0,…,dt−1)-泛圈图.若对每一个奇(偶)数r+tj+i(r+tj+i≤n),n阶简单图G中长为r+tj+i的圈恰好有di个,0≤i≤t−1,其中t是di的周期数,j是t重复的次数,则称图G为r−(d0,…,dt−1)-奇(偶)泛圈图.2015年陈锦丽[23]构造了一类r−(P0,P1,…,Pt−1)-泛圈图.本文主要构造了r−(6⋅2μ1,6⋅2μ1,8⋅2μ1,6⋅2μ1)-泛圈图,r−(6⋅2μ1,8⋅2μ1,6⋅2μ1,6⋅2μ1)-奇(偶)泛圈图.
1 主要结果
约定简单图G都是n阶哈密顿图,其中Cn=v1v2…vivi+1…vjvj+1…vnv1是n阶哈密顿圈.称在E(G)−E(Cn)内部区域添加的边为弦.若一对弦在Cn的内部是形如vavc与vbvd的形式,则称该对弦为交错弦,其中顶点va,vc,vb,vd不一定相邻.称vivj与vi+1vj+1(1≤i,j≤n)为一对缠绕弦(如图1所示).经过vivj,vi+1vj+1和Cn的某些边可以得到一个与Cn等长的不同圈.
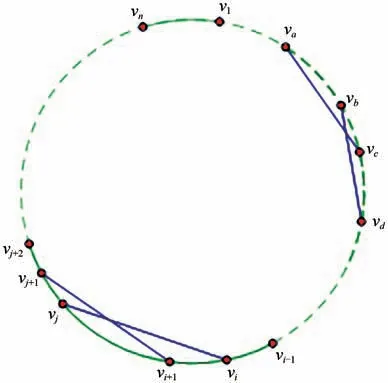
图1 泛圈图的缠绕弦与交错弦Fig.1 The interwined and staggered chord of pancyclic graph
定理1设u=u1+2,u1∈N,n≥12,λ≥6,若2λ−u−1+λ−2≤n<2λ−u+λ−1且n−r(n,λ,μ)+1 ≡s(mod4),s=0,1,2,3,那么存在一个n阶r−(6⋅2u1,6⋅2u1,8⋅2u1,6⋅2u1)-泛圈图,其中

证明(构 造法)考 虑在Cn内部添加弦:c1=v1v3,c2=v2v4,c3=v2v6,c4=v4v7,c5=v5v8,…,c2i=v2i1+2i−2v2i+2i−1,c2i+1=v2i−1+2i−1v2i+2i,其中i=2,…,u,c2u+2=v2u+2uv2u+1+2u+1,…,cλ=v2λ−u−2+2λ−2u−4v2λ−u−1+2λ−2u−3,重复这种操作,直到在Cn内部不能添加弦为止,允许cλ与v1关联,易知c1,c2跳过1个顶点,c3跳过3个顶点,当4≤j≤2u+1时,cj跳过个顶点,当2u+2≤j≤λ时,cj跳过2j−u−2个顶点.如图2.

图2 r-(6·2μ1,6·2μ1,8·2μ1,6·2μ1)-泛圈图Fig.2 The r-(6·2μ1,6·2μ1,8·2μ1,6·2μ1)-pancyclic graph
若cλ与v1关联,则

若cλ的最后的一个端点与v1之间有2λ−u−1−1个顶点,则
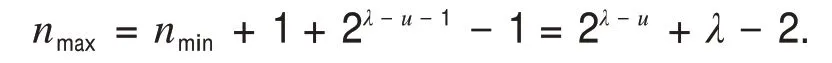
因此2λ−u−1+λ−2≤n<2λ−u+λ−1.
设Ψ 是图G的所有圈的集合.对于任一条弦,图G中恰有两个长度不等的圈仅过该弦,设Ψ0表示为G中长度较短圈及由u对缠绕弦产生的所有4圈的集合,设N为这些圈的长度的集合,
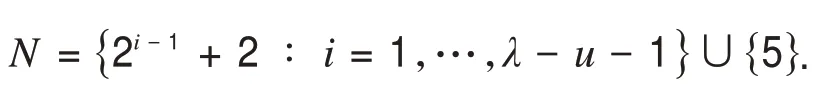
设S∈ΨΨ0,那么S必定有一条按照顺时针方向从v1到v2u+2u的路.由于在构造弦的时候,除了有u对缠绕弦,还增加一些交错弦:f1=c1c3c4,f2=c1c3c4c5,f3=c1c2c3,f4=c1c2c3c5,f5=c3c4c5,f6=c3c4,f7=c1c3c5,f8=c1c3,f9=c3c5,其中它们跳过的顶点数分别为0,0,1,1,1,1,2,2,3.
①只考虑经过缠绕弦产生的与S等长圈的个数,其中c3∉E(S).对任意的vivj,vi+1vj+1∈E(S),若vivj∈E(S),vi+1vj+1∉E(S)(vi+1vj+1∈E(S),vivj∉E(S)),那么有S'=S−vivj−vjvj+1+vivi+1+vi+1vj+1(S'=S−vivi+1−vi+1vj+1+vivj+vjvj+1),若vivj,vi+1vj+1∈E(S)(vivj∈E(S),vi+1vj+1∉E(S)),则有S'=S−vivj−vi+1vj+1+vivi+1+vjvj+1(S=S'−vivi+1−vjvj+1+vivj+vi+1vj+1),从而可知过一对缠绕弦可以产生一个与S等长的不同圈S'.对剩下的u−1 对缠绕弦类似讨论可得与S等长的圈个.
②考虑经过缠绕弦以及交错弦产生的与S1等长圈的个数,其中缠绕弦vivj,vi+1vj+1∈E(S1),8≤i ③经过c3与u−2对缠绕弦产生的与S2等长圈的个数.与①一样进行类似讨论得到经过c3与u−2对缠绕弦产生的与S2等长圈的个数为 设m∈N是ΨΨ0中圈不经过Cn的顶点的数目,m可以表示成a1⋅20+a2⋅21+…+aλ−u−12λ−u−2,其中ai=0或1,i=1,…,λ−u−1.因为c1,c2跳过1个顶点,c3跳过3个顶点,cj(4≤j≤2u+1)跳过顶点数为跳过顶点数为2j−u−2,所以0≤m≤2λ−u−1−1.设M是ΨΨ0中圈的圈长之集,那么M={n−2λ−u−1+1,…,n−2,n−1,n},从而所有的圈长之集为M∪N. 考虑r(n,λ,μ)满足r(n,λ,μ)≥minM,r(n,λ,μ)>maxN,显然有 若12≤n≤15,则r(n,λ,μ)=9. 若15 若n>3⋅2λ−u−2+2,则r(n,λ,μ)=minM=n−2λ−u−1+1. 因为在S中等长圈的数目是以4 为周期,按照6⋅2u1,6⋅2u1,8⋅2u1,6⋅2u1的形式重复出现的,所以n−r+1 ≡0(mod4),有n−r(n,λ,μ)+1+s≡0(mod4),即n−r(n,λ,μ)+1 ≡s(mod4),s=0,1,2,3.从 而 设u=u1+2,u1∈N,n≥12,λ≥6,若2λ−u−1+λ−2≤n<2λ−u+λ−1且n−r(n,λ,μ)+1 ≡s(mod4),s=0,1,2,3,那么存在一个n阶r−(6⋅2u1,6⋅2u1,8⋅2u1,6⋅2u1)-泛圈图,其中 证毕. 定理2设u=u1+2,u1∈N,n≥11,λ≥5,若2λ−u+λ−3≤n<2λ−u+1+λ−2 且n−r(n,λ,μ)+1 ≡s(mod8),s=0,2,4,6,那么 1)若n=2m,m∈N∗,则存在n阶r−(6⋅2u1,8⋅2u1,6⋅2u1,6⋅2u1)-偶泛圈图,其中 2)若n=2m+1,m∈N∗,则存在n阶r−(6⋅2u1,8⋅2u1,6⋅2u1,6⋅2u1)-奇泛圈图,其中 证明(构造法)考虑在Cn内部添加弦:c1=v1v4,c2=v2v5,c3=v3v10,c4=v5v10,c5=v6v11,…,c2i=v2i+2i−3v2i+1+2i−2,c2i+1=v2i+2i−2v2i+1+2i−1(i=2,…,μ),c2u+2=v2u+1+2u−1v2u+2+2u,…,cλ=v2λ−u−1+2λ−2u−5v2λ−u+2λ−2u−4,重复这种操作,直到在Cn内部不能添加弦为止,允许cλ与v1关联,易知c1,c2跳过2 个顶点,c3跳过6 个顶点,当4≤j≤2u+1时,cj跳过个顶点,当2u+2≤j≤λ时,cj跳过2j−u−1个顶点.如图3所示. 图3 r-(6·2μ1,8·2μ1,8·2μ1,6·2μ1)-泛圈图Fig.3 The r-(6·2μ1,8·2μ1,8·2μ1,6·2μ1)-pancyclic graph 若cλ与v1关联,则 若cλ的最后的一个端点与v1之间有2λ−u−1个顶点,则 因此2λ−u+λ−3≤n<2λ−u+1+λ−2. 设Ψ 是图G的所有圈的集合.对于任一条弦,图G中恰有两个长度不等的圈仅过该弦,设Ψ0表示为G中长度较短圈及由u对缠绕弦产生的所有4圈的集合,设N为这些圈的长度的集合, 设S∈ΨΨ0,那么S必定有一条按照顺时针方向从v1到v2u+1+2u−1的路.由于在构造弦的时候,除了有u对缠绕弦,还增加一些交错弦:f1=c2c3c5,f2=c1c2c3c5,f3=c1c3c5,f4=c3c5,f5=c2c3,f6=c1c2c3,f7=c3c4c5,f8=c1c3c4c5f9=c1c3,其中它们跳过的顶点数分别为0,0,2,2,4,4,4,4,6. ①只考虑经过缠绕弦产生的与S等长圈的个数,其中c3∉E(S).对任意的vivj,vi+1vj+1∈E(S),若vivj∈E(S),vi+1vj+1∉E(S)(vi+1vj+1∈E(S),vivj∉E(S)),那么有S'=S−vivj−vjvj+1+vivi+1+vi+1vj+1(S'=S−vivi+1−vi+1vj+1+vivj+vjvj+1),若vivj,vi+1vj+1∈E(S)(vivj∈E(S),vi+1vj+1∉E(S)),则有S'=S−vivj−vi+1vj+1+vivi+1+vjvj+1(S'=S−vivi+1−vjvj+1+vivj+vi+1vj+1),从而可知进过一对缠绕弦可以产生一个与S等长的不同圈S',对剩下的u−1 缠绕弦类似讨论可得与S等长的圈有个. ②考虑经过缠绕弦以及交错弦产生的与S1等长圈的个数,其中缠绕弦vivj,vi+1vj+1∈E(S1),8≤i ③经过c3与u−2对缠绕弦产生的与S2等长圈的个数,与①一样进行类似讨论得到经过c3与u−2对缠绕弦产生的与S2等长圈的个数为 设m∈N是ΨΨ0中圈不经过Cn的顶点的数目,m可以表示成a1⋅21+a2⋅22+…+aλ−u−12λ−u−1,其中ai=0或1,i=1,…,λ−u−1.因为c1,c2跳过2个顶点,c3跳过6个顶点,cj(4≤j≤2u+1)跳过顶点数为,cj(2u+2≤j≤λ)跳过顶点数为2j−u−1,所以0≤m≤2λ−u−2.设M是ΨΨ0中圈的圈长之集,那么M={n−2λ−u+2,…,n−2,n},从而所有的圈长之集为M∪N. 考虑r(n,λ,μ)满足r(n,λ,μ)≥minM,r(n,λ,μ)>maxN,显然有 1)当n=2m,m∈N∗时, 若20≤n≤3⋅2λ−u−1+2,则r(n,λ,μ)=2λ−u−1+4. 若n>3⋅2λ−u−1+2,则r(n,λ,μ)=n−2λ−u+2. 2)当n=2m+1,m∈N∗时,r(n,λ,μ)=n−2λ−u+2. 又因为在S中相等圈的数目是以4为周期,按照6⋅2u1,8⋅2u1,6⋅2u1,6⋅2u1的形式重复出现,即以4为周期,且在图3中所得的每个圈的长度是以2 为公差的等差数列,因此n−r+2 ≡0(mod8),故有n−r(n,λ,μ)+2+s≡0(mod8),即n−r(n,λ,μ)+2 ≡s(mod8),s=0,2,4,6.设u=u1+2,u1∈N,n≥11,λ≥5,若2λ−u+λ−3≤n<2λ−u+1+λ−2且n−r(n,λ,μ)+2 ≡s(mod8),s=0,2,4,6,那么 1)若n=2m,m∈N∗,则存在n阶r−(6⋅2u1,8⋅2u1,6⋅2u1,6⋅2u1)-偶泛圈图,其中 2)若n=2m+1,m∈N∗,则存在n阶r−(6⋅2u1,8⋅2u1,6⋅2u1,6⋅2u1)-奇泛圈图,其中 证毕.