基于相依区间值数据的EWMA FIMSE控制图
2021-10-19王美涵陈培乐潘晓映施建华
王美涵,陈培乐,潘晓映,施建华,2,3,4*
(1.闽南师范大学数学与统计学院,福建漳州363000;2.福建省粒计算及其应用重点实验室,福建漳州363000;3.福建省数据科学与统计重点实验室,福建漳州363000;4.数字福建气象大数据研究所,福建漳州363000)
在传统的统计过程控制(SPC)中,质量特征的观测值总是假设满足相互独立的要求,而当质量特征具有相依性时,传统的指数加权移动平均(EWMA)控制图发挥了良好的效果.1959年,Roberts[1]首次提出EWMA控制图,此后众多专家学者对监控过程均值变化[2]或监控过程标准差变化[3]的EWMA 控制图进行研究.而在实际生产生活中,许多情形需要同时监控过程均值和过程标准差的变化,因此一些学者提出了可以同时监控均值和标准差的EWMA控制图[4].
然而,随着测量技术的发展,越来越多的数据以相依区间值的形式来描述或记录.例如气象部门需要每小时检测一次空气中颗粒物的浓度,颗粒物残留在空气中的时间较长,这就导致了检测值是相互依赖的,即后面所检测的浓度还是会受到前面颗粒物滞留的影响.当收集到的原始数据是相依区间值数据时,就不适合应用传统的EWMA控制图来监测质量特征的变化.因此,如何设计基于相依区间值数据质量特征的控制图是一个重要而有趣的课题.
当数据是区间值数据时,传统的EWMA控制图和EWMA MSE 控制图通常是用对区间取平均值后的单一值来构建控制图,但是这样的做法有可能会丢失一些重要的信息.在质量特征具有相依性且是区间值的数据形态情况下,如何在保留相依区间值数据集的原始信息的同时,还能及时检测质量特征的变化,是质量管理的重要课题.Yang[5]评估了基于相依区间值数据的模糊相对加权移动平均(FRWMA)控制图的监控性能,发现该图的监控性能优于传统的移动平均控制图,可以更快地检测到过程均值和方差的变化.
针对相依区间值数据,模糊区间均方误差(FIMSE)作为均值偏移目标值和过程均值方差变异的综合度量,可以快速地检测到区间值数据的变异,而指数加权移动平均(EWMA)方法对全部历史数据分配了逐步减少的权重,可以快速地检测到相依数据小偏移的变异.首次将指数加权移动平均(EWMA)方法与模糊区间均方误差(FIMSE)统计量相结合,提出了基于相依区间值数据的指数加权移动平均的模糊区间均方误差(Exponentially Weighted Moving Average Fuzzy Interval Mean Square Error;EWMA FIMSE)控制图来监控过程质量特征的变化,这样可以在最大程度上保留区间数据所蕴含的信息并提高监控性能.
1 EWMA FIMSE控制图的设计
1959年,Roberts[1]首次提出EWMA控制图,其中EWMA统计量形式如下:

其中,μ为总体均值,Xˉi为样本均值,λ为平滑系数,0<λ≤1.与传统的控制图相比,它的优势在于赋予历史数据以一定的权重,距离单位时间点越近的数据权重值越大,并且随着距离单位时间点距离的增加,这种权重以指数的形式递减.EWMA控制图可以很好地应用于相依单一值数据均值的监测.
2004年,Chen[4]等提出了一种新的EWMA控制图,其统计量形式如下:

其中T∗i=(n/σ2)Ti,Ti=(Xˉi−μ)2+(n−1)S2i/n,i=1,2,…,λ为平滑系数,0<λ≤1,与EWMA控制图相比,它的优势在于可以同时监测相依单一值数据的均值和方差.
除均值和方差以外,在质量控制领域中,接近目标值也是一个值得关注的问题.1998年,Spiring 等[6]首次提出的MSE控制图可以同时监测均值和方差以及与目标值的接近程度,其中MSE统计量形式如下:

其中T为目标值,Xˉj为样本均值,S2j为样本方差.
借鉴MSE 统计量的构造,将Chen 等提出统计量中的μ用目标值T来替换,构造EWMA MSE 统计量来设计EWMA MSE 控制图,它的好处是可以同时监测相依单一值数据的均值和方差以及与目标值的接近程度.
1.1 EWMA MSE控制图
设xi1,xi2,…,xin,i=1,2,…,是来自均值为μ,方差为σ2的正态分布N(μ,σ2)的随机变量,其均方误差统计量可表示为:
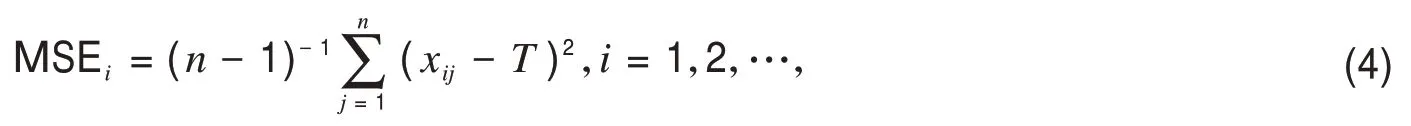
其中T为目标值,令MSE*i=(n−1)MSEi/σ2,则MSE*i统计量服从自由度为n,参数为γ=n[(μ−T)/σ]2的非中心卡方分布,即MSE*i∼,令μ−T=δ3σ,δ3>0,δ3为过程均值偏离目标值的幅度,当过程受控时,过程均值没有偏离目标值,即δ3=0时,MSE*i的均值和方差分别为:

构造EWMA MSE统计量Qi如下:
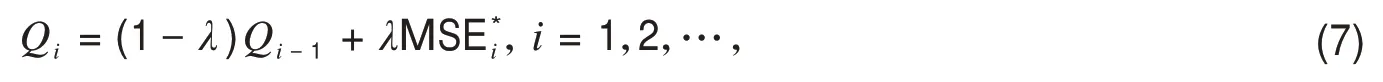
其中Q0=n+n[(μ-T)/σ]2为初始值,λ为平滑系数,0<λ≤1,当过程受控时,Qi的均值和方差分别为:

因为统计量Qi大于等于0,所以控制下限(LCL)为0,控制上限为:

其中L为控制界限系数.
1.2 EWMA FIMSE控制图
注意到,当数据为区间值数据时,上述的EWMA MSE 控制图只能将区间的最大值最小值取平均值,将区间值转化为单一值来计算,这样的方法有可能会损失大量重要的信息.为了在最大程度上保留区间值数据所蕴含的信息,首次提出EWMA FIMSE控制图,它可以同时监测相依区间值数据的均值和方差以及与目标值的接近程度.
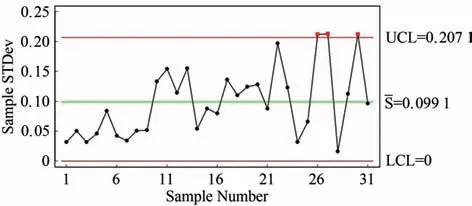
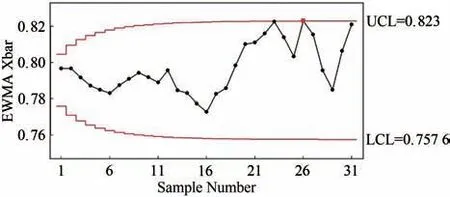
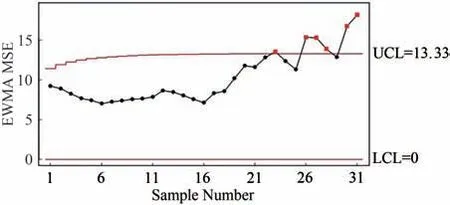
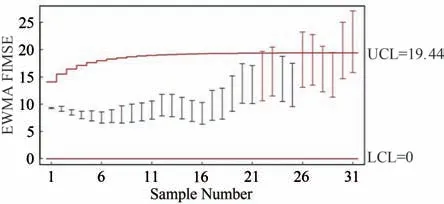
假设有一组来自均值为μ,方差为σ2的正态分布N(μ,σ2)的相依区间值随机变量序列(xi1,yi1),(xi2,yi2),…,(xin,yin),i=1,2,…,且满足关系式xin 令FIMSE1i=min(MSE1i,MSE2i),FIMSE2i=max(MSE1i,MSE2i),定义模糊区间均方误差统计量FIMSEi为: 令FIMSE*i=(n−1)FIMSEi/σ2,FIMSE*i服从参数为γ=n[(μ−T)/σ]2=nδ23,自由度为n的非中心卡方分布. 当过程受控时,FIMSE*i的均值和方差分别为: 定义EWMA FIMSE统计量FQi如下: 则 其中FQ0=[n+n[(μ−T)/σ]2,n+n[(μ−T)/σ]2]为初始值,λ为平滑系数,0<λ≤1,当过程受控时,FQi的均值和方差分别为: Wu等[7]介绍关于模糊区间变量的假设检验方法,本文借鉴该方法构建FQi的假设检验问题,设 因为统计量FQi大于等于0,且越趋于0 代表与目标值的差异越小,所以设控制下限(LCL)为0,在α的显著水平下,FQi落入拒绝域的概率函数为: 当过程受控时,控制上限为: 其中L为控制界限系数. 本节将使用蒙特卡罗模拟法来生成模糊区间值的时间序列数据,这些模糊区间值数据用于评估EW‐MA MSE控制图的平均运行长度(ARL)值,ARL指第一个质量特征落在控制界限之外时所期望的样本子组的数量,受控状态下用ARL0表示,失控状态下用ARL1表示,ARL1越小说明控制图的统计性能越好.并通过均方误差值将EWMA FIMSE 控制图的性能与传统的EWMA MSE 控制图、EWMA控制图进行比较. 计算ARL[8]的步骤如下: 1)生成一组服从均值为μ,标准差为σ的正态分布的模糊区间样本观测值. 2)利用生成的模糊区间样本观测值分别采用式(1)、式(3)、式(17)计算统计量EWMA,EWMA MSE,EWMA FIMSE. 3)利用式(21)、式(22)计算当观测统计值大于控制下限(LCL)且小于控制上限(UCL)时的ARL0,当ARL0的值近似370(固定α=0.0027,即ARL0=1/α=370)时,得到控制界限系数L的值. 4)生成一组服从均值为μ+δ1σ,δ1>0,标准差为δ2σ,δ2>1 的正态分布的模糊区间样本观测值,计算失控状态下,各观测统计值小于控制下限(LCL)和大于控制上限(UCL)时的ARL1. 表1列出了n=5,δ3=0.0 和1.0,λ=0.1,0.2 和0.3,EWMA控制图,EWMA MSE 控制图和EWMA FIMSE 控制图的ARL0近似等于370 时的控制界限系数L 的值.随着δ3的增加,EWMA FIMSE 控制图和EWMA MSE 控制图对应的L 值增加,EWMA控制图对应的L 值不变.随着λ的增加,EWMA FIMSE 控制图对应的L值减少,EWMA控制图对应的L值增加.说明EWMA FIMSE控制图和EWMA MSE控制图的控制界限系数L 的值的选取与参数δ3和λ的选取有关,EWMA控制图的控制界限系数L 的值的选取只与参数λ的选取有关. 表1 基于EWMA 、EWMA MSE、EWMA FIMSE三个控制图的ARL0Tab.1 ARL0 based on EWMA ,EWMA MSE and EWMA FIMSE control charts 表1 基于EWMA 、EWMA MSE、EWMA FIMSE三个控制图的ARL0Tab.1 ARL0 based on EWMA ,EWMA MSE and EWMA FIMSE control charts δ3 λ EWMA images/BZ_7_401_2895_442_2945.pngL 2.702 2.860 2.925 2.702 2.860 2.925 ARL0 369.9 370.1 370.4 369.9 370.1 370.4 EWMA MSE L 2.731 3.168 3.445 11.482 9.997 9.407 ARL0 370.1 370.8 370.4 370.1 369.9 370.0 0.0 1.0 0.1 0.2 0.3 0.1 0.2 0.3 EWMA FIMSE L 5.130 4.849 4.779 19.908 16.040 14.345 ARL0 370.3 370.8 369.8 370.8 370.5 369.8 表2列出了λ=0.1 时EWMA控制图、EWMA MSE 控制图和EWMA FIMSE 控制图的ARL1.显然,EWMA FIMSE 控制图的ARL1都小于EWMA MSE 控制图和EWMA控制图的ARL1,例如:当δ3=0.0,δ1=0.5,δ2=1.1 时,EWMA FIMSE 控制图的ARL1=11.83,EWMA MSE 控制图的ARL1=18.03,EWMA控制图的ARL1=26.28,这表明EWMA FIMSE 控制图比EWMA MSE 控制图和EWMA控制图更敏感,特别是当δ1和δ2取较小值时,EWMA FIMSE控制图的监测效果更好. 表2 基于EWMA 、EWMA MSE、EWMA FIMSE三个控制图的ARL1Tab.2 ARL1 based on EWMA ,EWMA MSE and EWMA FIMSE control charts 表2 基于EWMA 、EWMA MSE、EWMA FIMSE三个控制图的ARL1Tab.2 ARL1 based on EWMA ,EWMA MSE and EWMA FIMSE control charts δ3 δ1 δ2 0.1 0.0 0.5 1.0 0.1 1.0 0.5 1.0 1.1 1.3 1.5 1.1 1.3 1.5 1.1 1.3 1.5 1.1 1.3 1.5 1.1 1.3 1.5 1.1 1.3 1.5 EWMA images/BZ_7_401_2895_442_2945.png154.25 76.36 46.12 26.28 23.17 20.56 9.683 9.550 9.396 154.25 76.36 46.12 26.28 23.17 20.56 9.683 9.550 9.396 EWMA MSE 44.81 11.76 6.610 18.03 8.514 5.546 6.747 4.893 3.887 40.42 16.59 10.22 10.17 7.598 6.079 4.795 4.154 3.707 EWMA FIMSE 34.51 10.15 6.194 11.83 7.006 5.110 5.168 4.280 3.680 31.97 14.68 9.552 9.705 6.526 5.916 4.446 3.816 3.328 作为应用,搜集了漳州市2019年3月每天5 个时间段内一氧化碳(CO)的最高浓度和最低浓度的共155 个区间数据(https://quotsoft.net/air/),将其按日期分成31 组进行分析,试图检测出这个时间段的CO浓度异常的时间点.为此,分别构建EWMA控制图,EWMA MSE 控制图和EWMA FIMSE 控制图.利用S-W检验数据是否服从正态分布,算得p=0.111 2>0.05,说明数据服从正态分布. 首先,为了估计过程受控时的样本均值和标准偏差,先计算搜集的31 组区间值样本数据每个时间段CO 的最高浓度和最低浓度的均值,绘制传统的Xˉ控制图、S控制图,剔除失控的样本组.再用受控的样本组计算出过程受控时的平均值和标准偏差,计算全部的样本组的平均值和标准偏差,从而估计出偏移值然后分别计算EWMA、EWMA MSE、EWMA FIMSE 统计量的值,并分别绘制EWMA控制图、EWMA MSE控制图、EWMA FIMSE控制图. 为了计算方便,假设目标值T=0.672 1(T值可视实际需要而定),剔除Xˉ控制图和S控制图中失控的样本组26,27,28,30,31,即图1、图2中上下界外的的样本组.算得过程受控时的样本均值和标准偏差分别为=0.790 3和=0.118 2,估计的偏移值分别为 图1 控制图Fig.1 control chart 图2 S控制图Fig.2 S control chart 如图3-图5所示,在EWMA控制图、EWMA MSE控制图和EWMA FIMSE控制图中,最先被监测到出界的样本组分别为第22号、第23号和第26号,即分别在3月22日、3月23日和3月26日发现空气中CO浓度的异常.这表明,使用EWMA FIMSE 控制图来监控漳州市CO 浓度这一“质量特征”的效果要优于EWMA MSE 控制图和EWMA控制图.因此,当质量特征满足模糊相依区间值数据时,EWMA FIMSE控制图可以很好地应用于工业、经济、环境和管理领域的质量控制. 图3 EWMA 控制图Fig.3 EWMA control chart 图4 EWMA MSE控制图Fig.4 EWMA MSE control chart 图5 EWMA FIMSE控制图Fig.5 EWMA FIMSE control chart 据调查,2019年3月下旬正是春节假期结束之时,大多数企事业单位、工厂等在这段时间复工、复产,这些因素导致车流量急剧增加,汽车尾气的排放导致了CO 浓度的升高,数据分析结果从CO 的浓度异常变化角度很大程度地反映出这一社会现象,因此本文提出的方法有助于政府有关部门采取相关措施,实时监测这样的社会活动变化,做好预案. 针对具有相依性的区间值数据,提出了一种基于相依区间值数据的指数加权移动平均模糊区间均方误差(EWMA FIMSE)控制图.通过模拟和实证分析表明,所提出的EWMA FIMSE 控制图的监控性能优于传统的EWMA MSE 控制图和EWMAXˉ控制图,可以更快地监测到过程均值和方差发生较小的变化时的失控现象.除了在气象监测上的应用,也可以应用在经济、工程等领域.


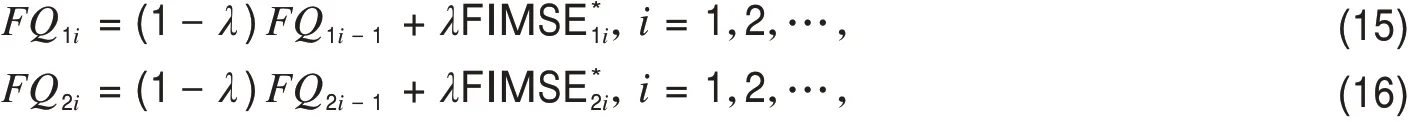





2 模拟分析


3 实证分析

4 结论
