钢骨轻骨料混凝土梁受剪性能试验与计算

朱鹏飞， 邵永健

（苏州科技大学 土木工程学院，江苏 苏州 215011）

钢骨轻骨料混凝土（SRLC）结构是一种新型结构形式，它具有承载力高、截面面积小、施工速度快、工期短、节省支模劳动力和材料，以及抗震、抗火、抗腐蚀性能优良等优点[1-2]。 SRLC 梁在大跨、高层结构中的应用日益广泛，考虑到梁的受剪破坏具有一定的突发性和危险性，因此，正确地计算其受剪承载力十分重要。

目前， 国内外学者对SRLC 梁的受剪机理进行了系统研究后认为：SRLC 梁中混凝土的受力状态与一般钢筋轻骨料混凝土梁的受力类似，而钢骨在钢筋轻骨料混凝土内部的受力状态则与纯钢结构受力不同[3-5]。文献[4]结合钢骨试验中得出的参数，用极限状态法的计算理论，在考虑轻骨料混凝土与劲性钢筋共同工作前提下，利用叠加法建立SRLC 梁斜截面受剪承载力的近似计算公式。文献[6]考虑到轻骨料混凝土强度与钢材的粘结性能较差，尺寸效应对混凝土斜截面受剪承载力的影响较大，需在钢骨普通混凝土梁斜截面受剪承载力计算公式中的混凝土项引入一个与截面尺寸有关的修正系数， 从而得到SRLC 梁斜截面受剪承载力计算公式。 文献[7]则是在SRLC 梁受剪试验的基础上，对照钢骨混凝土梁的受剪问题，提出斜截面受剪承载力计算公式。但基于上述理论提出的SRLC 梁斜截面受剪承载力计算公式均存在精度不足问题，不能很好满足工程实际需要。 研究发现，修正压力场理论[8]能描述钢筋混凝土构件在平面内剪应力和正应力作用下的力-变形反应。 文献[9-10]基于修正压力场理论对钢筋混凝土受弯构件受剪承载力进行研究。 结果表明，修正压力场理论可用于钢筋混凝土梁的受剪分析，且基于修正压力场理论建立的计算模型具有高精度的特点，能较好诠释构件的受剪机理。

本文在前人研究的基础上，通过试验来分析SRLC 梁的受剪性能，并建立其受剪承载力计算模型，进而推导出具有实际工程意义的SRLC 梁斜截面受剪承载力计算公式。

1 试验概况

1.1 试件设计与制作

试验在参照国内外SRLC 梁受剪试验的基础上，以剪跨比和轻骨料混凝土强度为主要变化参数，设计了15 根SRLC 梁和用于对比的2 根钢骨普通混凝土梁。 17 个试件的设计参数见表1 所列，试件配筋见图1。

图1 试件配筋图

表1 试验梁的设计参数

轻骨料混凝土的粗骨料选用江苏金坛海发新型建材有限公司生产的5～16 mm 连续级配的圆球型页岩陶粒，陶粒的堆积密度为865 kg/m3，表观密度为1 350 kg/m3，筒压强度为9.5 MPa，1 h 吸水率为41%，空隙率为36%；细骨料采用中砂；水泥：LC25、LC35 混凝土采用42.5 普通硅酸盐水泥，LC45、C40 混凝土采用52.5普通硅酸盐水泥；混凝土搅拌及养护用水均为城市自来水。 普通混凝土按C40 设计，其原材料除粗骨料选用5～16 mm 连续级配的碎石外，其余原材料与轻骨料混凝土的相同。

1.2 加载装置与加载制度

试验在江苏省结构工程重点实验室5 000 kN 的长柱试验机上进行，为l 点集中对称加载。 试验按《混凝土结构试验方法标准》（GB/T 50152-2012）分级加载，加载时的力学模型见图2。

图2 加载的力学模型图

1.3 测量方案与数据采集

试验主要采集各测试点的应变与挠度。应变通过DH3816 静态应变测量系统采集，应变测点的布置方式见图3。 在支座布置2 个，在梁底布置3 个位移计来读取梁的竖向变形数据，5 个位移计的布置见图4。

图3 应变片布置图

图4 位移计布置图

1.4 试验过程

试验表明，SRLC 梁在荷载作用下的受力过程经历了弹性、弹塑性和破坏三个阶段， SRLC 梁试验中各阶段的特征与其在受弯试验中表现出的特征相近。

1.5 试验结果

试验得到的l7 根试验梁的极限荷载和破坏形态见表1 所列，跨中挠度f 随荷载P 的变化曲线见图5。 由图5 可以得出：P-f 曲线不因受拉区混凝土的开裂而发生明显转折；在正常使用阶段（0.5Pu～0.7Pu），曲线基本保持线性；直到型钢屈服后，曲线开始弯曲；到达极限荷载附近时，曲线出现较为平缓的水平段。 同时，由表1 可知，剪跨比λ 对梁的破坏形态具有重要影响。 当λ＜1.5 时，发生斜压破坏；当1.5＜λ≤3.0 时,发生剪压破坏；当λ=1.5 时,可能发生斜压破坏，也可能发生剪压破坏。

图5 P-f 曲线图

2 斜截面受剪承载力的计算

对于钢骨普通混凝土梁斜截面受剪承载力的计算方法主要有三种：第一种是采用钢筋混凝土梁的计算方法，这种方法只有在钢骨含量较少时才符合实际；第二种是剪力分配法，即不考虑钢骨与混凝土之间的粘结效应，分别按钢结构和混凝土结构计算各自的受剪承载力，这种方法理论上较为合理，但计算较为复杂，剪力分配不易确定；第三种是简单叠加法，即钢骨普通混凝土梁的受剪承载力等于钢骨部分和钢筋混凝土部分受剪承载力之和，该方法计算简便。

试验发现SRLC 梁的受剪承载力基本上可以视为钢骨部分和钢筋轻骨料混凝土部分相叠加。 由此得SRLC 梁受剪承载力计算公式

式中，Vy为钢骨的受剪承载力；V'cs为钢筋轻骨料混凝土的受剪承载力。

组合结构设计规范[11]给出

式中，λ 为剪跨比；fa为钢骨抗拉设计强度；tw为腹板厚度；hw为腹板高度。

研究表明[12]，钢筋轻骨料混凝土梁的抗剪强度均低于同等级的普通混凝土梁，这主要是由轻骨料混凝土梁剪压区的受剪性能及轻骨料间的咬合力较普通混凝土差所致。 当轻骨料被剪坏时，梁截面的剪力传递能力会下降。此外，箍筋对这两种混凝土梁的影响相同。因此，对于钢筋轻骨料混凝土梁斜截面的受剪承载力计算公式可以表示为

式中，ω 为轻骨料混凝土梁抗剪强度的折减系数；Vca为钢筋混凝土构件中混凝土提供的受剪承载力；Vs为钢筋混凝土构件中箍筋提供的受剪承载力。

目前基于各类理论提出的SRLC 梁斜截面受剪承载力计算公式在精度上差距很大， 其中修正压力场理论把开裂的混凝土作为一种新型材料，由其建立的模型计算精度高。 文献[13]将钢筋混凝土构件中混凝土和箍筋提供的受剪承载力表示为

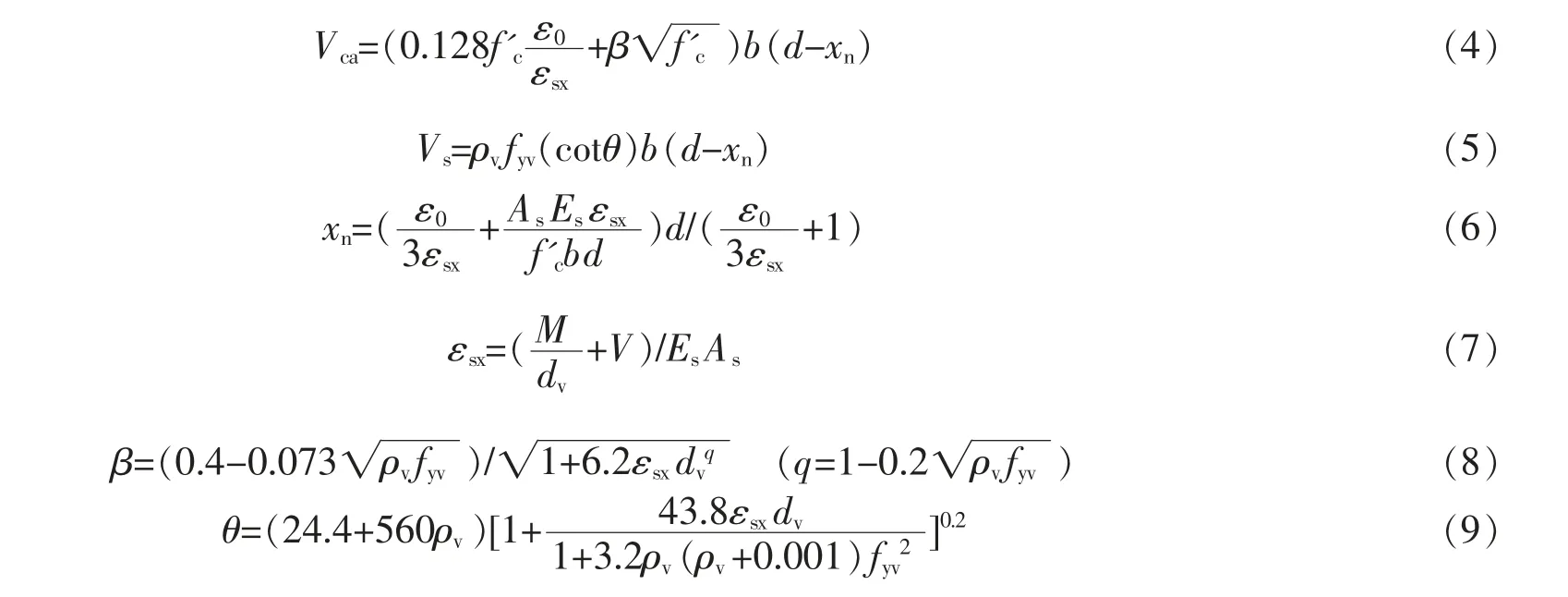
式中，f'c为混凝土圆柱体抗压强度， 取0.76fcu； fcu为混凝土立方体抗压强度实测值；ε0为峰值应力对应的应变， 取0.002；εsx为纵筋应变；b 为梁截面宽度；d 为截面有效高度；xn为中和轴高度；ρv为配箍率；fyv为箍筋屈服强度设计值；As为受拉钢筋面积；Es为钢筋弹性模量；M 为计算截面的弯矩；dv为截面受剪高度，取0.9d；V为计算截面的剪力。

综合式（1）-（5），可以得到SRLC 梁的受剪承载力计算公式

3 确定参数

由于修正压力场理论针对的是钢筋混凝土构件的纯剪状态，故本次分析使用11 根发生剪压破坏的试验梁。 基本情况如下：梁截面宽度b=200 mm，有效高度d=215 mm，立方体抗压强度fcu=31.5～52.3 MPa，混凝土圆柱体抗压强度f'c=23.94～39.75 MPa，配箍率ρv=0.09%，剪跨比λ=1.5～3.0。

3.1 求混凝土项的受剪承载力实测值V0ca

按材料强度实测值由式（2）和式（5）分别求出由钢骨承担的剪力值Vy和由箍筋承担的剪力值Vs；再根据式（1）和式（3）将试验中测得的试验梁抗剪强度V0减去Vs和Vy；即可求出混凝土项的受剪承载力实测值

3.2 求混凝土项的受剪承载力计算值Vjca

应用式（4），按材料强度实测值计算式（3）中第1 项的值, 即可求出混凝土项的受剪承载力计算值

3.3 混凝土项受剪承载力实测值V0ca 与计算值Vjca 的比较分析

当ω=1 时，混凝土项受剪承载力实测值V0ca与计算值Vjca的对比见表2 所列；当ω=0.172 时，分析见表3所列。从表2 可以看出，当ω=1 时，混凝土项受剪承载力计算值Vjca偏大，实测值V0ca与其的比值范围大致在0.1～0.3 之间，这与抗剪承载力离散性大相符，在实际应用中偏危险。 从表3 可以看出，当ω=0.172 时，混凝土项受剪承载力实测值V0ca与计算值Vjca较为接近，两者的比值集中在0.7～1.4 之间，且平均值为1.002。

表2 计算值与试验实测值的对比分析

表3 计算值与试验实测值的对比分析

考虑轻骨料对钢筋混凝土构件抗剪强度的折减效应，ω 应小于1，故取ω=0.172 时。 将其代入式（10），即可得到SRLC 梁的受剪承载力计算公式为综合国内外对钢骨轻骨料混凝土结构斜截面抗剪承载力的研究结果，考虑到试验误差与试验数据少而造成的误差及简化计算，对式（13）进行适当调整，建议SRLC 梁的受剪承载力按下列公式进行计算

4 比较分析

4.1 计算过程

根据前面推导的式（14）可对钢骨轻骨料混凝土构件进行受剪分析和设计，求解受剪承载力的步骤如下：

（1）假设计算截面的弯矩M 和剪力V；

（2）由式（7）计算纵筋应变εsx；

（3）由式（6）计算中和轴高度xn；

（4）由式（14）计算斜截面受剪承载力Vu；

（6）重复计算步骤直至求解出满足精度要求的受剪承载力。

4.2 计算结果与试验数据比较

按本文提供的方法计算试验梁的极限受剪承载力， 其与试验实测值的对比分析见表4 与表5 所列， 随剪跨比和轻骨料混凝土强度的变化规律见图6。

表4 钢骨轻骨料混凝土梁计算值与试验实测值的对比

表5 钢骨普通混凝土梁计算值与试验实测值的对比

图6 Vcalu-λ 关系

由表4 与表5 可以看出，SRLC 梁的试验结果与按本文公式计算的结果较为接近，比值基本处在0.8～1.2之间。SRLC 梁的试验结果与按本文公式计算结果比值的平均值为1.026，标准差为0.237，在SRLC 梁的受剪分析中是较为准确的。 按本文公式计算的钢骨普通混凝土梁受剪承载力与试验实测值较为接近，式（14）同样可以用于计算钢骨普通混凝土梁的受剪承载力。

由图6 可以看出，按本文公式（14）计算的SRLC 梁斜截面受剪承载力随剪跨比的增大而降低，随轻骨料混凝土强度的提高而增大，符合受剪机理。

4.3 与其他方法的比较

综合国内对钢骨轻骨料混凝土结构斜截面抗剪承载力的试验研究[4，6-7]，表6 给出了基于不同原理求解SRLC 梁受剪承载力的计算方法， 表5 的最后两列分别给出了试验结果与相应公式计算值之比的平均数和标准差，计算中混凝土强度均取试验中强度实测值。

表5 SRLC 梁受剪承载力公式的比较

由表6 可以看出，试验结果与按本文公式（14）计算结果比值的平均值接近于1 且标准差较小，说明本文基于修正压力场理论给出公式是比较准确的，误差范围小，能合理反映SRLC 梁的受剪机理。

5 结论

通过对15 根SRLC 梁和2 根钢骨普通混凝土梁受剪试验，并进行斜截面受剪承载力分析，得出结论：

（1）SRLC 试验梁受剪破坏经历了弹性、弹塑性和破坏三个阶段。 受拉区轻骨料混凝土的开裂对试验梁的刚度没有明显影响。剪跨比λ 对试验梁的破坏形态具有决定性的影响。当λ＜1.5 时，发生斜压破坏；当剪跨比1.5＜λ≤3.0 时，发生剪压破坏；当λ=1.5 时，可能发生斜压破坏，也可能发生剪压破坏。

（2）提出了SRLC 梁斜截面受剪承载力的计算公式（式（14））。 将15 根SRLC 试验梁的实测值与式（14）的计算值进行比较，发现吻合良好，说明式（14）能合理反映SRLC 梁的受剪机理。 将2 根钢骨普通混凝土试验梁的实测值与式（14）的计算值进行比较，发现计算结果与实测值较为接近，式（14）同样可以作为钢骨普通混凝土梁的斜截面受剪承载力计算公式。

（3）将提出的基于修正压力场理论提出的计算公式（式（14））与基于其他不同原理的计算方法相比较，发现本文方法精度更高，说明用修正压力场理论来诠释钢骨轻骨料混凝土构件的受剪机理可行。