基于小波阈值降噪的轴承振动信号虚假模态剔除研究

邓 婕，李舜酩，丁 瑞，王艳丰，滕光蓉

(1.南京航空航天大学 能源与动力学院， 南京 210016；2.中国航发四川燃气涡轮研究院， 四川 绵阳 621010)

当今机械系统朝着复杂化和高可靠性的趋势发展，对于机械设备的维护问题更加倾向基于设备工作状态的维护方式，即通过状态监测、故障诊断和寿命预测等方法在机械设备发生故障或即将发生故障时进行维护[1]。研究表明，机械设备中大部分故障的产生都与旋转部件密切相关[2]，因此，对旋转机械部件进行故障诊断是机械系统维护水平提高的关键。数据驱动的故障检测与诊断以其数据驱动和多变量的特点在工业实践中得到了广泛的应用[3]，这种方法通过故障信号数据训练诊断模型，提取故障特征，再通过学习的结果进行故障信号分类。作为诊断模型的输入，振动信号的质量优劣直接影响故障诊断的精度和效率，所以在信号输入诊断模型前，提高数据质量，对于其进行优化处理就显得尤为重要。

章国稳等[4]指出，当采集的振动信号噪声污染严重时，会产生大量的噪声模态，这些模态并不具备系统本身的物理特性，可以理解为虚假模态。当然，虚假模态的产生也不仅仅出现在试验的环境噪声中，常军等[5]解释了进行模态参数识别时，计算过程会产生大量的虚假模态。目前关于虚假模态剔除的研究大多集中在频域中虚假极点的自动剔除技术[6]上，这些技术或基于改进稳定图[7]，或基于聚类算法[8]等，先进行模态参数识别，再通过上述智能算法对物理模态极点进行甄别，从而提取物理极点，剔除虚假模态极点。这种方法对于后续的模态分析有很大帮助，但是由于时域信号中虚假模态成分并没有剔除，且处理过后无法得到时域信号，因此对故障诊断没有太大的参考价值。

考虑到本研究背景是为后续故障诊断服务的，在进行虚假模态剔除后仍需要得到时域信号，并且在诊断过程中不需要进行模态分析，因此本项数据优化研究着重考虑剔除由环境噪声引起的虚假模态。本文采用降噪算法处理时域信号，通过降噪前后的模态识别稳定图对比虚假模态剔除效果。传统降噪方法一般采用滤波器去除混合信号中的高频部分，保留低频部分作为有用的振动信号。这种方法在去除噪声的同时会导致高频信号失真，信号变换后的熵变大，而小波阈值降噪可以解决传统方法中的不足[9]，通过自适应的阈值处理信号分解形成的小波实现降噪效果，因此本文采用小波阈值降噪法。目前基于时域信号的模态识别方法有特征系统实现法(ERA)[10]、自然激励技术(NExT)[11]和随机子空间法(SSI)等，其中随机子空间法以其识别精度高、计算稳定性好等优势广泛应用于桥梁、车辆等工程实践中。常用的随机子空间算法可以分为3类，分别是数据驱动的随机子空间法(Data-SSI)、协方差驱动的随机子空间法(Cov-SSI)和联合随机子空间法(Comb-SSI)，刘心[12]通过仿真对比了这3种算法，发现其结果具有较高的一致性，但Cov-SSI法计算效率最高，因此本文采用Cov-SSI法进行模态识别，并通过稳定图来观察小波阈值降噪前后虚假模态出现的情况来判断该方法的正确性和有效性。

1 小波分析及降噪

通常情况下，我们采集到的振动信号都是具有噪声的，且大多数情况下可以将这些噪声当作高斯白噪声，因此被噪声污染的信号可以看作振动信号和高斯噪声的集合。在小波域中，振动信号和噪声信号所产生的小波系数是不同的，根据这个特点利用阈值函数即可去除混合信号中的噪声成分，这就是小波阈值降噪的基本原理。

小波分析是将信号分解成小波进行局域化处理，再通过信号重构进行还原的信号处理方法，其中窗口的大小和形状都可以根据实际需求进行调节，即具有自适应性的特点，小波变换自身具有多分辨率、低熵性等优势，这些特点让基于小波变换的信号降噪处理成为目前比较有效的方法，在实际应用中发挥着重要的作用。

小波分析的理论基础如下：

设函数φ(t)满足以下条件：

(1)

(2)

式中：a、b分别表示小波变换的伸缩参数和平移参数。

对于任意信号f(t)，其小波变换对为：

(3)

(4)

式中：*表示共轭。式(3)中ωf(a，b)表示信号f(t)的小波变换，式(4)为信号重构。

小波变换不同于傅里叶变换，选取不同的小波基函数，则小波变换的结果也不尽相同。通常选取小波基函数会从支撑长度、对称性、消失矩、正则性和相似性几个方面来考虑，根据不同小波基函数处理信号的特点选择合适的种类，此研究采用信号处理中比较常用的db小波系。在小波变换中，阈值和层数的选择在一定程度上对降噪效果也有较大影响。自适应阈值的选择包括以下几种：无偏风险估计阈值(rigrsure)、启发式阈值(heursure)、固定阈值(sqtwolog)和极大极小原理(minimaxi)，这些规则各有特点，对应了不同信号处理要求，要结合实际情况选择合适的阈值规则。层数选取也至关重要，当层数取值越大时，噪声信号和振动信号表现出的特性差异越大，这样更有利于二者分离，但是层数过大会导致重构信号失真。因此要进行对比衡量，选择合适的层数至关重要，本文采用3层小波启发式阈值法进行处理。3层小波分解重构算法如图1所示，信号分解为低频部分和高频部分，在低频部分进行降噪处理，信号重构时将低频处理过的信号与高频信号叠加，即图中A3、D1、D2、D3这几个部分，既能实现降噪，又保留高频成分确保信号不失真。在信号处理的角度看来，小波阈值降噪类似于低通滤波器，但由于它保留了高频有用信号特征，因此优于普通的低通滤波器。

图1 3层小波分析示意图

2 模态参数识别及可视化

随机子空间法是目前模态参数识别方法的一种，其特点在于可以直接处理时域信号，没有频率分辨率误差，不仅能准确识别振动频率，而且能很好的识别阻尼和振型。稳定图方法表征了模型阶次和模态参数之间的关系，从理论上来说，随着模态阶次的增加，真实模态会趋于稳定状态而虚假模态不稳定，通过设置阈值即可区分二者。因此本研究结合了随机子空间法和稳定图法，更好的区分振动信号中的真假模态。

2.1 协方差驱动的随机子空间法(Cov-SSI)

N自由度离散型随机状态空间模型可以表示为：

(5)

式中：输入个数为n，输出个数为l，xk∈R2n×1、yk∈Rl×1分别表示第k个时间样本对应的状态向量、输出向量；A∈R2n×2n表示离散状态矩阵;C∈Rl×2n表示离散输出矩阵;ωk∈R2n×1、νk∈Rl×1分别表示第k个时间样本的输入噪声、测量噪声。

定义输出协方差矩阵Ri：

(6)

定义状态输出协方差矩阵G：

(7)

输出协方差矩阵Ri与离散状态矩阵A、离散输出矩阵C、状态输出协方差矩阵G的关系可以表示为：

(8)

定义矩阵Yp、Yf：

(9)

(10)

式中：i和j分别表示矩阵的行数和列数；Yp的下标p表示past；Yf的下标f表示future。

构造Toeplitz矩阵：

(11)

定义观测矩阵Oi∈Ril×N和控制矩阵Mi∈RN×li，N为系统阶次，则上式可表示为：

(12)

对Toeplitz矩阵进行矩阵块分解：

(13)

式中：U1∈Rli×N；S1∈RN×N；V1∈Rli×N。

结合式(11)(12)可得：

(14)

式中：(·)+表示矩阵的伪逆。

由式(11)可知，C为Oi的前l行，G为Mi的后l列。

定义Oi的2个子矩阵T1和T2：

(15)

则离散状态矩阵A可以表示为：

(16)

系统模态参数可由离散状态矩阵A和离散输出矩阵C计算得到[13]。

2.2 稳定图

通过随机子空间法进行模态参数识别后，在稳定图中进行模态参数的可视化，则可以更加直观地分辨真假模态。稳定图是以频率为横坐标、系统阶次为纵坐标形成的散点图，其原理如图2所示，根据系统特征值两两共轭的性质可知，系统阶次必为偶数，通过判断相邻2个阶次的模态参数是否在容差范围之内，即可确定该极点是否为物理模态极点。物理模态极点在稳定图中会排列成一条纵向的直线，称为稳定轴，而噪声模态的极点则是不规则、散乱分布的[14]。

图2 稳定图原理

传统稳定图以频率和阻尼的容差作为判断极点是否稳定的依据，并没有提到振型，但是在模态比较密集的情况下，从频率上看是一阶振型，但从振型来判断却未必只有一阶[15]，因此要加入振型的判断，可以通过MAC来判定振型是否稳定，MAC值是模态置信准则，表达模态振型向量之间的相关性，计算公式如下：

(17)

改进后的稳定图对模态参数的判定可以归纳为以下3个方程：

(18)

(19)

MAC(i，i-1)>εφ

(20)

3 试验验证

通过图3所示的旋转机械故障测试试验台的滚动轴承振动信号验证所提方法的有效性，试验台设备主要包括驱动电机、联轴器、行星齿轮箱、轴承及轴承座和转盘等，各组成部件如图3(a)所示。驱动电机转速 0～1 500 r/min，增速齿轮箱的传动比为3，齿轮箱的输出转速为0～4 500 r/min。测试轴承选用HRB6208深沟球轴承，滚动轴承参数如表1所示。在轴承内圈通过线切割技术形成一个宽0.2 mm，深0.1 mm的凹槽模拟故障特征，同理制作轴承外圈裂纹故障。将故障轴承安装在右端支承轴承座内，采用加速度传感器分别获取轴承的正常工作信号及故障信号，传感器安装位置如图3(b)所示，位于轴承座中央。

图3 试验台示意图

参数内圈直径/mm外圈直径/mm滚动体直径/mm节圆直径/mm滚动体个数值4080106010

振动测试时，采样频率为12.8 kHz。小波阈值降噪选用了Matlab中的wden函数，参数设置为3层小波、软阈值，选择了db3小波。稳定图中，设置参数εf为0.05，εξ为0.1，εφ为0.98，黑色的“·”表示仅频率稳定的极点，黑色的“×”表示频率和阻尼稳定的极点，红色的“○”表示频率、阻尼和振型都稳定的点。以深沟球轴承内圈裂纹故障和外圈裂纹故障为例，用原始信号进行模态分析后的稳定图如图4(a)、图5(a)所示，经过小波阈值降噪后再进行模态分析的稳定图如图4(b)、图5(b)所示。

对比图4(a)、(b)可以看出深沟球轴承内圈振动信号特性，绿框中频率处于0～1 500 Hz的6条稳定轴在经过小波阈值降噪之后，稳定的极点个数明显增加，其稳定性特征愈发显著；蓝框中频率处于1 500～4 000 Hz区间的极点原本分布较为散乱，在经过降噪处理后能逐渐形成稳定轴，且虚假模态极点有所减少；但是在5 000 Hz左右的部分仍存在虚假极点。上文中提到，进行模态参数识别会产生虚假模态，因此通过随机子空间法进行模态参数计算，则稳定图中不可避免会存在虚假模态。但是进行模态识别只是一种可视化的方式，为了展示小波阈值降噪对于虚假模态剔除的效果，在实际进行故障诊断时并不会用到，因此这些虚假模态可以忽略。

图4 内圈裂纹故障振动信号模态分析稳定图

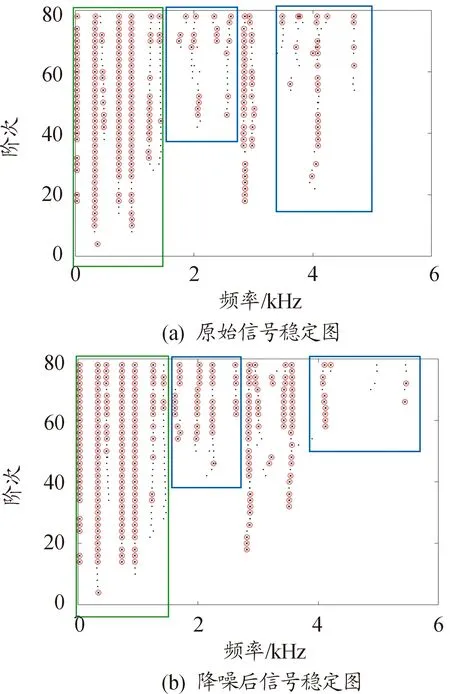
图5 外圈裂纹故障振动信号模态分析稳定图

同理深沟球轴承外圈裂纹故障振动信号也有类似的特性，对比图5(a)降噪前和图5(b)降噪后的稳定图可以看出，绿框中频率区间在0～1 500 Hz的6条稳定轴在经过小波阈值降噪之后，稳定的极点个数明显增加，其稳定性特征愈发显著；经过小波阈值降噪后，随着频率的变大，蓝框中原本分布较为散乱分散的虚假模态极点个数明显减少。通过降噪前后的稳定图对比可以看出虚假模态虽没有完全剔除，但数量相比之下有所减少，证明了小波阈值降噪对于虚假模态剔除的正确性和有效性。

4 结论

1) 采用了小波阈值法对振动信号数据进行降噪处理，以减少信号中由于环境噪声引起的虚假模态，优化振动信号数据的质量。

2) 通过随机子空间法对降噪前后的信号数据进行了模态参数识别，在稳定图中进行了可视化处理，显示出真假模态极点分布情况。

3) 对比小波阈值降噪法前后的信号模态稳定图可知，降噪后虚假模态极点数量有所减少，且真实物理模态的稳定特性更加明显，证明了所提方法的正确性和有效性，具有一定作用和应用前景。