基于变速工况稀疏调频字典的齿轮复合故障诊断

杜丽君，丁 康，蒋 飞

(华南理工大学 机械与汽车工程学院， 广州 510641)

实际生产中，齿轮不可避免地存在制造或安装误差，长期使用后容易产生磨损、断齿、轴不对中等故障，且由于齿轮箱结构复杂，内部故障难以直接观察判断。齿轮系统振动信号中蕴含着丰富的信息，故而近些年来基于振动信号分析的故障诊断方法获得了大量的关注并快速发展。

不同于传统的信号处理方法，如经验模态分解(EMD)[1]、小波变换(CT)[2]、局部均值分解(LMD)[3]、倒频谱[4]等，稀疏分解方法旨在通过构造与信号本身固有特性较为符合的字典和求解稀疏系数来重构故障特征信号，由于其在一定程度上考虑到信号本身的特性，能更有效地提取故障信号特征，学者将其用于齿轮箱的故障诊断中，取得了较好的成果。在单一故障诊断方面，Peng等[5]提出一种多尺度线调频基信号稀疏分解方法，实现了变转速下齿轮断齿故障的诊断。程军圣等[6]改进了自适应最稀疏时频分析方法，并结合阶次分析实现了变转速下齿轮断齿故障特征提取。Wang等[7-8]提出平均随机正交算法以及双增强稀疏分解方法，用于齿轮或轴承的瞬态故障提取及诊断。宋昌浩等[9]利用遗传算法优化匹配追踪的信号稀疏分解算法找出过完备字典中的最优原子，实现了齿轮箱点蚀故障的识别。Cui等[10]基于信号的特征波形构造原子库，并结合匹配追踪算法，实现了齿轮单一类型故障特征提取。李蓉等[11]将线调频基稀疏分解方法和数据驱动时频分析方法结合并应用于变转速齿轮故障诊断中。Huang[12]等利用基于振荡行为的信号分解方法，从齿轮谐波成分及其他噪声的干扰中提取出变转速下的轴承故障特征。

在复合故障诊断方面，Luo等[13]利用Laplace小波和Morlet小波字典分别表征齿轮和轴承的瞬态冲击故障，实现2种故障分离。He等[14]基于齿轮系统平稳型和冲击型故障的振动信号特征，分别建立了余弦字典和冲击响应字典，实现了齿轮箱复合故障的特征提取。Sun等[15]基于结构化稀疏时频分析方法，通过选取不同的时频邻域和广义阈值算子同时提取齿轮故障的稳态调制成分和冲击调制成分。Li等[16]综合稀疏分解理论与阶次分析，通过在角域构造准平稳调制字典及在时域构造冲击调制字典，实现了齿轮非平稳条件下分布型和局部型的复合故障诊断。

由以上可知，基于振动信号的齿轮箱故障诊断技术日趋成熟，但仍存在以下2个方面的问题：

1) 从故障类型研究方面来看，现有研究多侧重于齿轮断齿等局部型故障的诊断，较少考虑轴不对中及轮齿磨损等分布型故障以及二者耦合的复合型故障研究；

2) 从齿轮运行工况来看，研究多基于稳速工况，关于变速工况下的故障诊断研究较少。

考虑到实际工程应用中齿轮箱往往运行在变转速工况下，且箱体结构复杂，产生的故障往往并非单一类型，采集到的振动信号中常耦合了多种故障特征信息，由此提出一种针对变转速工况的齿轮箱复合故障诊断方法。所提方法基于不同类型故障信号的机理模型，构造了融合时变转速信息的时域稀疏调频字典，用于提取复合故障中的分布型故障分量，并通过冲击调制字典提取剩余信号中相对微弱的局部型故障特征，从而实现变转速工况下齿轮复合型故障的有效诊断，避免误诊与漏诊。与文献[16]所提的构造角域准平稳字典的稀疏分解方法相比，所提方法对于分布型故障成分的幅值提取更加精准，更有利于复合故障的准确诊断。

1 变转速下的齿轮箱复合故障诊断方法

1.1 变转速下齿轮复合故障信号模型

齿轮箱复合故障振动信号S(t)由分布型故障信号S1v(t)，局部型故障信号S2v(t)和高斯白噪声n(t)所组成[16]，如式(1)所示。

S(t)=S1v(t)+S2v(t)+n(t)

(1)

1.1.1分布型故障信号模型

若齿轮在制造过程中存在齿形误差、齿廓均匀磨损等缺陷，或在安装过程中有轴不对中、轴弯曲等情况时，会出现分布型故障，产生啮合调制分量。变速工况下，故障齿轮的转频随时间变化，记为fn(t)，啮合频率也随之变化，记为fm(t)，满足fm(t)=fn(t)×z。同时，故障振动信号的幅值不再是固定值，而是随转速变化。此时，齿轮分布型故障振动信号模型可以表示为S1v(t)，如式(2)所示。

(2)

(3)

式中：Azm(t)和Ank(t)表示第m阶啮合频率分量及第k阶转频调制边带的时变幅值；ρn(t)表示故障齿轮所在轴在时变转速下，不同时刻对应的角位移，由式(3)积分可得。

1.1.2局部型故障信号模型

当齿轮产生断齿、点蚀、剥落等局部型故障时，故障齿轮在啮合时会产生脉冲力，形成冲击调制分量[16]。变速工况下，冲击响应幅值和冲击间隔均随之变化，其故障振动信号模型可表示为S2v(t)，如式(4)所示。

sin[2πfd(t-Ti)]

(4)

式中：Ti为第i个冲击产生的时刻；A(Ti)为该冲击下系统响应的幅值，与Ti时刻的转速大小有关；fd和ξ为故障齿轮固有频率和阻尼比。

1.2 字典构造与稀疏系数求解

1.2.1分布型故障的稀疏调频字典构造

由变速工况下的分布型故障振动信号模型可知其频谱特征为：

1) 故障齿轮或轴的瞬时转频fn(t)及其谐波成分；

2) 以啮合频率fz(t)为载波频率，转频fn(t)为调制频率的调制边带，据此可构造如式(5)所示的调频字典：

(5)

1.2.2局部型故障的冲击字典构造

由变速工况下的局部型故障振动信号模型可知，该类型故障的振动信号由周期性的冲击响应构成，由于转速变化，各冲击发生的时间间隔不再固定。据此可构造如式(6)所示的字典：

(6)

式中：fd和ξ分别表示故障齿轮固有频率和阻尼比；τ表示每个冲击响应的发生时刻。采用相关滤波法即可获取fd和ξ的值。

稀疏系数求解方面，由于匹配追踪算法具有良好的抗噪性和稀疏表示能力[14]，本文采用该算法获得稀疏系数并进行故障信号重构。

1.2.3所提方法实施步骤

图1为所提方法的流程图，包括如下步骤：采集信号、求取转速、构造稀疏调频字典、提取分布型故障信号、构造冲击调制字典、重构局部型故障信号、故障诊断。

图1 变转速齿轮复合故障诊断流程框图

所提方法具体步骤如下：

步骤1采集变速工况下齿轮箱某测点的振动加速度信号x(t)，采样频率设为fs。

步骤2分离分布型故障信号：

① 利用文献[17]所提方法获得输入轴的瞬时转速r1(t)和转频fn1(t)，其余各轴的瞬时转频可利用传动比获得，最终得到各轴的瞬时转频集合fn(t)；

② 截取一段转频集合记为fnc(t)，该段对应的振动加速度信号记为xc(t)，按式(5)构造时域调频字典，用于表征分布型故障；

(7)

④ 采用计算阶次跟踪(COT)方法，利用输入轴转速r1(t)，将重构的时域信号xs(t)重采样到角域[16]，分析其阶次域特征，进行齿轮分布型故障诊断。

步骤3提取局部型故障信号：

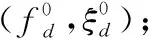
② 匹配追踪前，以转速最快的轴对应的角位移曲线对xres(t)进行分段，该轴每转一圈分一段，记每段信号为xj(t)，对应的时长为Tj，j=1，2，…，J，其中的最大时长记为Tj max，对应时间为tj max。这样划分可以避免冲击故障位于转速较低的其他齿轮上时，一个段中存在多个冲击信号；

(8)

④ 匹配追踪：对于每一段信号xj(t)xj(t)，从冲击字典Dp(tj max)中截取前Tj时长的字典，构成该段字典Dp(tj)，对该段信号进行匹配追踪，当前后残余信号均方根差小于εp时，停止迭代，重构每段信号xpj(t)，最终重构出的冲击型故障信号为xp(t)；

⑤ 对重构信号xp(t)进行阶次分析，进行齿轮局部型故障诊断。

2 仿真分析

仿真的输入轴转速曲线r(t)如图2所示，模拟齿轮箱线性升速、转速波动和准稳速运行3种工作状态。阶段1为升速过程，转速在7 s内从1 000 r/min加速到2 300 r/min；阶段2为转速波动过程，持续时间为第7～15 s；阶段3为准稳速运行过程，时间为第15～20 s。

图2 仿真转速

在该转速条件下，如式(9)所示，设置无噪声(无η(t))和有高斯白噪声(有η(t))下的2种仿真信号，模拟变速工况下，单级齿轮啮合时，存在复合型故障的振动响应信号。利用所提方法对故障信号进行重构诊断，同时对比了文献[16]所提的在角域构造准平稳调制字典提取分布型故障的方法。

x(t)=x1(t)=x2(t)+η(t)

(9)

(10)

(11)

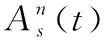
(12)

(13)

x2(t)为局部型故障仿真信号，如式(12)所示，模拟输入齿轮存在单齿的该类型故障。Ap(Ti)为第i个冲击响应的幅值，与转速r(t)有关，设Ap(Ti)=r(Ti)/8；对应时刻Ti由式(13)给出，其中初始相位φ0的取值与齿轮的故障齿所在位置有关，仿真中假设沿齿轮旋转方向的第5个齿存在故障，即故障轮齿序数m1=5，则φ0=2π/z2×(m1-1)；冲击响应的个数i由选取的信号分析时长决定；固有频率和阻尼比设定为fd=2 000，ξ=0.05。

表1 仿真信号齿轮结构参数

2.1 无噪声仿真

无噪声下，仿真信号的时域图如图3(a)所示，按1.2.3节所述方法，获得的输入轴的瞬时转速r1(t)与仿真转速r(t)的对比如图3(b)所示，2条曲线几乎重合，经计算得到二者各时刻对应的转速值最大相对误差仅为0.35%，可见获取的瞬时转速值十分接近理论值。输入轴，输出轴的转频可求得分别为fn1(t)=r1(t)/60，fn2(t)=fn1(t)×z1/z2。啮合频率最高阶次和调制边带最高阶次分别设为K=4，L=3，fn(t)={fn1(t)，fn2(t)}，相位分段数I取36，截取第3～4 s的信号作为分析对象，按照式(5)构造该时段对应的时域调频字典。

图3 仿真信号与所求转速

按1.2.3节所述方法，利用匹配追踪进行稀疏系数求解与分布型故障信号重构，设定阈值εs=0.1，最大迭代次数Nms设为每次匹配中的字典原子总个数，重构出的时域信号xs(t)如图4(a)所示，由图可知，重构信号xs(t)与原分布型故障仿真信号x1(t)十分吻合，可进一步利用相关系数(CC)值来说明xs(t)与x1(t)的匹配程度，该值越接近1表明二者的相关性越大[18]。经计算得到二者的相关系数值为0.996 5，证明了重构信号与原信号的极高匹配度，验证了该方法重构信号幅值的准确性。在如图4(b)所示的阶次谱中，各阶次成分匹配完全，可清楚看到间隔为0.56阶的调制边带，与表1中设定的故障输出齿轮的转频阶次相符合，验证了所提方法在故障特征提取与诊断方面的有效性。

图4 分布型故障重构信号与仿真信号

图5 局部型故障重构信号与仿真信号

文献[16]提出的在角域构造准平稳调制字典提取分布型故障特征的方法，要求信号从时域转换到角域，在角域匹配重构后的信号需要再次转换到时域，因此存在多次转速积分导致的误差，进而使得重构信号在时域上与原信号存在幅值误差。该对比方法与所提方法的信号重构效果如图6所示，从图6(a)和图6(c)可看出，所提方法的时域重构信号幅值更为准确。分别计算2种方法下，重构信号与原信号的均方根误差(RMSE)，得到对比方法的均方根误差为13.92，而所提方法的均方根误差为6.16，仅为对比方法的44.3%。从图6(b)(d)的剩余信号比较也可以说明这一点：按照对比方法提取出分布型故障后的剩余信号中，包含的残余分布型故障信号成分更多，仿真冲击信号在该剩余信号中的信噪比(SNR)为-1.24 dB，而在所提方法中，该值为0.34 dB，信噪比大幅度提高。

图6 分布型故障信号重构效果对比

2.2 有噪声仿真

在原信号中添加信噪比为10 dB的高斯白噪声，此时分布型故障信号和局部型故障信号的信噪比分别为-0.72 dB和-12.56 dB，复合故障信号如图7(a)所示。利用所提方法，求得各轴转速，截取3～4 s的信号和对应转速，构造时域调频字典。迭代阈值设为εp=1，利用匹配追踪重构出的分布型故障信号时域如图8(a)所示，重构信号与原信号的RMSE值为6.33。阶次谱图8(b)中，调制边带特征已全部重构出来，阶次间隔为0.56阶，与表1中设定的输入齿轮特征阶次相合。如图7(b)所示，剩余信号中，冲击故障特征已比较明显。重构信号如图9所示：时域图9(a)中，红色重构信号与原仿真信号的各冲击时刻重合，故障信号特征得以有效提取，阶次谱图9(b)中清晰呈现出故障输入齿轮的调制边带阶次(1阶)。

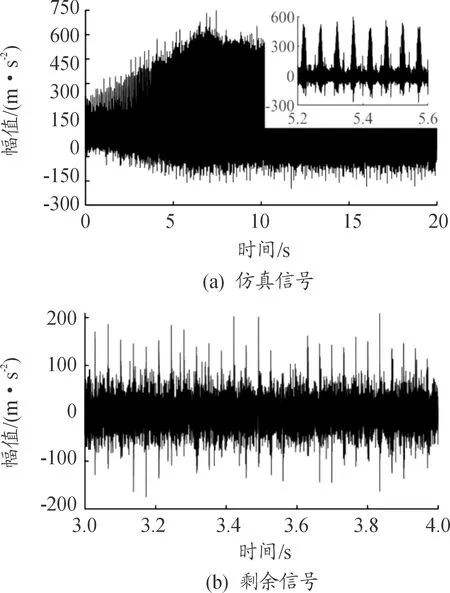
图7 仿真信号与剩余信号

图8 分布型故障重构信号与仿真信号

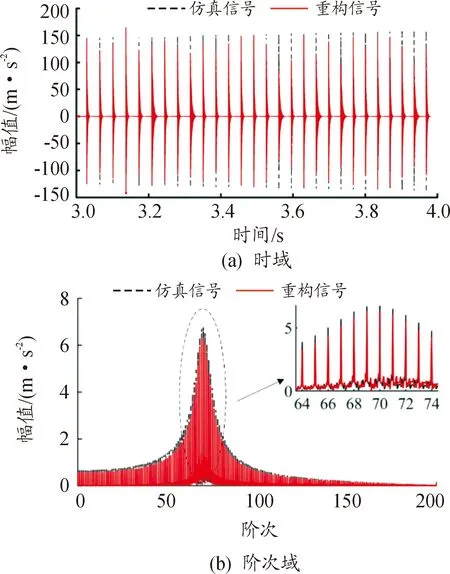
图9 局部型故障重构信号与仿真信号

对比无噪声条件下，所提方法重构的分布型故障信号与原信号的RMSE值(分别为6.33和6.16)，二者的相关系数值为0.995 7，可以看出由于噪声影响，重构信号与原信号相关系数性略有下降，但仍然处于较高水平，证明所提方法在噪声条件下仍具备较好的重构精度，在与对比方法的比较中更能说明这一点。

对比方法与所提方法重构后的分布型故障时域信号如图10所示，可以看出所提方法的重构信号幅值匹配更为准确。计算可得，对比方法中，重构信号与原信号的 RMSE为14.61，而所提方法的RMSE为6.33，仅为对比方法的43.3%。

图10 分布型故障信号重构效果对比

2.3 误诊性验证

由无噪声和加噪的仿真信号验证了所提方法对于复合故障诊断的有效性，可以重构出淹没于分布型故障信号中的相对微弱的冲击信号，避免了局部型故障的漏诊。为了进一步验证所提方法不会造成误诊，从2.2节设置的加噪仿真信号中去除局部型故障信号成分，模拟信号中只存在分布型故障的情况。图11(a)为截取的3～4 s仿真信号时域图，图11(b)为利用所提方法重构出的信号阶次谱图，故障转频调制边带清晰可见。

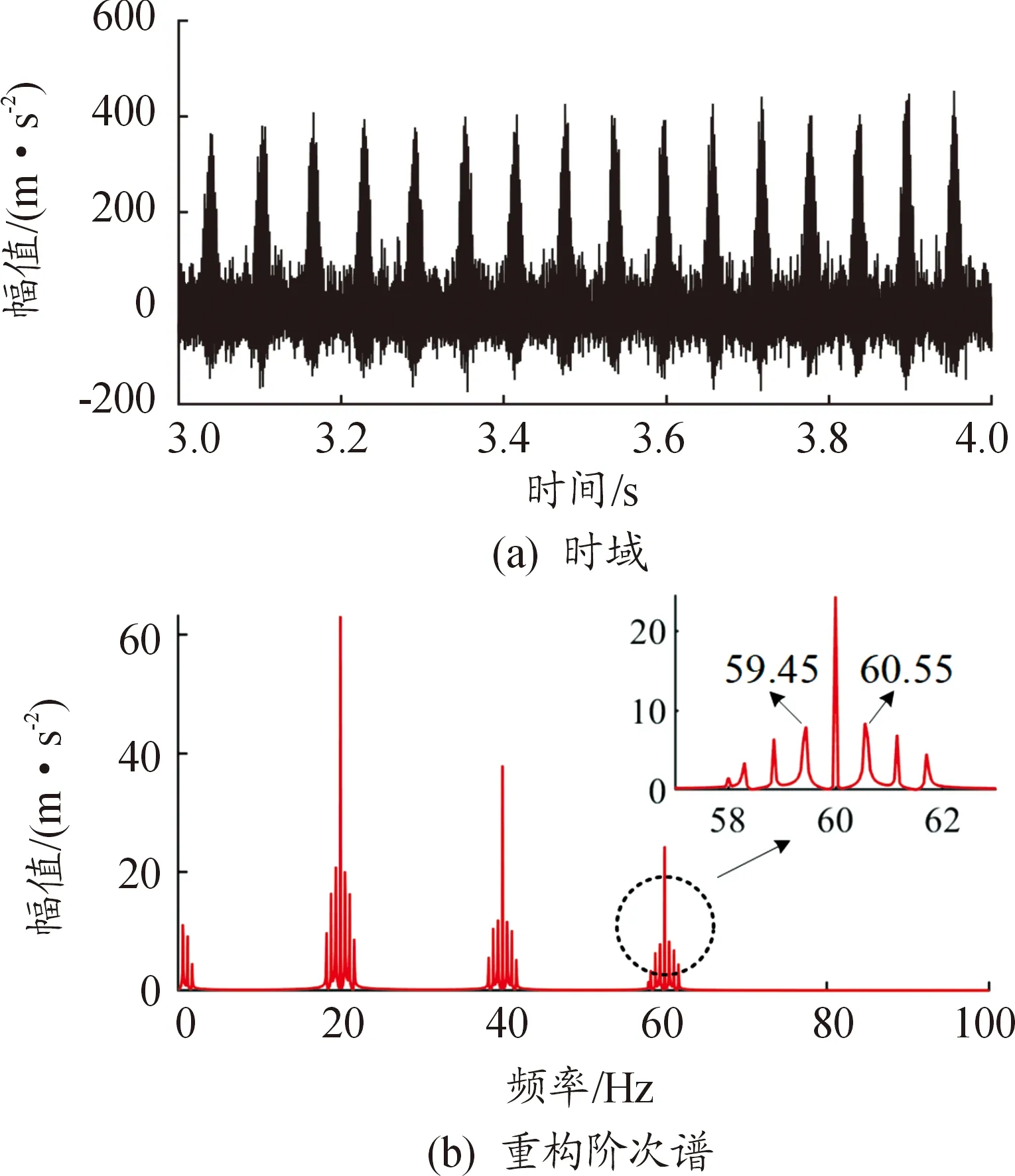
图11 分布型故障仿真信号

如图12所示，剩余信号中无明显冲击序列，对其利用所提方法进行局部型故障信号重构，从图13的重构信号时域和阶次谱中可以看出，重构信号中仅仅包含少量的噪声分量，无冲击调制特征，证明所提方法不会对故障类型进行误判，也不会对不存在的故障造成误诊。

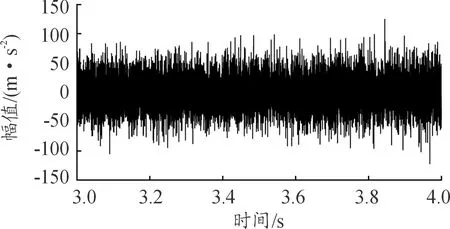
图12 剩余信号

图13 局部型故障重构信号

3 实验分析

被试齿轮箱为某汽车三轴5挡变速器，变速器工作挡位为5挡，在第5挡输出轴齿轮断齿故障进行试验，如图14所示。齿轮箱负载为50 N·m，以输入轴为参考轴，其各级齿轮结构参数及阶次特征参数列于表2。采样频率为12 kHz，采集输出轴轴承座垂直方向的振动加速度信号进行分析。

图14 故障齿轮

表2 测试齿轮结构参数

采集的齿轮箱振动加速度信号x(t)如图15(a)所示，时域图中有效信号均被噪声掩盖，无明显的周期信号成分。频谱图(b)中，由于变转速所导致的频率混叠现象严重，无法从中得出故障齿轮位置及故障类型的相关信息。

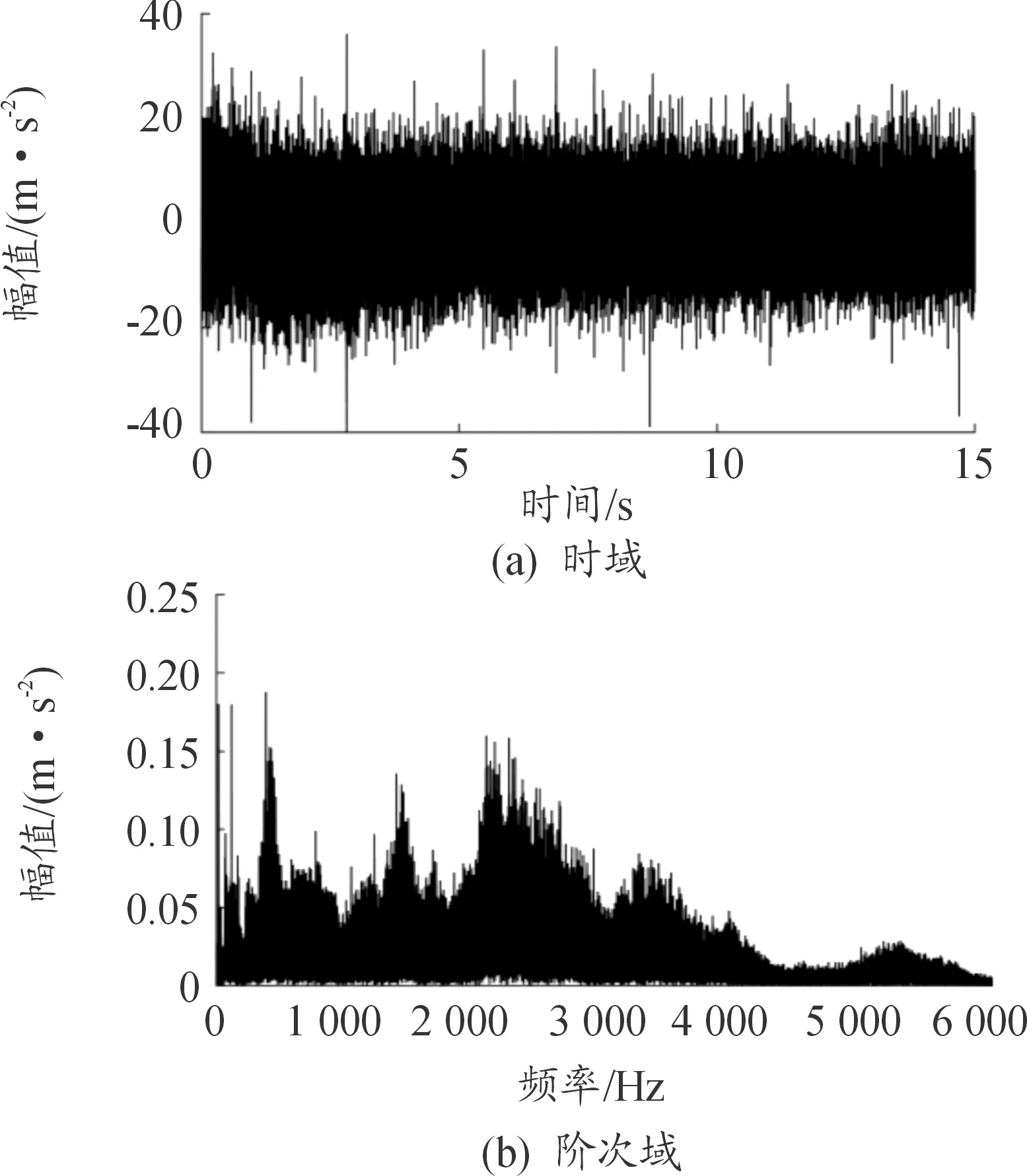
图15 试验信号时域和频域

按1.2.3节所述流程，首先求取输入轴瞬时转速r1(t)如图16所示。

图16 求取转速

由图16可见此时齿轮箱处于降速过程，转速变化较为缓慢。截取第4～5 s信号进行分析，记该段信号为xc(t)，对应的转速记为rc1(t)，则输入轴转频fnc1(t)=rc1(t)/60，利用表2中的齿轮箱各齿数比可求出中间轴转频fnc2(t)和输出轴转频fnc3(t)，啮合频率最高阶次和调制边带最高阶次分别设为K=4，L=5，覆盖阶次为28.7×4+1.3×5=121.3阶，保证避开最高共振阶次(150～200阶区间)，以减少在分布型故障阶次成分提取中，共振阶次成分的影响。相位分段数I取24，按照式(5)构造调频字典，匹配追踪的阈值εs=0.1。

时域重构信号xstd(t)为图17(a)中的红线部分，阶次谱图(b)中，红色重构信号呈现如下特征：

1) 前1，2，4阶输出轴旋转阶次(1.3 阶)；

2) 第5挡啮合齿轮副的前3阶啮合频率阶次(28.7阶)及间隔为输出齿轮旋转阶次(1.3 阶)的调制边带。

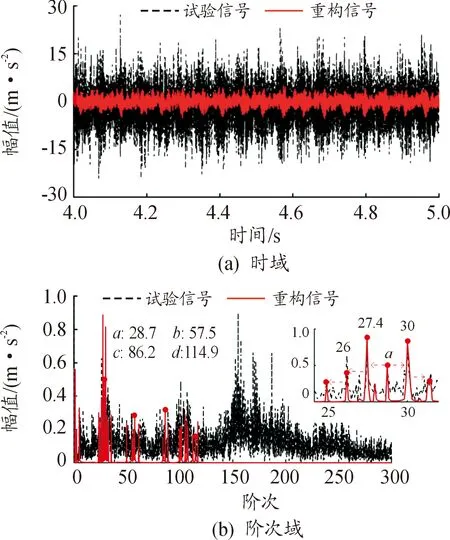
图17 分布型故障重构信号与试验信号

重构结果表明，齿轮箱的输出齿轮或者轴存在分布型故障。此试验中，该故障是由输出轴轴不对中导致的。

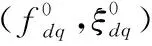
图18 局部型故障重构信号与试验信号

4 结论

1) 构造了具有明确物理意义的稀疏调频字典，融合了齿轮箱特征参数和时变转速，可实现分布型故障信号的有效提取。

2) 采用了基于振动信号的转速估计方法获取字典构造所需的时变转速，无需安装转速计提供转速信息，简化诊断流程。

3) 相比于稳速工况，变速工况下的信号频率特征更为复杂，所提方法既可实现变转速下齿轮复合故障的有效诊断，也可用于诊断稳速工况下的齿轮复合故障。