一种结合清晰区域增强多聚焦图像融合算法

郭锋锋

(宿州职业技术学院 计算机信息系，安徽 宿州 234000)

0 引言

在现实场景中由于光学镜头聚焦特性，形成图像局部清晰图像，如手机拍照当聚焦某一物体时，我们发现物体时清晰但相应其他背景则变得模糊，同理聚焦别的物体时也会发生这种现象。多聚焦图像融合是指提取多幅图中有效信息融合成一幅清晰图像[1]。图像融合技术经过快速的发展，应用场景广泛，应用价值较大，并为后来技术发展做了铺垫[2]。

近年来，图像融合技术发展迅速，先后经过小波、多尺度几何分析函数、神经网络等发展阶段。由于小波[3]不能很好表示图像的奇异性，因而被多尺度几何分析函数[4-6]取代，其中最为典型的基于contourlet变换函数[7]，但是由于contourlet变换不具有平移不变性，且会发生频谱混叠现象，针对contourlet变换缺点将其改进为非下采样contourlet变换(NSCT)，Bhatnagar G等[8]提出了NSCT域的指导对比度多模态医学图像融合，提高图像对比度。闫利等[9]提出了一种NSCT域内结合边缘特征和自适应PCNN的红外与可见光图像融合，通过对边缘特征的有效提取及PCNN对细节信息有效提取，使最终融合图像更加清晰；宋瑞霞等[10]提出了一种NSCT与边缘检测相结合的多聚焦图像融合算法，该算法最终增强融合图像边缘信息；赵春晖等[11]提出了采用WA-WBA与改进INSCT的图像融合算法，该算法通过结合WA-WBA，有效的提取了图像细节信息。

由于NSCT域具有平移不变性且不会发生频谱混叠现象，能更好的分解图像。本文主要思想是通过改进融合规则及通过对原图清晰区域边缘信息提取来对融合后图像进行边缘信息强化，因此本文算法最终融合图像边缘信息突出，图像主观及客观大幅提高。

1 非下采样contourlet 变换(NSCT)原理

由于contourlet 变换的图像不具有平移不变性，而NSCT变换是一种具有局部性，平移不变性，且不存在频谱混叠现象的多尺度几何分析函数，因此NSCT被广泛用于图像融合中。

NSCT是有两组滤波器组成的，即非采样方向滤波器(NSPFB)和非采样塔形滤波器(NSDFB)，如下图1所示，原图首先经过NSPFB滤波，然后在经NSDFB滤波。

图1 本文算法分解原理图

2 本文融合算法原理

算法流程如图2所示：

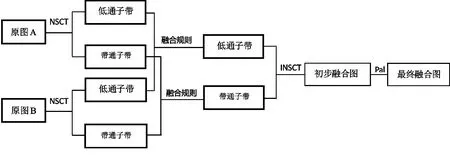
图2 本文算法流程图

(2)提出了改进的梯度能量的规则用于低频子带融合和基于切比雪夫矩的融合规则，并分别用到低通、带通子带融合。

(3)最后采用pal算法对初步融合图像处理，以增强边缘信息，得到融合图像。

2.1基于改进的梯度能量的低频子带融合规则

(1)

其中

fx(i，j)=f(i，j)-f(i-1，j)

(2)

fy(i，j)=f(i，j)-f(i-1，j)

(3)

由公式(1)所示，图像的梯度能量对方向表征不足，因此本文将其改进如下：

(4)

其中fxy、f-xy为归一化的对角像素差，公式如下

(5)

(6)

(7)

2.2基于切比雪夫矩的带通子带融合规则

由于切比雪夫矩的计算中没有近似误差[13]。因此被广泛使用，切比雪夫多项式定义如下：

(8)

正则化

(9)

(10)

其中δmn为克罗内克函数。对于I×J图像f(i，j)的图像切比雪夫矩定义如下

(11)

其反变换为

(12)

由于图像清晰区域对应切比雪夫矩值较大，而模糊区域的值较小。基于此，对于带通子带本文提出如下融合规则：

(1)对原图像A，B分块，块状大小8×8，利用公式(12)，我们可以将图像映射切比雪夫基上，并取该块状中系数最大值作为该块的特征值Tijmax，使各子块有唯一特征值。

(2)用步骤(1)中的切比雪夫矩值Tijmax代表各个表征值，提出如下公式：

(13)

其中TH为极限参数，平滑清晰区域与模糊区域边缘信息。

2.3改进的Pal算法的融合图像边缘增强

李正等[14]提出了一种基于梯度方向一致性的边缘检测算法，该算法较传统算子性能大大提高，但是忽略图像的清晰度。基于此，Pal和King提出了一种基于模糊边缘检测的算法[15]，算法首先将一个I×J的大小图像f(i，j)表示为一个灰度集

(14)

公式中μij/xij为图像中某点(i，j)相对某个特定灰度集Xk的隶属度，其中隶属函数为

(15)

其中Xmax为Xk的最大灰度级；FdFε分别为倒数型及指数型模糊因子。通过增强算子(16)对图像增强。

(16)

式中：

(17)

由于变换后的图像仍然存在轻微的模糊现象，因此本文采用Pal算法进行处理，本文阈值取0.2[15]。将原图A，B经过上述Pal算法处理后得到UA(i，j)和UB(i，j)，再通过UA(i，j)和UB(i，j)对初步融合图像进行清晰区域边缘加强，公式如下

(18)

其中F是最终图像。

3 实验分析

3.1改进的Pal模糊边缘检测实验

如图3所示，在本文选取的几种对比算法针对模糊图像的边缘提取时，不能有效的描述图像聚焦区域边缘信息，只能描述全图的边缘信息，而本文Pal算法[16]能很好的提取图像清晰区域的边缘信息，从上图看出清晰区域提取的边缘信息丰富，而模糊区域几乎不会被提取，能够很好完成本文算法对图像融合信息的加强。

图3 几种边缘检测算法效果比较

3.2图像融合实验

本文选取离散小波(DWT)；平移不变离散小波(SIDWT)；NSCT域的加权平均融合规则(NSCT1)，作为对比算法。图4及图5(a)-(e)分别为罐子桌子图及时钟人物图的五种算法的融合结果图。

图4 罐子桌子图的融合图

图5 时钟图的融合图

从图4和图5融合结果对比，DWT与SIDWT算法对比NSCT算法，前者存在明显模糊现象；NSCT算法明显改善，但是边缘信息不够突出；本文算法由于在融合过程中有效保留边缘信息，并且最后对边缘信息进行了增强，因此主观视觉效果最好。

如表1、表2所示，统计了罐子桌子图及时钟图的图像融合客观指标值，选取能量信息、平均梯度、空间频率和边缘保持度四个评价指标，以上四个指标值越大图像融合效果越好，值越小证明融合效果越差。

表1 罐子桌子图客观评价表

表2 时钟图客观评价表

从客观评价表横向对比，可以得到，四种客观评价指标值，本文算法最优，其他几种算法的值较小。由于图像最后经过清晰区域增强，因此突出了边缘信息，图像变的更加清晰。

客观指标的评价值与主观感觉一致，证明本文算法的优越性。

4 结论

本文通过对融合规则研究，将梯度能量改进，并提出了基于改进的梯度能量自适应融合规则用于低频子带的图像融合；通过对切比雪夫矩的研究，提出了基于切比雪夫矩的带通子带融合规则；最后在对原图像采用Pal算法对原图进行清晰区域边缘提取，用于增强融合后的图像边缘信息，实验结果表明，本文提出NSCT域结合边缘检测算法最终的主观视觉良好和客观评价指标大幅提高，但是存在耗时严重，将在今后的研究中完善。