连续突变管道流动局部水头损失建模研究
2021-10-19方斌
方 斌
(上海飞机设计研究院,上海 201210)
0 引言
管道设计在动力燃油系统、水利设施、农业以及工业管道中应用十分广泛,在工程应用中管道系统通常比较复杂,流体在复杂管道中流动存在不同程度的流动损失,包括沿程阻力损失和突变管道部位的局部阻力损失等,其中突变管道部位的局部阻力损失最为严重,而流体的水头损失一直是管道工程设计人员所关注的问题,因此对突变管道部位的局部阻力损失的研究具有重要的实际意义[1]。
由于突变管道流动水头损失对管道系统设计具有重要影响,目前已经有大量针对突变管道流动特性的研究。门宝辉[2]通过实验研究了突扩管道的局部阻力系数随管径比的变化情况,并用理论推导的方法表明突扩管道的局部阻力系数不仅与管径比有关,还与流体速度有关,但未指明局部阻力系数与流体速度的具体关系。张俊婷和许自顺等人[3-4]通过数值计算的方法对突扩、突缩以及渐变管道的局部阻力损失系数进行了研究,其研究结果表明突扩管道的局部水头损失系数随着雷诺数的增大而增大,随管径比值的增大而减小;但其研究结论同样未指出局部水头损失系数与雷诺数和管径比之间的具体变化关系,同时其数值计算结果并未设计实验验证,计算结果的准确性有待研究。王战辉等人[5]通过数值模拟的方法研究了突扩管道在不同管径比和进口流速下流场中压力和速度分布情况,研究结果表明,在截面突变处流动出现死区,并且突扩截面前后压差随管径比和进口速度的增大而增大。张华[6]通过理论分析得到了突变管路截面速度分布与局部阻力系数之间的关系,计算准确性较好。李栋浩等人[7]设计实验研究了雷诺数及收缩比对局部阻力系数的影响,实验数据表明在不同收缩比情况下,局部阻力系数与雷诺数的对数值成明显的线性关系。
通过总结前人对突变管路流动特性的研究可以发现,目前针对于管径比以及流体进口速度对突变管道流动水头损失影响的研究较多,并且多集中在定性研究,对建立经验模型的研究较少;此外,目前对于突变管道的研究基本都是针对单个的突扩突缩管道,对于连续的突变管道的流动研究较少。
鉴于此,本文将对连续的突扩突缩管道的流动特性展开研究,流体为RP-3航空煤油,分别研究四种不同管径比的连续突变管道在不同进口速度下的流动特性,并总结得到连续突变管道流动水头损失的经验模型。
1 突变管道局部水头损失理论分析
1.1 管道模型
在实际工程应用中,管道系统上通常设置有较多限流装置,如阀门、限流孔等,这种带限流装置管道的基本特征是突变前后的管径相同,并且突变部分的长度较短;因此,本文将以这种典型的管道结构为对象展开研究,这种典型带限流装置管道的剖面结构如图1所示。
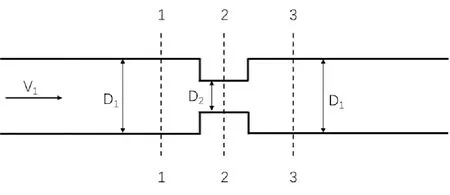
图1 限流管道剖面示意图
流体先以入口速度V1进入到突缩段,随后立即进入到突扩段,其中突缩前部分1-1截面和突扩后部分3-3截面的管相同,均为D1,缩小部分2-2截面的管径为D2。流体在短距离管道中连续经过突缩和突扩两级突变,流动状态为复杂的湍流,流体经过突变管道后存在不可恢复的压力损失,并且进口雷诺数越大,不可恢复的压力损失也越大[8]。
由于管道中的限流装置长度较短,可以忽略其中的沿程阻力损失,水头损失主要由突变截面的局部损失造成。
1.2 传统计算方法
目前对于单个突扩或者突缩管道流动局部水头损失的研究较多,根据传统计算方法,突变管道的水头损失计算方法为[9]:

(1)
其中,v进为单个突变管道的进口处流体速度,ξ为突变管道的局部损失系数,对于单个突扩管道和单个突缩管道,其局部损失系数分别为[10]:

(2)
其中,ξ扩和ξ缩分别为单个突扩和突缩管道局部损失系数,A前和A后分别为突变截面前后的管道流通面积。
对于如图1所示的连续突缩和突扩管道流动水头损失,可利用传统方法进行叠加计算,具体计算方法为:
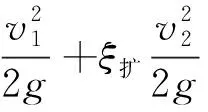
(3)
其中,v2为缩小管道部分2-2截面处的平均速度。
由流量连续得到:
A1v1=A2v2
(4)
并且:

(5)
将管径比表示为:

(6)
因此,图1所示的连续突缩和突扩管道流动水头损失的传统理论计算方法可进一步表达为:

(7)
1.3 理论分析
对于连续突缩突扩管道整体的流动能量损失分析,首先针对图1中的1-1截面到3-3截面建立能量方程:

(8)
其中,z1为1-1截面相对于基准面的垂直高度;p1为流体在1-1截面处的静压;ρ1为流体在1-1截面处流体的密度;z3为3-3截面相对于基准面的垂直高度;p3为流体在3-3截面处的静压;v3为3-3截面处流体的平均速度;ρ3为流体在3-3截面处流体的密度;ht2为流体从1-1截面到3-3截面之间的流动水头损失。当管道水平放置时:
z1=z3
(9)
对于1-1截面到3-3截面,由流量连续得到:
A1v1=A3v3
(10)
对于不可压缩流动,流体密度不变,因此:
ρ1=ρ3
(11)
在后续的推导和计算中,流体密度统一用ρ表示。
将式(9)~式(11)代入到式(8)中得到流体从截面1-1到截面3-3的流动损失为:
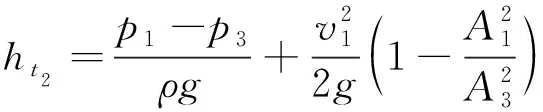
(12)
根据式(12)分析可以发现,连续突变管道中的流动局部水头损失由三部分决定,分别是突变管道前后流体的静压差、流体的入口速度以及突变前后管道的流通面积之比。
对于本文中分析的典型的带限流装置的突变管道,由于突变前后的管道流通面一致,流体从截面1-1到截面3-3的流动损失为:

(13)
从式(13)可以发现,典型带限流装置的突变管道流动的局部水头损失由突变管道前后的静压差决定。对于单个突变管道局部水头损失,传统计算方法中使用动量方程将压差近似转化为速度及管道尺寸参数,由此叠加计算得到连续突缩突扩管道水头损失必然存在误差;此外,由于在连续突缩突扩管道中,流体经过第一个突变后会产生旋涡,流体流动状态为复杂的湍流流动[11-12],由于两个突变截面间的距离较短,在第二个突变截面入口处流体速度分布极不均匀[13],此时由传统方法计算得到的流动水头损失误差进一步扩大。
对于典型带限流装置的突变管道流动水头损失分析,由于管道长度较短,管道沿程阻力损失可以忽略,水头损失主要由突变截面的局部水头损失造成。因此,为了研究连续突变管道水头损失,就必须确定突变截面前后压差的影响因素及其影响规律,突变截面前后压差的影响因素可能包括流动参数、管道结构参数等,接下来将通过实验进行研究。
2 实验设计
2.1 实验管道
为了研究典型带限流装置的突变管道流动水头损失,设计了如图2所示的实验管道。实验管道设计有四组不同管径比;在距离管道突缩截面上游500 mm处设置有压力表,在距离管道突扩截面下游500 mm处和600 mm处分别设置有压力表和质量流量计,并可由流量值计算得到相应位置处的流体速度;测量装置距离突变截面超过6倍管径D2,在距离突变截面6倍管径位置处流动旋涡基本消失,因此可以避免流动旋涡对测量装置精度的影响[1]。

图2 实验管道示意图
2.2 实验工况
实验在常温常压条件下进行,管径比β有四种,每种管径比又设计有23种不同流量,具体如表1所示。

表1 实验工况表
为了实验结果的准确性,每次实验都等到流量计数值稳定以后才开始记录数据,并且每个工况点都在稳定后持续30 s,然后在30 s内共记录5组数据,最后取这5组数据的平均值作为该工况下的实验值。
3 实验数据分析及模型修正
3.1 数据分析
首先分析管道进口处航空煤油的雷诺数对连续突缩突扩管道的局部水头损失的影响。根据流量计的测量数据可计算得到管道的进口速度v1,进一步根据管道尺寸可以获得管道进口处航空煤油的雷诺数,根据雷诺数的计算方法:

(14)
其中,ρ和μ分别为航空煤油的密度和动力黏度,本实验在常温下进行,此时取密度为780 kg/m3,动力黏度为1 038μPa·S[14];v为管道的进口速度v1;L为管道进口部分的特征长度,即进口部分的管径D1。四种管径比的理论和实验水头损失随进口雷诺数的变化如图3所示。
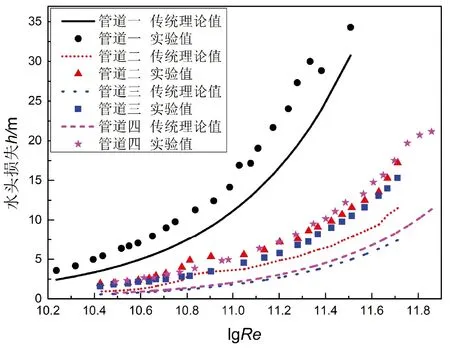
图3 连续突变管道水头损失随雷诺数变化
由图3可以看出,连续突缩突扩管道流动局部水头损失随管道进口雷诺数的增大而增大,但并未随管径比的变化而呈现出明显的递变规律;由传统的突变管路局部损失叠加计算法得到的水头损失理论比实验值偏小。由以下方法分析四种不同管径比的连续突变管道在23种不同进口流量下的水头损失,根据式(15)计算传统方法理论值相较于实验值的平均偏差,得到表2的数据。

(15)

表2 传统理论局部水头损失计算误差
由表2中的数据可以发现,管径比越大,理论计算值与实验值的偏差越小,即管径比越大,传统的局部损失叠加计算法误差越小。
3.2 模型修正
对实验数据进一步分析发现,四种不同管径比的突变管道局部水头损失实验值、理论计算值及管径比与进口雷诺数存在较为明显的变化关系,即:

(16)
采用多项式拟合的方法进行分析,发现四种不同管径比的突变管道局部水头损失随进口雷诺数的变化基本呈线性函数关系,具体为:

(17)
其中R2表示的是多项式拟合的方差,方差越接近1则拟合准确度越高;反之,则偏差越大。从多项式拟合结果分析发现,一号管道的偏差相对较大,二、三及四号管道误差相对较小。因此,可以总结得到突变管道局部水头损失实验值、理论计算值及管径比随进口雷诺数变化的一般形式为:
f=a·lgRe+b
(18)
其中,a和b为线性函数的两个待定系数,从拟合得到的函数关系发现四种不同管径比的管道的待定系数a和b变化较大,初步分析认为两个待定系数与管道的管径比相关,再次利用多项式拟合的方法分析待定系数a和b与管径比的关系,得到:
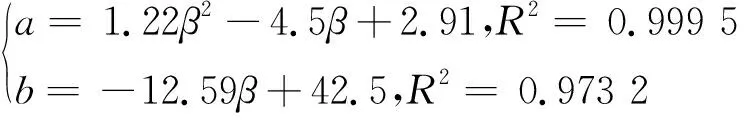
(19)
因此,综合以上可以得到:
即:
由此可以得到修正的连续突缩突扩管道局部水头损失计算模型为:
其中修正因子为:
为了验证修正模型的准确性,利用修正模型计算连续突变管道局部水头损失,并与实验值及传统经验模型计算值进行对比验证,四种管道的对比结果分别如图4~图7所示。

图4 管道一模型计算结果对比
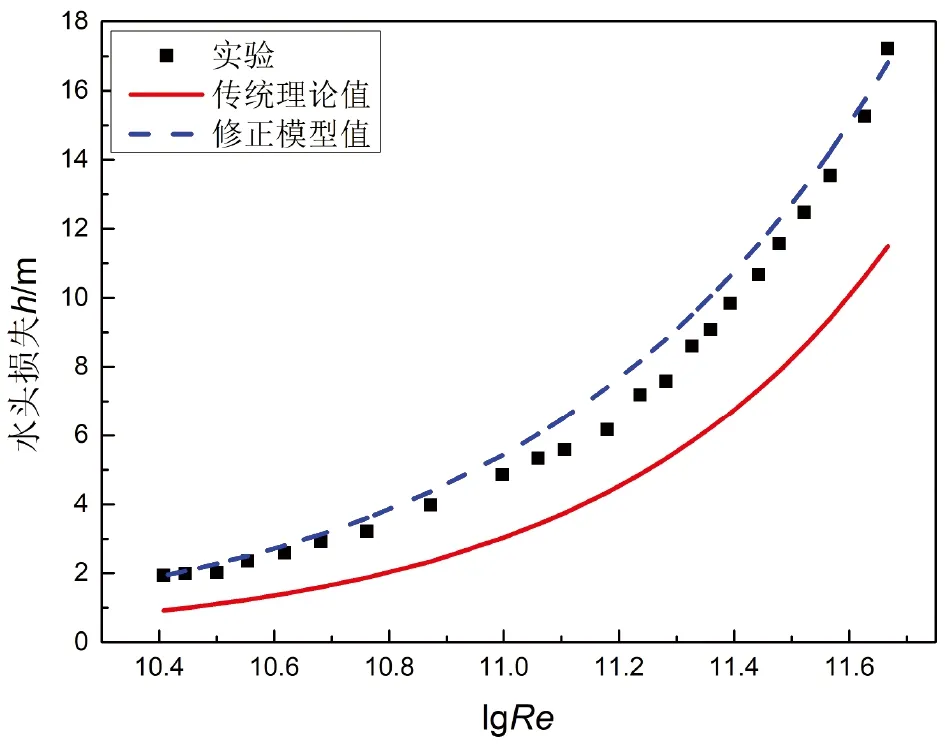
图5 管道二模型计算结果对比
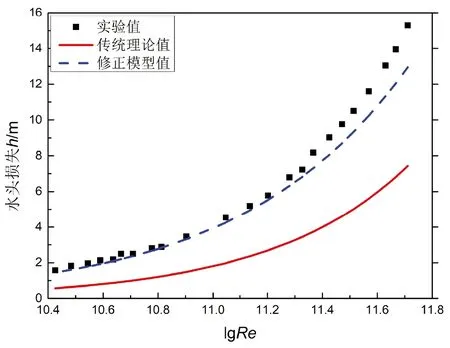
图6 管道三模型计算结果对比
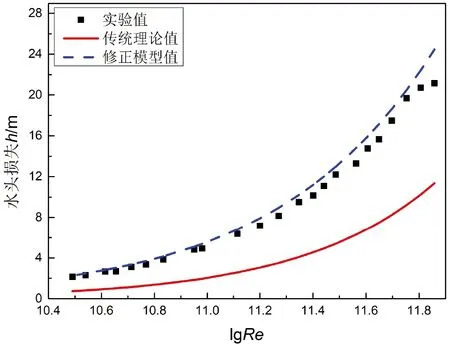
图7 管道四模型计算结果对比
分析图4~图7可以发现,对于连续突缩突扩管道的局部水头损失计算,修正模型的计算结果相比于传统理论的叠加计算法精度有显著的提高,修正模型与传统理论的连续突缩突扩管道的局部水头损失计算误差对比结果如表3所示。

表3 修正模型局部水头损失计算误差对比
从表3可以看出,修正模型的计算结果误差均在10%以内,但修正模型计算相比于实验值均略微偏大。总之,修正模型相比于传统方法能更准确的描述连续突缩突扩管道的局部水头损失。
4 结论
本文对典型连续突变管道局部水头损失的研究结果表明:
(1)连续突缩突扩管道局部水头损失随进口雷诺数的增大而增大;
(2)对于连续的突变管道的局部水头损失计算,基于传统理论的突变管道局部水头损失叠加计算法误差较大,且计算结果比实际值偏小,可能的原因是传统理论的突变管道局部水头损失计算法未考虑短距离突变时湍流涡的能量损失;
(3)基于传统理论的突变管道局部水头损失叠加计算法的计算误差随管径比的增大而减少;
(4)本文结合实验数据分析及传统理论的突变管道局部水头损失叠加计算法,推导得到了连续突缩突扩管道局部水头损失计算的修正模型,该修正模型有效提高了计算精度,修正模型计算结果与实验数据对比表明修正模型误差低于10%,为典型的连续突缩突扩管道的局部水头损失计算提供了有效方法。
