基于核心素养的小学数学量感习题编制的探索

摘 要 在小学阶段，“量感”主要是指学生对长度、面积、体积、时间、质量、货币等的感性认识。因而，关注小学生数学量感的形成和习题编制有助于促进学生空间观念的培养，发展学生思维能力，提升问题解决能力。编制习题是可以从简单图形入手，借助估测活动，渗透思想方法，化抽象为具体，从而了解学生的量感学习水平和存在问题，帮助教师进行总结与反思，以便调整和改进教学内容与教学过程。

关键词 小学数学 核心素养 量感 习题编制 探索

“数”与“量”是不可分割的。顾名思义，“数感”是“数”的感觉，“量感”就是“量”的感受。“量感”与“数感”一样，都有一定的抽象性，同是思维的产物，都与生活有着密切的联系。量感专指对物体的大小、多少、轻重、松紧、快慢、厚薄、粗细等量态的感觉。在小学阶段，量感主要是指对长度、面积、体积、时间、质量、货币等的感性认识。因而，关注小学生数学量感的形成和习题编制有助于促进学生空间观念的培养，发展学生思维能力，提升问题解决能力。笔者下面结合自己多年来的教学实践，谈谈如何编制习题以了解学生量感学习水平、进行教学反思、调整和改进教学的体会。

一、从简单图形入手，理解量感本质

生活是数学的源泉。“万物皆可数”，万物皆可量，量感离不开对生活实际的直观理解。编制小学生数学量感习题离不开学生周遭熟悉的、有趣的事物。要编制有关长度、面积、体积、容积、质量等概念的习题，离不开对长度单位、面积单位、体积单位、容积单位、质量单位及其计算和换算的理解。

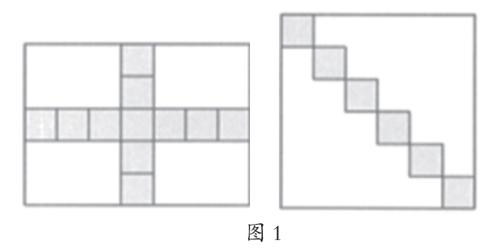
如在编制人教版《数学》三年级下册“面积”一课练习时，因为第一学段学生所感知的生活面有限，于是我们选择了与长度测量有直接联系的活动，设计了这样一道题目：图中每个小方格表示1平方厘米，请说说长方形和大正方形的周长和面积各是多少？

众所周知，图形与数量联系着测量。量感是一种对“量”的直觉和敏感性，是对“量”的直接反映。比较是量感的基础，量感意味着与参照标准的比较。题目虽然没有直接给出长方形的长与宽和正方形的边长的具体数据，表面看计算它们的周长和面积似乎无从下手。然而，只要有了边长为1厘米的小正方形作参照标准，学生就可以通过观察、比较，经历“拼一拼”的思维活动，直观地感悟出长方形内横向摆的小正方形的个数是7，即为长方形的长为7厘米;纵向摆的小正方形的个数是5，即为长方形的宽为5 厘米;同理，大正方形的边长为6厘米。然后，根据计算公式得出，长方形的周长为（7+5）×2=24（厘米），面积为7×5=35（平方厘米）;大正方形的周长为6×4=24（厘米），面积为6×6=36（平方厘米）。显然，我们还可以让学生动手“画一画”，补画成格子图，再纵横双向数一数，长与宽的信息便跃然纸上，周长和面积问题即可迎刃而解。题中带导，导中带思，一边循序渐进启发和培养学生的几何量感，一边以形代量，以量解形，考查学生利用量感获取信息解决问题能力。

二、巧借估测活动，比较量感体验

测量的本质就是与标准尺度进行比较。而估测是用标准计量单位对具体实物作出量化判断的过程。要测查学生的估测能力，首先要测查学生是否亲历测量的全过程。考查其在估测过程中采用的估测方法是否科学合理，符合逻辑;测查学生所估测的结果与实际情况是否接近，误差值有多大？并对估测结果的合理性作出中肯的评价。

生活中我们经常会遇到许多不规则的图形，如脚印、湖面等，结合人教版《数学》五年级上册第六单元“多边形的面积”的巩固练习，格子图是编制无规则图形面积练习题不可或缺的工具，面积的度量离不开面积的不变性和可加性，数方格法、重叠法、割补法等均可用。

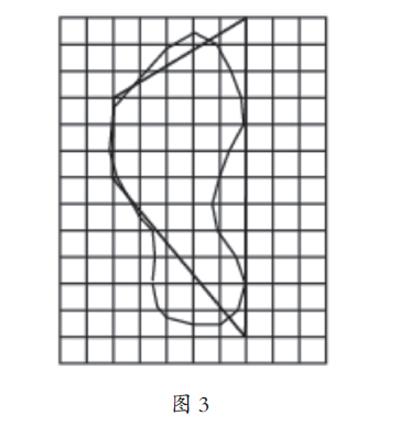
例如请你估测出下图脚印的面积大约是（    ），并写出你的思考过程（每个小方格的边长是1厘米）。

显然，借助方格图数格子是估量不规则图形面积的常用方法之一。本题可以通过数方格图，满格的算1格，不满格算半格，很快得出脚印的面积是37.5平方厘米。其次，可直观地将脚印看成是上底3厘米、下底12厘米和高5厘米的近似梯形，再根据梯形的面积公式进行计算，也是可行的（如图3）。（3+12）×5÷2=37.5（平方厘米），即图中脚印的面积大约是37.5平方厘米。

举一反三，我们还可以将组合图形分割或填补成若干个规则图形，之后再对规则图形进行拼算和估算，格子分得越细，估测结果的误差就越小。鉴于此，本题可能出现多种解法、多种答案也在情理之中。通过估测脚印面积的活动，可以考查学生对三角形、长方形、正方形、梯形面积的认识及计算公式应用能力。

三、渗透思想方法，促进量感内化

小學生数学量感的形成是一个由抽象到具体的过程，而数形结合思想、极限思想和度量思想等，就像在具象与抽象之间架起一座桥梁，将量感培养与数感的形成进行有机“嫁接”，从而给学生更为直观的量感体验。量感的培养并不是在“单一量”的感受、体验之中形成的，更是在量与量的比较中得到不断深化发展。

如编制人教版《数学》六年级下册第三单元“圆柱和圆锥”练习时，测量铁球体积的实验过程：先将300mL的水倒进一个容量为500mL的杯子中，再将4颗相同的铁球放入水中，结果水没有满;再将一颗同样的铁球放入水中，结果水满溢出，根据以上过程，请推测这样一颗铁球的体积大约在（   ）cm3以上，（   ）cm3以下。

本题的设计意图，是通过图4-2、图4-3两个杯子的水位比较，利用水位差，进行体积与容积之间的转化，直观地得出1个小球的体积。让学生经历量与量的比较、转化，形成对一些微小数量和一些宏大数量的认知，拓展了学生对量的认知，进一步丰实了学生的量感，拓宽了学生量的内化领域，奠定了学生量感可持续性发展的基础。与小球数量变化直接相关的不是300mL的注入水，也不是容量为500mL的杯子，而是注水后所剩的200mL容积。200÷4=50（cm3），放入4颗小球水面没有到达500mL刻度线，说明每个小球的体积小于50cm3;同理200÷5=40（cm3），如果放入5颗小球时水面刚好到500mL刻度线，说明每个小球的体积等于40cm3。一旦出现水满溢出的现象，便可推断每个小球的体积大于40cm3。

四、突破抽象迷思，拓深量感内涵

实践告诉我们，生活中常见的量有两种：一种是直观的“量”，而另一种是比较抽象的量。直观的量可以通过某种表现或者事物体现出来，如长度单位。而抽象的量，需要通过特定的检测仪器才能测定，或是让学生自己亲历知识形成过程，经过一番推理，方能获得感悟。如时间单位、质量单位等。练习题的编制要让学生以数学的眼光，从现实生活中发现问题和提出问题，并探索出解决问题的有效方法和策略，能完整地表达解决问题的全过程，尝试解释探索得到的结果。题目有难有易，难度是指练习题的难易程度，主要根据考查的目的来选定。如果一道习题的难度值为1，即全班都答对。这道题对鉴别学生的实际水平就无多大意义。反过来，如果难度值为0，大部分学生不得分，那么，这道题对于鉴别考生的实际水平也没有意义。所以，习题编制的难度值一般控制在0.8至0.9为宜。而选拔人才和竞赛的试题应另当别论，一般应控制在0.5左右。

在编制人数版《数学》二年级下册第八单元练习题时，我们让大家选择：

估计一下，3号杯中的水大约重（    ）。

A.40克 B.30克 C.60克 D.100克

从题中看出，1号图测的是1个空杯的重量，2号图测的是1个空杯和半杯水的重量，3号图是一整杯水的重量。由此可知，1个空杯重20克，空杯加半杯水的重50克，量感是直观的。那么，通过计算得出，半杯水的重量为：50﹣20=30（克），通过推理得出：1杯水的重量是：30×2=60（克），故选C。本题的解答关键是求出半杯水的重量。因此，解答这类习题时，一定要注意观察，展开推理，即3号图杯中的水的重量不能由2号图的重量直接乘2获得，也不能由2号×2-1号=80（克），应由表及里，化抽象为直观，化未知為已知，化难为易，化繁为简，先求出半杯水的重量。具体事物具体分析，一步一步地向问题深处思索，否则就会陷入迷阵。

总之，小学数学增强和培养学生的量感意识，对促进学生学习计量单位，提高估测能力，拓展数学思维，提高教学水平意义深远。学生的量感培养不应成为数学教学的一个盲点，需要引起教师的重视。在编制有关的量感习题时，应立足于生活实际，遵循学生的身心和智力发展特点，控制好难度值，贯穿于量感形成的全过程，让学生通过身边熟悉的生活素材亲自去体验，发展多维感知，自己动手操作，进行合情推理，逐步形成较强的量感。

参考文献

[1] 中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012：2-3.

[2] 史宁中.推进基于学科核心素养的教学改革[J].中小学管理，2016（02）：19-21.

[3] 谢清霖，郑璘玲.指向核心素养的小学数学评价命题探索——以莆田市小学四年级上册教学质量监测内容为例[J].新教师，2018（06）：46-47.

[4] 谢清霖，郑璘玲.指向学生数学推理能力评价的试题命制[J].教学与管理，2021（14）：66-68.

[责任编辑：陈国庆]