基于流激响应伪信号处理的拱坝运行模态识别方法

宋蕾 刘中明 盛明强

摘要：针对高拱坝流激响应信号中内蕴噪声易造成泄流结构运行模态识别失真的问题，提出了一种基于流激响应伪信号处理的高拱坝运行模态识别方法。考虑到高拱坝泄流振动实测响应信号易被噪声掩盖等特点造成的真实信号难以提取问题，在分析高拱坝结构模态混淆产生机理的基础上，对其响应序列中可能导致结构模态失真的带宽信号掺入人工伪信号，以提升其信号序列的频部显著性。据此，提出了自适应噪声完备集合经验模态分解的密频结构振动响应信号分解方法，进而运用希尔伯特-黄变换方法与随机减量技术对其运行模态加以识别。工程实例表明：所提方法能够有效抑制高拱坝结构参数识别中的模态混淆现象，同时还可避免模态信息丢失，提高参数识别精度。

关 键 词：高拱坝;流激振动;模态混淆;伪信号处理;参数识别

中图法分类号：TV122

文献标志码：A

文章编号：1001-4179（2021）09-0178-08

DOI：10.16232/j.cnki.1001-4179.2021.09.029

0 引 言

隨着锦屏一级、小湾、溪洛渡等具有高泄洪功率、大泄流量的特高拱坝的运行，高拱坝的运行与安全管理难度已远远超出了当前的认知，依托监测资料有效开展大坝结构运行安全性态判诊和损伤识别是坝工领域研究的前沿问题。泄洪水流诱发的坝身结构振动问题是坝工领域研究的难点与重点，获取合理的泄流结构的模态参数是有效判诊结构运行健康状态的重要技术手段之一[1-2]。高拱坝由于难以实施有效的人工激励及难以确定水流荷载等原因，从工作环境泄流激励下结构振动响应的角度，利用实测坝体泄流振动响应信号进行结构模态参数识别在近年来已成为研究的热点问题之一[3-4]。

环境激励下坝体结构模态识别的方法主要有频域分解法[5]、随机子空间法（Stochastic Subspace Identification，SSI）[6]、随机减量法（Random Decrement Technique，RDT）[7]、希尔伯特-黄变换（Hilbert-Huang Transform，HHT）[8]等。李火坤等[9]将频域分解法应用于高拱坝洪水激励运行模态参数识别，验证了只采用坝体泄流时结构所产生的振动响应信号进行模态参数识别的可行性。田鹏明等[10]采用RDT方法对悬臂梁进行模态识别，但随机减量方法在处理非平稳信号时显得无能为力。HHT是由黄锷等[11]提出的一种非线性数据自适应分析方法，先由经验模态分解（Empirical Mode Decomposition，EMD）提取原信号的本征模态函数（Intrinsic Mode Function，IMF），再利用Hilbert变换识别结构模态信息。想要精确辨识出结构模态参数，对被识别信号有较高的质量要求，但在工程实际中，泄流激励下高拱坝振动响应信号大多表现出非平稳、非线性特征[12-13]。经验模态分解的优点在于能较好地自适应对非平稳信号进行分解，而EMD分解过程中的一个重要局限就是模态混淆问题。Huang[11]在对含间歇信号的分解研究中提出通过预先规定极点间距的最大值实现间断判别从而抑制模态混淆的思想。将间断事件视作高频信号，使振动响应信号经小波[14]等方法分解组合后再进行EMD分解是信号滤波法的解决路径，但在滤波后仍会有异常信号及噪声残留，滤除效果不佳。辅助信号加入法[15]是通过在原始信号中添加一定频率幅值的辅助信号，使重构后的新信号分布趋于均匀化，收拢异常端点值，实现抑制模态混淆的效果。María E.Torres等[16]提出了自适应噪声完备集合经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN），其本质是基于EMD的发展和改进，能够有效抑制间歇信号对分解影响的同时较好地消除辅助残余噪声。

振动信号分解是结构模态参数识别的基础，且不同本征模态函数质量会干扰后续模态参数识别的精度，而发生模态混淆则会极大程度上影响分解质量[17-18]。由于考虑到大坝结构的刚度和质量是变化的且实测资料易受噪声干扰，导致所测信号时常包含间断事件及密集模态两个方面。为此，本文针对高拱坝泄流振动信号分解中的模态混淆现象，综合考虑两方面因素作用，提出了伪信号处理技术联合CEEMDAN分解的信号分解方法，并将该方法应用于HHT-RDT模态参数识别中。本文分别通过仿真信号与某实测高拱坝结构原型振动响应数据，验证了其在模态识别过程中的有效性。本文所提方法在避免模态信息丢失的同时，可提高模态参数识别精度，具有一定的工程实用价值。

1 高拱坝振动信号分解的模态混淆处理

任一复杂的信号均可分解为多个本征模态函数之和，将EMD分解用于原始信号后可得到i阶IMF分量yi（t）和一个残余分量r（t），其中各阶IMF应是单一频率的，然而当原始信号序列中存在信号间断或有2个及以上模态频率相近时，如直接对原始信号进行EMD分解则会导致前几阶IMF发生混淆[19]，不能准确获取被测结构真实的各阶模态参数。根据模态混淆的成因，具体可分为模态混与模态叠两种：模态混多因原始信号存在间断事件导致，经EMD分解后恒定模态的部分和瞬态模态被分解于同一IMF中;模态叠则因被测工程为密频结构，多个频率相近的模态经EMD分解后处于同一IMF中，或单阶模态被分解于多个IMF中的现象[20]。

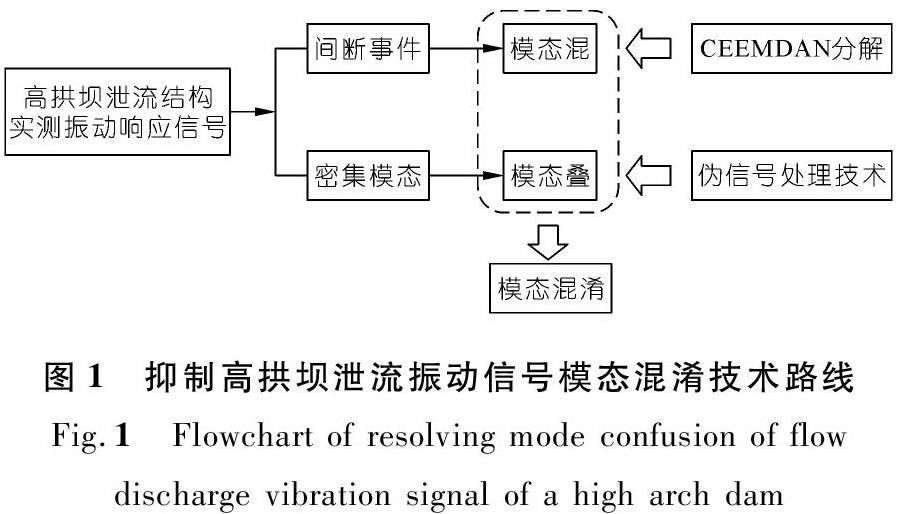
高拱坝泄流时结构的振动响应信号中既混有间歇高频干扰信号，又存在模态频率相近的信号，即实测信号存在间断事件与密集模态两方面影响，故而高拱坝泄流结构振动响应信号中存在模态混与模态叠的双重影响。据此，为合理获取结构的真实模态信息，本文针对上述2种模态混淆的影响方式，结合自适应噪声完备集合经验模态分解与伪信号处理技术分别对模态混与模态叠加以处理。技术路线如图1所示。

1.1 自适应噪声完备集合经验模态分解

自适应噪声完备集合经验模态分解法是María E.Torres等[16]于2011年提出的一种高效且平稳性较好的信号处理方法。该方法在集合经验模态分解的基础上，在信号分解的每一阶段添加自适应白噪声，使原始信号中的极值分布趋于平均，可有效遮覆其间的高频间歇及噪声等异常干扰信号，并通过自适应地调节加噪分量降低了分解过程的筛选次数。CEEMDAN能有效地抑制传统EMD分解中存在的模态混现象，使降噪后的振动信号分解结果更加精准，干扰成分更低。以某信号x（n）为例，进行CEEMDAN过程如下。

混合信号分别经过EMD及CEEMDAN分解，得到的结果如图2所示。

由图2（a）可知，EMD分解后得到的前3阶IMF均发生了混淆，难以辨识初始信号构成成分;由图2（b）可看出，经CEEMDAN分解后的第2阶IMF为脉冲干扰信号，第4阶为有交叠部分的间歇干扰信号，第6阶则是原始真实信号。因此，相比EMD方法，CEEMDAN在分解含有2种以上的干扰信号时仍能将瞬态信号与恒定模态有效分离，较好地提取出原始真实信号部分。然而，可同時从图中看出当两个单频信号的频率较为接近时，CEEMDAN无法对其引发的模态叠现象进行准确识别。

1.2 伪信号处理技术

当信号中存在2个及以上频率相近的混淆信号时，直接采用EMD算法对其分离将会导致模态叠。信号的可分解性与其相近本征模态函数的模态频比与幅值频比有关[21]，当混淆信号的频率之比fa/fb≥2时，各组合单频信号可经EMD算法进行分离，然而当混淆信号的频率之比0.5≤fa/fb<2时，采用EMD算法分解的IMF明显失真。假设某原始信号x（t）由频率为2.5 Hz、振幅为3 μm和频率为1.5 Hz、振幅为2 μm的理想简谐振动x1（t）和x2（t）组合而成，如公式（13）所示，其采样点长度2 000，采样频率100 Hz。

采用EMD算法对该信号x（t）进行分解，如图3可见，第一阶本征模态函数y1（t）（高频分量）发生模态混淆，且第二阶本征模态函数y2（t）（低频分量）与原始真实信号振幅不符。

因高拱坝大多都是密频结构，其相近模态频率比多在0.5～2.0，为较好地解决相近频率导致的模态叠，本文采用伪信号处理技术[22]对其加以处理。该方法是通过将一组易于被提取的IMF产生混淆的信号加入到原始信号中提升其信号序列的频部显著度，以模态混淆来抑制模态混淆现象发生的方法。因添加的伪信号为已知的单个正弦波信号，故可设法将其从提取的IMF中去除。相比带通滤波法通过不断缩小滤波频带区间的大小来抑制模态混淆，伪信号处理技术的优点在于较大程度上保障了信号的完备性和连贯性。

伪信号处理技术的计算步骤为：

该方法中，如何确定合适的振幅与频率参数，是合理选取伪信号的关键。相关研究[23]指出当伪信号频率取2fb≤fs≤2fa时，原信号低频频部不与伪信号发生混合，且高频频部与伪信号发生混掺，具有较好的分解结果。伪信号振幅a0的选择亦会影响分离性能，考虑到高拱坝泄流振动响应信号先前各模态分量的振幅值无法得到，故而采用原信号的最大振幅值当作伪信号振幅。在此，对式（13）引入伪信号m（t）=4sin（7πt），根据上述步骤对其进行分解，所获取的前两阶模态函数的时程过程如图4所示。

由图4可以看出，混合信号经伪信号处理后分解得到的两阶模态分量未发生模态混淆，因此可有效解决信号分解时所产生的模态叠问题。

2 抑制模态混淆的高拱坝模态参数识别理论

2.1 基于改进HHT结构模态参数识别方法

高拱坝实测泄流振动响应往往为非平稳信号，原始响应信号同时包含坝体自身自由振动与泄洪水流受迫振动，通过随机减量法从原始信号中提取坝体自由振动的模态信息后，应用Hilbert变换进行结构模态参数识别。本文将RDT与HHT方法相结合，先将原始信号经CEEMDAN分解，再采用RDT方法提取各阶分量的特征信息，最后运用Hilbert变换和最小二乘拟合识别结构频率与阻尼比。

2.2 高拱坝运行模态识别

针对传统HHT结构模态参数识别的模态混淆问题，应用带通滤波和伪信号处理控制CEEMDAN的分解过程，可避免因间断事件和密集模态造成的模态混淆。将改进后的方法称为基于流激响应伪信号处理的高拱坝运行模态识别方法，具体实施步骤如下：

（1）对降噪预处理后的实测高拱坝泄流振动信号，绘制归一化后总功率谱密度曲线。根据功率谱图选择合适频带对信号进行带通滤波，得到不同频带分量。

（2）绘制各频带分量的归一化功率谱图，判断频带内是否包含不同模态信息。

（3）若只含单阶模态信息，则直接对频带分量进行CEEMDAN分解，并选择与原始信号偏差系数小的模态作为本征模态函数;若包含多阶模态信息，则利用伪信号处理技术联合CEEMDAN分解将产生模态混淆的不同模态分离，再提取相应的本征模态函数。

（4）对得到的IMF进行随机减量处理，并用希尔伯特变换和最小二乘拟合识别模态参数。基于流激响应伪信号处理的高拱坝运行模态识别计算流程如图5所示。

3 案例分析

3.1 工程背景

位于四川省雅砻江下游的二滩拱坝为典型混凝土双曲高拱坝，坝顶高程1 205 m，最大坝高240 m，坝顶弧长774.65 m。为监测大坝的工作性态，在拱圈处2～38号坝段自左到右每隔5个坝段布置一个传感器（编号为B1-B7），坝体原型及测点分布情况如图6所示。该监测系统中动位移传感器为DP地震式低频振动位移传感器，其频响范围0.35～200.00 Hz，灵敏度为8～15 mV/μm。采用DASP数据采集和处理系统进行采样，采样时间为300 s，采样频率200 Hz，共采集60 000个数据点。在数据采集时，因实测拱坝流激振动响应易混入背景噪声和诸多干扰信号而淹没结构的真实响应数据，通过对比分析各工况的实测数据，选取3～5表孔全开时的典型泄洪工况，进行坝体工作参数模态识别。

3.2 高拱坝泄流结构运行模态参数识别

以典型泄洪工况下左坝肩B6测点数据为例，采用小波阈值-EMD方法对信号初步降噪预处理，消除信号中的毛刺。信号时程及其归一化功率谱密度曲线如图7所示。

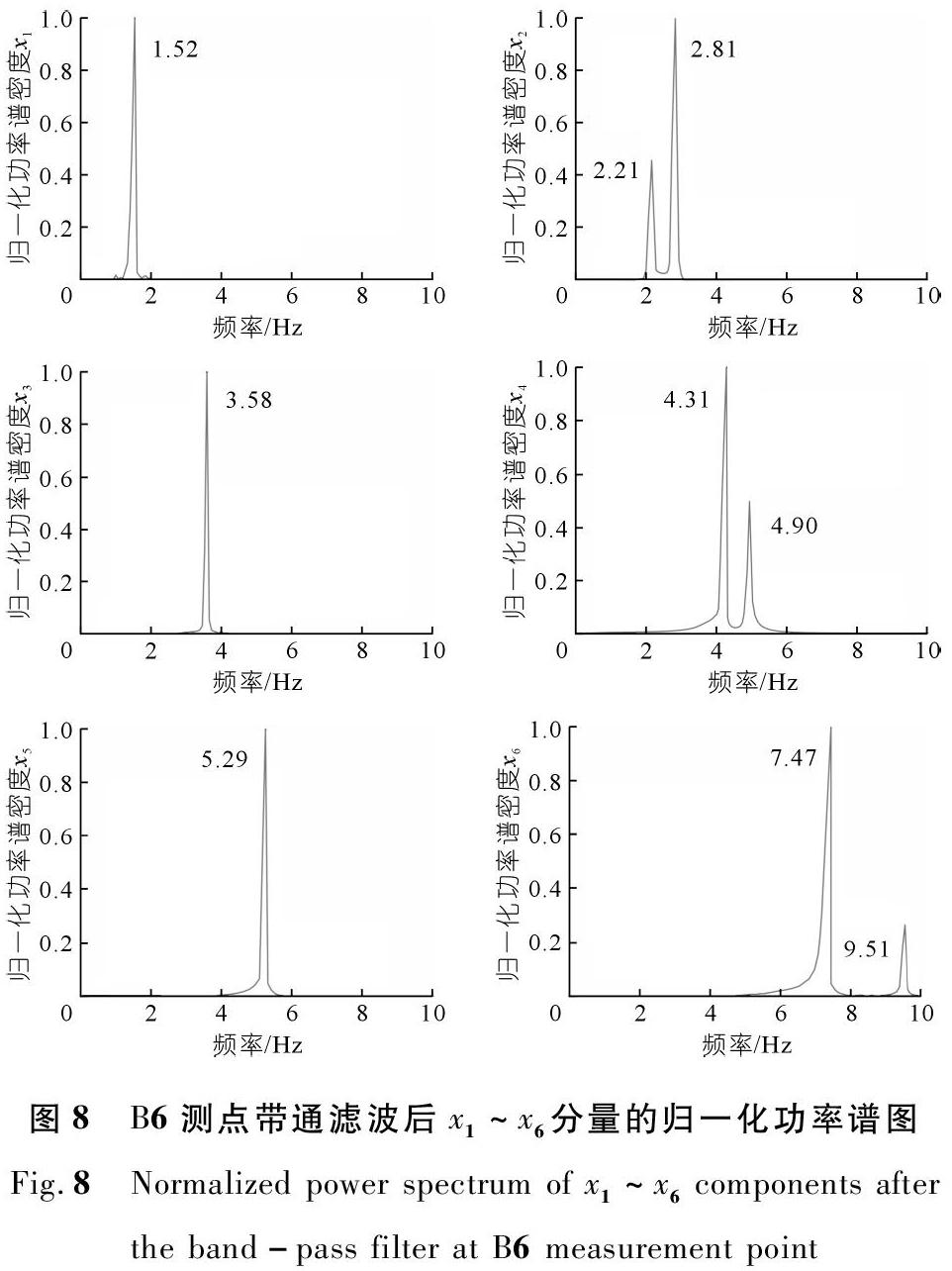
从图7可以看出，功率谱密度曲线在1.5，2.2，2.8，3.6 Hz处存在明显的峰值，据此取通带1～2，2～3，3～4，4～5，5～6，6～10 Hz进行带通滤波，得到分量x1，x2，x3，x4，x5和x6，并做出滤波后各分量的功率谱密度图，如图8所示。

从图8可以看出，x1、x3和x5分量的功率谱密度图为单峰曲线，故可对x1、x3和x5直接进行CEEMDAN分解，并选择与原信号偏差系数小的模态分量作为本征模态函数;而x2、x4和x6的功率谱密度图上含有2个峰值信号，表示这3个带宽信号分量中包含两种不同模态信息，将伪信号处理技术应用到x2、x4和x6分量中分别提取对应模态。

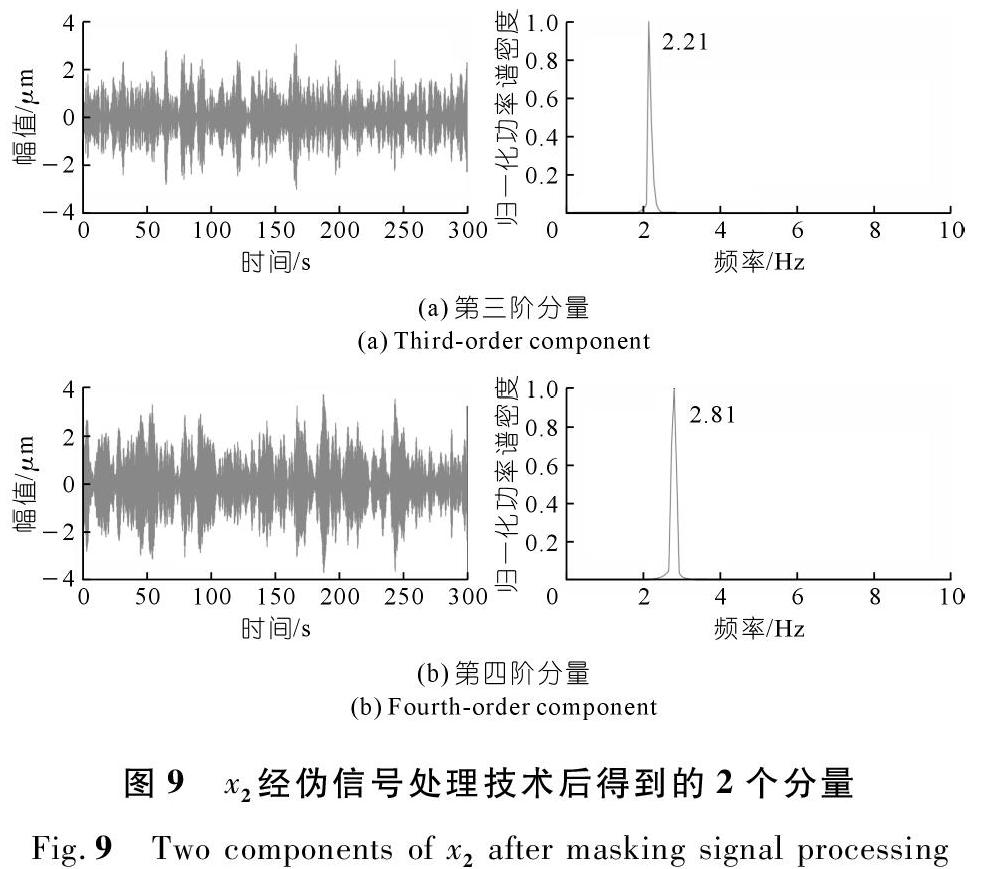
以带通滤波后的x2分量为例，从x2的功率谱密度曲线可以看出在2.2 Hz和2.8 Hz处存在峰值，引入伪信号m（t）=4.5sin（9πt），其中伪信号的频率取4.5 Hz、幅值取x2的最大振幅4.5 μm。经伪信号处理技术后得到x2不同分量时程图及功率谱密度图见图9。图中两个分量的功率谱密度图均为单峰曲线，表明伪信号处理技术有效解决了信号分解中的模态混淆问题。

同理，对x4和x6分量进行处理即可得到B6测点原始信号的前10阶模态分量。最后，对各IMF应用随机减量法提取出每个分量的自由衰减响应，并用Hilbert变换及最小二乘拟合，获取幅值和相位随时间的关系，从而识别结构模态参数。对x2处理分解后的3阶及4阶模态分量进行RDT处理，及对衰减响应进行Hilbert变换后的对数幅值曲线如图10和图11所示。

为说明本文高拱坝模态识别方法的合理性，分别运用传统HHT法，特征系统实现算法（Eigensystem Realization Algorithm，ERA）及Ibrahim时域法（Ibrahim Time Domain，ITD）计算其模態参数，其中，由于B6测点位于拱坝一阶振型节点附近，该测点的实测振动响应识别不出第一阶模态信息，因此以固有频率为例识别的前10阶结果如表1所列。

文中方法识别的模态频率均在坝体统计频率范围内，且与ERA法和ITD法两种典型的辨识方法识别结果相近。传统HHT法未能识别4阶、7阶和10阶模态信息，且频率参数识别结果与统计结果相差较大;ERA方法能较准确识别结构前5阶固有频率，但随着阶次增加，由于ERA法本身定阶难的缺点，不能全面辨识出结构的频率值，从而影响结构的工作模态识别结果;ITD法能较准确识别出频率信息，但对高阶模态进行拟合阶次时模态定阶时常成为问题。相比以上方法，改进后的HHT法能有效抑制模态混淆，避免模态信息丢失，并有效提高参数识别精度，适用于高拱坝泄流激振响应下的模态参数识别，具有显著的工程适用价值。

4 结 论

（1）在分析传统EMD分解中出现模态混淆的两种情况后，提出了应用CEEMDAN分解与伪信号处理技术分别对模态混与模态叠的处理方法，并通过仿真信号验证所用方法的有效性。

（2）针对水流激励下的高拱坝泄流结构工作特点，提出了基于流激响应伪信号处理的改进HHT高拱坝运行模态识别方法。运用RDT处理分解后的模态分量，使提取的自由衰减响应信息具有较高的可信度。此方法计算过程简单，相比传统HHT方法可有效避免模态信息丢失并能准确辨识出结构的模态参数。

（3）工程实例分析结果表明，所提方法可合理提取流激响应下高拱坝的运行模态参数，该方法具有良好抑制模态混淆的效果与较高的识别精度，为辨识高拱坝坝体工作健康状态提供数据支撑，可推广应用于其他大型密频结构工程的模态参数识别。

参考文献：

[1] 谯雯，罗佩，刘国明.基于自然激励技术和HHT变换的重力坝模态分析[J].水利学报，2014，45（8）：958-966.

[2] 胡金山.超高拱坝拱座及抗力体抗滑稳定研究[J].人民长江，2019，50（7）：138-143，164.

[3] 练继建，张建伟，李火坤，等.泄洪激励下高拱坝模态参数识别研究[J].振动与冲击，2007（12）：101-105，174.

[4] LI H K，WANG Y J，WEI B W.Inversion algorithm for the whole prototype dynamic displacement field of a high arch dam based on limited measuring points[J].Journal of Vibration and Control，2016，23（20）：3431-3447.

[5] BRINCKER R，ZHANG L，ANDERSEN P.Modal identification of output only systems using frequency domain decomposition[J].Smart Materials & Structures，2001，10（3）：441.

[6] 李启行，褚福磊.环境激励下的旋转机械工作模态参数辨识[J].机械工程学报，2019，55（19）：28-34.

[7] ASAYESH M，KHODABANDELOO B，SIAMI A.A random decrement technique for operational modal analysis in the presence of periodic excitations[J].Proceedings of the Institution of Mechanical Engineers，2009，223（C7）：1525-1534.

[8] HUANG N E，SHEN Z.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London，Series A，1998，454：903-995.

[9] 李火坤，练继建.高拱坝泄流激励下基于频域法的工作模态参数识别[J].振动与冲击，2008（7）：149-153，194.

[10] 田鹏明，连俊义，张凤.随机减量法在工作模态参数识别中的应用研究[J].机电工程技术，2012，41（6）：105-108.

[11] HUANG N E，STEVEN R L.A new view of nonlinear water waves：The Hilbert Spectrum[J].Annual Review of Fluid Mesh，1999，31（2）：417-457.

[12] 汪泉，李德忠.基于EEMD的水轮机摆度信号特征提取分析[J].人民长江，2017，48（5）：96-100.

[13] 李火坤，张建伟，练继建，等.泄流条件下的溢流坝结构原型动力测试与模态参数识别[J].中国农村水利水电，2009（12）：99-102，105.

[14] 魏博文，钟紫蒙.基于改進小波阈值-EMD算法的高拱坝结构振动响应分析[J].水利水运工程学报，2019（4）：83-91.

[15] WU Z H，HUANG N E.Ensemble empirical mode decomposition：a noise assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1（1）：1-41.

[16] TORRES M E，COLOMINAS M，SCHLOTTHAUER G，et al.A complete ensemble empirical mode decomposition with adaptive noise[C]∥2011 IEEE International Conference on Acoustics，Speech and Signal Processing（ICASSP），2011.Prague：IEEE International Conference on Acoustics：4144-4147.

[17] 胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动·测试与诊断，2011，31（4）：429-434.

[18] 张建伟，江琦，赵瑜，等.一种适用于泄流结构振动分析的信号降噪方法[J].振动与冲击，2015，34（20）：179-184.

[19] 练继建，荣钦彪，董霄峰，等.抑制模态混叠的HHT结构模态参数识别方法研究[J].振动与冲击，2018，37（18）：1-8.

[20] 张秀锋，王勇.基于EEMD和伪信号技术的涡街信号处理方法[J].合肥工业大学学报（自然科学版），2017，40（11）：1452-1457.

[21] 郑近德，潘海洋，杨树宝，等.广义变分模态分解方法及其在变工况齿轮故障诊断中的应用[J].振动工程学报，2017，30（3）：502-509.

[22] RYAN D，KAISER J F.The use of a masking signal to improve Empirical Mode Decomposition[C]∥IEEE International Conference on Acoustics，Speech and Signal Processing，2005.Philadelphia：IEEE International Conference on Acoustics：485-488.

[23] 李成业，刘昉，马斌，等.基于改进HHT的高拱坝模态参数识别方法研究[J].水力发电学报，2012，31（1）：48-55.

（编辑：郑 毅）