长江流域洪水概率预报业务化方法探讨
2021-10-18张俊杨文发牛文静张涛
张俊 杨文发 牛文静 张涛

摘要:当前长江流域洪水预报业务是基于确定性预报思路开展的,给调度决策者提供的风险信息有限,因此亟待开展概率预报应用研究。目前国内的概率预报多处在研究阶段,未形成完善的、实用的业务化方法。在综述长江洪水预报现状和国内外概率预报研究进展的基础上,从基本原则、模型方法库构建、业务流程、成果形式等方面提出了一种洪水概率预报业务化的成套技术体系,可为长江流域洪水概率预报业务的开展提供参考。
关 键 词:洪水预报;概率预报;模型库;作业预报;业务流程
中图法分类号:TV124
文献标志码:A
文章编号:1001-4179(2021)09-0011-05
DOI:10.16232/j.cnki.1001-4179.2021.09.003
0 引 言
习总书记在2018年考察长江时指出水患仍是中华民族的心腹大患,长江是中华民族的母亲河,虽然流域内已陆续建成了具有巨大防洪库容的控制性水库群,但由于暴雨洪水时空分布的复杂性,防洪减灾依旧是长江流域的头等大事。科学准确的洪水预报,对于流域水资源管理、防洪减灾、洪水资源化等具有重要作用。长江流域洪水预报自20世纪50年代起步[1],从应用相关图、谢尔曼单位线、降雨径流指数、马斯京根演算、大湖演算等传统预报方法开始,经过几十年的发展,不断探索新理论、新方法,并通过与国内外科研院所合作,引入了分布式新安江、DDRM、SWAT、RS Minerve、MIKE11等分布式水文模型及水力学模型。目前,在“水文气象耦合、短中长期嵌套、预报调度结合”的技术思路指引下,已构建了以重要水库、防洪对象及干支流控制断面为节点,满足各类对象防洪目标及需求的长江流域预报河系31个,预报节点400余个,水库调度节点60多个,预报方案760条套,基本实现了长江流域的全覆盖。
总体上,依托现有的洪水预报方法,长江流域预见期72 h内的水位流量预报达到准确[2],其中城陵矶-大通各站水位预报平均误差均在0.2 m以内,关键性的预报能提前3~5 d准确预报,良好的预报成果为科学调度水工程、成功防御长江洪水发挥了有力的支撑作用。尽管如此,目前广泛制作和使用的长江流域洪水预报大多基于确定性思路,即以确定单一数值形式输出给用户,形式上易于理解,却忽略了水文预报过程中存在的不确定性。而如今对于流域综合管理和精细化调度操作的要求越来越高,该思路在近年来的综合调度实践中逐渐暴露出其提供的风险信息有限的短板。统计决策理论指出,只有考虑了预报不确定性的水文预报,其风险信息才是完备的[3]。概率预报方法通过使用概率分布对预报量进行刻画,描述了预报结果的不确定性,从而让决策者更好地评估风险,成为当前水文预报领域的研究热点之一。
中央关于防灾减灾“两个坚持、三个转变”的新理念中明确强调,新时代防灾减灾在坚持“以防为主,从注重灾后救助向注重灾前预防转变”的基础上,要“从减少灾害损失向减轻灾害风险转变”,清晰指出了预测预报是防洪减灾的核心前提,同时也对长江流域洪水预报提出了更高要求,即水文要素预报需向概率预报和风险预警拓展,显然原有单一的确定性预报模式已不能适应新需求,长江流域洪水概率预报业务化开展迫在眉睫。基于此,本文在综述长江洪水预报现状和国内外概率预报研究进展的基础上,从基本原则、模型方法库构建、业务流程、成果形式等方面提出了一种洪水概率预报业务化的成套技术体系,可为长江流域洪水概率预报业务的开展提供参考。
1 洪水概率预报研究现状
Stigler[4]于1975年首次提出了概率预报概念,他指出应当将点估计转变为分布的估计。概率预报研究兴起于20世纪90年代,Krzysztofowicz[5]提出的贝叶斯概率预报系统(BFS)是公认的通过确定性水文模型进行概率预报解决水文预报不确定的理论框架,美国海洋与大气管理局联合欧洲中期天气预报中心等机构于2004年发起了国际水文集合预报试验计划[6],此后研究者们陆续提出各种概率预报新方法,尝试了不同流域的水文概率预报试验,这些试验和应用证明了概率水文预报的价值和前景。纵观国内外关于洪水概率预报的研究途径,大体可分为两类:① 集合概率预报法,亦称为全要素耦合途径;② 基于确定性预报的概率预报法,也可称为总误差分析途径。
1.1 集合概率预报法
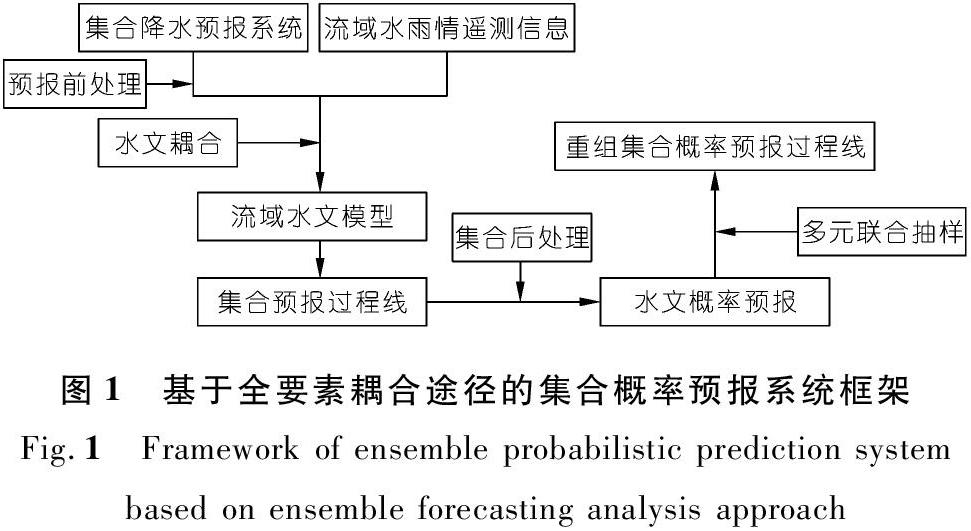
该预报法分别量化降雨-径流过程各环节的主要不确定性,如降雨输入、模型结构、模型参数、上游来水等不确定性,并进行耦合预报计算,将集合预报成果进行后处理,从而实现概率预报(见图1)。其输入信息一般是降雨、蒸发、模型参数等水文模型所需数据,着重于集合预报样本的充分模拟及后处理技术。该预报法的优点是能溯源预报的不确定性,但计算耗时,难以满足实时短期预报的要求。
基于Monte-Carlo抽样的概率预报法[7]、贝叶斯模型加权平均法(BMA)[8]、集合模型输出统计法(EMOS)[9]等属于该类范畴。
1.2 基于确定性预报的概率预报法
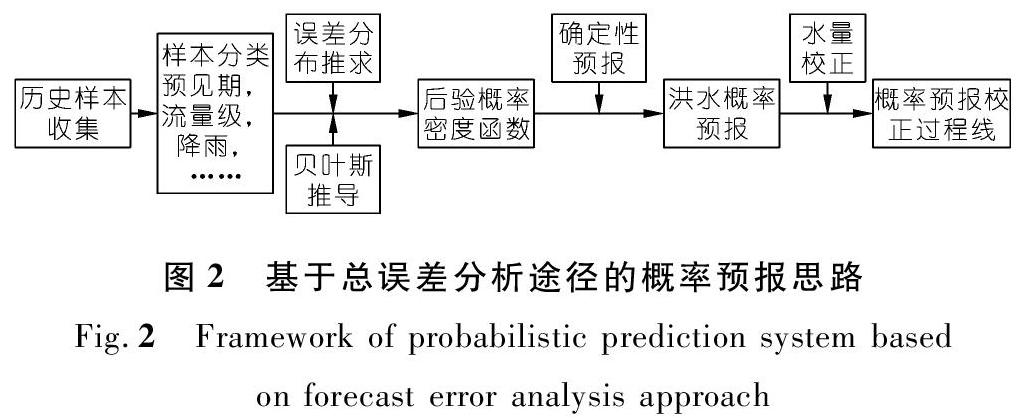
该预报法从确定性预报结果入手,直接对预报不确定性进行量化分析,推求预报量的分布函数,从而实现概率预报(见图2)。该预报法的输入信息是历史实况和确定性预报样本,着重于预报量的后验密度函数推求,其缺点是对历史样本依赖性强,但计算快捷,使用方便。
基于BFS框架提出的水文不确定性处理器(HUP)[10]、BP-BFS模型[11]、Coupla-BFS模型[12]是该预报法的代表性研究。近年来一些学者另辟途径,聚焦于分析不同预见期、流量級下预报误差的分布规律来量化预报的不确定性,从而实现分类分级概率预报,例如分布函数推求法[13]、最大熵法[14]、误差异分布法[15]等。
随着预报不确定性研究的深入与重视,当前世界上许多国家和地区已经建成水文集合概率预报系统,如美国国家气象局研制的概率水文气象预报系统[16]、欧洲的欧盟气象受限地区整合预报系统(COSMO-LEPS)[17] 等。从已有研究看来,水文集合概率预报这一前沿技术在国外发展迅速,已经进入业务化阶段,而中国目前的概率预报多处于研究探索阶段,尚未建成完善的实用技术体系,因此有必要开展长江流域概率预报业务化方法研究,进一步丰富和提高现有水文预报技术。通过比较现有洪水概率预报方法优劣,遵循便捷、实用原则,本文主要基于总误差分析途径开展长江流域洪水概率预报研究。
2 长江流域洪水概率预报的基本思路
2.1 预报业务化原则
长江流域洪水概率预报业务化的实现需要具备先进的概率预报模型或方法、严谨的建模步骤,但鉴于实时作业预报的时限要求,又需考虑计算的便捷性、实用性,总体应遵循以下几个具体原则:
(1)不影响现有预报流程,不额外增加预报员实时预报工作量,根据发布的确定性预报过程即可自动实现,计算耗时短;
(2)能反映当前发生洪水的主要不确性来源信息;
(3)能建立预报风险与决策影响的某种联系;
(4)方便嵌入至现有的预报系统中,具有完善的模型方法库和良好的展现形式。
2.2 洪水概率预报方法库构建
2.2.1 分布函数方法库
建立指数(EXP)、伽玛(GAM)、广义正态(GNO)、正态(NOR)、广义逻辑(GLO)、广义极值(GEV)、广义帕雷托(GPA)、耿贝尔(GUM)、皮尔森Ⅲ型(PⅢ)、Kappa(KAP)、韦克比(WAK)和Logistic(LOG)等水文分析中常用分布的概率密度函数、分布函数模型库;构建基于L-矩、极大似然估计(ML)的参数估计方法库;建立由K-S检验法、离差平方和(OLS)最小准则及赤池信息准则(AIC)等组成的分布函数拟合优度评价方法库。
通过构建分布函数方法库,为预报误差规律分析和最优分布函数推求提供基础工具。
2.2.2 概率预报模型方法库
通过比较现有洪水概率预报方法的优劣,选择以自主研发和技术引进相结合的方式,基于总误差分析途径研制长江流域洪水概率预报模型(见表1),并集成具有标准化、规范化接口的方法库,主要考虑以下几种模型。
(1)基于非参数估计的概率预报法(NPEFM)。
输入历史误差样本,若其样本系列分布函数假设检验的结果均不理想,可采用基于直方图、Rosenblatt估计、Parzen核估计或最近邻估计的非参数估算方法,分别推算预报误差的各种概率密度函数(窗宽的选取一般采用最小二乘交叉验证法来确定),绘制概率密度曲线图,并与样本散点系列拟合确定最优的非参数估计方法,计算其累计概率曲线,最终得出各频率对应的预报误差值数组R。
(2)基于误差分布动态参数推求的概率预报法(EDDPFM)。
在历史样本空间中分析分布函数参数与确定预报值(不同范围)的函数关系集合θ=Ψ(x),代入上述公式即可构建洪水概率预报模型。
(3)基于Copula函数的贝叶斯概率水文预报模型(Coupla-BFS)。
引进武汉大学的Coupla-BFS模型,丰富长江流域洪水概率预报模型库。该法的基本原理为:输入历史误差样本,通过调用分布函数方法库推求出历史空间中(Y0、Yt0、Mt0)的边缘分布,借助Coupla函数构建多变量联合分布;基于Coupla函数推导水文要素的先验密度解析表达式,反映实况过程不确定性;利用Coupla函数推导似然函数,反映预报模型预报能力;最后将先验密度和似然函数带入贝叶斯公式得到后验概率密度表达式,通过复化梯级求积的数值积分方法求解,构建Coupla-BFS模型。
2.2.3 洪水预报过程校正方法
为考虑洪水预报过程中各时刻水文要素(如流量)值之间的连续性和相关性,需对各节点独立的概率预报值进行联合重组抽样与校正,鉴于目前国内外还未有成熟的相关研究,因此以自主创新的方式创建基于水量的洪水预报过程线校正方法。
以流量级、降雨进行分类,从历史空间中计算m天(取决于最大预见期和预报对象次洪过程长度)洪水过程水量预报误差系列,采用非参数估计得到各保证率i下的水量误差比ri,根据不同预见期j预报误差特性设置不同校正比例pj,当设定置信度α时,则可计算洪水过程各预报时刻校正系数ki,j,公式如下:
将置信区间上下概率预报线分别乘以校正系数,即得到洪水概率预报校正过程线。
2.3 洪水概率预报的业务流程
长江流域洪水概率预报流程包括率定建模和实时作业预报两大部分。其中率定建模包括历史样本空间建立、洪水概率预报模型构建,实时作业预报包括确定性洪水预报制作、概率预报区间推求、典型预报线组推求、基于概率预报的水情预警发布等步骤,如图3所示。
2.3.1 历史样本空间建立
依据不同预见期、降雨量级和落区进行分类,收集包含预报断面实况流量和对应确定性预报值的历史样本,并计算预报相对误差样本系列,得到不同分类下的历史样本空间。
2.3.2 洪水概率预报模型构建
以历史样本数据为输入,调用概率预报模型方法库中的NPEFM、EDDPFM或Coupla-BFS方法,构建该预报断面不同分类条件下的洪水概率预报模型,并进行比较分析。若依据不同分类构建的预报模型结果差异较大,需量化预见期、流量级和降雨的不同分类条件(同一分类下各条件闭合),得到独立的洪水概率预报模型;若结果差别不大,则可采用统一的概率预报模型。
2.3.3 確定性洪水预报制作
根据常规作业预报流程,经实况水雨情监视、防洪形势分析、预见期降雨制作、河系自动计算、水库预调度信息掌控、区间交互与水库调洪计算、河道演算、人工经验校正确认等步骤,依据每日08:00实况,制作得到确定性洪水预报成果,并将预报结果进行入库与发布。
2.3.4 概率预报区间推求
以同一预报依据时刻制作的确定性预报过程结果为输入,分析未来各时刻对应的预见期以及预报降雨分类,选取不同的概率预报模型,一般取90%置信度计算各时刻的初始概率预报区间,调用水量校正法,对洪水预报过程(95%分位线、5%分位线以及50%分位线)进行校正,最终得到考虑洪水过程相关性的90%置信度下概率预报区间成果。
2.3.5 基于当前主要不确定性源的典型预报线组推求
剖析面临时段存在的几种主要不确定性来源,构建可能的输入边界情景,如上游水库某种调度方案、区间某种降雨強度等,依据确定性预报制作步骤计算得到典型预报过程线组,并量化其预报风险信息,以供会商决策时与概率预报区间以及确定性预报过程线进行比较。
2.3.6 基于概率预报的水情预警发布
综合研判多种预报信息,根据《长江主要控制站洪水预警发布标准表》,若预见期内某一主要断面流量或水位超过预警阈值的概率大于90%(需综合确定),则发布相应的洪水预警信息,相应地可以建立流域防洪应急响应启动标准。
2.4 成果形式
长江流域洪水概率预报成果形式设想如图4所示。其与传统概率预报研究成果的不同在于各预报过程线不是同一预见期下各时刻预报值的连线(不代表一次预报成果),而是依据同一预报时刻制作的未来不同预见期的次洪预报连续过程线,因而增加了成果的实用价值,另外,为反映面临时段的主要不确定性源,加入了典型预报线组,具体包含以下成果:
(1)确定性预报或概率中值预报,作为主推荐预报过程;
(2)依据当前可获得信息计算的90%置信预报区间,作为决策时考虑风险范围之用;
(3)典型预报过程线组,反映面临时刻主要不确定性来源的可能结果,供决策参考;
(4)预警信息,提供水文要素达到各级水情预警标准的概率风险信息。
以三峡水库为例,进行概率预报产品试验。采用EDDPFM法构建三峡水库5 d预见期的入库洪水概率预报模型,以“长江2018年第2号洪水”期间的7月9日为预报依据时间,制作未来5 d入库洪水确定性预报,作为主推荐预报过程;随后将其作为概率预报模型输入计算得到未来1~5 d预见期内的三峡水库入库流量概率预报区间,同时根据面临时段存在的主要不确定性来源即亭子口水库是否泄洪,构建可能的泄洪情况(第3 d开始按5 000 m3/s流量泄洪)作为输入边界情景,计算得到考虑亭子口泄洪的典型预报过程线,概率预报成果如图5所示。
综合分析上述三峡水库入库洪水概率预报成果可知:2018年7月9日,无论是90%概率区间或亭子口泄洪预报线,均显示三峡入库洪水在未来5 d内将有超过50 000 m3/s的风险,根据《长江水情预警发布管理办法(试行)》,发布长江上游三峡库区洪水蓝色预警,而确定性预报结果显示未达到预警发布标准。在本场编号洪水期间,概率预报产品较好地预报出50 000 m3/s以上量级的涨水过程,提前4 d发布出蓝色预警,比确定性预报更早提示出风险。
3 概率预报技术在长江流域的适用性分析
目前,在中国的防洪管理体系中,无论预报、调度决策、防洪响应等环节均是基于确定性的概念,风险管理的理念短时内难以被各级部门和人员完全接纳,另外概率预报的实施需要较大的历史预报样本空间,且要求预报员具备相对于传统确定性预报更强的专业知识,因此,长江流域概率预报业务全面铺开的难度较大,宜以典型断面重点示范的形式开展。
鉴于三峡水库、丹江口水库分别在长江防洪、供水方面的特殊性,建议可以三峡水库防洪调度、丹江口水库供水调度为典型,在实时预报调度业务中进行概率预报示范应用。考虑到概率预报的生命力在于“提供风险信息,优化决策方案,避免调度失误”,探索概率预报成果与调度风险的耦合点将是需要进一步研究的重点。
4 结 语
本文在总结国内外现有概率预报研究的基础上,针对长江流域洪水概率预报业务化需求,从基本原则、模型方法库构建、业务流程、成果形式等方面进行了初步思考,得出以下几点认识:
(1)鉴于实时作业预报的时限要求,长江流域洪水概率预报业务需注重计算的便捷性与实用性,具有自动实现功能;
(2)模型方法库应从分布函数方法、概率预报方法、洪水预报过程校正方法等方面,以自主研发和引进合作相结合的方式构建;
(3)洪水概率预报的业务流程包括历史样本空间建立、洪水概率预报模型构建、确定性洪水预报制作、概率预报区间推求、典型预报线组推求、基于概率预报的水情预警发布等步骤;
(4)长江流域洪水概率预报的成果包括主推荐预报过程线、概率预报区间、带风险信息的典型预报过程线组以及概率预警信息;
(5)实现概率预报成果与调度风险分析的有机结合,是进一步研究长江洪水概率预报业务化的重点。
参考文献:
[1] 王俊.长江洪水监测预报预警体系建设与实践[J].中国水利,2017(14):8-10.
[2] 程海云.洪水预报系统及其在工程调度中的作用[J].中国水利,2020(17):11-13.
[3] CHEN S T,YU P S.Real-time probabilistic forecasting of flood stages[J].Journal of Hydrology,2007,340(1-2):63-77.
[4] STIGLER S M.The transition from point to distribution estimation[J].Bull.Inst.Internat.Statist,1975(2):332-340,355-360.
[5] KRZYSZTOFOWICZ R.Bayesian theory of probabilistic forecasting via deterministic hydrologic model[J].Water Resources Research,1999,35(9):2739-2750 .
[6] SCHAAKE J C,HAMILL T M,BUIZZA R,et al.HEPEX:The hydrological ensemble prediction experiment[J].Bulletin of the American Meteorological Society,2006,3(5):1541-1547.
[7] KUCZERA G,KAVETSKI D,FRANKS S,et al.Towards a Bayesian total error analysis of conceptual rainfall-runoff models:characterising model error using stormdependent parameters [J].Journal of Hydrology,2006,331(1-2):161-177.
[8] 董磊華,熊立华,万民.基于贝叶斯模型加权平均方法的水文模型不确定性分析[J].水利学报,2011,42(9):1065-1074.
[9] ZHONG Y,GUO S,BA H,et al.Evaluation of the BMA probabilistic inflow forecasts using TIGGE numeric precipitation predictions [J].Hydrology Research,2018,49(5):1417-1433.
[10] KRZYSZTOFOWICZ R,Kelly K S.Hydrologic uncertainty processor for probabilistic river stage forecasting[J].Water Resources Research,2000,36(11):3265-3277.
[11] 李向阳,程春田,林剑艺.基于BP 网络的贝叶斯概率水文预报模型[J].水利学报,2006,37(3):354-359.
[12] 刘章君,郭生练,李天元,等.贝叶斯概率洪水预报模型及其比较应用研究[J].水利学报,2014,45(9):1019-1028.
[13] 翟劭燚,张晓雪,刘九夫.大伙房水库洪水预报误差分布规律分析[J].水文,2011,31(6):14-17.
[14] 刁艳芳,王本德,刘冀.基于最大熵原理方法的洪水预报误差分布研究[J].水利学报,2007,38(5):591-595.
[15] 梁忠民,蒋晓蕾,钱名开,等.考虑误差异分布的洪水概率预报方法研究[J].水力发电学报,2017,36(4):18-25.
[16] KRZYSZTOFOWICZ R.Probabilistic hydrometeorological forecasts:toward a new era in operational forecasting[J].Bull Amer Meteor Soc,1998,79(2):243-251.
[17] CLOKE H L,PAPPENBERGER F.Ensemble flood forecasting:a review [J].Journal of Hydrology,2009,375(3-4):613-626.
(编辑:谢玲娴)
