基于改进万有引力搜索算法的南中环桥模型修正

2021-10-18秦世强甘耀威康俊涛

振动与冲击 2021年19期

秦世强，甘耀威，康俊涛

(武汉理工大学土木工程与建筑学院，武汉 430070)

建立一个准确、能够代表实际结构行为的有限元模型对桥梁状态评估和监测有着重要的作用。然而，按照设计图纸建立的初始有限元模型，由于模型简化、结构设计参数的不确定性、结构退化或损伤等因素的影响[1]，往往难以代表实际结构行为。因此，需要对初始有限元模型进行修正，以降低结构响应的有限元计算值与实测值之间的相对误差。有限元模型修正的本质是一个优化问题，其目标函数是由结构响应有限元计算值与实测值的残差函数构成。对于桥梁结构模型修正的目标函数，通常具有多维、高度非线性和多个局部极值点的特征；传统搜索算法如梯度算法、牛顿迭代法在处理这类问题时，容易陷入局部最优，难以获得目标函数的全局最优解[2]。近年来基于智能优化理论的粒子群算法[3]、遗传算法[4]、猴群算法[5]、万有引力搜索算法(gravitational search algorithm ，GSA)[6]等迅速发展，相比传统搜索算法，智能进化算法在处理非线性、多极值等问题时具有一定的优势。Alkayem等[7]对基于智能算法的有限元模型修正进行了全面的综述，总结了各类单目标优化算法和多目标优化算法在有限元模型修正中的应用现状；同时，作者指出提升智能算法的搜索精度和效率，仍是模型修正和损伤识别领域一个值得研究的方向。

GSA[8]是Esmat Rashedi等提出的一种元启发式算法，是一种模拟物理学中万有引力的新的优化算法。它通过种群中粒子间的相互作用来指导群体进行智能优化搜索；已有研究表明[9]：GSA的收敛性明显优于粒子群算法、遗传算法等仿生优化算法。但是GSA依然存在着容易早熟、后期迭代速度慢、不易跳出局部最优解等问题。针对GSA的上述问题，已有文献提出了一些改进措施。谷文祥等[10]提出一种新的局部搜索算法并结合GSA求解流水线调度问题，有效的避免算法陷入局部最优值，提高了解的质量，验证了所得算法的有效性；李超顺等[11]结合粒子群算法的运动特点提出了改进的引力搜索算法，并将其应用到励磁控制系统PID(proportional-integral-derivative)参数优化，并与传统群体优化算法进行了充分对比试验，验证了其优化算法的有效性；李沛等[12]在GSA的速度更新部分引入粒子群算法中的记忆和群体信息交流功能，并提出了基于权值的粒子惯性质量更新公式，验证了所提算法能有效规划出无人机的最优航路；蒋建国等[13]针对基本GSA在处理优化问题时会出现发散的情况,通过限制粒子的速度同时更改算法中的参数，并将改进的GSA运用到边坡稳定性分析中，搜索出临界滑动面并结合极限平衡法计算出相应的最小安全系数，并验证了其具有更好的优化性能。本文在上述研究的基础上，结合遗传算法提出一种改进的GSA，利用荷载试验结果并结合Kriging代理模型，实现了一座钢混叠合梁组合式系杆拱体系桥梁的模型修正。

1 基于Kriging模型的模型修正

有限元模型修正的本质是通过改变模型中的结构设计参数，减小有限元计算值与实测值之间的误差。因此，模型修正的目标函数可以定义为

(1)

式中：x为待修正的设计参数；ri(x)为第i类结构响应计算值与实测值之间的残差函数；m为模型修正中考虑的结构响应的类型种数；αi为不同残差函数的权重系数。

为获得式(1)所表达的目标函数在设计空间内的最小值，一般需通过迭代法求解。然而，由于结构响应与设计参数间隐函数的关系，使得每次迭代均需要调用有限元模型来计算残差函数，这一过程十分耗时，特别是对复杂的桥梁结构有限元模型而言。基于代理模型的模型修正方法因此得以发展；常用的代理模型包括多项式响应面[14]、径向基函数[15]、Kriging模型[16]等。有研究表明[17]：Kriging模型不仅可以给出设计空间内任意一点的预测值，同时能给出该点的预测误差。基于Kriging模型的模型修正的主要流程可分为3个步骤:① 需要用初始有限元模型得到结构的响应和设计参数样本，可通过试验设计[18]完成，常用的试验设计有中心复合设计、D最优设计、均匀设计和拉丁超立方设计等；② 利用得到的响应和设计参数样本生成Kriging模型并做精度测试；③ 基于优化算法寻找目标函数在设计空间内的最小值。

Kriging代理模型是由确定性的回归模型和随机过程两部分组成，结构响应矩阵Y(x)可以用Kriging模型表达成设计参数x的表达式，公式为

(2)

2 基本万有引力搜索算法

GSA是一种模拟万有引力定律的智能搜索算法。GSA中每个粒子都可以看作一个个体，每个粒子都具有自身的位置和移动速度，并且可以保留迄今为止粒子所能找到的最优位置以及所有粒子当前能找到的全局最优位置。在标准的GSA中，粒子i和粒子j之间的引力可表示为

(3)

式中：pd,i(t)为在t时刻第i个个体在d维空间中所在的位置；Mpi(t)为t时刻受力个体i的质量；Maj(t)为t时刻施力个体的质量；ε为一个很小的常数；Rij(t)为粒子i与j之间的欧几里得距离，可表示为

(4)

G(t)为在第t时刻的万有引力常系数，可表示为

(5)

式中：G0为常系数的初始值；α为下降系数；T为总迭代次数。因此，第i个个体在d维空间中的合力可表示为

(6)

式中：N为粒子种群的个数；rand则为0到1的随机数。t时刻时粒子i的加速度可表示为

(7)

式中，Mii(t)为t时刻粒子i的惯性质量。粒子i在d维空间中的移动速度以及位置的更新可以表示为

Vd，i(t+1)=rand×Vd，i(t)+accd，i(t)

(8)

pd，i(t+1)=pd，i(t)+Vd，i(t+1)

(9)

式中，Vd，i(t)，pd，i(t)分别为第t次粒子移动速度和位置。每个粒子的质量是通过第t次的个体适应度计算得到，可表示为

(10)

式中：fiti(t)为第t时刻个体的适应度；worst(t)和best(t)分别为第t时刻种群中个体最差和最好的适应度。假设个体的引力质量、惯性质量和个体的质量相等，则有

Mai=Mpi=Mii=Mi,i=1,2,…,N

(11)

(12)

可知当粒子的适应度较优时，粒子的质量就较大，自身的移动速度就会较慢，会不断吸引适应度较差的粒子向适应度更好的位置移动。

3 改进GSA

在GSA的过程中，当两个粒子之间的距离较近时，粒子就可能陷入局部最优解并且很难跳出局部最优值，从而降低了搜索效率。本文结合遗传算法提出一种改进的GSA。首先通过对初始种群适应度计算，按照适应度的大小对初始种群中的粒子进行排序。然后将初始种群分为优解组和劣解组两组，对优解组进行随机交叉的操作，对劣解组进行变异的操作；将交叉变异得到的新种群与当前迭代中的初始种群进行重新排序，取适应度值最好的前一半种群作为本次迭代后的更新种群；并且引入了概率控制，在整个算法初期，主要进行全局搜索，加大搜索范围，在后期则进行局部挖掘，增加搜索结果的精度，通过控制进行交叉变异操作的概率，能够有效地发挥全局搜索和局部挖掘的能力。

首先生成种群数量为N的初始种群，计算所有粒子的适应度值fitness(t)并且进行排序，然后根据适应度将适应度较好的一半粒子放入到优解组当中，再将另一半较差的粒子放入到劣解组当中，将优解组进行遗传交叉操作，用优解组的父代种群产生优良的子代种群，并且在本改进算法中进行交叉操作的两个粒子是随机选取，可表示为

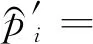
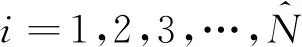
(13)

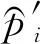
劣解组采用变异操作，通过变异操作产生优良的子代，充分利用每个个体；变异可表示为

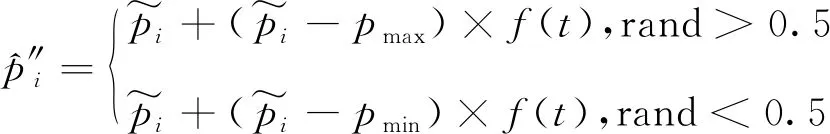
(14)

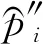
对改进算法流程描述如下，改进算法的流程图，如图1所示。

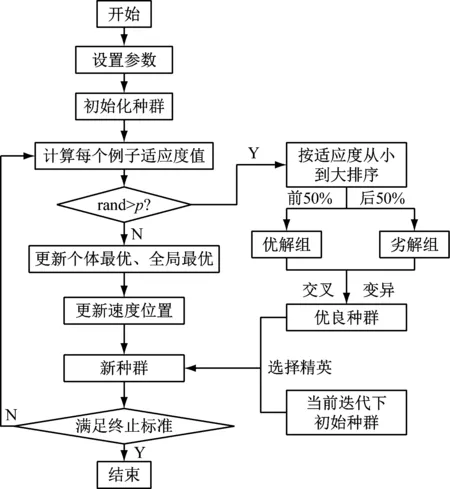
图1 算法流程图

步骤1设置算法初始参数。

步骤2随机生成初始种群。

步骤3计算初始种群的适应度，初始化个体最优值和全局最优值。

步骤4根据概率控制判断是否进入遗传交叉和变异，若rand>p则进入步骤5，否则进入步骤7。

步骤5进行分组策略，根据适应度优劣排列粒子顺序，将适应度较好的一半粒子放入优解组进行遗传交叉操作，将适应度较差的另一半粒子放入劣解组进行变异操作。

步骤6进行精英策略，将优解组产生的子代和劣解组产生的子代合并为一组，再与当前迭代次数下的初始种群建立一个扩大种群，将扩大种群按适应度排序，选取适应度较好的一半种群作为精英种群参加下一轮迭代。

步骤7用式(8)、式(9)更新粒子的速度与位置。

步骤8更新粒子个体最优值，全局最优值。

步骤9判断是否满足迭代终止标准，若算法迭代次数达到最大迭代次数T，则终止算法，否则跳回步骤3。

4 算法仿真测试

4.1 参数设置

为了验证改进GSA的效果，基于测试函数对粒子群算法、GSA和改进GSA进行对比分析。其中粒子群(particle swarm optimization，PSO)算法是由Kennedy等[20]提出的模拟鸟群觅食行为的一种群体协作优化方法。在参数设置上，为保证各算法可比性，3个算法种群规模均取30，函数维度均取10，最大迭代次数取1 000。对于PSO，其学习因子c1和c2分别为1.5和0.5，惯性常数取0.726，上述参数是标准PSO的默认参数，已被证明适用于各类优化问题；对于GSA和本文算法，其万有引力系数G0皆取10，下降系数α皆取20。

4.2 测试函数

选取5个函数标准测试函数，将本文改进的算法与PSO和GSA算法进行比较。其中f1为单峰函数，主要用来测试算法的精度与收敛速度；f2为多峰函数。当两个函数维度取2时，函数图像如图2所示。两个函数用来测试算法的收敛速度和精度，以及跳出局部最优解和全局搜索的能力。两个测试函数的全局最优值均为xi=0,(i=1∶n),f(x)=0。为了消除随机性可能对算法造成的影响，每个测试函数都用3种算法运行了100次，试验所处环境为：MATLAB R2018a，CPU为i5-9400F@2.90 GHz。以均值和方差作为算法的评判标准。均值表示算法的精度，方差则能反映得到结果的稳定性，收敛曲线能反映算法的收敛速度。f1为单峰值球函数，所以结果越接近0就表示越精确，故设置成功率来显示其优化的效率，当适应度小于1×10-20，就认为搜索成功；f2函数在最优值附近还有许多局部极小值，故当适应度分别小于1×10-10则认为搜索成功。

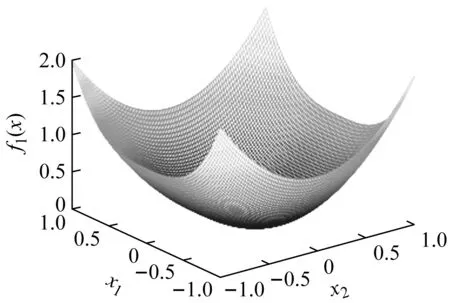
(a) Sum of different power函数图像

(1) Sum of different power函数：x∈[-1,1]

(15)

(2) Ackley’s Path函数：x∈[-1.5,1.5]

(16)

4.3 仿真结果分析

为了比较改进GSA，PSO和GSA算法的优劣，图3列出了两种测试函数的平均适应度曲线图，各算法100次搜索的统计结果，如图3所示。从平均适应度曲线的数据可以看出，改进的优化算法在精度上都要优于PSO和GSA算法，改进算法收敛时的结果对于f1测试函数都要小于1×10-20，对于测试函数f2其收敛时的精度也明显高于另外两种算法。

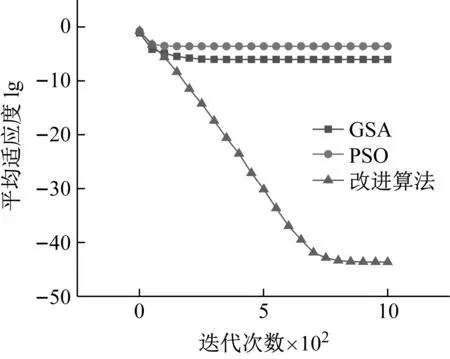
(a) f1

对于f1函数改进的优化算法得到的适应度相比其他算法其探索点的精度显著提高，在优化的成功率上，其达到数量级1×10-15以下的成功率为100%远远高于其他优化算法。对于测试函数f2改进算法探索到最优位置的成功率接近100%。且测试函数f2其全局最优值相对于局部极小值的适应度相差很小且局部最优值数量较多，因此很难找到最优位置，改进GSA的成功率有98%，其他算法则很难找到最优值；这表明改进GSA显著提升了跳出局部最优解的能力。将3种算法相对于两种测试函数的计算效率进行了对比，列出了完成一次寻优操作所需时间具体时间，如表1所示。可以看到，相比基本GSA和PSO算法，由于改进GSA算法加入了交叉变异等操作；因此，其效率上不占优势，但也未显著增加计算时间。

表1 计算效率对比

5 南中环桥模型修正

5.1 工程概况

南中环桥是连接太原市东西城区的重要桥梁，如图4所示。该桥主桥结构体系为组合式系杆拱、钢管混凝土蝶形拱桥，跨径布置为(60+180+60) m。主桥跨中为钢混叠合梁段，全长92 m，主梁高为3 m；主桥边跨60 m及中跨44 m梁段，采用的是混凝土箱梁，梁高为3.0～6.5 m。主桥标准断面宽度53 m，跨中宽度为71 m。主跨是由4根主副拱肋组合而成的下承式钢管混凝土拱桥，主拱肋外倾16°，矢跨比为1/4.326；副拱肋外倾26.882°；主拱肋和副拱肋之间利用拉杆连接。

图4 南中环桥

5.2 荷载试验概况

南中环桥荷载试验分为静载试验和动载试验两个部分，静载试验主要测试桥跨结构在试验车辆静载作用下的位移；动载试验主要测试结构的固有振动特性和冲击系数。限于篇幅，仅介绍与模型修正相关的试验工况。模型修正共选择了两个静载试验工况(A-A、B-B)，测试在车辆下主梁和主拱关键截面的位移。图5为桥梁立面图及位移测点布置图。静载试验车辆为40 t三轴载重汽车，轴距为(1.8+3.3) m。动力测试部分，为获取桥梁的固有振动特性，利用加速度传感器测试主梁在环境脉动荷载下的三向加速度响应。在主梁纵向平均每14 m布置一个加速度测点，采样频率为80 Hz。利用测试得到的加速度响应，结合模态识别算法可以获得桥梁的频率、阻尼比和振型。静力位移、频率的试验值和计算值的对比结果，如表2和表3所示。从表2和表3可知，位移最大相对误差达28.19%，频率的最大相对误差达到9.51%；其中，计算值是根据Midas Civil初始有限元模型计算得到的。该模型按设计图纸建立，全桥共有8 322个单元，6 118个节点，其中主副吊杆和斜拉杆采用桁架单元，其余部分皆用梁单元模拟。主梁采用梁格法模拟，钢管混凝土拱采用联合截面模拟；吊杆张拉时考虑几何刚度贡献，边界条件按设计图纸设置。

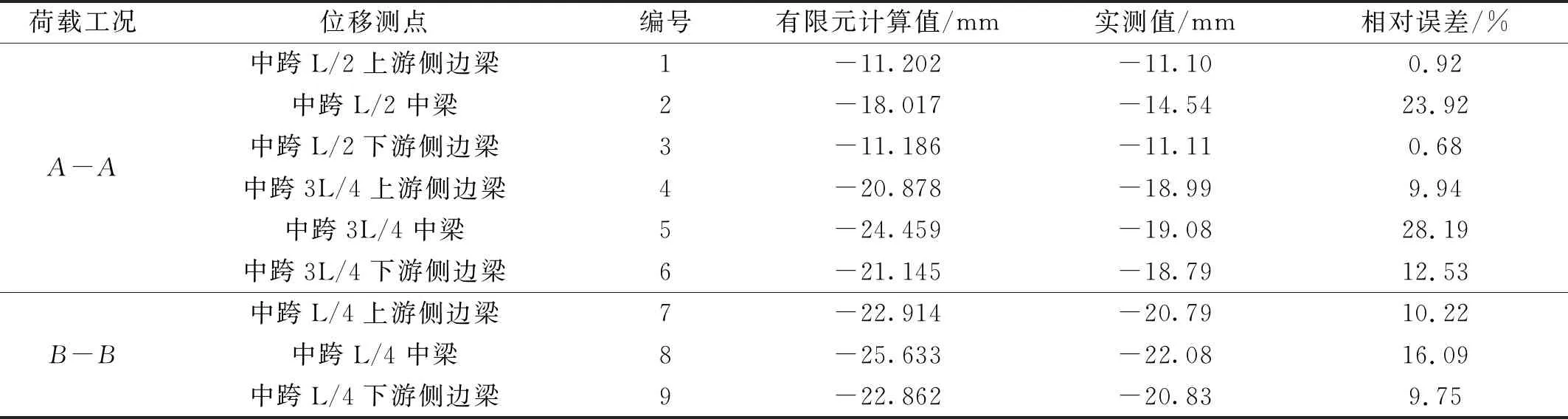
表2 两种工况下各测试截面的位移计算值和试验值

表3 桥面系实测自振频率及其计算频率

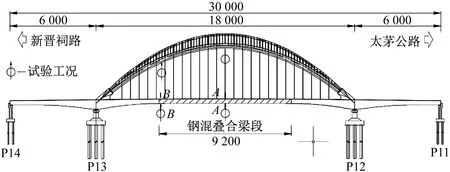
图5 桥梁立面图及位移测点布置图(cm)

主梁前两阶竖向振型计算值和试验值的对比，如图6所示。对应的模态置信值(modal assurance criterion, MAC)分别为0.946和0.963；这表明试验振型与计算振型吻合良好，反映试验数据可靠。上述分析表明：初始有限元模型对结构真实刚度分布模拟不够准确，需要通过模型修正，从而更好地代表实际结构行为。

(a) 主梁二阶振型

5.3 Kriging模型建立

为了提高模型修正迭代效率，利用Kriging模型替代有限元模型预测计算值。首先选择修正参数，然后利用拉丁超立方抽样获得参数在设计空间的分布，最后建立Kriging模型并评估其精度。

在修正参数选择方面，因为该桥为预制构件所以截面误差一般较小，故截面惯性矩不作为修正参数。在建立有限元模型时对于整个桥梁进行了简化，并没有建立节点板、螺栓等构件，所以在结构的质量分布上会存在影响，而一些细部的加劲肋则会影响到模型的整体刚度，因此将参数的选择范围定在各个构件的质量密度和弹性模量上。本文分别选择了钢管拱主拱、钢管拱副拱、钢混叠合梁段、混凝土段和挑臂5个构件的弹性模量和质量密度共10个参数进行敏感性分析。结合敏感性分析结果，最终选取钢管拱主拱弹性模量E1、钢管拱主拱密度ρ1、钢混叠合梁段弹性模量E2、钢混叠合梁段密度ρ2、混凝土段主梁弹性模量E3和混凝土段主梁质量ρ3这6个参数作为待修正参数，其初始值分别为2.06×108kN/m2，78.5 kN/m3，2.06×108kN/m2，78.5 kN/m3，3.45×107kN/m2，26 kN/m3。

采用拉丁超立方抽样法对选定的修正参数进行试验设计，对6个设计参数进行了81次抽样，参数的抽样范围设定在±30%以内，再将设计得到的修正参数分别代入初始有限元模型中得到对应工况下的位移以及频率响应。以样本点作为输入，节点位移值及模态频率响应值作为输出构建Kriging模型。选取钢管主拱弹模E1、钢混叠合梁段弹模E2两个设计参数和该桥有限元模型一阶频率绘制三维Kriging响应面图。一阶频率对于修正参数E1和E2的Kriging响应面模型以及对应的均方误差(mean square error，MSE)，如图7所示。其中曲面为Kriging模型响应面，散点为样本点，可知样本点基本位于曲面上。从对应的MSE图可以看出，误差基本都不超过3×10-9，说明Kriging精度较高，可替代有限元模型进行结构响应预测。

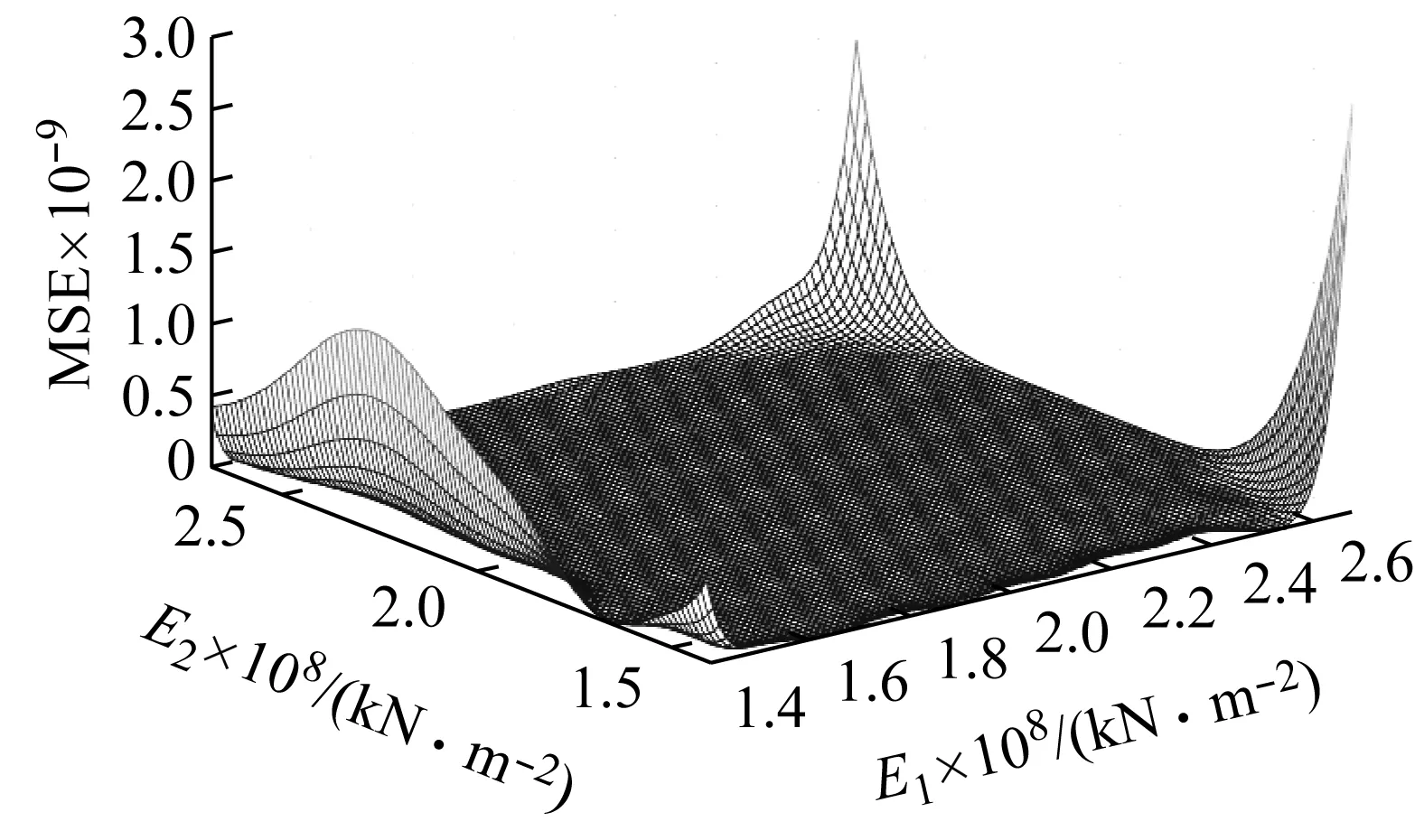
图7 一阶频率与E1、E2之间函数拟合图

5.4 数值验证

考虑到实际结构损伤位置是未知的，为了证明模型修正方法的有效性，首先利用南中环桥有限元模型进行数值验证。给参数E1,E2,E3设定数值损伤，其中：相较于初始值，参数E1,E2设定+10%的数值损伤，参数E3设定-10%的数值损伤，以未设损伤的模型代表初始有限元模型，施加损伤后的模型为真实的有限元模型。以3个设计参数作为输入，以前6阶频率作为输出，建立Kriging模型，然后以本文中的3种优化算法对建立的Kriging模型进行寻优，PSO算法仍取其默认参数；GSA和改进GSA算法的万有引力系数取为10，下降系数为20；各算法的种群规模均为30，最大迭代次数为1 000。其设计参数和频率响应的结果,如表4、表5所示。由表可知，改进算法3个设计参数的修正偏差修正前最高为11.11%，修正后误差都降到约0.1%；频率的响应值在修正前最大偏差达到1.78%，修正之后改进算法的最大误差仅为-0.024%。采用本文的改进算法结合Kriging模型的模型修正方法是有效的。其中改进GSA、GSA和PSO算法的计算时间分别为0.468 s、0.353 s和0.146 s。对于桥梁模型修正而言，每次迭代中最为耗时的部分是评估目标函数，即计算设计参数修改后的目标函数值，而算法所耗时间相对较少；因此，改进GSA的计算效率可以接受。

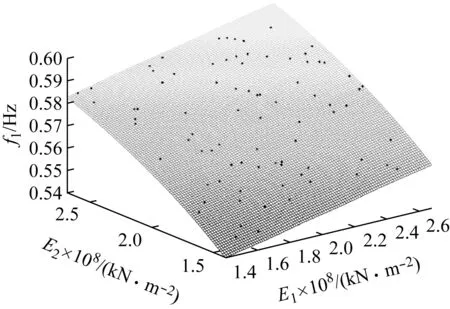
表4 参数修正前后对比

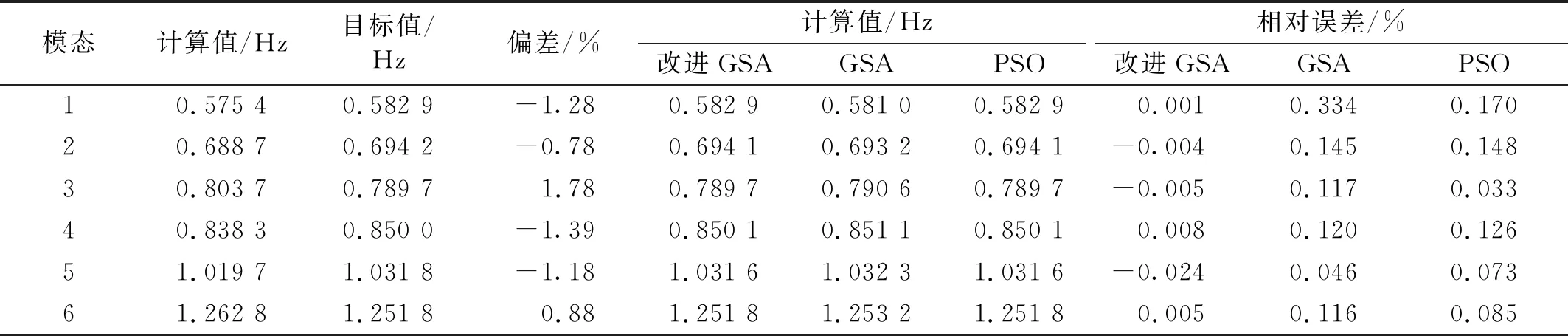
表5 频率修正前后对比

5.5 基于实测数据的模型修正

以位移残差和前4阶频率残差构建目标函数，分别利用改进算法、GSA和PSO对目标函数进行寻优，算法在参数设置上，PSO算法仍取其默认参数；GSA和改进GSA算法的万有引力系数取为10，下降系数为20；各算法的种群规模均为30，最大迭代次数为1 000。修正后的参数、频率和位移结果分别如表6、表7和表8所示。

由表6可知，参数钢管拱主拱弹性模量E1、钢混叠合梁段弹性模量E2、混凝土段弹性模量E3利用改进万有引力搜索算法的修正结果相较于初始值分别提高了13.27%，21.72%，24.37%，主要原因为在建立初始模型时对桥梁整体进行了简化，在建立有限元模型时并没有考虑局部加劲肋和横隔板，并且钢管拱以及钢混叠合梁段在实际桥梁中数量较多，所以有限元模型比实桥的刚度较低；钢管拱主拱密度ρ1的修正值都与实际值差别不大，都略微偏小；而钢混叠合梁段密度ρ2的修正值都比实际值偏大，混凝土段质量ρ3的修正值则比实际值都较为偏小，原因是在混凝土施工质量存在一定的离散性，使分布不均匀，并在模型修正中体现出来。需要指出的是，实际桥梁参数修正前后的变化参数修正前后的变化，仅表示模型整体刚度和质量分布与实际情况的差异，并非材料参数发生了变化，即修正后的参数可理解为等效弹性模量和等效质量密度。并且通过查看设计图纸可以得知钢混叠合梁段钢梁节段一的总质量为107 434.7 kg，而通过Midas Civil查询单元质量可知初始有限元模型钢梁节段一的总质量为103 025.2 kg，即有限元模型中的质量低估了约4.28%，这与钢混叠合梁段密度ρ2的修正值3.77%较为接近。

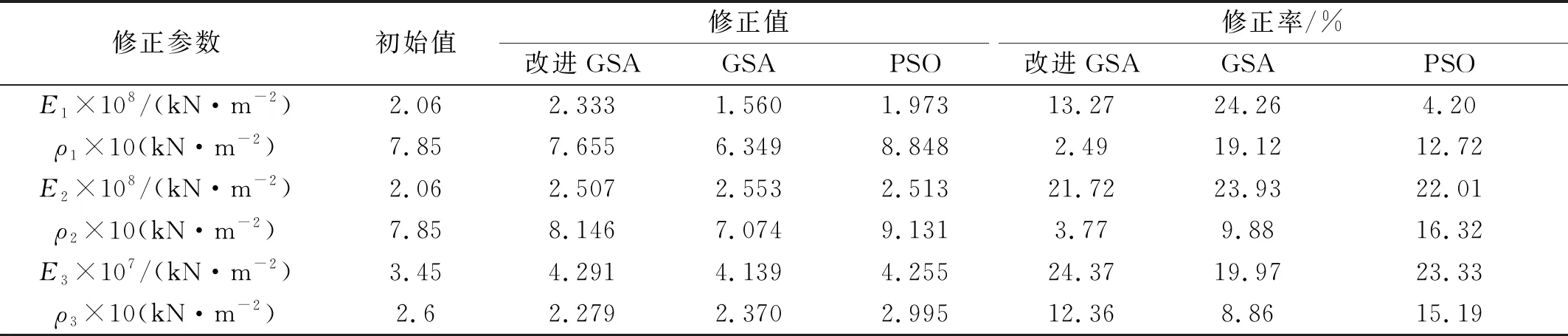
表6 参数修正前后对比

由表7可知，利用改进GSA、GSA和PSO修正后频率值的对比，其相对误差皆为修正前后计算值相对于实测值的误差。从整体看南中环桥的实测频率比计算频率都偏大，说明有限元模型的整体刚度都偏低，与参数的修正结果符合，修正后的频率值都有所提升，说明修正结果可作参考。相比初始模型，各算法修正后的频率相对误差均有不同程度降低，改进GSA取得了相对于PSO和GSA更好的修正结果。

表7 频率修正前后对比

由表8可知，3个优化算法修正后位移值的对比，除了节点1和节点3在修正前其计算值和位移值差距不大导致修正空间较小，其余7个节点都相对于修正前精度有明显的提高。整体上有限元模型计算值与实测值相比都偏大，也证明了有限元模型在整体刚度上都偏小，修正后结果都比修正前更加接近实测值。修正前，实测值与计算值的最大误差达到了28.19%，在修正后，改进算法所得结果的相对误差为13.62%，在精度上得到明显的提升，且GSA和PSO的修正结果相对误差分别为16.39%和15.90%，改进算法也比这两种算法修正精度要高。上述结果表明：经过模型修正，模型的位移值计算值和测试值更为接近，其相对误差减小，表明了修正后更能反映实际情况。相对于GSA和PSO，改进GSA的修正精度更高。