《JJG168—2018立式金属罐检定规程》中几何法罐底底量的计算方法
2021-10-18王松武
王松武
〔威海威洋石油公司 山东威海 264205〕
底量表作为储罐容量表的主要组成部分,其准确度能否达到罐容表不确定度要求,将影响整个罐容量表的准确度。《JJG168-2018立式金属罐检定规程》(以下简称《规程》)中底量的检定介绍了容积比较法和几何法两种检定方法。本文对几何法底量计算公式进行推导,对其存在的偏差问题进行分析验证并给出解决方法。
1 罐底为规则几何底的底量计算
《规程》中介绍的是不规则底的底量计算公式,在此先介绍一下规则圆锥罐底容积计算方法,并举例计算罐底任意一点的底量。规则几何底可看成一个标准的圆锥体,其上任一点对应的底量可看成圆柱体减圆台(圆锥)的体积,如图1所示,其阴影部分体积计算公式为:

图1 规则底量容积示意图

(1)
式中:H为罐底最高点,m;R为罐基圆半径,m;R2为圆台上半径,m;h为罐底任一点相对于下计量基准点高度,m;h0为下计量基准点相对于罐底低点高度。
例如:某罐基圆半径R=4.514 m,罐底高点H=0.067 m,下计量基准点h0=0.007 m,π≈3.14159。根据公式(1)求任一高度h的底量容积,计算结果如表1,对其数字修约形成底量表[1-2]。
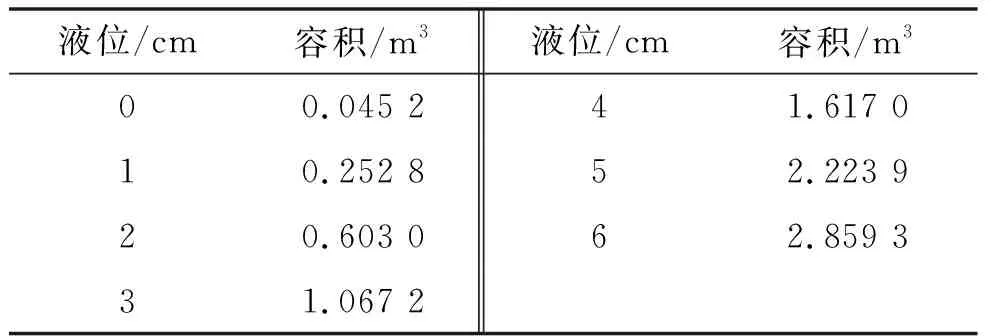
表1 底量计算结果
2 罐底为不规则几何底底量的计算
现实中罐底设计时一般按照坡度为15:1 000的锥形底设计。由于在施工和使用过程中基础不均衡下沉而导致罐底凹凸不平,其结构一般中间高四周低。以下主要进行不规则罐底量算法公式的推导。
2.1 测量点的确定及标高测量
测量点是在罐底确定等面积同心圆周长(I,II,III…,m)和相邻夹角相同的半径(0-1,0-2,0-3,…,0-n)的交点[3](详见JJG168-2018)。
设R为基圆半径,罐底由内向外的m个圆环的半径分别为:
将水准仪架设在罐底中心点附近,如图2所示[4],用标高尺直立于各测量点、罐底中心点和下计量基准点,由水准仪读出标尺读数,记录各测量点标高Bm,n,B0,B基。

图2 测量点标高示意图
2.2 底量计算公式推导
为了公式推导易于理解和推算,先计算各同心圆圆周上的测量点标高Bm,n的算术平均值Bm,然后再计算出Bm、B0、B基相对罐底最低点的实高hm(m=1…m),h0,h基,设R为罐基圆半径,罐底凹和凸两种情形下各圆环体积见图3。
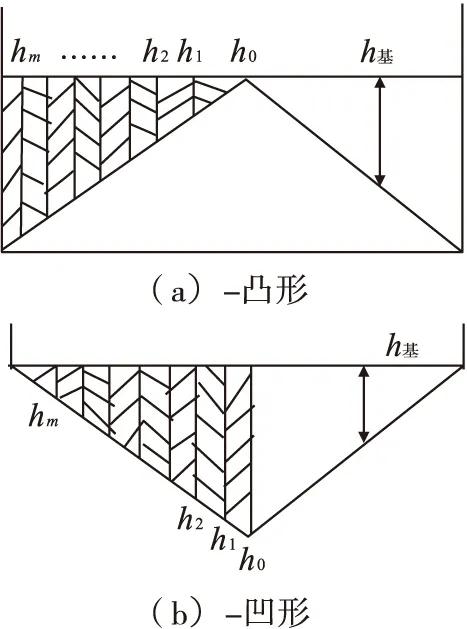
图3 各圆环体积
根据图3所示,各阴影部分体积(即各圆环对应的容量)由内向外分别为:

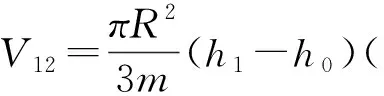
式中罐底如图3(a)V11为0,如图3(b)V12为0。


……
以上各项相加得罐底量容积[5]:

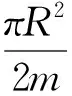

(2)
对于任一编表高度hd(相对于下计量基准点高度)对应罐底交点d,如图4所示,d点相对于罐底最低点高度为hd+h基,其相对于同心圆测量点hm高度为:
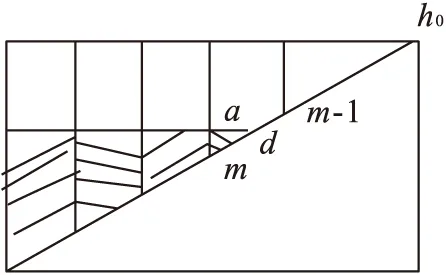
图4 任一点对应容积局部示意图
h=hd+h基-hm
(3)
将h基-hm=Bm-B基代入(3)式 得h=hd+Bm-B基
从图4可以看出:当hd+Bm-B基>0时,Bm对应的罐底点在d点之下,其对应的圆环阴影部分体积是高度hd编表的一部分;当hd+Bm-B基≤0时,Bm对应的罐底点在d点之上,其对应的圆环阴影部分体积不是hd高度编表的一部分剔除。设自定义函数:
把自定义函数和同心圆个测量点算术平均值公式代入(2)式可得规程中的公式:
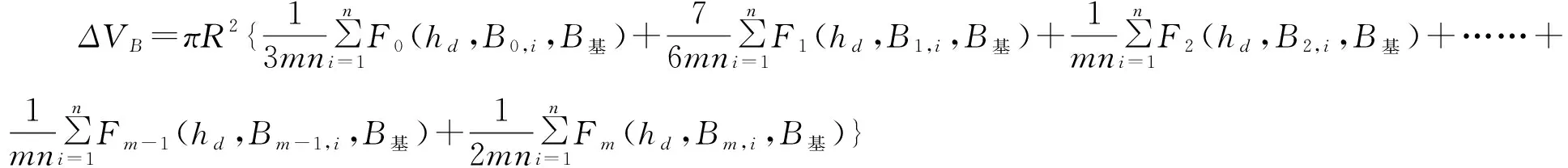
(4)
其中:
ΔVB为罐底容量,高度hd的函数;
hd为编制底量表液位高度(区间为下计量基准点至罐底最高点);
R为罐基圆半径;
B0,iB1,i…Bm,i为各测量点标高;
B基为下计量基准点标高;
F(hd,Bm,n,B基) 为自定义函数;
Fm(hd,Bm,i,B基)=

当m=1时用下式计算:
(5)
3 算法分析及改进
3.1 算法分析


根据自定义函数的定义,公式(5)的函数条件语句B0,i+hd≤B基则其第一项为0,公式(5)可简化为:
利用公式(6)计算得底量数据如表2所示。
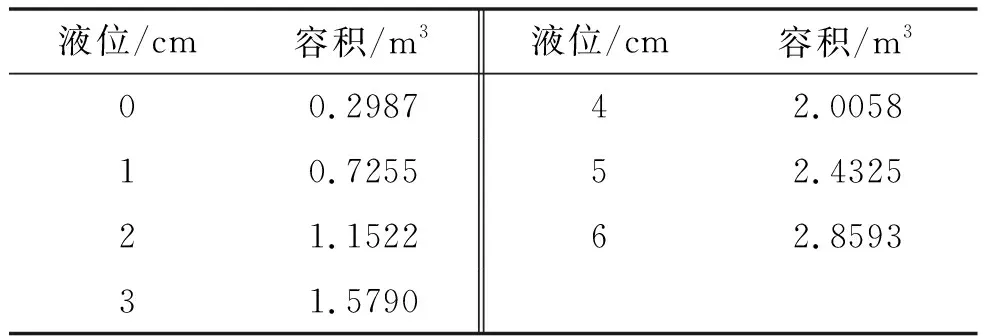
表2 底量计算结果表
对照表1和表2数据可以看出,表2计算的数据在同心圆之间时数据存在较大的偏差。
3.2 算法的改进
3.2.1 自定义函数中变量的修改
公式(4)的自定义函数测量点标高Bm,i,m作为变量使用容易产生概念混淆,对于任一确定的被测量罐其对应的等分圆个数为定值即m是常量。这里把测量点标高定义为Bj,i(j=1…m,i=1…n)。
3.2.2 算法的改进
通过上面分析验证发现,编表高度hd在同心圆周上时,这时公式(4)的计算结果正确,当hd在j和j-1圆环之间时如图5所示,其体积是使用πR2/m采用比例内插求得(在图5是Sa+Sb对应的体积)而非线段a所对应的圆环体积(Sa)。下面修改公式(4)的自定义函数来对这部分体积进行修正。
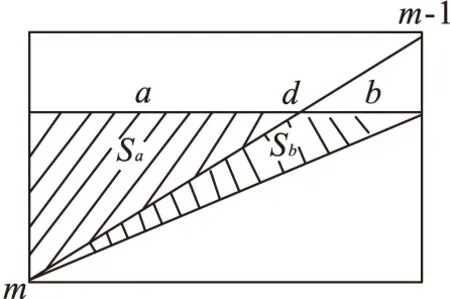
图5 局部容积放大示意图
当测量点圆环个数m>1且hd不在第一圆环上时,相邻两圆环周长可以认为近似相等设为L,由图5两相似三角形可得:

a线段对应的圆环面积为S=aL。
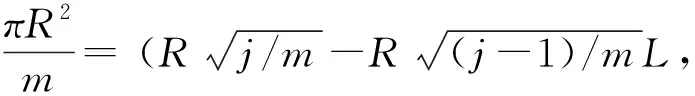
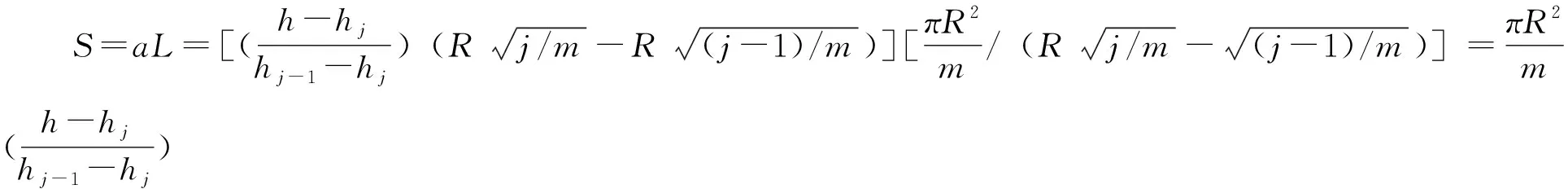
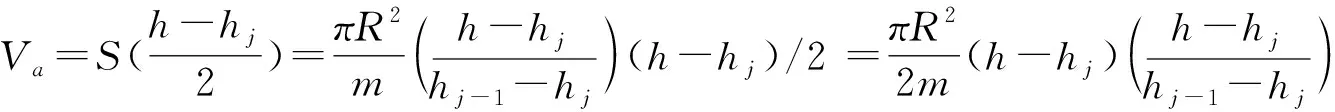
由公式(3)可知h=hd+Bj-B基hj-1-hj=Bj-Bj-1代入上式得:
重新定义自定义函数:
从函数的定义可看出ΔVB是从j+1圆周开始计算容积的设为VB,漏掉了一部分容积,设这部分容积为Vx,则罐底容量为:ΔVB=VB+Vx。其中Vx的取值如下:
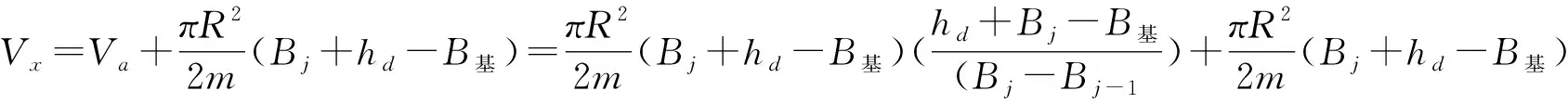


当m=1时加上求和公式可用下面公式计算:
利用上式计算结果如表3所示。
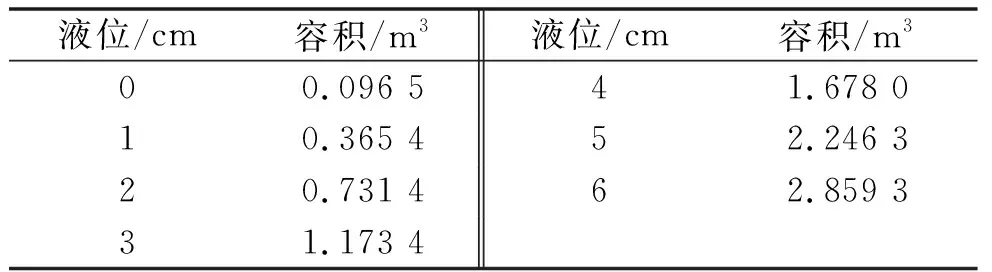
表3 底量计算结果表
对比表1、表2和表3的计算数据可看出,经过修正后的表3的计算数据更接近表1的计算数据(真值),达到了修改的目的。上面对修改后公式的验证虽然是采用m=1特例来验证的,但修正公式是按照一般性通用公式来推导的,适用于任何锥形底(或类锥形底)罐底量的计算。
4 结束语
通过储罐检定几何法计算公式的分析推演,找出计算结果存在偏差的原因,并对该算法计算结果局部存在偏差的问题给出修正方法。通过修正数据偏差提高了底量表的准确度,使计算结果更加准确与合理。虽然计算过程有点繁琐,但利用计算机编程很容易实现。
