计及绞线表面粗糙度的大风区接触网正馈线舞动响应研究

2021-10-18张友鹏岳永文赵珊鹏王思华

铁道科学与工程学报 2021年7期

张友鹏，岳永文，赵珊鹏,2，王思华

(1.兰州交通大学自动化与电气工程学院，甘肃兰州730070；2.兰州交通大学甘肃省轨道交通电气自动化工程实验室，甘肃兰州730070)

兰新高铁全长1 775.779 km，是目前高海拔地区运营里程最长的高速铁路。线路全程途经甘肃境内的安西风区和新疆境内的烟墩风区、百里风区、三十里风区、达坂城风区五大风区的总长度达579.599 km，占线路总长的32.6%，其中举世闻名的百里风区、三十里风区是世界内陆风力最为强劲的地区。大风具有风速高、风期长、风向稳定、起风快的特点，近年来多次威胁兰新铁路的行车安全并造成列车倾覆等重大安全事故[1−3]。为保证列车安全运行，风区沿线修建了挡风墙防风工程[4]，从而避免了列车发生倾覆事故，兰新高铁挡风墙及接触网结构如图1所示。

图1 兰新高铁挡风墙及接触网结构示意图Fig.1 Schematic diagram of Lanzhou-Urumqi high-speed railway catenary and wind-break wall

由于正馈线通过V型悬挂的绝缘子与接触线同杆架设于支柱外侧且没有任何补偿装置[5]。百里风区大风从铁路侧面垂直吹向线路，因此极易造成运行中的接触网正馈线发生风致舞动，现场观测到的舞动现象如图2所示。挡风墙的设置虽然可以防止列车倾翻，但是却加剧了正馈线的舞动，从而引发接地短路、金具磨损、疲劳断线等事故发生，严重影响正馈线的稳定运行，对铁路运输安全构成威胁。

图2 百里风区兰新高铁接触网正馈线舞动Fig.2 Catenary positive feeder galloping of Lanzhou-Urumqi high-speed railway in Baili gale area

国内外学者针对导线舞动现象的研究主要集中在覆冰输电导线的舞动，对于兰新高铁接触网正馈线舞动的研究较少。DEN HARTOG[6]针对覆冰输电导线舞动，提出垂直舞动激发机理。NIGOL等[7-8]在垂直激发机理的基础上，提出扭转舞动激发机理，提出了导线系统的3自由度运动方程。然而，导线在薄覆冰(不足以形成非对称截面)及无覆冰状况下也会发生舞动现象，刘亮等[9]提出了关于薄(无)覆冰导线舞动的参数共振机理并进行了相应的试验验证。雷娟棉等[10]采用Transition SST模型对不同高雷诺数的圆柱绕流问题进行了数值模拟，对圆柱表面的流场分离进行了研究，但是没有考虑粗糙度对圆柱表面流场分离产生的影响。与输电线舞动相比，电气化铁路接触网正馈线舞动的研究相对较少。张友鹏等[11]研究了兰新高铁接触网正馈线的气动特性，分析了不同尺寸挡风墙对正馈线气动特性的影响，在研究中并未考虑正馈线表面粗糙度对导线气动特性的影响。王玉环[12]对大风区接触网正馈线的同阶共振频率进行了分析，通过大量观测数据得到了正馈线舞动轨迹，并提出了正馈线张力补偿方案，以改变风场与正馈线频率，从而达到正馈线防舞的作用；韩佳栋[13]对附加导线舞动的风速频域、尾流驰振进行了分析，并提出了相关防舞措施，但未对其机理进行研究。RELF等[14]在英国国家实验室，对多绞线和光滑圆柱进行了相应试验，验证了绞线表面粗糙度对阻力系数的影响。现有关于接触网正馈线气动特性和舞动响应的研究，均是将正馈线简化为光滑圆柱，忽略了绞线表面粗糙度对其气动特性及舞动响应的影响。本文针对大风环境下兰新高铁接触网正馈线的舞动，结合结构动力学方法建立正馈线力学模型并进行舞动方程推导。建立考虑正馈线表面粗糙度的仿真模型，对计算域进行网格划分，通过流体力学数值计算的方法研究正馈线气动特性，分析绞线表面粗糙度对正馈线表面流场分布情况及升、阻力系数的影响。结合正馈线的舞动方程及所受风荷载，求解不同风速下的正馈线舞动响应，分析有墙环境下表面粗糙度对正馈线舞动时程响应的影响。研究结果可以为更加深入地研究正馈线舞动机理及探明表面粗糙度对导线气动特性的影响提供理论支撑。

1 正馈线舞动微分方程解析

本文根据结构动力学中梁的振动弯曲理论，将正馈线视为梁的弯曲问题处理，考虑接触网正馈线舞动过程中自身的阻尼力，在正馈线上取一长度dx的微元段，受力分析如图3所示。

图3 正馈线微分段舞动力学模型Fig.3 Positive feeder micro-segment vibration mechanical model

在分析正馈线舞动时，可以将正馈线简化为欧拉−伯努利梁[15]。分析推导正馈线在水平与垂直方向发生舞动时的舞动微分方程。

在稳定的风荷载作用下，正馈线微元段的平衡方程如式(1)。

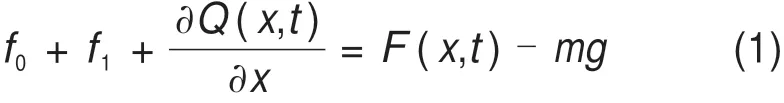
式中：f0为正馈线发生舞动时自身所具有的阻尼力为单位长度质量；c为正馈线质量比例阻尼；Q为微元段两端的剪力；F(x,t)为正馈线所受风荷载。

根据力矩平衡方程，有

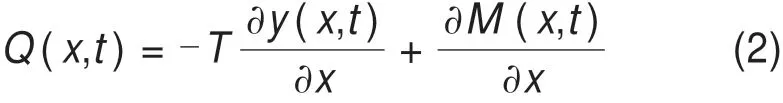
将式(2)代入式(1)中，有

根据欧拉−伯努利平截面的假设，有

将式(4)代入式(3)中，得到正馈线的运动方程如下：

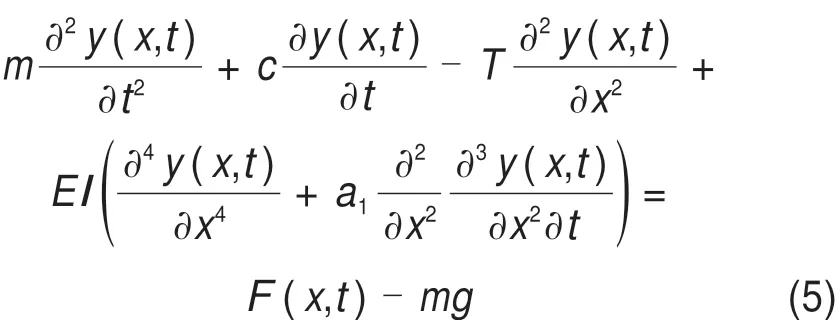
式中：y(x,t)为正馈线的舞动位移；T为正馈线的水平张力；EI为正馈线有效抗弯刚度；a1为刚度比例阻尼。正馈线自身阻尼由质量比例阻尼和刚度比例阻尼组成，这2种阻尼合称Rayleigh阻尼。正馈线发生舞动时，质量比例阻尼的影响远大于刚度比例阻尼[16]。在计算正馈线的舞动时，忽略刚度比例阻尼的影响，则正馈线在风荷载下舞动方程简化为：

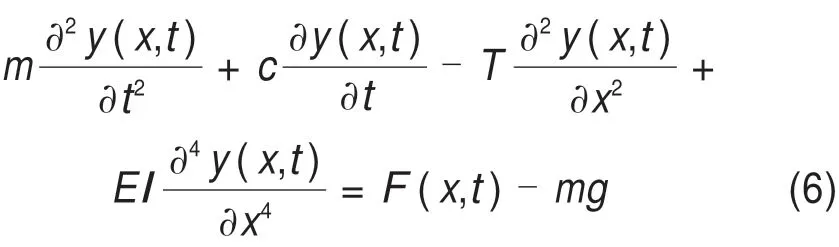
式(6)对应的齐次微分方程为：

令y(x,t)=f(x)g(t)，其中f(x)，g(t)分别是关于x和t函数，代入式(7)并利用分离变量方法求得：

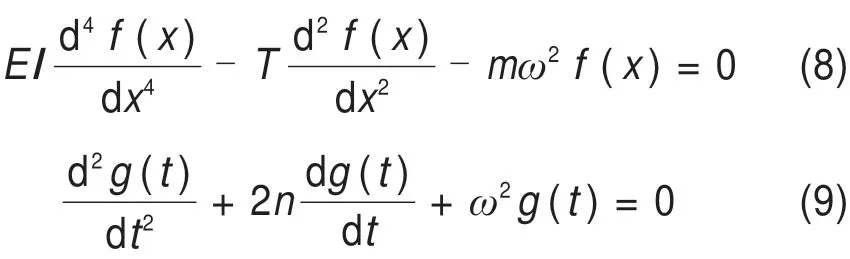
式中：n=c/2m。

式(8)的解为：

式中：

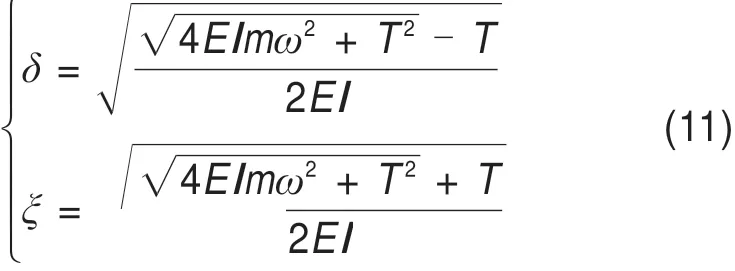
根据边界条件f(0)=f″(0)=f(L)=f″(L)=0，可求得：C1=C3=C4=0。

由f(L)=0，有

可得

将式(13)代入式(11)可得：

将式(13)代入式(10)中，可得：

式(14)、式(15)分别为式(7)的特征值和特征向量组。故式(6)的解为：

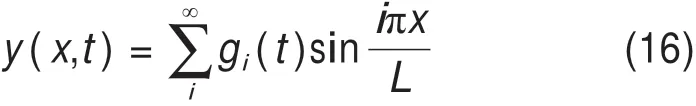
式中：gi(t)为关于时间t待求量。将式(16)代入式(6)，利用特征向量的正交性可求出正馈线的舞动微分方程。因兰新高铁接触网跨距相对较小(30-55 m)，现场观测到正馈线只发生一阶舞动，故需求解正馈线的一阶舞动微分方程：

2 模型建立及计算分析

2.1 物理模型及控制方程

以兰新高铁接触网正馈线为研究对象，现场架设的钢芯铝绞线实物及其截面结构如图4所示。

在黏性流体力学中，流体的运动规律可用NS方程进行描述，其在惯性直角坐标系下的连续性方程以及动量方程可表示为：

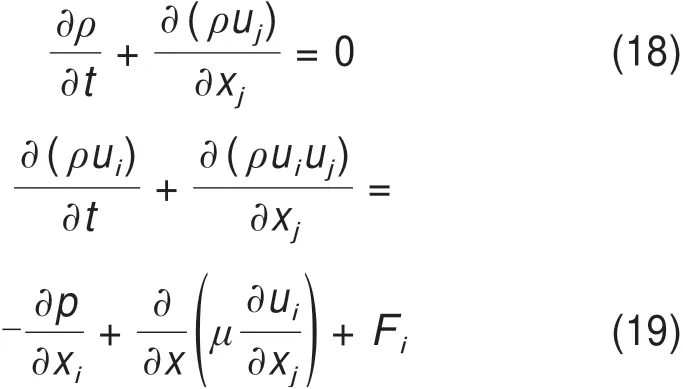
式中：ρ为流体密度；t为流动时间；i,j=1,2,3；μ为流体的动力黏性系数；Fi为流体微元体上的i方向的力。

正馈线的升、阻力系数及St和Re数定义如式(20)：

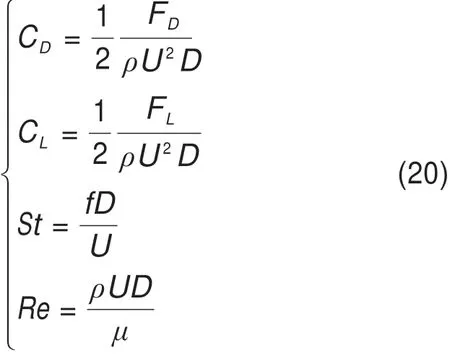
式中：FD和FL为导线所受气动升力和阻力；ρ为空气密度；U为入口风速；D为正馈线外围直径；f为旋涡脱落频率；μ为流体动力黏度。

2.2 计算域及边界条件

本文以现场实际尺寸设置计算域，挡风墙高度为3.5 m，计算域为23.8 m×15 m。计算过程中，流体计算域是CFD数值计算的载体，网格的质量直接影响整体计算的效率及精确性。为保证网格高度的独立性，采用低雷诺数网格划分方法。对于大多数求解器，充分利用低雷诺数的边界特性，通常认为网格第一层高度必须达到与y+<1相等的高度。低雷诺数下为确定在相应的约束范围内划分网格，使用基于平板理论的经验公式计算第一层网格高度，计算公式为[17]：

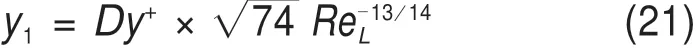
式中：y+为首层节点到无滑移壁面的无量纲距离；D为导线外围直径；ReL为低雷诺数。

在Re较大(风速较大)时，对近壁面网格要求极高，壁面网格的法向增长率取1.05，确保边界层中至少有5个网格单元，壁面网格周向宽度与径向高度y1的长宽比保持在20:1以下。流体计算的整体网格，如图5所示；光滑表面和粗糙表面的近壁面网格，如图6所示。

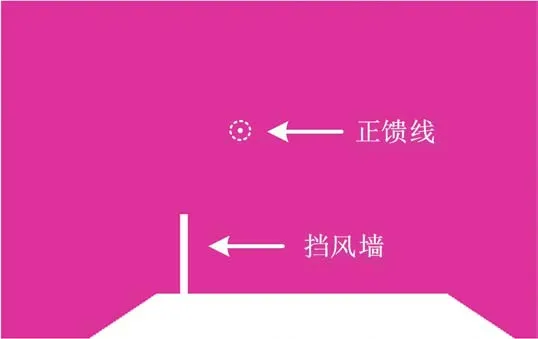
图5 流体计算域网格示意图Fig.5 Schematic grids of computational domain

图6 正馈线近壁面网格示意图Fig.6 Local grid refinement of smooth section and real rough section of positive feeder

相对于常规的圆柱绕流，本文模型中的挡风墙对正馈线周围的气流产生一定的增速加压作用，而Transition SST模型对气流流动分离及压力梯度等因素较为敏感，可以很好地模拟正馈线表面的压力变化及高雷诺数的圆柱绕流问题，所得结果与试验结果更为接近。计算域边界条件设置：气流从左向右垂直进入流场，左侧边界为速度入口边界。导线表面采用无滑移壁面边界，右侧边界为压力出口边界。速度压力耦合采用SIMPLEC算法，压力方程用二阶离散精度，动量用二阶迎风模式，计算时间步长取0.01 s，设置不同流速进行仿真。

在计算过程中不可忽略挡风墙对气流汇聚加速作用及对正馈线周围气流产生的影响，同时气流经过挡风墙会在其后方产生不规则的大涡流也会对导线周围流场产生影响，如图7所示。

图7 气流经过挡风墙后流场图Fig.7 Flow field diagram after the airflow passes through the wind-break wall

2.3 计算结果分析

根据兰新高铁大风区段沿线常年所处的风速范围，本文针对1～30 m/s(1～11级)风速进行了仿真计算。图8为入口风速为15 m/s，光滑表面和粗糙表面的正馈线1～4 s流场分布图，由图8可知，在光滑表面正馈线后方会产生较大的漩涡，从而产生更大的气流扰动作用；而且在粗糙表面上容易出现气流提前分离的现象，这与光滑表面有很大的差异。

图8 风速15 m/s时不同表面正馈线流场图Fig.8 Flow fielddiagram of positive feeders on different surfaces at 15 m/s wind speed

图9 为入口风速15 m/s时，2种不同表面正馈线壁面速度云图及尾部速度云图。由图9可知，光滑表面流场风速大于粗糙表面流场风速，光滑表面尾部的漩涡容易脱落，壁面不会产生细小漩涡；而粗糙表面尾部的漩涡不会在短时间脱落，并在表面凹陷的部分会产生细小的漩涡，这表明表面粗糙度会影响正馈线周围流场的分布情况。

图9 风速15 m/s时不同表面正馈线速度云图Fig.9 Flow field at the tail of 15 m/s conductor model with different cross section

风速为15 m/s时，2种表面正馈线模型升、阻力系数时程图，如图10～11所示。

通过对比图10与图11的升、阻力系数时程曲线可知，表面粗糙对正馈线升、阻力系数有很大的影响。同一风速下考虑绞线表面粗糙度，正馈线升、阻力系数明显小于光滑表面正馈线的升、阻力系数，表1为光滑表面和粗糙表面正馈线模型，在不同风速下正馈线升、阻力系数均方根值。

图10 风速15 m/s时光滑表面正馈线升、阻力系数时程图Fig.10 Time history diagram of lift and drag coefficient of positive feeder with smooth surface at 15m/s wind speed

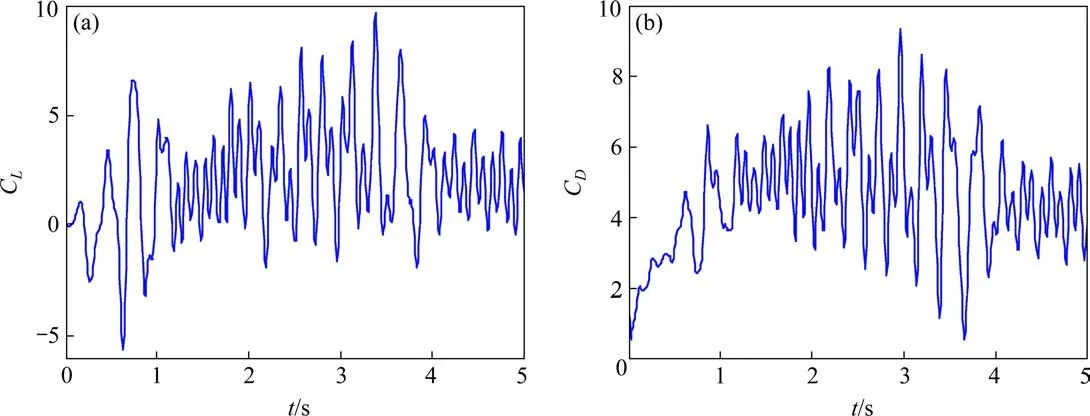
图11 风速15 m/s时粗糙截面正馈线升、阻力系数时程图Fig.11 Time history diagram of lift and drag coefficient of positive feeder with rough surface 15 m/s wind speed

利用表1绘制光滑表面和粗糙表面正馈线模型升、阻力系数在不同风速下的曲线，如图12所示。风速为1 m/s时，2种模型的升、阻力系数大致相同，这表明低风速环境下，雷诺数较小时，正馈线表面粗糙度对升、阻力系数基本无影响。但在风速较大时，考虑导线表面粗糙度，正馈线的气动系数会明显降低，这与RELF等的研究结果相同[14]，验证了本文仿真的正确性。故在雷诺数较大情况下，忽略正馈线的表面粗糙度会导致正馈线的气动升、阻力系数的计算结果产生偏差，为了准确表征高风速下正馈线气动特性，应考虑正馈线的表面粗糙度。

表1 不同风速下2种表面正馈线模型升、阻力系数Table 1 Lift and drag coefficients of two kinds of surface positive feeders at different wind speeds

图12 不同风速下2种表面正馈线升、阻力系数曲线Fig.12 Curves oflift and drag coefficients of two kinds of surface positive feeders at different wind speeds

3 接触网正馈线舞动响应分析

本文以兰新高铁现场运营接触网正馈线为算例，相关参数如表2所示。

表2 兰新高铁接触网正馈线基本参数Table 2 Basic parameters of Lanzhou-Urumqi high-speed railway catenary positive feeder

结合接触网正馈线的舞动微分方程式(17)，在不同风速下，对风荷载环境下接触网正馈线进行受力分析，如图13所示。

图13 风荷载下正馈线受力示意图Fig.13 Schematic diagram of the force of positive feeder

在风轴坐标系下，作用在正馈线上的气动阻力FD和升力FL如下：

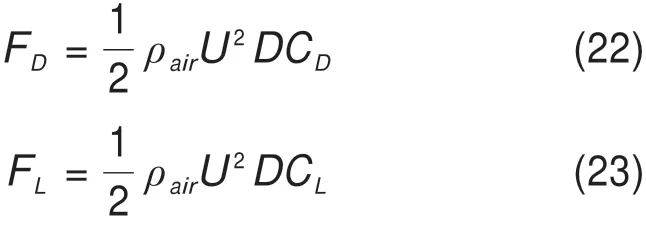
式中：ρair为空气密度；D为正馈线外围直径；CL，CD为升力、阻力系数。

在挡风墙影响下，不同风速下正馈线位置处风攻角会发生变化，如图14所示。从图14中可以看出，正馈线风攻角随风速的增大逐渐变大，当风速增大到15 m/s时风攻角稳定在30°左右[11]。

图14 风攻角α随风速变化示意图Fig.14 Schematic diagram of wind attack angle α changing with wind speed

作用在正馈线上的风荷载会随风攻角的变化发生变化，根据图13风荷载下正馈线的受力分析及图14不同风速下对应的正馈线风攻角，可得到正馈线在不同风速下所受风荷载的水平分量FX和垂直分量FY，如下：

结合正馈线舞动微分方程式(17)可以求出正馈线在不同风荷载下的舞动时程响应。选取正馈线跨中特征点作为研究对象，分析光滑表面与粗糙表面正馈线的舞动时程响应。图15分别为风速10 m/s和20 m/s时2种表面正馈线模型跨中特征点水平与垂直舞动时程响应。

从图15中的2种不同表面模型在不同风速下的舞动时程响应曲线可知，在考虑正馈线表面粗糙度的条件下，正馈线的迎风特性发生了变化。在相同风速下，光滑表面模型的水平、垂直舞动幅值大于粗糙表面模型的水平、垂直舞动幅值，且2种模型的垂直舞动幅值均大于水平舞动幅值。这表明大风环境下考虑导线表面粗糙度，正馈线水平、垂直舞动幅值相对减小，更贴合现场实际舞动状态。