地铁车辆底架薄壁梁吸能结构耐撞性试验与仿真研究

刘莉，高宁，许喆，高峰，张相宁，李佳霖，冯推银，于尧，高广军

(1.中车唐山机车车辆有限公司 技术研究中心，河北 唐山063035；2.中南大学 交通运输工程学院 轨道交通安全教育部重点实验室，湖南 长沙410075)

碰撞事故是汽车、船舶、火车等运输工具都需要共同预防的事故类型，各类运输工具的碰撞安全性课题一直以来都是社会关注的焦点，也一直是学者的研究热点[1]。尽管现代轨道车辆安全保障技术已经有了很大提升，但碰撞事故仍然无法完全避免，近年来，轨道车辆碰撞事故在世界各国时有发生[2]。根据历年来世界铁路事故统计数据，造成重大人员伤亡的事故中，由于列车碰撞所造成的事故所占比例高达56%。城轨列车碰撞被动安全防护技术中重要部分是设计一款适应车体结构的吸能结构，在发生碰撞事故时，吸能结构会通过塑性变形吸收碰撞所产生的能量[3]。研发和改良列车吸能结构，对提高轨道车辆碰撞安全性有着重要的作用。轨道车辆吸能结构可以大致分为2种类型，一种为底架薄壁梁吸能结构，在未发生碰撞事故时，该类结构能够作为底架承载结构承担车体重量，传递纵向力；发生碰撞事故时，能够有效耗散由于碰撞产生的能量[4]。第2种类型为附加式吸能结构，该类结构安置在车体端部，发生碰撞时，该种吸能结构通过有序压溃变形来吸收碰撞能量[5]。金属薄壁结构广泛应用于吸能结构中，该类结构有多种类型，如圆管、方管、多边形管、填充蜂窝铝或泡沫铝的薄壁结构，对应的吸能模式也各不相同，如压溃、膨胀、缩颈、翻转、撕裂以及各种组合式等[6−8]。SUN等[9]提出了一种蜂窝压溃式吸能结构，并通过实验手段验证了该结构有效性。LI等10]研究了一种收缩式吸能结构，在收缩套的约束下，圆管产生径向收缩塑性变形，吸收冲击动能。GUAN等[11]提出了一种切削式吸能结构，金属材料在切具的作用下，发生断裂吸收冲击动能。除此之外，LIU等[12]提出了一种钢板弯曲式吸能结构，该结构利用金属薄板在冲压过程中发生弯曲−拉直的塑性变形，不断吸收冲击动能，并通过实验验证了结构的稳定性。以上吸能结构均可作为附加式吸能结构安装在列车端部，对于安装空间要求较高。对于城轨车辆来说，该类车型端部空间狭小，且由于车钩安装座的限制，极大的制约了附加式吸能结构有效变形空间，从而造成城轨车辆耐撞性能不符合要求。对于上述情况，采用底架薄壁梁吸能结构可有效解决以上难题。XU等[13]针对于底架式薄壁梁吸能结构，提出了一种渐进梯度式底架吸能结构，结构在碰撞过程中实现逐级屈曲吸能，并通过方针和实验手段，对结构进行了优化设计。在城轨车辆的吸能结构设计中，一般将载客区域结构的承载能力设计高于车体端部可变形区域，目的是为了确保在碰撞过程中塑性变形仅局限于预先设定的可控变形区内。同时，在车辆端部可变形区域前部安装防爬装置，可抑制列车出现爬车情况，使吸能结构能够更充分的发生塑性变形。车体能量吸收结构的设计通常采用压溃式吸能结构。本文根据城轨车辆的结构形式，将设计约束定位典型地铁头车车体司机室安装接口，设计了一种司机室底架式薄壁吸能结构，在列车正常运行中起承载作用，在发生碰撞时，吸能结构产生塑性变形耗散冲击动能。本文的承载式吸能结构采用了带隔板薄壁管结构，研究了此类司机室承载式吸能结构的耐撞性能。第1部分提出了司机室底架承载式薄壁吸能结构的几何模型和本构模型，并给出了模型各个组成部分的设计参数与连接方式；第2部分对薄壁吸能结构进行了动态冲击试验，研究了该种结构的耐撞性能；第3部分对吸能结构的有限元模型以及耐撞性试验结果进行了对比分析，并根据结论给出建设性意见。

1 结构几何模型

图1 为本文设计的城轨车辆底架承载吸能结构，其主体结构主要分为5部分：1—司机室骨架；2—支撑梁；3—边梁；4—吸能结构；5—防爬齿结构。司机室的骨架结构由材料为铝合金梁构成。边梁结构由材料为铝合金薄壁铝板材弯曲而成，截面厚度为6 mm，尺寸为108 mm*165 mm。在结构端部设置防爬齿，防爬齿结构如图2所示，结构的材料为铝合金，尺寸为170 mm×1 000 mm×40 mm。本文的防爬齿设计成左右两端错开分布态势，右侧上下两端分别设置防爬齿，左侧中间一端设置防爬齿，防爬齿结构通过螺栓连接或者焊接与底架前端盾体进行连接。可同时起到自动对心、上下防爬、左右防偏的作用[14]。

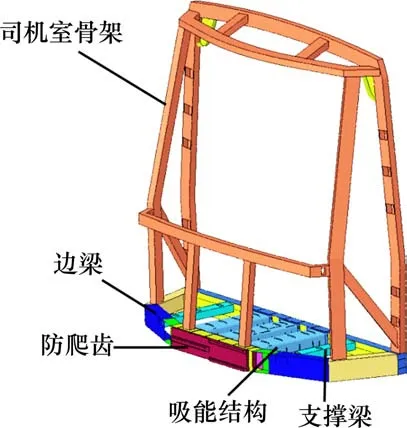
图1 吸能装置示意图Fig.1 Scheme of the energy absorber

图2 防爬结构Fig.2 Scheme of Anti-climb structure

薄壁梁吸能结构能够通过不同类型的薄壁管梁结构排列组合设计，成为一种拥有优良耐撞性能的承载式吸能结构。本文底架中间区域均匀分布了3个吸能结构，总的结构长度为650 mm。吸能结构主要由4部分组成：薄壁方管、隔板、端板以及诱导结构。其中薄壁方管通过2块对称的U型板结构焊接相连，厚度设为3 mm，4个倒角半径为15 mm，整体长度为650 mm，前端端面截面尺寸为200 mm*150 mm，隔板厚度为3 mm。为了方便能够与隔板焊接，在方管四面均开有长条孔，长度为对应方管截面边长的1/2。方管两端焊接有2块厚度为10 mm的端板。方管的内部安装了十字形隔板，主要目的是约束方管的屈曲变形以及加强吸能结构刚度，从而吸收更多的冲击动能。

渐进变形模式是吸能结构最理想的变形模式，碰撞发生后结构首先在冲击端附近产生褶皱，在相邻隔板之间会发生屈曲褶皱，并随着碰撞的进行沿途的管壁依次发生变形，直至能量耗散完毕或结构被完全压实。在碰撞初期，为了诱导吸能结构能够有序变形，在薄壁方管外侧设计了诱导结构，如图3所示。在方管非焊接面引入一个长度为150 mm，宽度为20 mm，深度为5 mm的凹形冲压槽，以降低该面的初始强度。在碰撞发生时，通过凹形区域率先变形，并诱导整个结构发生有序的屈曲变形。前部端梁内部设置有纵向支撑板，以增强端部受冲击区域结构强度，如图3所示。

图3 吸能结构内部组成Fig.3 Internal composition of energy absorbing structure

2 结构冲击实验

为了验证所本文设计的城轨列车承载式司机室结构变形的稳定性和协调性，以及城轨列车端部吸能结构耐撞性是否满足设计要求，在中南大学高速列车研究中心碰撞台对该结构进行了台车冲击试验。冲击试验撞击的工况设定为配重台车在空气炮驱动下，以6.5 m/s的速度撞击静止刚性墙，试验整体有限元模型和实物如图4所示。通过冲击试验，得到了该结构碰撞动态响应的数据。通过端板螺栓连接将司机室组件固定于试验台车端部。具体试验工况如下：台车与吸能结构总质量为27 t。以预定速度等级进行碰撞试验，测试数据为：速度、加速度、变形量、吸能量和变形模式等。

试验台车整体的有限元模型和实物三视图如图4。

表1 碰撞试验工况Table 1 Impact test conditions

图4 试验台车整体有限元模型Fig.4 Test the overall finite element model

在完成试验后，对试件位移随时间、撞击力随时间的变化规律、能量耗散情况以及变形破坏情况进行了详细的对比分析。在本次试验中，运用了2台高速摄影设备分别从侧面和顶部对试件撞击刚性墙的过程进行了拍摄。吸能结构是否产生稳定有序变形是结构耐撞性的一项重要评价指标。高速摄影以拍摄频率为3 000帧/s的超高帧速率捕捉吸能结构变形模式，所拍摄的吸能结构俯视和侧视变形结果如图5所示。

图5 整体实物图Fig.5 Overall physical map

从图5中可以看出，司机室在撞击刚性墙的一瞬间，屈曲变形率先在吸能结构诱导槽附近产生，如图所示，随着司机室撞击的不断进行，吸能结构随之产生有序稳定的屈曲变形，随后司机室骨架前端梁与刚性墙接触，向下产生折弯，当撞击进行得更深入时，司机室的骨架竖梁与刚性墙接触，此时司机室U型斜撑梁强度较弱率先发生扭转，保障了司机室骨架在不发生失稳的前提下整体向后移。随着撞击的继续，运动台车动能逐渐被吸收，撞击速度逐步降为0，撞击结束。之后由于碰撞压缩产生试件弹性势能进行释放，台车产生了一定程度的回退。底架整体结构屈曲变形率也先在诱导槽附近产生，并以远离撞击端方向依次发生渐进屈曲，整个变形模式与设计变形一致。结构整体保持了较好的稳定性，没有发生失稳的情况，边梁结构的弯曲变形没有产生明显撕裂。带隔板薄壁方管结构一共产生了4级屈曲褶皱，褶皱的位置均产生在相邻隔板之间，并产生了有序稳定的压溃变形。

由于城轨列车司机室撞击面的尺寸过大，无法直接通过布置测力面板获得撞击力，因此本文通过在台车上加装了加速度传感器，撞击力-位移曲线可以通过加速度曲线积分拟合得到，如图6所示。由于在撞击过程中，加速度传感器受到台车结构振动影响较大，导致加速度曲线波动较大，因此拟合得到的撞击力曲线也较为明显。同时由于加速度传感器触发过程中有一定的滞后性，因此在撞击初期，加速度并未产生明显的峰值力，导致积分后得到的撞击力在撞击初期未出现峰值。通过观察，能够明显的看到4个大的波峰，撞击过程平均撞击力为1 448 kN，最大峰值力约为2 007 kN。所吸收的能量为撞击力曲线与横坐标轴围成区域的面积，可得出结构吸能量为538 kJ。

图6 撞击力−时间及吸能量−位移曲线Fig.6 Impact force-time and energy absorption-displacement curve

3 有限元模型

本文的数值仿真采用的是显式动力有限元AN‐SYS/LS-DYNA，所设计有限元模型的准确性，对分析结果的精度有着决定性作用，故需要建立一个有效性可靠的有限元模型。

Lagrangian算法是最通用的显示有限元，适用于计算连续质量单元的运动[15]。在显式有限元算法中假设当前时步为第n步，有如下运动方程：

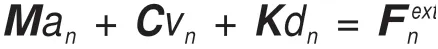
式中：M为结构的质量矩阵；C为结构的阻尼矩阵；K为结构的刚度矩阵；Fextn为外界作用力矢量；an为时步n时的加速度；vn为时步n时的速度；dn为时步n时的位移；上述方程可被改写成Man=内部作用力(如：沙漏力)矢量。在时域应用中心差分法得：

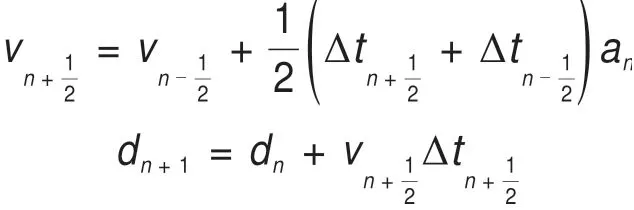
因此在整个时域范围内，可由上述积分递推公式求得各个离散时间点处的位移速度和加速度这种求解过程被称为显式积分算法。在对城轨列车防撞击司机室有限元碰撞分析时，按照1:1建立撞击模型。碰撞过程中，轨道由于台车的限制仅可以沿轴向运动，对应的，在有限元仿真中约束台车底部车轮的自由度，使系统仅能沿轴向运动，司机室通过焊点连接方式安装在台车前端。台车的尺寸设置为长10 m，宽3.3 m，高4.3 m，台车有限元模型如图7所示。

台车结构采用四节点薄壳单元进行网格划分，鉴于台车结构不参与吸能，为了减少计算时间，将台车模型网格离散得相对较稀疏，网格单元尺寸为120 mm×120 mm。刚性墙的尺寸为宽5 m，高5.5 m，厚300 mm，采用八节点实体网格进行划分，网格大小为100 mm×100 mm×100 mm。墙上装有一对防爬齿，各参数与司机室防爬齿一致。底架也是采用壳单元进行模拟。由于薄壁方管作为主吸能结构，此处的网格离散应相对较密集，网格单元尺寸为4 mm，底架边梁结构单元尺寸为8 mm，图7为车体底架承载式吸能结构有限元模型。有限元模型的接触类型均采用自动单面接触(Contact_Automatic_single_surface)算法来进行模拟分析，设置动摩擦因数为0.1，静摩擦因数为0.5。根据司机室所采用的模型，该模型的屈服应力可由下面公式得到：

图7 台车有限元模型Fig.7 Trolley finite element model

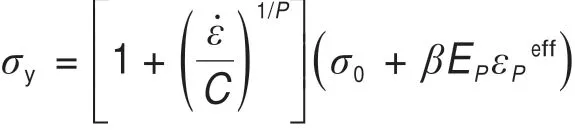
式中：σ0表示初始屈服应力；ε̇表示应变率；C，p表示应变率参数；表示有效塑性应变；Ep=其中：E为弹性模量，Et为塑性变形切线模量，β是硬化系数(β=1硬化为各向同性，β=0硬化为随动硬化)，本文选用β=0.3。在冲击过程中，薄壁管梁结构屈曲变形过程既涉及到了材料的压缩又涉及到了材料的拉伸。在材料试验中，一般对于塑性好的材料要用拉伸判断，对于脆性大的材料最好用压缩试验来测量，相比压缩试验，材料拉伸试验对仪器精度要求低、试验简单。对于不锈钢材料以及5系铝合金材料均属于塑性良好材料，在拉伸试验过程中，可更好地记录应力-应变曲线。为了获取应力应变曲线，参照《GB 228—2002金属室温拉伸实验标准》对5083铝合金以及304不锈钢材料进行材料拉伸试验，材料拉伸试验场景以及2种材料真实应力应变曲线如图8所示，其中材料拉伸试验机拉伸速度为1 mm/min，引伸计标距为100 mm。

图8 材料拉伸试验Fig.8 Material tensile test

仿真工况为一辆前端装本文所设计城轨列车防撞击司机室的台车以6.5 m/s的速度撞击刚性墙。吸能结构为不锈钢薄壁方管，台车与司机室总质量为27.7 t。司机室整体有限元仿真变形序列应力云图如图9所示。

图9 撞击力−时间曲线Fig.9 Impact force-time curve

通过图6撞击力—时间曲线可以看出，最大峰值力为1 973 kN，出现的时间为试件与刚性墙刚接触发生刚性碰撞的时刻。从曲线可以看出，除了撞击峰值力之外，撞击力基本上都以1 450 kN为均值在上下波动，曲线上一共产生了4个屈曲褶皱，每一个完整波峰波谷都对应着薄壁方管的一次屈曲变形。撞击初期，由于台车速度较快，结构的变形也较为迅速，撞击力起伏变化明显。随着撞击的进行，由于吸能结构发生塑性变形，冲击动能逐渐被耗散，结构变形与撞击力也逐渐变缓和。主吸能结构是司机室前端的带隔板薄壁方管，薄壁方管有限元模型仿真变形序列应力云图如图10所示。该结构的吸能量大小直接决定了整个底架承载式吸能结构的吸能能力。薄壁方管的屈曲变形模式是材料与结构选取的首要考虑因素之一。通过观察可以发现，在撞击过程中屈曲变形率先在诱导槽附近产生，并以远离撞击端方向依次发生渐进屈曲，变形过程与预期变形一致。结构整体未出现失稳的情况，并且屈曲变形较为规整，吸能结构均产生了对称的变形模式，整个碰撞过程发生四级完整屈曲变形，通过分析最终分仿真结果可得：结构整体最终变形量为408.5 mm，整个撞击过程的总吸能量为523.7 kJ。

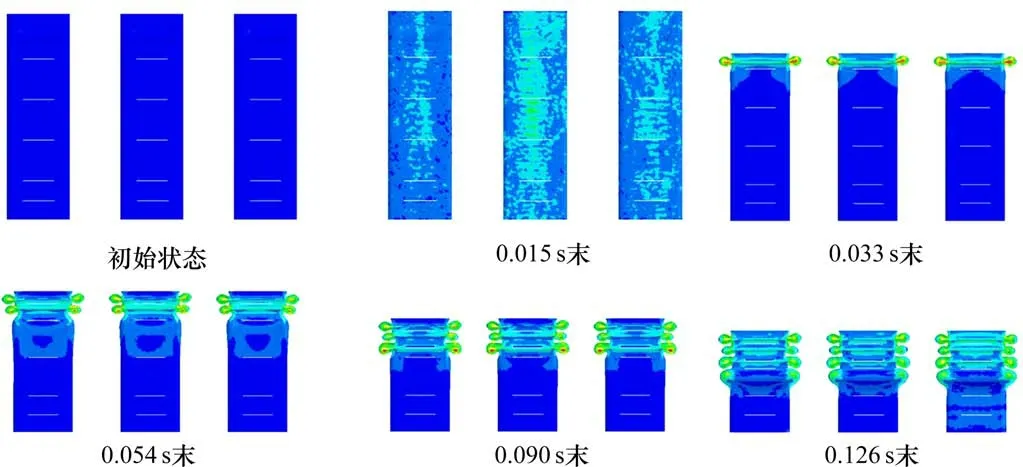
图10 4 mm不锈钢s30408材料薄壁方管仿真结果Fig.10 Simulation results of 4 mm stainless steel s30408 thin-walled square tube

4 有限元仿真和试验对比

从冲击实验和数值仿真得到组件吸能结构撞击力响应的结果可以发现，冲击试验有限元与仿真结果的各项性能指标基本一致。由于加速度传感器触发过程中有一定的滞后性，因此在撞击初期，试验得出的撞击力未出现峰值。实验和仿真得到结构冲击初始峰值力分别为1 973 kN和2 007 kN，相对误差为1.7%。实验和仿真的最终压缩位移分别为404.8 mm和408.5 mm，相对误差为0.9%。实验和仿真平均撞击力值分别为1 450 kN和1 448 kN，相对误差为0.14%。在冲击结束后可知，实验和仿真的最终吸能量值分别为538 kJ和523.7 kJ，相对误差为2.20%。

当结构的冲击动能耗散为0时，台车整体反弹远离刚性墙。图11为实验和仿真得到的吸能结构最终变形模式对比，可以得出，在撞击结束后试验与仿真的变形模式基本一致，整个司机室结构保持完整，没有发生明显的撕裂变形。薄壁方管吸能结构在变形模式、压缩位移、褶皱形状及位置基本一致，均产生对称的屈曲变形。通过对分析比可以得到，冲击试验得到的结构变形非常稳定，3个吸能结构极限变形基本相同，结构冲击试验与有限元仿真结果基本一致，试验和仿真的误差始终在10%范围以内。对于大部件级冲击试验来讲，本文建立的有限元模型具有较高的精度，可以准确模拟实际撞击工况结构的冲击动态响应。因此该有限元模型可用于后续吸能结构耐撞性进一步优化研究，为了节约试验成本，日后可通过仿真手段代替试验研究，进一步探究各个冲击工况下的动态响应。

图11 实验和仿真变形模式对比Fig.11 Comparison of experimental and simulated deformation modes

5 结论

1)司机室在撞击刚性墙瞬间，底架吸能结构诱导槽附近率先发生屈曲变形，结构整体发生有序的屈曲变形，随着撞击的进行，司机室底架边梁发生扭转变形来保障司机室骨架整体后移而不发生失稳。底架整体结构以远离撞击端方向依次发生渐进屈曲，结构在整个过程始终未产生明显撕裂。带隔板薄壁方管吸能结构共产生四级屈曲褶皱，且褶皱产生位置均发生在相邻隔板之间。整个变形模式与预期一致，结构具有符合预期的变形模式及抗失稳能力。

2)通过观察曲线可以发现图中存在4个完整的波峰波谷，分别对应四级屈曲褶皱，试验撞击过程中的平台力为1 448 kN，最大峰值力约为2 007 kN，吸收总能量为550.6 kJ。有限元仿真得到的撞击平台力为1 450 kN，吸收总能量为550.6 kJ。

3)仿真与试验的结果在撞击结束后的变形模式、撞击力、吸能量、变形模式、压缩位移、褶皱形状及位置等方面基本一致，二者各项指标误差始终在10%范围以内，有限验证了本文所设计有限元模型的高精度，为了节约试验成本，日后可通过仿真手段代替试验研究，进一步探究各个冲击工况下的动态响应，为该吸能结构进一步进行优化设计提供理论基础。