多类干扰下的高铁列车运行调整优化模型
2021-10-18徐培娟张大伟彭辉刘丹
徐培娟,张大伟,彭辉,刘丹
(1.长安大学 运输工程学院,陕西 西安710064;2.长安大学 汽车学院,陕西 西安710064;3.重庆市轨道交通集团有限公司,重庆401120;4.长安大学 公路学院,陕西 西安710064)
随着我国高速铁路网络的不断完善,列车运营管理与安全问题一直是研究重点,一些高铁设备故障、恶劣自然环境等事件会影响高速列车的准点运行,轻则造成列车的晚点,重则造成人员伤亡财产损失。因此,在行车干扰事件发生的情况下,如何快速高效的调整出无冲突的列车运行图是提高实际高铁调度生产质量的重要研究内容。近年来,列车运行图实时调整方面的理论与方法的研究是国内外学者研究的热潮,而替代图理论[1]是一种被广泛使用的微观运行图优化方法,多借助启发式算法(如禁忌搜索算法[2]或邻域搜索[3])等方式来缩短计算时间。SAMÀ等[4−5]论证了替代图理论在减少列车晚点时间,避免列车运行冲突方面的实用性,XU等[6]构建了准移动闭塞的行车方式下列车运行调整模型,并实现了列车运行速度的平稳优化[7],但未兼顾列车进路的调整一体化。此外,在解决严重的故障干扰问题时,ZHAN等[8]应用事件−活动网络宏观数学模型求解了高铁区间完全中断情况下的运行调整问题,VEELENTURF等[9]进一步扩展至列车车底运行调整问题。列车运行调整优化是一个超大组合优化问题,曹家明[10]建立单目标线性优化模型,并用对偶算法求解;史峰等[11]松弛列车运行计划,对单线铁路列车运行计划进行调整。孟令云等[12]建立了两阶段带补偿随机期望值模型和不完全连续多阶段决策模型用于列车运行调整。聂磊等[13]指出搜索列车到发顺序的优化组合和列车之间的冲突消解是运行调整的关键环节。庄河等[14]运用马氏决策过程模型和策略优化方法从宏观角度建立高速铁路列车运行调整模型。本文结合中国高速铁路列车的需求,进一步创新扩展替代图理论,完善其在准移动闭塞控制下的运行图优化调整理论,实现列车车站进路的同步调整,实现最短的时间内提供出无冲突的较优的运行图优化调整方案,为行车调度指挥工作提供策略或指导意见。
1 问题描述
在高速列车运营过程中,线路自身状况、沿线自然环境或设备的状态会直接影响列车的运行,即行车干扰事件,此处研究的干扰类型包括初始晚点、闭塞区间限速及车站到发线不可用(中断)。3种干扰情形具体如下:
1)列车初始晚点情形:列车进入指定的线路范围前,受随机干扰的影响在运行中产生了初始晚点,假设列车初始晚点符合三参数韦布尔分布:
2)限速类干扰情形:受恶劣天气(雨、风等)、线路故障或维修活动影响,列车在通过指定线路区段时应降速运行。限速的起始时间、影响范围、限度等级均是可变的。
3)到发线不可用:当车站到发线受一些设备故障或维修活动的影响,不能接发列车。
2 基于替代图理论的列车运行与到发线调整优化模型
铁路列车在线路上运行,列车对每一闭塞区间的占用类似与于工作车间中零件加工对机器设备的占用问题(称为工作车间调度问题),MASCIS等[15]将列车运行调整视为工作车间调度问题,D'ARIANO等[1]并将替代图理论用于求解铁路类的工作车间调度问题。具体表现为:将铁路区间视为“工作车间的机器”,将列车视为“代加工零件”,同一时刻机器只能加工一个零件。利用替代图表现为,区间视为“节点”,列车由一个区间运行至另一个区间的过程视为“有向弧”,因此,列车在线路上运行的活动转化为一张有向图,利用图理论,最终为所有列车找到由起始“节点”到“终点”的唯一路径,使得图中最长的路径的长度最短(即“耗时最短”)。基于上述理论,建立研究模型。模型建立前的假设:
1)3类干扰事件不会导致列车取消事件;
2)高铁列车的速度划分为5级,列车速度等级的变化符合列车牵引曲线要求;
3)干扰事件发生时,闭塞区间限速的相关参数及车站到发线不可用的相关参数已知;
4)通过列车在车站不可变更到发线,只有在站有停车作业的列车可变更到发线。
2.1 基本参数及变量
根据铁路线路闭塞区间、列车运行的基本要素,令T表示列车集合;S表示线路闭塞区间集合;ϑη表示第η个区段内的闭塞区间集合;fη,lη分别表示该区段第一个或最后一个闭塞区间;sw表示有道岔的闭塞区间集合;ST表示所有车站内到发线的集合(属于列车在车站可选择的区间),Sγ⊂ST,γ表示车站标号,车站γ内到发线和正线区间的集合。优化模型中设以下决策变量:
ωt,s为列车t开始占用闭塞区间s的时刻;zt,s为0,1变量,列车t是否占用选择区段s,若选择为1,不选择为0;λi,j,p,q为无速度要求的可选择弧变量,确定列车i,j占用闭塞区间p,q的顺序;μi,j,η为有速度选择的可选择弧变量,确定列车i,j占用区段η的先后顺序;βξ,t,s为速度等级变量,列车t在闭塞区间s的是否采用速度等级ξ;xt,s,y为限速影响判定,列车对应时间ωt,s是否在第y个限速发生开始时间点W1,y之前;xˉt,s,y为限速影响判定,列车对应时间ωt,s是否在第y个限速发生结束时间点W2,y之后;devt,s为0,1变量,判断列车是否在车站变更到发线,=1,表示列车变更到发线,否则=0;其中(t,s)∈Rt,station;det为列车t运行全程变更到发线的次数。
2.2 目标函数和约束条件
模型目标函数的建立从满足旅客和行车调度员的双重角度出发,即为尽可能降低列车的二次晚点时间,并尽量减少列车在车站频繁变更到发线的次数,保证车站正常的生产活动次序。因此,目标函数如式(1)所示。

式中:ωt,end表示列车t占用最后一个闭塞区间的时刻;et,s表示列车t进入线网第一个闭塞区间s时的开始时间;ct表示列车t的计划旅行时间;dtt表示列车初始晚点时间;α1和α2分别表示列车晚点和变更到发线次数的权重。
2.3 约束条件
2.3.1 列车区间最小运行时间约束
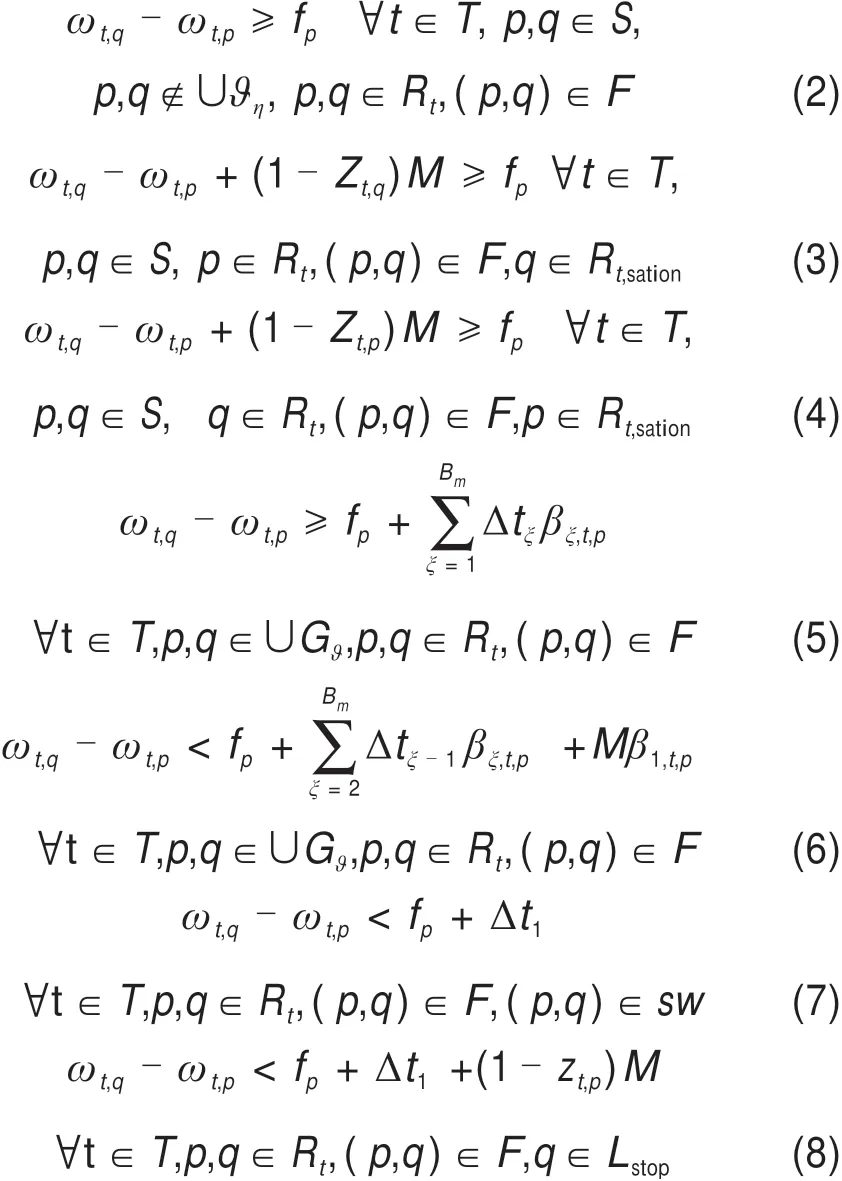
式(2)~(8)对列车在每一闭塞区间的运行时间约束,其中fp表示全速运行时列车在闭塞区间p的最短的运行时间;Rt表示列车t在固定路径中途经的闭塞区间集合,Rt⊂S;F表示线路构成的固定弧集合,F={(p,q)|p,q∈S},p,q代表铁路线路中连续2个闭塞区间;M表示极大正数;Rt,station表示列车t在所有车站内可选择的路径集合;Δtξ表示相比于全速运行,列车在速度等级ξ下产生的附加运行时间;Gϑ表示非车站区域的闭塞区间的集合;B表示连续2列车之间需要保持的空闲闭塞区间数集合,B={ξ|ξ=1,2,3,4,5},也表示列车的速度等级,其中Bm表示全速运行时所需的空闲闭塞区间数,也表示全速等级;Lstop表示车站到发线的集合。结合各符号含义,式(2),(5)和(6)计算列车在某一速度等级要求下通过该区间的最小运行时间,其中式(5)和式(6)对某一速度等级下的运行时间的阈值进行了界定;式(3)和式(4)定义了若是列车进入或驶出可选择的闭塞区间时所对应的运行时间约束,只有闭塞区间p被选择后,即zt,p=1,这2个公式才能起到约束作用;式(7)和式(8)对应了道岔闭塞区间、车站正线闭塞区间列车不可停车的约束条件。
2.3.2 列车车站到发时间约束

式中:ET表示每列车进入路网时对应的第一个闭塞区间的集合,ET={t∈T,s∈Rt,s是Rt中的第一个区间};Dt表示列车t停车对应的到发线的闭塞区间集合,Dt⊂S;dt,s代表列车t在各个到发线的最小停站时间,s∈Dt;pt,s+1表示列车t在车站γ的计划发车时间s∈Dt;虚拟的起点时间t0=0。约束条件(9)对列车进入待研究线网的驶入时间和初始晚点干扰的共同约束,公式(10)对列车在停靠站的出发时间进行约束,而约束(11)表示了列车在可能进行上下客作业的到发线上应满足最小时间停站时间的约束,以保证旅客的上下车服务。
2.3.3 列车区间运行速度约束
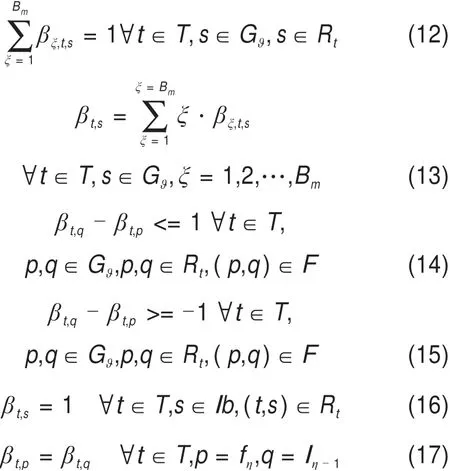
约束条件(12)~(17)描述了列车在闭塞区间运行时的列车速度等级的约束,(12)表示了在每一个闭塞区间每列车只对应一个速度等级,约束条件(13)根据βξ,t,s的0,1取值计算出列车的实际速度等级,式(14)和式(15)表示列车在连续的2个闭塞区间运行时,列车的速度等级差最多为1个等级。式(16)表示列车在进入有停站计划的车站前后,列车在站前进站或站后出站,列车的速度等级最低,lb表示停站计划列车的速度最低的对应闭塞区间集合;式(17)则要求所有列车在上一个区段的最后一个闭塞区间(lη-1)和下一个区段的第一个闭塞区间(fη)的速度等级一致。
2.3.4 列车运行间隔和路径选择约束

式中:δp,q表示可选择弧(p,q)对应的列车i,j之间的最小追踪间隔时间,即使用一对可选择弧的最短的间隔时间;A表示可选择弧集合,A={p,q|p,q∈S&(p,q)∈F},确定列车顺序,消解冲突。约束条件(18)~(19)描述了列车在车站选择道岔、到发线时,不同列车对同一个可能占用闭塞区间的约束,约束条件(20)和(21)表示列车之间对可能占用到发线或站内正线闭塞区间到第一出站进路区域的占用顺序,式(22)和式(23)表示列车对出站进路的占用顺序。


式(24)将列车在这些实际未被列车占用的到发线或进路的开始时间设置为0;约束(25)要求在车站直接通过的列车不允许变更到发线,列车直接利用车站正线区域通过,st_valuet,p表示原计划运行图中列车是否在车站有停站计划,若直接通过其值为1,否则为0。式(26)规定每列车在每一个车站只能占用一条到发线或正线。式(27)和式(28)用于计算相比于原计划到发线使用计划的变更情况,若为1则表示变更。式(29)计算每列车变更到发线的次数。
2.3.5 准移动闭塞区间列车追踪运行约束

式(30)和式(31)表示在准移动闭塞控制下,列车在两车站之间的闭塞区间运行时,以不同速度等级追踪运行,列车速度等级与之相匹配的列车间隔空间距离约束。列车在正线区段不能越行,因此对这些闭塞区间先后占用顺序不变,变量μi,j,ϑ表示列车在整个区段的运行顺序[6]。
2.3.6 限速故障干扰约束

式中:T1y,T2y分别表示第y个限速事件的开始时间和结束时间;表示第y个限速干扰的最高限速等级,表示第y个限速事件影响的闭塞区间集合,式(32)和式(33)表示多个限速事件干扰下,对列车受限速影响的空间和时间范围的精确判断;在此基础上,利用式(34)实现对受影响列车运行速度的限制。
3 模型求解与算法设计
优化模型为混合整数线性优化模型,是一个复杂的组合优化问题,属于NP-hard问题。模型中列车运行时间点、速度、列车顺序等变量随着线路闭塞区间数和列车数急剧增加,尤其是列车运行速度和列车的车站进路的选择,对列车运行动态调整问题提出了很大的挑战。因此,为实现模型的高效求解,设计两阶段求解方法,通过商业软件Cplex辅助求解,通过缩短初始解的求解时间,提高初始可行解的质量,来加速此复杂模型的求解。模型求解流程图,如图1所示,具体求解思路如下。
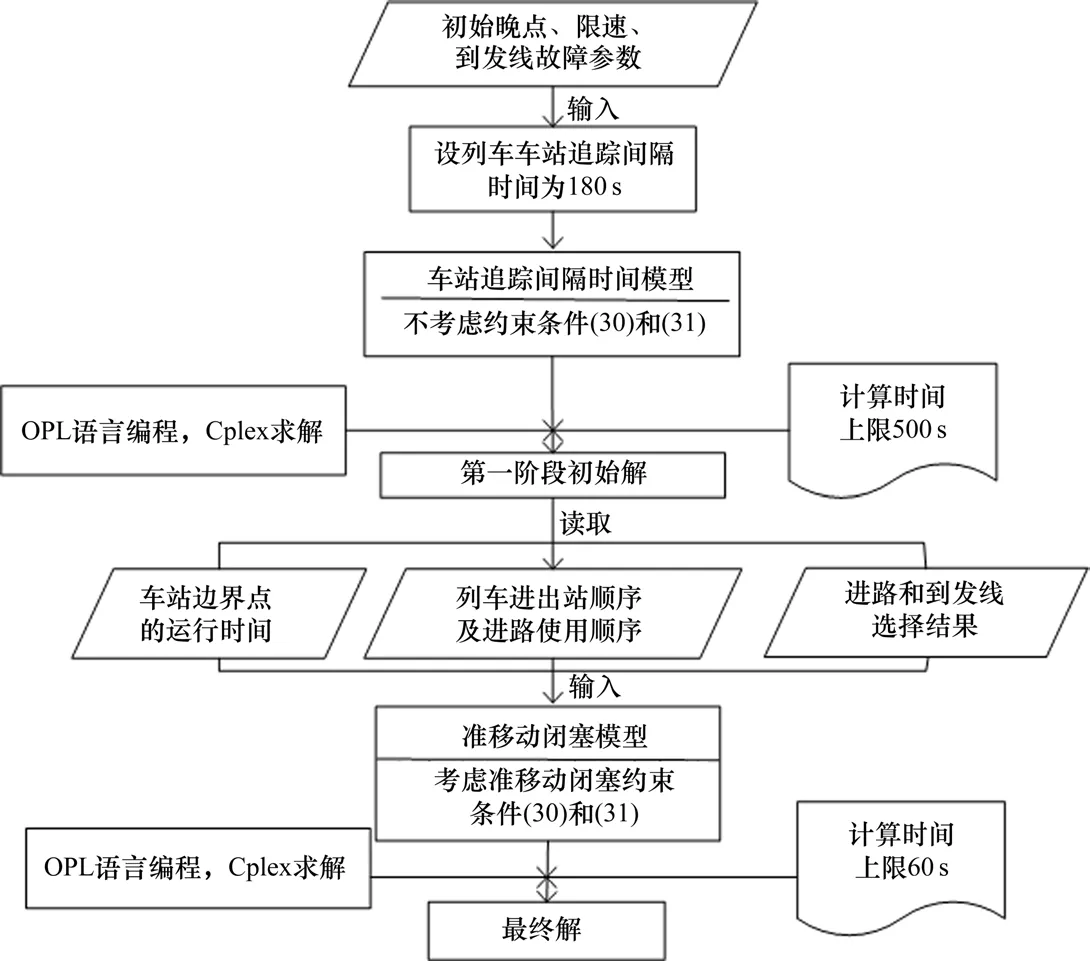
图1 两阶段近似算法流程图Fig.1 Two-stage approximate algorithm
第1阶段:针对3种干扰参数,固定部分最不可能受限速干扰的列车运行速度,使列车的区间运行速度尽可能的最大;利用时间间隔法完成车站区域列车进路的排列或冲突的疏解,将列车之间在车站的到发间隔控制在120 s以上;忽略闭塞区间列车准移动闭塞追踪间隔约束(式(30)和式(31))。利用Cplex系统默认算法,计算出调整后数学模型的最优解;
第2阶段:从第1阶段的解集中提取出列车进入车站区域各闭塞区间的时间,在车站到发线的调整顺序,进路占用顺序,进出站顺序的相关解值,输入本论文建立的准移动闭塞优化模型中。利用Cplex对列车闭塞区间准移动闭塞的间隔法进一步的调整优化,得满足整条线路上的列车追踪运行的条件。
经多次算例实验得出第1步计算时间是全过程中求解时间的关键,在后续案例计算过程中,设第1步的计算时间上限为500 s,第2步的计算时间为60 s。
4 算例分析
4.1 基础数据
以我国某高速铁路中的一个调度区段内的线路和列车为对象,包含6个车站,6个线路区段,线路长度为500 km,划分为374个闭塞区间。线路区间布置与干扰事件信息详见图2。研究运行图时间段为1.5 h,期间有20列高速列车运行,列车最高运营时速均为300 km/h。采用列车运行图是基于实际高铁线路情况,生成相较于实际生产发车更为密集繁忙的样本运行图。列车在每个闭塞区间的运行时间及各速度等级对应的附加运行时间如表1所示。此外,列车二次晚点时间和变更到发线次数在目标函数中的权重设为α1=1,α2=1。

表1 速度等级和对应的附件运行时分Table 1 Train speed levels and their additional running times

图2 车站线路布置及故障干扰信息Fig.2 Parameters of railway infrastructure and disturbances
4.2 结果数据分析
4.2.1 计算时间对比分析
在考虑4.1节介绍的限速和到发线不可用的干扰情况下,分析求解调整后的列车运行图的质量。将上述算例参数输入所设计的算法程序,分析解的求解时间,与此同时,对比分析了另一种算法思路(先固定列车运行速度计算初始解,然后将初始解带入速度可调控的原设计模型,求解最优解[6])的求解效果,记为参考算法。以所有列车准点运行情况下的运行图调整效果为例,如图3所示,实线曲线代表设计算法的解值随着计算时间的变化趋势,当计算时间为第500 s时,模型求解出调整后的列车运行图中列车2次晚点和列车变更到发线顺序的总和为到8 500;图中虚线表示采用参考算法模型解值随计算时间收敛的趋势,在第1 700 s时,该算法所能提供的解值为115 000左右,远远大于设计算法求解值8 500,解的质量远低于设计算法的求解值。
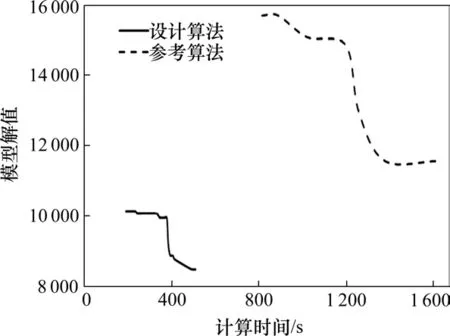
图3 2种算法计算时间对比Fig.3 Comparison of efficiency between two algorithms
4.2.2 调整后运行图结构分析
在3种故障干扰影响下,通过模型计算绘制出调整后的列车运行图。如图4和图5所示,分别表示利用算法第1阶段求解的初始解的运行图和第2阶段调整后的最终运行图。如图4可知,虽然算法消除了列车在车站区域到发线的冲突,保证列车以最小的追踪间隔时间在车站到发,但是忽略了闭塞区间列车追踪运行的最小空间间隔,导致前后两列车的运行线出现交叉或重叠,如图4中虚线圈所示。相比图4而言,模型进一步将闭塞区间列车的冲突疏解开,进一步提高了调整后的运行方案的质量(如图5)。此外,从调整优化后的运行图可知,优化模型能够实现:1)在限速区段能够将列车的运行速度控制在最大允许速度之内;2)优化控制列车运行速度,满足了列车加减速的车体性能需求;3)模型实现了多个限速干扰事件的同步求解;4)调整后的运行图结构合理,紧凑,无冲突,满足实际生产需求。

图4 车站间隔时间法调整后运行图(第1阶段)Fig.4 Timetable rescheduled after the first stage computation

图5 准移动闭塞法调整后运行图(第2阶段)Fig.5 Final timetable rescheduled after second stage of computation
4.2.3干扰事件影响分析
为分析列车在准点或初始晚点情况下受不同等级限速干扰的影响,进一步计算分析结果如表2所示。其中限速等级k表示所研究的高速铁路线路中2处限速干扰事件发生时允许列车通过该区段的最高速度等级,其值越低表示限速值越低;晚点时间表示研究区域内交通晚点的总时间(单位:s);速度等级差表示调整后运行图中列车在每一区间运行时的速度等级(1,2,3,4,5)与未受干扰情况下列车在每一区间运行时的速度等级之间偏差的绝对值;到发线变更次数指的所有列车对车站到发线的使用情况与没有干扰事件发生时到发线使用情况的变更次数。由图5数据可知,严重的限速等级干扰或者有初始晚点的干扰情况下,引起的列车晚点时间更长;而且严重的限速干扰使得列车的运行速度等级与既定的速度等级的偏差增大。对于目标函数的参数取α1=1,α2=1时,限速等级未能影响到列车变更到发线的次数,均为14次。然而,在更复杂的或更繁忙的运行图中,列车变更到发线的次数需要进一步的研究。
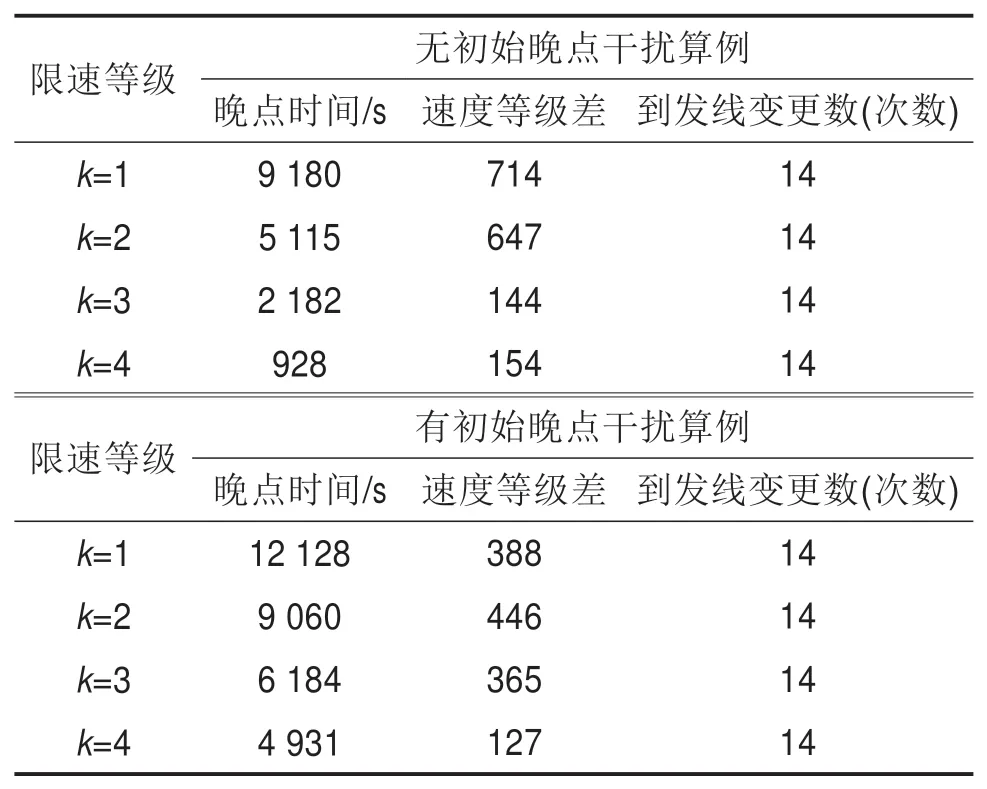
表2 故障影响数据Table 2 Data related the influence caused by different disturbances
5 结论
1)针对多类干扰列车运行干扰事件建立混合整数线性优化模型,模型同步实现了列车运行调整和列车运行径路调整,并设计了两阶段算法,实现复杂数学问题的快速求解。
2)相比时间间隔法,模型中采用的距离—速度间隔法的设计进一步提高了列车在区间追踪运行的可靠性,模型对列车在到发线使用的调整进一步提高了。
3)对于模型中目标函数的权重系数的设定以及算法的求解效率未来需要进一步的研究优化。
