椭圆函数在滤波器上的应用

卓群忠

(福建广播电视大学莆田分校，福建 莆田351100)

上世纪初，研究人员在双模准椭圆函数方面的研究上取得了一定的成果，同时将这一理论应用在了滤波器的谐振单元中，形成了L型结构耦合单元。新世纪初，Lung-Hwa Hsieh和Kai Chang等人的研究促进了椭圆函数滤波器的发展，他们通过将圆环谐振器和间隙耦合发明了紧凑型的椭圆函数滤波器。没过多久，Lung-Hwa Hsieh和Kai Chang等人又通过耦合臂和方形环搭配谐振电路设计出了L型支节耦合的双模准椭圆函数滤波器。之后，吴胜阳概括总结了椭圆函数低通滤波器的工作原理和设计方法，通过对MATLAB的仿真，结合椭圆函数的设计步骤，给出了一个能够在微带线上的椭圆函数低通滤波器设计方案。综上，对于椭圆函数滤波器的研究并不少见。文章就椭圆函数的定义和推导出发，介绍椭圆函数在滤波器中的应用，以及椭圆函数的响应特性，综合阐述椭圆函数在滤波器方面的应用及发展。

1 椭圆函数基本概念

1.1 椭圆函数

雅可比椭圆函数是椭圆滤波器的数学基础，通过积分的思想方法，借助勒让德第一类椭圆积分导出其具体性质：

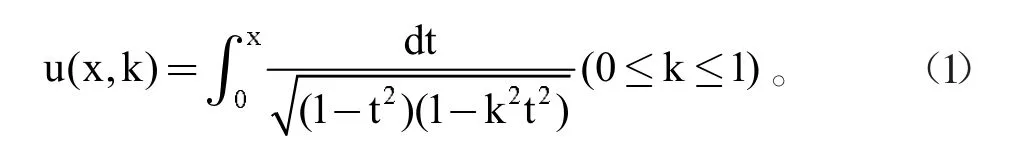
在我们研究的范围内，参数k是小于1的实数，称为模数，把t做如下代换：

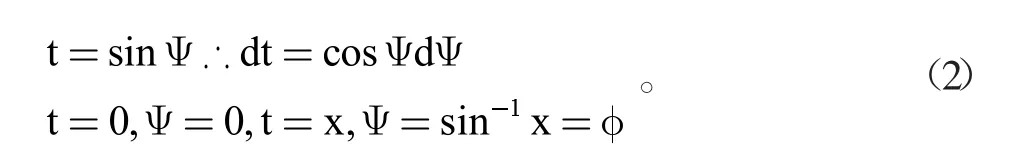
第一类椭圆积分可以推导出以下函数：

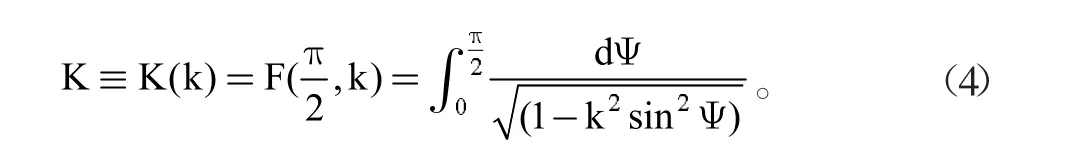
椭圆积分顾名思义，与椭圆的性质有很大关系，具有对称性，同时也具有周期性，因此任意实数k的函数值都能够在0≤Ψ≤π/2周期内的计分表中获得。

要是把公式(2)的积分上限φ当作是u和k的函数，那么可以引入符号：φ=am(u，k)，其中φ称为以k为模的u的幅度函数，通过变换可以获得x=sinφ=sin am(u，k)，这就是以k为模的雅可比椭圆正弦函数。

1.2 椭圆函数的性质

函数：

这个函数的极点是当sn(u，k)的函数值为零的地方，此时u=0，因为sn(u，k)=0，并且是关于4K和j2K'双周期函数，因此函数sn(u，k)的极点为2mK+j(2n+1)K'，这里的n，m是一个整数。因为n阶椭圆函数具有低通的性质：

这个函数当中，如果n是一个奇数，那么这个函数的特征函数是：

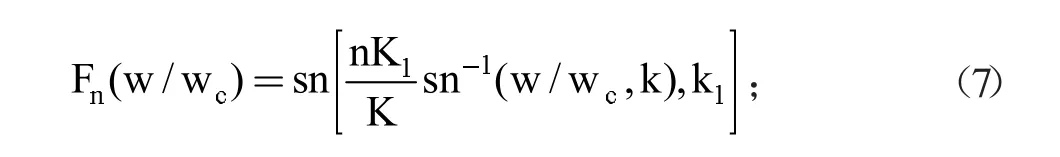
如果n是一个偶数，那么这个函数的特征函数是：

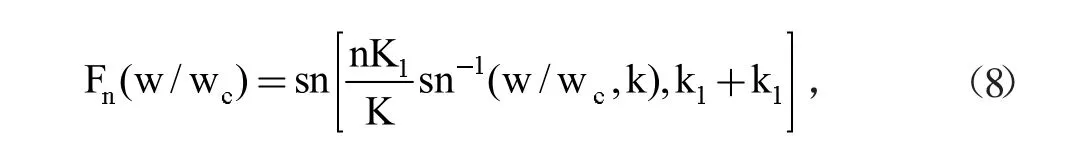
函数中K1=K(k1)；K=K(k)被定义为全椭圆积分，这两个函数的模为k1和k。Fn(w)是一个特征函数，这里可以得到有理函数(这个有理函数是两个含w的多项式比值)，有理函数定义域范围内包含的零点完全落在阻带范围内，并且定义域内的所有极点也全部在阻带范围内。例如：令n=3，k=1/1.4=0.71429，可以获得Fn(w)，通过积分表可以获得K=K(k)=K(0.71429)=1.86282，式中θ=sin-lk=45°35'，则可得出：

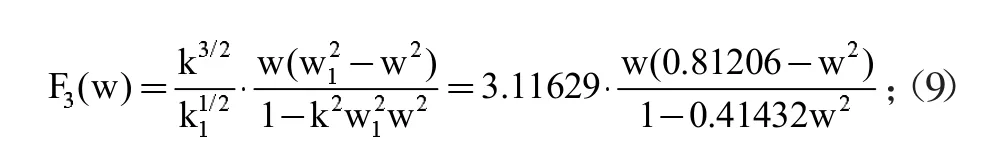
当n=4(偶数)，k=1/1.4=0.71429

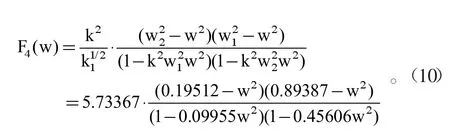
1.3 滤波器中椭圆函数的数学模型

椭圆函数的性质应用于滤波器，需要对其的数学模型进行确定包括椭圆函数特征函数的相关参数，物理上表现在滤波器上的性能为衰减特性、工作传输函数，通过数学模型能够把滤波器的电路图和相关的电器元件参数进行设计。

衰减特性为：

式中y0=ω/ω0。

这个衰减特性函数的特征函数为：

式中v=1，…，n；k=1，…，(n-1)/2，s作为复归一频率，有函数s=jy，s(v)为传输函数的自然模式，即传输函数的零点；pk是衰减函数的衰减极点，存在于阻带的范围内；c(v)是衰减函数的衰减零点，存在于通带的范围内；n是电路阶次。切比雪夫近似在数学上表现为过渡带趋于∞时，椭圆函数能够获得的数值，可以通过一系列的递推公式获得奇阶椭圆函数近似。通常来说，能够获得两个递推公式，依照正向的递推公式，能够获取切比雪夫近似的一般通式，同时在这基础上能够利用反向递推的方法，获得椭圆函数的相关模型，进而可以获得椭圆函数滤波器的电路形式和电路元件的相关数据。

公式(6)的变化中，能够获得特征函数为零的频率点，这些点对应着传输函数的最大值：

这个函数当中，如果n是一个奇数，那么可以获得：

如果n是一个偶数，那么可以获得：

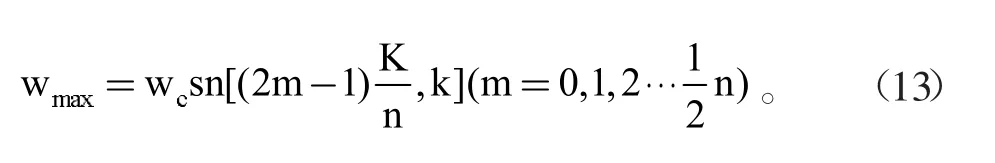
理论上能够获得的最小通带增益为：

这个值对应于Fn(w)=±1。

这个函数当中，如果n是一个奇数，那么可以获得：

如果n是一个偶数，那么可以获得：

所以理论上可以获得的直流增益是：

函数值的曲线上有一个极点(最低点)，此时通带上有w=wc，可以获得对应于n的最小增益都有：

H是一个固定值的情况下，ε(波纹因子)主要是通带中峰表现。其中波纹和通带的数学关系为：

阻带能够得到的最低点是零，为特征函数的极点，因此：

所以理论上可以获得的阻带增益是：

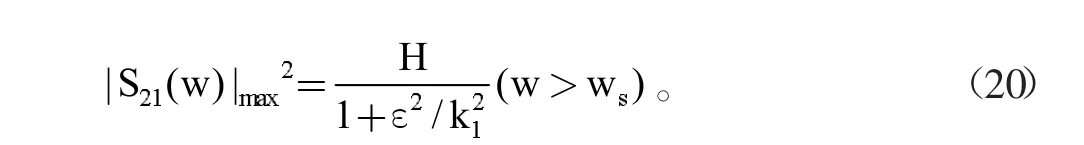
这时的频率为：

阻带衰减量与k1，ε的函数值之间有如下关系：

增益特性从通带到阻带单调地减小，一般会把阻带边缘对应的增益下降到最大处频率称为ws。这就有如下关系式：

能够获得F为：

K为选择因子，其倒数为陡度，表征过渡带增益特性。

1.4 椭圆函数滤波器

椭圆函数为基础的这一类滤波器具有有限传输点，具有等波纹的特点，定义传输函数为：

这个函数中，Ω为角频率，通过第一类雅克比椭圆函数积分获得，函数Fn(Ω)是关于Ω的函数。通过函数信号图像的绘制，可以获得椭圆函数滤波器的频响曲线，见图1。

图1 椭圆函数滤波器频率响应衰减特性

2 椭圆函数滤波器的应用

通常微波滤波器有多种形式，滤波器的频率响应主要有巴特沃兹型、切比雪夫型和椭圆函数型。巴特沃兹型滤波器要需要更多的阶数，这就使得这种滤波器的设计更为复杂，而椭圆函数滤波器能够使滤波器获得更好的选择性，相较于另一种切比雪夫型滤波器，设计结构上更加简单易行。椭圆函数滤波器在设计中，通常使得其组成中相关的谐振电容电感器件成对排布，因而相比较与另外两种滤波器，椭圆函数滤波器的性能更加优越。同时在设计过程中，能够利用椭圆函数的元件选择，对椭圆函数滤波器的性能进行调节，从而使得椭圆函数滤波器在寄生效应方面具有更大优势，能够让系统S参数曲线更加符合预期。

吴胜阳概括总结了椭圆函数低通滤波器的工作原理和设计方法，通过MATLAB的仿真，结合椭圆函数的设计步骤，给出了一个能够在微带线上的椭圆函数低通滤波器设计方案。贾晓斌等采用了一种新的归一方法，该方法基于DDS，能够利用EDA软件对Muhisim2001进行仿真，通过对椭圆函数滤波器的结构，物理参数，电阶数等方面进行设计，他的设计让他获得了具有一定的较快衰减特性，并且幅频性能也具有一定的优势的160MHz的7阶椭圆函数滤波器。他的设计方案能够应用于不同频段、阶数、类型的滤波器设计。李婵娟等以椭圆函数低通滤波器为基础，设计了一款能够克服以往滤波器结构过大，渡带衰减慢等问题的高低阻抗线微带低通滤波器，主要是利用了椭圆函数，设计给出了这种滤波器相关参数的理论计算方法，利用ADS和HFSS对滤波器的设计进行了模拟优化，并最终做出了实物，展开测试验证，获得了较好的实验结果，证明了他的设计方案是有效的。董利芳基于传统的高低阻抗线结构滤波器，利用椭圆函数设计了低通滤波器，能够应用于微波平面电路，通过HFSS仿真模拟可以获得，该滤波器的过渡带较传统滤波器更陡峭，同时也具有更加宽泛的频域，并且在物理结构上能够减小使用材料，减小体积和结构复杂性。

3 结论

椭圆函数滤波器具有更高的选择性和更好的性能优势，在设计中，通常其组成中相关的谐振电容电感器件成对排布，椭圆函数滤波器的性能更加优越。同时在设计过程中，能够利用椭圆函数的元件选择，对椭圆函数滤波器的性能进行调节，从而使得椭圆函数滤波器在寄生效应方面具有更大优势，让系统S参数曲线更加符合预期，并且以椭圆函数为基础的这一类滤波器具有有限传输点，等波纹特点，因而能够应用于高性能滤波器。