灰狼算法优化分数阶模糊控制器参数

范 鲁 娜(河南艺术职业学院文化传播技术学院 河南 郑州 450002)

0 引 言

分数微积分已经被研究了将近3个世纪，并且已经被科学家广泛应用到科学与控制工程领域中[1]。分数阶PID控制系统是由斯洛伐克学者Podlubny[2]于1994年提出，并应用于分数阶模糊系统中。在此项工作之后，其他的工程师应用不同的设计与调整方法设计出分数阶PID控制器。分数阶微积分为复杂成比例的系统过程和事件提供完善的数学模型，应用于物理、生物与控制理论方面[3-5]。

分数模糊控制器(FFCs)是传统模糊控制器与分数阶算子结合，在多种动力系统中表现出比传统的模糊控制器更好的性能。分数阶模糊控制器中的参数估计问题一般用进化算法去优化求解，提高控制器的精度与稳定性能。例如：用遗传算法模糊分数阶控制器模型问题[6]；用混沌粒子群算法对可再生发电混合动力系统进行分数阶模糊控制器[7]；使用微分和声搜索算法设计分数阶[8]；采用改进的重力搜索算法对抽水蓄能水电机组进行快速模糊分数阶PID控制[9]；分数阶模糊PID控制器在机械手臂中的应用性能分析[10]；社会蜘蛛群算法对分数模糊控制器参数标定[11]。虽然这些算法都获得比较理想的结果，但是仍然具有一个很重要的局限性，由于其搜索策略中的勘探与开采之间的平衡关系，容易陷入局部最优的解，这种行为会导致整个种群快速集中在最优粒子周围，容易形成早熟收敛，不利于搜索空间的探索[12-13]。

灰狼优化算法是由Mirjalili等[14]于2014年提出的新型群智能优化算法。灰狼优化算法(GWO)是模拟灰狼的狩猎机制，包括搜索猎物、追踪猎物、包围猎物与捕杀猎物等步骤，与其他的元启发式优化算法不同，该算法考虑领导阶层。由于该算法具有较好的平衡勘探与开采能力，所以该算法越来越受到相关领域的人们重视，并成功地应用于一些实际工程问题中。如Gupta等[15]利用GWO对电力系统比例积分控制器的参数进行评估，Chaman-Motlagh[16]利用GWO设计一种具有三到五根椭圆棒的超陷光子晶体滤波器,Sulaiman等[17]利用GWO解决了电力系统中无功优化调度问题。本文用灰狼优化算法优化分数模糊控制器参数，主要是因为灰狼优化算法原理简单，需要调节的参数少，而且在寻找全局最优解时具有较好的求解效率与较高的求解精度。

1 分数阶模糊控制系统数学模型

分数阶控制系统的特征是微分方程，在动力系统或控制算法中，分数阶通常用微分或积分模型表示[18-19]。

1.1 分数阶微积分

(1)

式中：a和t表示操作算子的上下限；α表示分数阶阶次且α∈R；τ表示切向单位向量。最常用的分数阶微积分定义是Riemann-Liouvile(RL)和Grunwald-Letnikou(GL)。分数阶微分阶α被定义如下：

(2)

在分数阶导数的数值计算中，α阶导数在kh(k=1,2,…)点，具体表示如下[11]：

(3)

(4)

然后，分数阶差分方程的一般数值解被定义如下：

(5)

1.2 分数阶近似值算子

(6)

式中：hα(k)是脉冲序列；Tc表示采样频率。在文献[23]中已经证明了有理式模型比多项式模型具有更快的收敛速度。因此采用Pade近似的方法，利用文中给出的定义，从脉冲响应中得到分数阶模型，具体模型表示为：

(7)

式中：m、n与参数ai、bi是通过调节hα(k)的系数m+n+1得到。

2 模糊控制器

模糊控制器是模拟专家的经验，并用语言形成严格的控制规则，然后通过控制规则控制其计算，实现目标任务。模糊控制器的一个重要的特性是将控制方案划分为多个区域[24]。在每个区域，控制策略都可以通过使用一个规则来简单地建模，该规则将特定的操作按照所形成的区域关联起来。在所列出的文献中，尽管提出了几种模糊控制器模型配置，但是本文选取模糊分数阶PDα+I模型结构，因为此结构具有较好的稳定性与鲁棒性[6]。

控制器配置如图1所示。其中：E、DE和IE分别代表误差、偏导误差和积分误差；e表示偏差值；v表示模糊输出量；Kp、Kd、Ki、Ku为增益值，前三项表示输入项，后一项为输出项。控制函数u是E、DE和IE的非线性映射函数，表示如下：

u(k)=(f(E,CE)+IE)Kuu(k)=[(f(Kpe,KdDαe)+KiIe)]·Ku

(8)

图1 模糊PDα+I控制器

3 GWO

灰狼优化算法是新型的群智能优化算法[14]，该算法的灵感来源于灰狼群落的领导、指挥与狩猎行为。在该算法中，灰狼群被划分为四组，分别为α、β、δ、ω，前三种类型是作为领导阶层，ω是最底层灰狼种群，追随前3种种群。α、β、δ灰狼种群的更新公式如下：

D=|C·Xp(t)-X(t)|

(9)

X(t+1)=Xp(t)-A·D

(10)

A=2a·r1-a

(11)

C=2·r2

(12)

式中：D表示灰狼与猎物之间的位置距离向量；t表示当前的迭代时间；A、C是向量系数；Xp是猎物的位置向量；X是灰狼的位置向量；a是步长因子，随着迭代次数的增加由2降到0；r1、r2取[0,1]间的均匀随机值。

在GWO中，认定α、β、δ为捕食猎物的最好的值，在优化的过程中，α、β、δ被认为是最好的解，其他灰狼为ω，不断更新位置朝向α、β、δ种群。根据以下数学模型，调整ω狼群的位置：

Dα=|C1·Xα-X|

(13)

Dβ=|C2·Xβ-X|

(14)

Dδ=|C3·Xδ-X|

(15)

式中：Xα表示α灰狼的位置;Xβ表示β的位置;Xδ表示δ灰狼的位置;C1、C2、C3是随机值；X表示当前解决方案位置。用式(13)、式(14)和式(15)分别计算当前解位置与α、β、δ灰狼位置之间的距离。定义距离之后，当前解的最终位置计算如下：

X1=Xα-A1·(Dα)

(16)

X2=Xβ-A2·(Dβ)

(17)

X3=Xδ-A3·(Dδ)

(18)

(19)

式(13)-式(15)定义了ω灰狼步长分别朝向α、β、δ灰狼位置。式(16)-式(19)定义了ω灰狼最终的位置。A、C这两个向量是随机值，能够有效平衡GWO勘探与开采能力。

Mirjalili 等[14]提出的GWO相比于其他著名的元启发式算法具有很高的性能。该算法具有很强的探测能力，而且能够避免局部最优。此外，较强的平衡勘探与开采能力能够有效解决一些复杂的工程问题。因此应用GWO优化模糊控制器参数问题。

4 用GWO对分数阶模糊控制器参数优化

在分数阶模糊控制系统的设计阶段，将参数计算过程转化为一个多维优化问题，将分数阶模糊控制器参数作为决策变量。在这种方法中，优化问题的复杂性往往产生多模态误差曲面，其代价函数往往难以最小化。提出一种分数阶模糊控制系统参数优化标定算法，采用GWO确定最优的参数值，如图2所示。

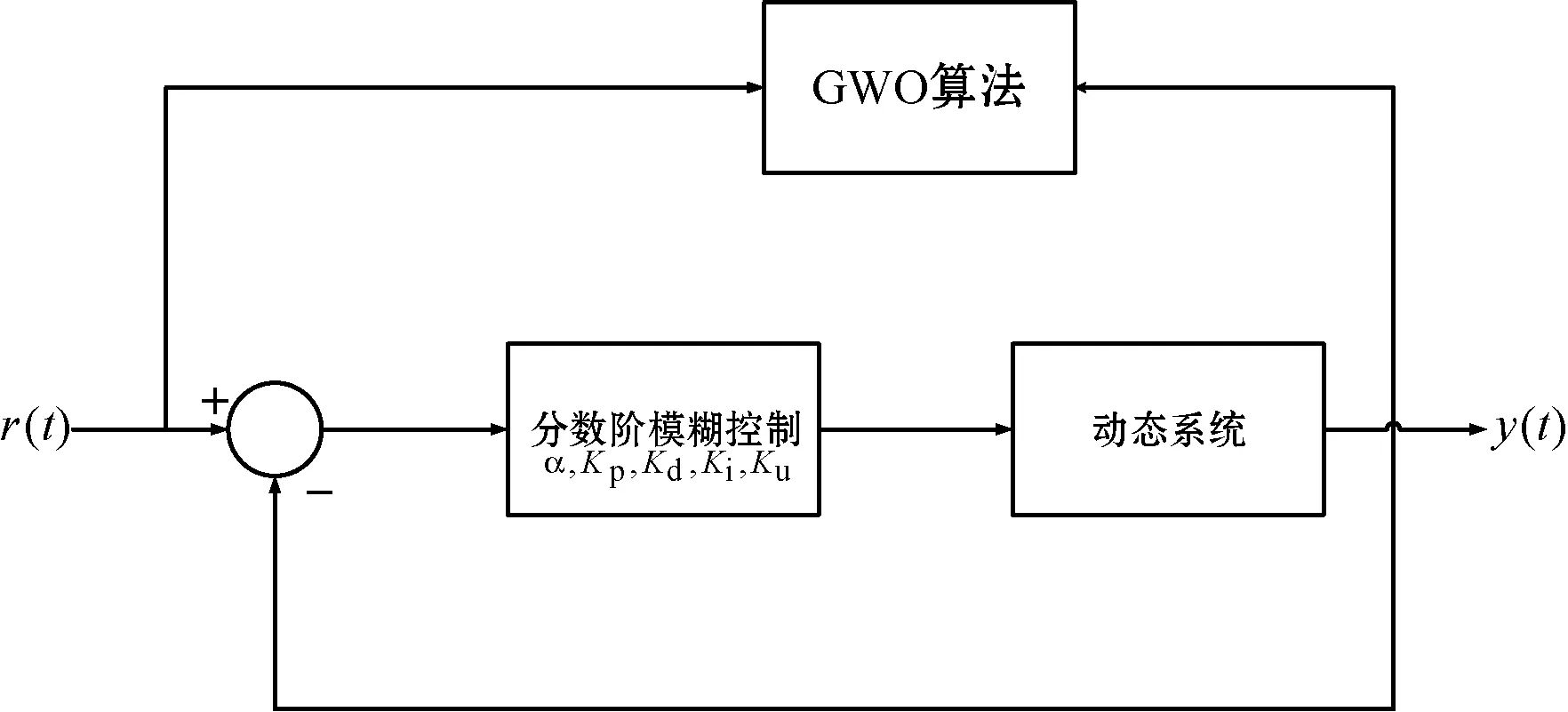
图2 基于GWO优化模糊控制器的参数问题

在GWO求解模糊控制器参数问题中，GWO中的最优解表示分数阶模糊控制器的一组最优的参数。分数模糊控制器参数(α，Kp,Kd,Ki,Ku)确定GWO候选解的维度。GWO的生物空间对应分数模糊控制器参数整定的解空间。另外，GWO的评价函数是分数模糊控制器的积分时间绝对误差(ITAE)[25]。ITAE指标J由以下模型定义：

(20)

式中：y(t)表示闭环阶跃响应函数;r(t)表示阶跃函数。

最小化目标函数为：

J(X)X=(α,Kp,Kd,Ki,Ku)∈R5

(21)

约束函数为:

0≤α≤3

0≤Kp≤5

0≤Kd≤5

0≤Ku≤5

控制器的参数值对控制器的性能具有较高的影响。例如，比例系数Kp值增加时，系统会变得敏感，响应速度更快，系统的稳态误差得以减小，从而使控制的精度提高。GWO优化的过程是通过连续计算ITAE值来评价该参数的质量，根据GWO的优化规则，通过连续迭代求出ITAE的最小值，从而得到一组分数阶模糊控制器的控制参数。

5 实验仿真

运用灰狼算法优化分数阶模糊控制器的参数，主要优化控制器参数α、Kp、Kd、Ki、Ku指标。在比较算法中，将按照各自算法最优的参数值进行设置，表1给出了算法的初始参数设置。

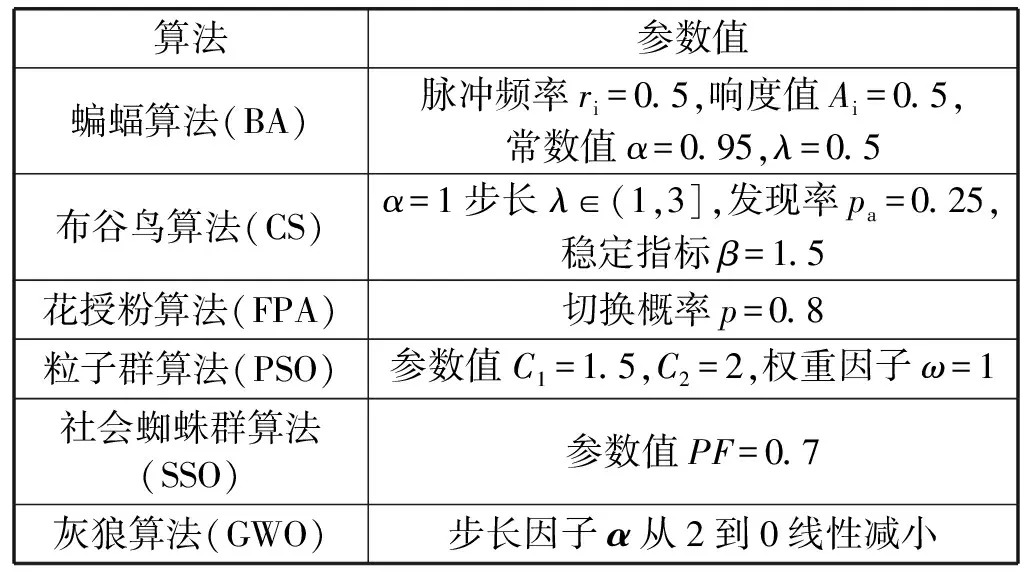
表1 算法的初始参数设置

在MATLAB R2012a上进行实验，且设置实验算法中统一种群规模为30，最大迭代次数为30次，独立运行次数为15次。为了验证分数阶PID模糊控制器的控制性能，采用隶属函数高阶系统对该控制器的性能进行测试，隶属函数高阶系统G(s)表示如下：

(22)

式中：s表示传递函数的复数域。

实验结果中高阶系统G(s)的ITAE表示最优值，表2展示不同算法测试隶属函数的最好值、最差值、平均值与方差值结果。

可以看出GWO在优化分数模糊控制器参数上获得较小的适应度值，而且测试隶属函数高阶系统G(s)，取得最小的误差。这说明GWO比SSO、PSO、FPA、CS和BA优化分数阶模糊控制器值获得较好的结果。

本文实验考虑到高阶动力系统的调节作用，将GWO优化分数阶模糊控制器的参数方法与蝙蝠算法、布谷鸟算法、花授粉算法、粒子群算法与社会蜘蛛群算法进行比较。响应时间设置为10 s，设置所有算法的种群数为30个，最大的迭代次数也设置为30次，独立实验次数为15次。表3展现了所有算法的优化分数阶模糊控制器的最佳参数值以及ITAE的平均值。结果表明，GWO与BA、CS、FPA、PSO和SSO相比具有更好的性能。

表3 优化算法校准模糊控制器G(s)最佳参数值

图3显示不同算法优化分数模糊控制器参数的收敛曲线，可以很明显看出GWO在优化分数阶问题获得较快的收敛速度，而且稳态误差也是最小的。图4展现高阶系统G(s)在不同算法所优化最佳参数值下的阶跃响应曲线，很明显在GWO优化分数模糊控制器参数下的隶属函数G(s)阶跃曲线有着更加平稳、超调量小、调节时间短、响应时间快等较好的动态性能。

图3 G(s)不同算法的收敛比较

6 结 语

本文提出一种基于灰狼算法的优化方法优化分数模糊控制器参数问题。GWO是一种新型的元启发式群智能算法，灵感来源于灰狼的捕食与社会等级等习性。该算法明确个体集中最优位置，避免因次优解的过早收敛、勘探与开采之间的不平衡关键缺陷。为了说明该算法优化参数问题的有效性与鲁棒性，针对高阶系统G(s)，通过GWO进行实验评价。为了评估GWO优化参数问题的性能，将该算法与蝙蝠算法、布谷鸟算法、花授粉算法、粒子群算法和社会蜘蛛群算法比较，实验结果表明，该方法在求解质量和收敛性方面优于其他方法。