基于曲线距离分析的嵌入式增强聚类算法
2021-10-18吴艳萍王红军李天瑞西南交通大学信息科学与技术学院四川成都611756
吴艳萍 王红军 李天瑞 邓 萍(西南交通大学信息科学与技术学院 四川 成都 611756)
0 引 言
随着互联网技术高速发展,降维技术和聚类技术已经在数据分析领域中被广泛使用。聚类是在没有任何先验知识的情况下,根据某种规则将数据分为不同的簇,同一簇内的样本相似度高,不同簇的样本相似度低[1]。聚类技术广泛应用于市场分析、医疗卫生、数据挖掘及金融投资等领域。降维是指利用某种映射规则将高维空间的数据映射到低维空间中[2]。高维数据对提取数据中隐藏的信息造成了很大不便,高维数据样本的某些特征对数据分析没有帮助,甚至干扰整个模型的性能。降维技术是处理高维数据、提升模型性能的有效手段,广泛应用于解决维度灾难问题[3-4],实现数据可视化[5-6]、特征选择[7-9]、消除数据冗余和降低模型噪声[10],可分为线性降维和非线性降维。其中线性降维技术更适用于维数相对较低的数据集,数据维度很高时则需要非线性降维技术。常见的线性降维技术有主成分分析(Principal Component Analysis,PCA)[11-12],旨在使降维后的数据在低维空间中数据的方差最大化,从而保留更多的数据信息。与传统的线性降维技术不同,等距特征映射(Isometric Feature Mapping,Isomap)是一种可以准确检测数据的潜在非线性结构并找到局部有意义的拓扑结构的经典非线性降维方法[13-14]。Isomap对有平坦的低维流形结构数据有很好的性能,而当数据以复杂不规则的形式组织时,其性能将会变差[15]。与Isomap相似,一种名为曲线距离分析(Curvilinear Distance Analysis,CDA)的基于曲线距离的降维方法被提出,CDA算法可以有效地检测到高维数据空间数据潜在的内在结构[16]。一般而言,对数据进行降维是为了提高后续数据处理的效率,如聚类或者分类。然而,传统数据分析的方法是先对数据进行降维,再对数据在投影空间进行后续的分析,其操作过程是顺序进行。而本文将聚类嵌入到降维算法中,使得聚类和降维操作同步完成。
本文提出一种基于CDA的嵌入式增强聚类算法(ECE-CDA),可以有效地将聚类算法嵌入到降维算法中,同步实现降维和聚类。本文算法是将聚类的目标与CDA的目标统一到一个整体框架之中,并且定义该框架的目标函数;应用凸优化方法求解目标函数最小值,目标函数取最小值时的降维和聚类结果即为最优的降维和聚类结果。在降维的过程中,CDA的思想使得数据点在高维空间中的相对曲线距离保持不变,而聚类的目标使得有可能划分为不同簇的数据点之间的界限清晰。最后在12个数据集上进行实验用以验证ECE-CDA性能。本文主要贡献如下:
(1) 简化数据分析过程,不需要任何额外的标签信息,将聚类嵌入到CDA算法中,使得聚类和降维以高准确率和低操作复杂度同步完成;
(2) ECE-CDA在保持高维数据的固有拓扑结构上性能优异,后续的数据分析方法可以高效地在投影空间执行;
微电网本质上是一种社区终端综合能源系统,是集成各种分布式能源和负载的能实现自我控制、保护和管理的小型发配电自治系统。社区能源系统如图1所示。
面对新时代基层统战工作发生的新变化,针对制约基层统战工作发展的主要因素,要始终坚持以习近平新时代中国特色社会主义思想、党的十九大精神,特别是习近平总书记关于加强和改进统一战线工作的重要思想为指导,以《条例》为根本遵循,进一步健全基层统战工作的机制体制,明晰基层统战工作职责,完善相应的刚性措施,夯实统战工作的基础保障。
(3) ECE-CDA可以作为同时实现聚类和降维的通用高精度框架。
1 相关工作
1.1 降 维
目前,已有许多高效的降维算法被广大学者所提出。如Wold等[17]早在1987年提出的主成分分析(PCA)选用数据的重要成分代替所有数据的特征,使得降维后的数据样本之间的方差最大化,从而保留数据信息。在此基础上,Schölkopf等[18]通过核函数将只能对数据进行线性降维的PCA算法改进为可以进行非线性降维的算法。Zhao等[19]提出了适用于大量二维图像的PCA算法,通过使用非均匀快速傅里叶变换,有效计算图像的膨胀系数,再将其与PCA相结合。Shashoa等[20]将线性判别分析(LDA)用于分类,提出了基于期望输出对线性分类器进行推导,并将推导结果应用到分类中的方法。
此外,非线性降维算法也深受广大研究者的青睐。如Roweis等[21]提出的流形学习算法局部线性嵌入(LLE),将其输入映射到较低维的单个全局坐标系中,并且其优化不涉及局部极小值。通过利用线性重构的局部对称性,LLE能够学习非线性流形的整体结构。此外,还有著名的多维标度法(MDS),其核心思想是在低维空间保留数据点在高维空间之间的相对距离。Rohde[22]解决了MDS在低维空间中数据点投影不连续的问题。Demartines等[15]在MDS的基础之上提出了曲线成分分析(CCA),该算法能展开强非线性甚至封闭的图形,其效率也大幅度提高。CCA使用欧氏距离衡量高维空间中数据点之间的成对距离,然而当样本的维度较高时,欧氏距离不能很好地衡量两个点之间的真实距离,因此Lee等[16]提出使用曲线距离计算数据点在高维空间中的成对距离,这种几何度量能更准确地检测嵌入在高维数据空间的低维流形结构。
本文中的ECE-CDA模型降维依赖于CDA的降维思想。首先,先对曲线距离分析算法进行介绍。CCA是一种非线性降维方式。假设有N个输入向量,每个向量为P维,即{xi|i=1,2,…,N},相应的输出向量为d维,即{yi|i=1,2,…,N}。CCA旨在将高维空间数据样本之间的距离关系映射到低维空间,其二次误差函数定义为:
(1)
式中:δij和yij分别是高维输入空间和低维输出空间的数据点i和j之间欧氏距离;F(yij)是关于yij的单调递减函数,其作用是在降维的过程中模型更加注重保持距离较近的数据点之间的距离。CDA是CCA的改进版本,用高维空间中任意两点的曲线距离代替任意两点之间的欧氏距离,因此当样本的特征个数较多时,曲线距离能更好地检测数据的流形结构。其目标函数为:
(2)
式中:xij是表示数据点i和数据点j在高维输入空间之间的曲线距离;yij是数据点i和数据点j在投影空间的欧氏距离;F(yij)为单调递减有界函数,用以保持样本点映射到低维空间的局部拓扑结构的不变性。
1.2 聚 类
聚类技术广泛应用于数据分析和数据挖掘领域,其目标是将相似的数据点尽可能分为同一簇。经典且广泛使用的聚类算法有很多种。如Bhargava等[23]在K均值的基础上提出了一种基于模糊C均值的混合聚类算法,用于数值和图像数据性能优化。Frey等[24]提出了一种全新的近邻传播聚类算法(Affinity Propagation,AP),该方法将原始数据点之间的相似性作为输入,在数据点之间传递实值信息,克服了传统方法选择随机选择出初始点而使聚类结果不佳的缺点。Rodriguez等[25]依据聚类中心点的密度比其他点的密度高,并且相邻的聚类中心点之间的距离较远的原理提出了密度峰值算法(Density Peaks,DP),该方法可以广泛应用于各个聚类场景。聚类算法的目标是最小化目标函数:
(3)
式中:k是类簇的个数;ys是属于第k个类簇的数据点;Ck是第k个类;ck是第k个类的聚类中心点;m是总的类簇数。
2 ECE-CDA模型设计
2.1 ECE-CDA模型目标函数
ECE-CDA模型将聚类嵌入到降维过程中,其目标是最小化损失函数,并得到聚类结果和数据点降维之后的坐标。其目标函数定义如下:
(4)
s.t. 0<α<1,0<β<1,yij≥0,xij≥0,∀i≠j
令:
(5)
(6)
式(5)中N是数据集的样本个数。式(6)中k是每一个类的索引,Ck表示第k个类,ck表示第k个类的聚类中心点,ys是属于第k个类的数据点,m是总的类簇数。α和β是两个权重因子,分别平衡E1(yij)和E2(ys)对目标函数的影响程度。考虑一个P维的输入数据X=(x1,x2,…,xN),X∈RN×p,再令Y=(y1,y2,…,yN),Y∈RN×d表示降维后的数据集。式(5)中的xij表示数据点i和数据点j在高维输入空间之间的曲线距离。文中使用Dijkstra[26]算法计算xij。令yij=d(yi,yj)表示数据点i和数据点j在低维投影空间之间的欧氏距离:
(7)

7.用式(16)或者式(20)更新聚类中心C;
(8)
式中:λy为常数。
2.2 ECE-CDA模型推理
针对式(4),本文的求解目标为降维之后的聚类结果和任意两点之间的距离,再根据全部样本的距离矩阵求解每个样本的坐标。式(4)是关于yij的凸函数,因此可采用批量梯度下降求解,可得其对应梯度为:
(9)
根据式(9),每更新数据点i和数据点j之间的成对距离,必须计算其他所有点的梯度和,即每更新迭代求解一个向量yi就必须考虑其他所有和向量yj(i≠j)相关向量影响的和,且更新后的值是距离,不是坐标。因此,根据随机梯度下降的思想,每次更新只与当前实例相关,即每次更新只更新某个具体实例。yj的更新方向沿着负梯度的方向进行,更新yj时yj对应的改变量为△yj≈-▽iE(yij,ys),其中▽iE(yij,ys)表示yj更新时E(yij,ys)对yj的梯度。E1(yij)可以表示为:
(10)
(11)
在数据集中依次选择向量yi,暂时固定yi,逐一遍历数据集中向量yj,∀j∈{{1,2,…,N}-{i}},然后每次使用随机梯度更新yj。选择yi之后,其他点yj在投影空间中的变化量即为梯度表示为:
△yj(i)=-αθ(t)▽jEij
(12)
式中:yj(i)表示当固定yi时yj的变化量。▽jEij是Eij对yj的导数;θ(t)是随迭代次数t变化的自适应学习率函数。本文定义θ(t)为:
(13)
计算▽jEij为:
(14)
(15)
根据式(12)、式(14)和式(15)可得:
(16)
式中:Nk是第k个类的样本个数;ys是属于第k个类的样本点。
13.returnY,L,C
(17)
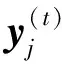
E2(ys)可以表示为另一种形式:
在施工过程中,通常会使用多种不同类型的临时施工构件,并需要通过Revit软件模拟施工,根据钢梁的实际分段情况将其分为不同的组别,支架使用长度和宽度均为1.0m的钻孔桩为基础,承重的立柱选择直径为600mm的钢管,2个横向钢管之间的分配梁均使用I56工字钢。安装拱柱时,应提前在钢箱拱的上端布置相应的支架,并在桥梁地面处设置长宽高分别为5m、6.5m、0.7m的支架。
(18)
聚类中心点ck可以由属于该簇的所有数据点决定,其计算式表示为:
(19)
为了达到降维过程中使用聚类引导降维,则需要求解每一次降维迭代中有可能属于同一类簇的点。则E(yij,ys)对ys的导数为:
在三门江林场中,为了使激励发挥其本质作用,真正的实现奖惩分明、奖勤罚懒,就必须制定合理的绩效考核制度,这也是所有企业对员工工作成果评价的重要一环。对员工的工作进行绩效考评,主要体现在两个方面,一个是对工作"量"的考评,一个是对工作"质"的考评。在绩效考核中,往往是综合这两方面来进行,若人力资源管理只关注某一方面,工作就会过于片面。绩效考核,需要对员工工作的优缺点进行客观系统的评价,通过科学合理的考核制度和考核办法,将每个员工的工作考评进行量化,得到一个最终成绩,依据此成绩,对员工的工作进行奖励和惩罚决定。
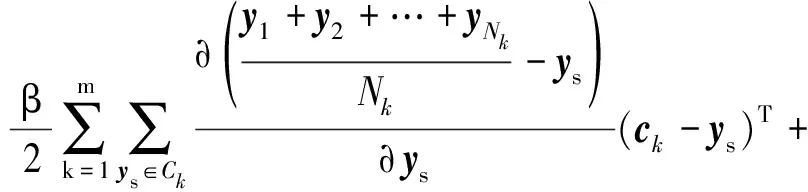
(20)
9.使用式(15)更新yj;
(21)
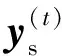
除了使用式(19)求解聚类中心点,也可以使用梯度下降求解聚类中心点,即:
但采尔在中研院的这段时间,蔡元培在上海医院疗养。但采尔多次致信问候蔡元培,也讲到他不适应南京气候,经常患肠疾,自己的病刚好,夫人又患类似的病,提出要提前回国。但采尔产生这个想法,除水土不服导致身体不适的原因外,更为重要的是当时上海战事不断,他怕近在咫尺的南京受到牵连,同时也为能否拿到月俸和返国费用而担心。
(3)在今后的研究中可以继续联合实地监测数据,除植被因素外,将景观要素和土壤要素以及周边居民满意度等要素,在生态重建效果评价中的重要性考虑进去。另外下一步工作中可以进一步结合多种评价方法,例如和层次分析法、灰色关联度法、聚类分析法、模糊综合评价法等做对比,对研究区的生态重建效果进行全面评价比较和分析。
(22)
根据式(22),聚类中心ck的迭代形式表示为:
(23)

2.3 算法描述
ECE-CDA模型算法流程如算法1所示。
算法1ECE-CDA算法
输入:X为一个N×p的数据集;d为低维投影空间的维度;m为类簇数;T为迭代次数。
目前国内外对于CKD-MBD疗效尚无统一判定标准,本次临床研究参照第三版《肾脏病学》[11](王海燕主编)、2013年中华医学会肾脏病学分会颁布的《慢性肾脏病矿物质和骨异常诊治指导》[8]及《中药新药临床研究指导原则》中“中药新药治疗慢性肾功能衰竭临床研究指导原则”[9]而制定。CKD-MBD疗效判定标准:显效:临床症状积分减少在60%及以上,且血清Ca、P、iPTH至少有两项在目标范围[12]之内。有效:临床症状积分减少在30%~60%,且血清Ca、P、iPTH只有一项在目标范围[12]之内。无效:临床症状积分减少在30%及以下,且血清Ca、P、iPTH均不在目标范围[12]之内。
输出:Y为一个N×d的数据集;聚类标签L;聚类中心C。
1.使用Dijkstra算法计算xij;
2.使用X矩阵的均值和方差初始化矩阵Y,在Y中随机选择m个向量作为初始化聚类中心C。
3.For 1:Tdo
4.计算投影空间数据点之间的相对欧氏距离;
5.计算C中的每个点到Y中其他点的距离,结果存入discp矩阵;
6.根据discp将Y中的数据点分为m个类簇;
F(yij,λy)取为单调递减的有界函数,其目的是在成对距离不能完全全部保持时,倾向于保持邻近的数据点之间的距离。
袁安皱着眉道:“以谷里师父学长们的本领,是可以将蚊子除掉的,宇晴师父种一片驱蚊的花花草草,比如艾蒿什么的,司徒先生做一批可以捉蚊子的木人,不是鼓捣他那个‘刑天’,药王他老人家配几缸药汁让聋哑村的仆役们洒扫,东方谷主再让大家练一练‘去势’剑法,三五天必有奇效。
8.使用式(14)计算yj;
根据随机梯度下降(SGD)的相关研究[27-28],使用SGD对损失函数求解最小值,则ys的迭代形式可以表示为:
10.使用式(19)更新ys;
11.将更新后的ys按原始顺序存入Y;
12.end for
在鸡的日粮中添加中药多糖,能显著提高鸡免疫法氏囊疫苗后的抗体水平和淋巴细胞增殖,在增强免疫功能方面表现出了很好的作用,其效果明显好于黄芪多糖,在临床应用上中药复方多糖效果也要好于单味多糖的效果.因此,中药复方多糖可作为免疫增强剂广泛应用于家禽的生产上,具有很好的研究价值与应用前景.
在为期4天的游学之旅中,游学队伍先后转辗河南省上蔡金丰公社、邵店分社、韩寨分社、小岳寺分社,河南省驿城金丰公社、和岗分社、程楼分社,河北省行唐金丰公社、伏流分社、上碑分社,3个金丰公社10个观摩点,辗转1000多公里,进行现场观摩学习,各分社社长现场讲解如何建组织配机械、如何发动农户、如何实现服务本村农户的过程和关键环节,各事业合伙人现场提问,边听边记,学之所长。
3 实 验
3.1 实验数据集
本文的实验在12个真实有效的来自于微软亚洲研究院多媒体[29](MSRA-MM)和UCI机器学习资料库[30]数据集上进行。公开访问的MSRA-MM由视频和图像数据集组成。其中图像数据集包含65 433幅图像,共有68个类别,每个类别大约包含1 000幅图像。本文选用其中8个数据集。UCI机器学习数据库目前大约包含488个数据集,本文选用其中4个数据集。数据集总结如表1所示。
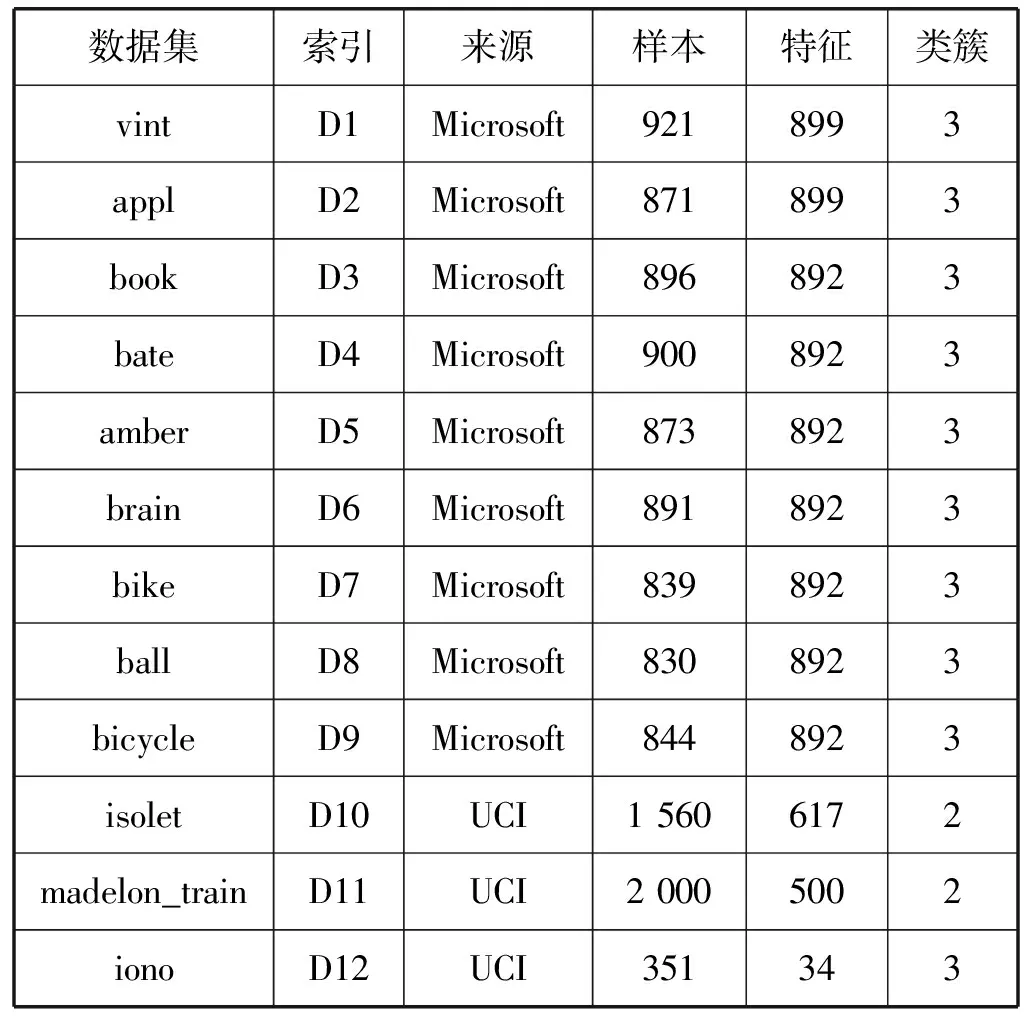
表1 实验数据集描述
3.2 评价指标
本节将详细阐述评价聚类和降维性能的度量标准。本文评价聚类和降维的性能均使用三种度量标准,即准确率[31]、纯度[32]、Friedman统计量[33]。准确率是根据实际的标签信息与模型预测的标签信息相对比而得到的比值。准确率指标计算式如下:
(24)
式中:k表示第k个类簇;m表示总的类簇数;ak表示第k个类簇中分类正确的样本数;N表示总的样本数。Acc的取值范围为[0,1],其中:Acc为0表示所有的样本分到错误的簇中去;Acc为1表示所有的样本都分到正确的类簇。
“机械工程材料基础B”是由上海理工大学机械工程学院开设的一门学科基础课程,授课对象是非材料类的学生,主要包括能源与动力学院和机械工程学院。这些学院的学生在今后学习专业课和进行科研工作的时候,不需要应用高深的材料学方面的知识,但却要掌握应用需要选择材料的方法和改进材料性能的手段,以及运用理论知识解释工程实际中的现象等。根据机械设计制造及其自动化专业工程认证的要求,按照“评价—反馈—改进”的质量监控和持续改进机制,以“机械工程材料基础B”的课程目标及其对毕业要求的支撑为依据,随机抽取该专业学生的考试结果进行分析和达成度计算,探讨改进教学质量的途径,培养符合工程认证要求的毕业生。
纯度计算式定义为:
(25)

通过把结构化与非结构化的信息数据统一格式、统一基准并空间化,导入到分布式文件系统HDFS中,导入完成后分布式文件系统自动触发档案内容提取流程,将办公文档、pdf、图片、视频等非结构化数据中的内容提取出来,按照特定的约束方式存到HBase构建的内容库中,同时将结构化数据发布到GIS服务集群中,供数据管理层提取和访问[3]。
本文使用Friedman统计量[33]全面评估ECE-CDA算法与其他对比算法之间的性能差异。Friedman统计是一种非参数测试的统计方法,使用该方法可以对比一组算法的性能差异。Friedman统计先将原始计算结果排序,即对不同算法在每个数据集上的准确率大小进行排序,性能最佳的为1,次优的排序为2,以此类推。基于排序的数值(rank值)、数据集个数和算法个数计算Friedman统计量,其定义如下:
(26)
通过计算FF对应的F分布,查表可计算其ρ值,通过该值可评估算法性能。
(27)
3.3 实验设置
本节详细介绍实验设置。首先,ECE-CDA模型的性能与多个影响因素有关,如参数的选择、迭代次数的选择及投影空间的维度等。投影空间维度的选择对ECE-CDA模型性能的影响尤为显著,一般来说投影空间维度越大,原始样本的信息保留程度就越好。为了公平进行实验对比,本文中投影空间的维度选择为原始样本维度的十分之一左右。经过参数调优选择,t0设置为0.5,α和β分别设置为0.7和0.3。
在推理上,两版教材的推理步骤以一步或两步为主.与美GMH版相比,浙教版的推理主要有两处:一是让学生通过平方运算求平方根,体会开平方与平方运算的互逆关系(见图9);二是无理数的引入,强化学生对有理数、无理数以及实数概念的辨别.总的来说,浙教版的推理水平对学生要求不高,只要求学生能掌握运算关系、概念等知识即可.
在实际应用场景中,ECE-CDA可以同时高效完成聚类和降维任务,因此在评价ECE-CDA的性能时,需要从降维和聚类两个方面分别进行评估。每个算法在每个数据集上执行10次,最终结果表示为精度为0.000 1的平均值。每个算法均使用准确率和纯度两种评价指标进行评估,最终使用Friedman统计量评估算法的综合性能。
本文将实验分为两组。第一组是综合评估ECE-CDA模型的聚类性能。本文选用的聚类对比算法为分别为用于聚类集成的基于暗知识的非负矩阵分解[34](NMFCE)、最小二乘均衡的平衡聚类[35](BCLS)、AP和DP。第二组是综合评估ECE-CDA模型的降维性能。由于无法直接知道降维后的数据保留了多少原始数据的信息,因此本文对降维算法降维后的低维数据均使用K-means进行聚类,结合聚类评价降维性能,用降维后的低维数据的聚类结果评估降维后的数据对原始数据集的信息保留程度,本文选用的降维对比算法为CDA、Isomap、CCA和PCA。
3.4 实验结果
1) 表2和表3是将ECE-CDA、NMFCE、BCLS、AP和DP分别应用于12个原始实验数据集的聚类结果,其中表2准确率后括号中的数值是将原始聚类准确率转换为rank值的结果,rank值代表不同算法在每个数据集上对准确率进行排序的序号。对于相同数据集的不同算法准确率和纯度的最大值被加粗显示。图1将各个聚类对比算法在各个数据集上的准确率与ECE-CDA算法进行对比。
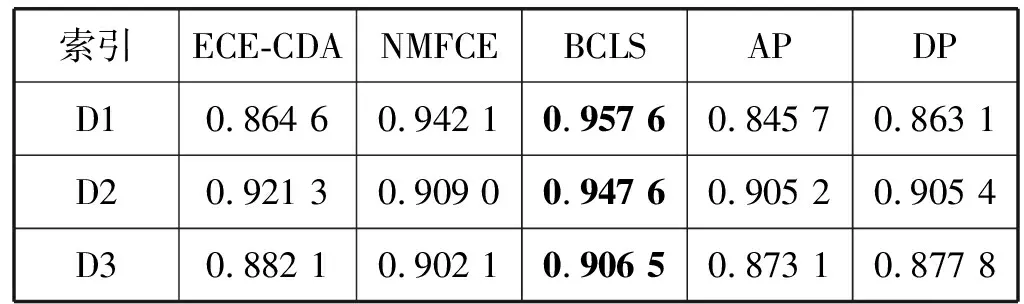
表3 ECE-CDA和聚类算法在原始数据集上的纯度对比

续表3
(1) 从聚类角度而言,ECE-CDA在大多数数据集上有更高的准确率和纯度值。如表2所示,ECE-CDA准确率分别在D1、D3、D4、D5、D7、D8、D9、D10、D11上取得了最大值,在超过四分之三的数据上ECE-CDA算法的准确度超过对比算法,而这四种对比算法仅在三个数据集上取得最优结果。如表3所示,ECE-CDA纯度在D5、D7、D9、D11、D12数据集上取得了最好的结果。ECE-CDA在12个实验数据集上取得了最高的平均准确率和最高平均纯度。由图1可以看出,ECE-CDA的准确率曲线在12个数据集上总体高于其他算法,这表明了ECE-CDA基于准确率这个评价指标其性能优异。由表2和表3可见,ECE-CDA在12个实验数据集上有最高的平均准确率0.502 5和平均纯度0.901 5。ECE-CDA的准确度分别比NMFCE、BCLS、AP和DP高4.93、9.60、12.35和5.86百分点。总体上,ECE-CDA在对数据进行聚类时,其性能明显优于本文所选择的对比算法。
(2) 基于Friedman统计测试对ECE-CDA聚类性能进行综合评价,ECE-CDA聚类性能相比于其他对比算法更优异。在表2中,ECE-CDA、NMFCE、BCLS、AP和DP在各个数据集上准确率的平均rank值分别为1.250 0、2.833 3、4.333 3、3.833 3和2.750 0。其中最优是ECE-CDA为1.250 0,第二为DP,第三为NMFCE,最后两位为AP和BCLS。Friedman统计量为:
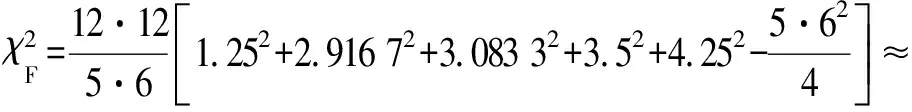
4.8·[1.562 5+8.027 6+18.777 5+14.694 2+7.562 5-45]≈
26.996 6
则Iman-Davenport为:
2) 本次实验5个算法,12个数据集,FF服从于自由度为5-1=4和(12-1)(5-1)=44的F分布。由F(4,44)分布计算的ρ值为1.70×10-7,所以在高显著性水平下拒绝原假设,即综合评价ECE-CDA算法聚类性能优于其他对比算法。
表4和表5是将CDA、Isomap、CCA和PCA分别应用于12个原始实验数据集的降维结果,其中表4准确率后括号中的数值是将原始降维准确率转换为rank值的结果,rank值代表不同算法在每个数据集上对准确率进行排序的序号。对于相同数据集的不同算法准确率和纯度的最大值被加粗显示。图2详细地将各个降维对比算法在各个数据集上的准确率与ECE-CDA算法进行对比。

表4 ECE-CDA和降维算法在降维后数据集上的准确率对比

表5 ECE-CDA和降维算法在降维后数据集上的纯度对比
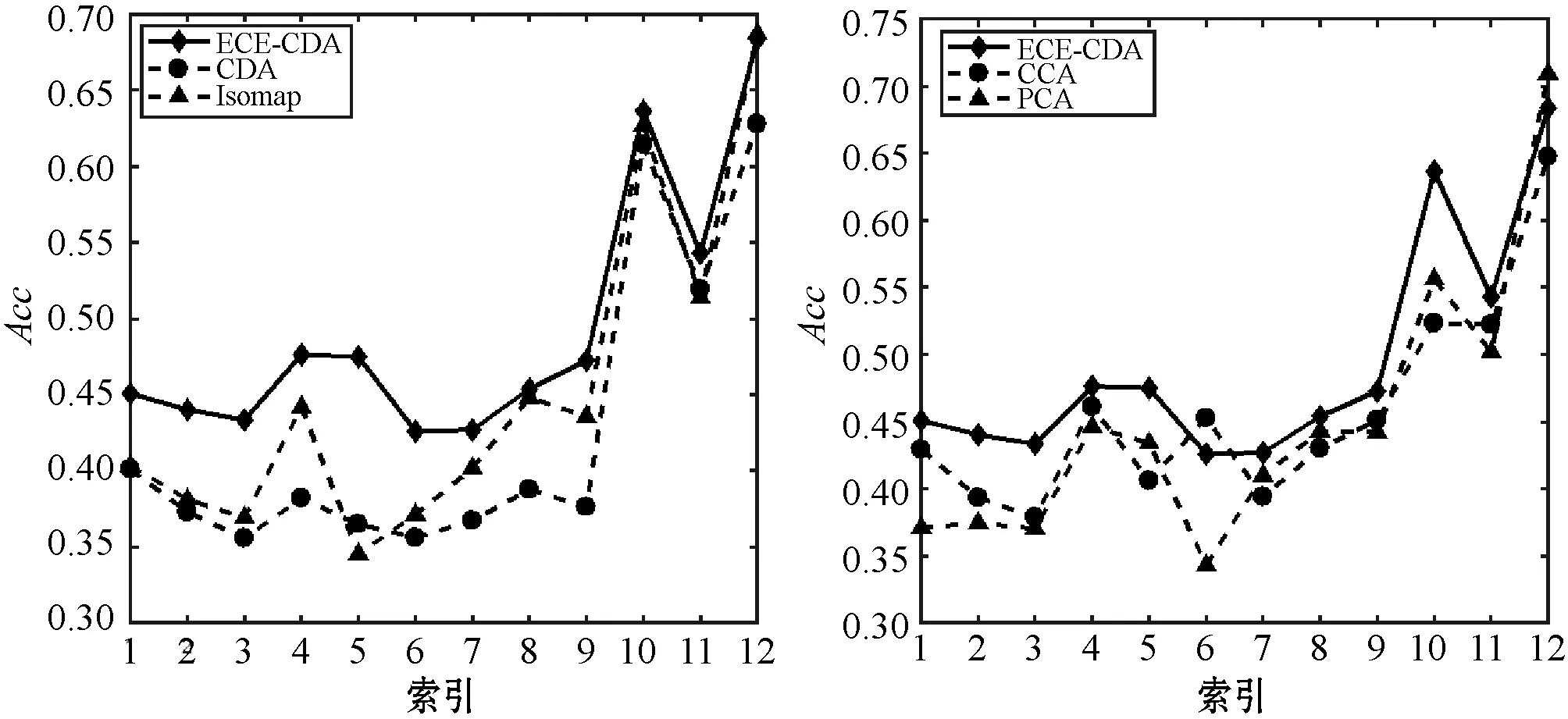
图2 ECE-CDA和对比算法在降维后数据集上 聚类准确率对比
(1) ECE-CDA与其他对比算法相比具有更高的准确率和纯度值。在表4中,ECE-CDA在12个数据集上取得了最大准确率,ECE-CDA在六分之五的数据集上,其降维性能优于CDA、Isomap、CCA和PCA。在表5中,ECE-CDA在8个数据集上相比于其他算法取得了最大纯度值。总之,ECE-CDA在12个数据集上准确率和准度均取得了最大值。由图2可以看出,ECE-CDA在12个数据集上有最高平均准确率0.493 2,分别比CDA、Isomap、CCA和PCA高6.61、4.10、3.58和4.30百分点。更多ECE-CDA降维性能的细节见表4、表5和图2。
(2) 基于Friedman统计测试对ECE-CDA降维性能进行综合评价,ECE-CDA降维性能相比于其他对比算法更优异。在表4中,ECE-CDA和CDA、Isomap、CCA和PCA在各个降维后数据集上的K-means准确率的平均rank值分别为1.250 0、4.416 7、3.250 0、2.750 0和3.333 3。其中最优是ECE-CDA,其他依次为CCA、Isomap、PCA和CDA。Friedman统计量为:
4.8·[1.562 5+19.507 2+10.562 5+7.562 5+11.110 9-45]≈
25.466 9
则Iman-Davenport为:
本次实验5个算法,12个数据集,FF服从于自由度为5-1=4和(12-1)(5-1)=44的F分布。由F(4,44)分布计算的ρ值为7.54×10-7,所以在高显著性水平下拒绝原假设,即综合评价ECE-CDA算法降维性能优于其他对比算法。
总之,ECE-CDA算法的性能达到了一个较高的水平,ECE-CDA在同时实现准确聚类和降维方面性能优异。
4 结 语
本文提出了一种基于曲线距离分析的嵌入式聚类算法ECE-CDA用于同时准确实现聚类和降维。与传统的方法不同,ECE-CDA将聚类过程嵌入在降维中,由聚类引导降维。ECE-CDA先使用Dijkstra算法计算数据点对在高维非线性空间的曲线距离,再构造权重函数保持局部拓扑结构不变性,最后在聚类的引导下将数据点之间的曲线距离投影至低维空间。ECE-CDA模型可看作一个通用的高精度框架,即用于实现同时聚类和降维。实验结果表明所提出的ECE-CDA算法在降维和聚类上性能优异,其正确性和可行性都较高,有广泛的应用场景。
受算法设计影响,本文每一次更新迭代都需要计算成对距离矩阵。未来将致力于研究迭代求解算法的大矩阵计算的相关问题,并引入更多的数据信息,进一步提高算法的计算速度和结果的准确度。
