基于MEMS IMU和运动约束的共享单车定位算法

牛小骥, 丁龙阳, 旷 俭, 吴宜斌

(1. 武汉大学 卫星导航定位技术研究中心，武汉 430079；2. 武汉大学 测绘学院，武汉 430079）

共享单车作为一种新型绿色环保的出行工具，近些年已经深入到人们的日常生活中。高精度高可靠性的单车定位系统对于提升用户体验，减少运营成本至关重要。目前共享单车所依靠的主流定位手段是全球卫星导航系统（Global Navigation Satellite System, GNSS），但是GNSS 在城市峡谷、隧道等场景中，因为信号遮挡和多路径等因素的影响，定位精度会迅速下降甚至完全失效。因此亟需一种价格低廉、连续可靠、易于推广的单车定位方案用于弥补当前GNSS 定位的不足。

微机电系统（Micro-Electro-Mechanical System, MEMS）惯性测量单元（Inertial Measurement Unit, IMU）因为尺寸小巧、成本低廉且不受外界环境干扰，被广泛应用在各种要求连续可靠的定位场景中。但是基于MEMS IMU 的惯性导航系统（Inertial Navigation System, INS）因为传感器噪声和零偏误差等影响，定位误差会随着时间迅速积累[1]，很快就超出共享单车定位误差的容许范围，因此需要寻求辅助信息来抑制其误差发散。

对于地面轮式载体，里程计（Odometer, ODO）是一类重要的辅助传感器[2]。车载导航中常采用里程计提供的速度或距离信息与INS 组合（ODO/INS）作为GNSS 定位的补充，在GNSS 失效的环境下提供稳定连续的定位结果[3-5]。但ODO/INS 组合方案需要增加额外的车轮编码器，增加了成本和系统复杂度，无法满足目前共享单车定位系统对于低成本以及可推广性的迫切需求。

地面轮式载体一般满足非完整性约束（Non-Holonomic Constraints, NHC），即在不打滑、不腾空的情况下，载体横向和垂向的速度为零[2]。该运动约束作为地面轮式载体的固有特性，也常用作辅助信息抑制INS 误差的累积[6]。文献[7]将NHC 和里程计结合使用用于车载导航，有效抑制了INS 误差的发散，提高了系统稳定性。文献[8][9]将IMU 安装在车轮中心与车轮一起旋转，通过陀螺测量值与车轮半径得到载体运动速度，并结合NHC 构造三维速度信息。

上述有关非完整性约束用于导航定位的研究主要集中在车载导航或轮式机器人导航，用于自行车这类两轮载体的较少，主要是顾虑于骑行过程中的左右晃动对NHC 的破坏。文献[10]基于骑行者的运动模型设计了一套用在骑行者所携带设备上的航位推算（Cycling Dead Reckoning, CDR）算法，但也无法解决目前共享单车定位存在的问题。针对上述问题，本文设计并实现了一套融合INS 和非完整性约束的单车定位算法（NHC/INS），并着重探讨了安装角误差和杆臂补偿对NHC 使用效果的影响。

1 单车定位算法

1.1 算法框架

图1 展示了本文设计的共享单车定位算法流程：首先通过惯导机械编排获得IMU 的位置、速度和姿态。然后将GNSS 解算位置、INS 推算结果以及NHC约束信息通过扩展卡尔曼滤波（Extended Kalman Filter, EKF）进行数据融合得到修正后的载体位姿。在GNSS 信号中断时，仅利用NHC 修正INS 误差（即NHC/INS 方案）。

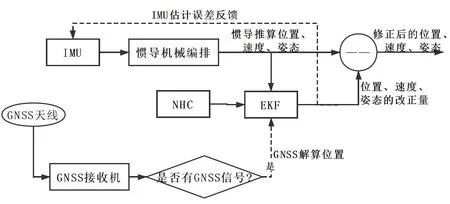
图1 单车定位算法框架Fig.1 Architecture of the proposed bicycle positioning algorithm

1.2 IMU 安装方式与坐标系定义

本文算法涉及到的坐标系包括导航坐标系（n系），IMU 坐标系（b 系）和载体坐标系（v 系）。具体地，本文采用北-东-地（NED）轴线定义的当地水平坐标系作为导航坐标系，其原点选在载体上的某一参考点，其z 轴与该点大地参考椭球的法线重合并指向地心，x 轴与子午线重合并指向北极，三轴构成右手坐标系。IMU 坐标系的原点位于IMU 的测量中心，各个坐标轴分别平行于IMU 的三个敏感轴，构成右手坐标系。载体坐标系的坐标原点选在自行车后轮与地面的接触点，x 轴沿后轮前进方向，y 轴垂直后轮平面指向载体右侧，z 轴垂直向下，与x、y 轴共同构成右手坐标系（如图2 所示）。

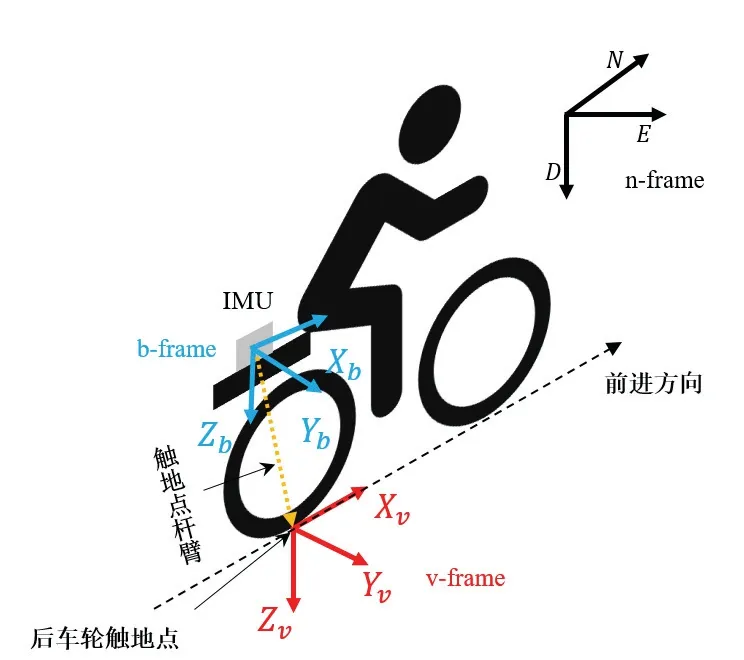
图2 IMU 安装方式与相关坐标系定义Fig.2 Installation scheme of the MEMS IMU and the definitions of the vehicle frame(v), IMU body frame(b) and navigation frame(n)

本文将IMU 安装在自行车后座上。惯导机械编排推算得到IMU 自己的导航状态，而NHC 约束的是载体坐标系下的载体速度，因此融合NHC 和INS 需要已知两个坐标系（IMU 坐标系和载体坐标系）之间的相对关系。而在实际系统中，不可避免地会存在安装误差，包括安装角和杆臂。安装角指的是IMU 坐标系（b 系）与载体坐标系（v 系）因轴系不平行所引起的差异；杆臂在这里指的是IMU 测量中心与载体速度投影中心之间的相对位置关系。值得注意的是，自行车不同于四轮载体，在骑行过程中为保持平衡而难免发生左右晃动，因此NHC 在自行车车身处并不严格成立，但在车轮触地点却是成立的。因此本文选择后车轮触地点作为载体速度投影中心来融合NHC 和INS，并定义杆臂为IMU 测量中心到后车轮触地点的向量。IMU 安装位置以及安装角和触地点杆臂的定义如图2所示。

1.3 系统误差状态模型

带有辅助信息的惯性导航常采用误差状态卡尔曼滤波（间接卡尔曼滤波）进行组合导航解算，以解决系统的非线性问题[11]。本算法采用21 维误差状态向量，包括导航状态向量与IMU 误差向量，即：

陀螺和加速度计零偏以及比例因子均建模为一阶高斯-马尔可夫过程[2]：

其中 Tgb、 Tab、 Tgs、 Tas分别为陀螺零偏、加速度计零偏、陀螺比例因子以及加速度计比例因子的相关时间，wgb、wab、wgs、was为对应的驱动白噪声。

1.4 车轮触地点零速约束模型

对于一般轮式载体，如汽车或者轮式机器人，当其正常行驶时（不发生侧滑和跳跃）只有沿前进方向的速度，侧向和垂向速度为零，这一基本假设被称为非完整性约束（NHC）。但不同于汽车或轮式机器人，自行车骑行过程中为了保持平衡而不得不发生或大或小的左右晃动，因此NHC 在自行车车身处并不总是成立。但对于车轮着地点而言，只要车轮不发生侧滑或垂向跳跃，该点处的非完整性约束是严格成立的。因此本文将IMU 测量中心的速度通过安装角和杆臂投影到后轮着地点处，利用其侧向和垂向速度为零进行约束。在载体坐标系下，当非完整性约束成立时，速度观测向量可以表示为：

vv表示载体沿前进方向的速度； ev表示观测噪声，其方差参数可以根据载体的运动状态初步给定，并通过残差进行调整。由IMU 推算得到的速度投影到自行车后轮触地点可以表示为：

本算法只对侧向速度和垂向速度进行约束，因此上述观测方程只取侧向与垂向分量。

2 实验描述

为验证本文所设计的NHC/INS 组合导航算法的定位精度，并与传统INS 方案进行对比，本文在开阔的马路上进行了实测验证。实验设备及安装情况如图3 所示。本文采用了武汉大学卫星导航定位技术研究中心自主研发的GNSS/INS 组合导航模块INS-Probe，并安装了HX-CSX601A 测量型天线用于收集GNSS数据。INS-Probe内置的MEMS IMU型号为InvenSense公司的ICM20602，主要技术参数如表1 所示。INS-Probe 被安装在车轮后座并使其尽可能与车轮平行。车轮触地点杆臂通过卷尺多次测量取平均值得到，安装角采用文献[12]提出的方法估计得到。实验数据的处理方式均为实时采集模式下的事后处理。

表1 被测MEMS IMU(ICM20602)技术参数Tab.1 Technical parameters of the MEMS IMU (ICM20602) used in the tests

图3 实验数据采集设备Fig.3 Experimental platform.

为比较不同骑行动态下安装角误差和杆臂补偿给NHC/INS 定位性能带来的影响，本文进行了两组实验。一组实验为正常骑行，自行车左右晃动幅度较小；另一组实验为“S 形”骑行，自行车左右晃动幅度较大。两组实验的自行车倾角变化如图4 所示。实验1 自行车平均速度为2.2 m/s，实验2 自行车平均速度为2.9 m/s，两组实验骑行时间均在30 min 左右。

图4 自行车倾角变化Fig.4 Lean angle of the bicycle in the two tests

本文实验的位置参考真值采用事后动态差分（Post Processed Kinematic, PPK）与INS 松组合的结果，其中PPK 全部为固定解，参考真值精度可达厘米级。为了评估本文设计的NHC/INS 共享单车定位算法的性能，本文采用模拟GNSS 中断的方式进行实验分析。通过融合GNSS 定位信息，在MEMS IMU 误差充分收敛后，周期性地模拟GNSS 数据中断60 s，每次中断之间恢复GNSS 数据60 s 使惯导误差重新收敛。每组实验共中断10 次，并统计每次中断定位误差最大值的RMS 值作为统计结果。对比实验结果分析具体分为以下三个方面：

1) 对比纯惯导推算与加入NHC 后的位置误差漂移；

2) 对比不同骑行动态下安装角误差对本文NHC/INS 算法性能的影响；

3) 对比不同骑行动态下杆臂补偿对本文NHC/INS算法性能的影响。

3 实验结果与分析

3.1 INS 方案与NHC/INS 方案对比

图5 为实验1（正常骑行）在10 次模拟中断GNSS信号60 s 条件下得到的两种方案的定位轨迹对比图。统计正常骑行时（实验1）每次中断误差漂移最大值的RMS 值作为位置误差，结果如表2 所示。此时对IMU 安装角误差和杆臂都进行了补偿。

表2 正常骑行时GNSS 中断60 s 位置误差统计（RMS 值）Tab.2 Position error statistics (RMS) during 60 s GNSS outages in test 1

图5 模拟10 次GNSS 中断60s 条件下定位轨迹对比。其中红色表示参考真值轨迹，蓝色表示INS 方案推算轨迹，绿色表示本文NHC/INS 方案推算轨迹。Fig.5 Estimated trajectories of different schemes in the 10 sets of 60s GNSS outage experiments. The red represents the ground truth; the blue represents the trajectory estimated by INS; the green represents the trajectory estimated by the NHC/INS scheme proposed in this paper

结果显示，纯惯导推算在GNSS 中断条件下，由于没有任何的约束信息，误差发散很快，在1 min 后其水平方向和垂直方向的位置漂移分别达到了20 m和4 m 左右。当正确加入NHC 约束修正后，三个方向的定位精度分别提升了91%、95%和83%。此外，在NHC/INS 方案中，北向位置误差发散相较于东向和垂向更大，这是因为NHC 无法对前向速度进行约束，而本文实验轨迹的主要前进方向为南北方向。

为进一步评估NHC/INS 方案在极端情况下的定位性能，对实验1（正常骑行）模拟5 次GNSS 中断5 min 的场景，每次中断相互独立，统计5 次中断下误差漂移最大值的RMS 值，绘制误差漂移曲线如图6(b)所示。图6(a)为纯INS 方案对应的位置误差漂移曲线。

图6 位置误差漂移曲线Fig.6 Position drift errors of the two navigation schemes.

根据图6 可以看到在中断GNSS 信号5 min 的苛刻条件下，INS 方案的水平位置误差统计值会达到千米量级；而当正确加入NHC 后，北向和东向定位误差统计值只有4.0 m 和2.5 m。此外，NHC/INS 方案的误差曲线中北向和东向误差并不是一直发散，而是发散与持平相间出现。这是因为本文实验轨迹中存在周期性的掉头，而惯导位置误差的一些影响因素（如航向误差）是与此相关的，这样会导致水平方向的误差漂移方向被逆转，误差不再沿一个方向持续累积。同时，曲线统计的是GNSS 中断期间误差漂移最大值的RMS 值，故会出现一段局部持平的状态。此外，由于高程方向的这种轨迹方向变化带来误差漂移方向明显逆转的作用不强，故而呈现出持续发散的趋势。

在实际GNSS 信号遮挡严重的环境中，只依赖MEMS IMU推算所带来的几百米甚至超过1公里的定位误差对于共享单车的管理而言显然是难以接受的。而当正确加入NHC 后（即有效补偿IMU 安装角和杆臂影响后），不需要增加任何额外的硬件成本便可以保证较高的定位精度，从而为共享单车在复杂场景下的定位难题提供了一套可行的解决方案。下文通过实验数据的对比处理来探讨在不同骑行动态下IMU 安装角误差与杆臂补偿对NHC 修正效果的影响。

3.2 安装角误差对NHC/INS 定位性能影响

本文实验采用文献[12]提出的方法估计得到的航向安装角为-0.649 °，俯仰安装角为-1.449 °（横滚安装角不可估，对于NHC 也不需要）。表3 展示了两组实验中，补偿与不补偿安装角的条件下NHC/INS 定位算法在模拟中断GNSS 信号60 s 条件下的位置漂移误差的统计结果。图7(a)-(d)为两组实验在补偿安装角前后，车轮触地点在载体坐标系下的速度投影图。

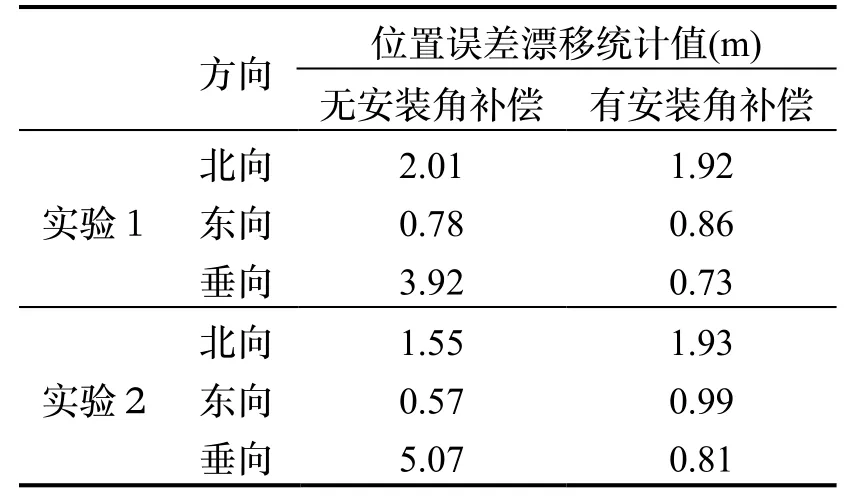
表3 IMU 安装角补偿对自行车NHC/INS 定位性能影响Tab.3 Effect of mounting angles compensation on the performance of NHC/INS

结果显示两组实验在补偿安装角前后其平面方向的位置精度差异不大，这是因为在安装角中影响水平位置精度的主要是航向轴，而本实验中航向安装角较小(-0.649°)，所以从统计结果来看，补偿安装角前后对水平方向的定位精度影响不大，补偿前后在同一个数量级。但是，经安装角补偿后，高程方向精度提升明显，其中实验1 的垂向误差从3.92 m 减小至0.73 m，实验2 的垂向误差从5.07 m 减小至0.81 m。这是因为在将IMU 速度从b 系投影到v 系的过程中，俯仰安装角主要影响的是垂直方向的速度。如图7 所示，补偿安装角之后，两组实验在载体坐标系（v 系）中的垂向速度投影均明显减小，更严格地符合NHC 约束。

图7 安装角补偿前后的速度投影Fig.7 Vehicle velocity in the vehicle frame before and after mounting angles compensation

具体可解释为，在只考虑俯仰安装角时，从b 系转换到v 系的方向余弦矩阵Cvb可以表示为：

由于只有前向速度 vx较大，故俯仰安装角对补偿前后的垂向速度影响更大。

3.3 杆臂补偿对NHC/INS 定位性能影响

本文实验对IMU 杆臂进行多次测量得到的平均值为（-0.053 m，0.001 m，0.730 m）。表4 展示了两组实验（正常骑行和“S”形骑行）中，补偿与不补偿杆臂的条件下NHC/INS 定位算法在中断GNSS 信号60s条件下的位置误差统计结果。图8(c)与图8(d)分别为两组实验在不进行杆臂补偿时，车轮触地点在载体坐标系下的速度投影。

表4 杆臂补偿对自行车NHC 性能的影响Tab.4 Effect of lever-arm compensation on the performance of NHC/INS

从表格数据可以看出，补偿杆臂前后垂向误差变化不大；东向位置精度在补偿杆臂后提升较大；而北向位置精度提升非常显著。同时从结果可以看出，杆臂补偿对于实验2 的影响要明显大于实验1。这是因为不进行杆臂补偿时，NHC 约束的是车轮后座IMU处的速度，而实验2 自行车的左右晃动幅度更大，此时杆臂对速度投影的精度和稳定性影响更大（如图8(d)）。从图8(c)-(d)中可以看到，实验2 不补偿杆臂时，侧向速度投影明显增大。因此这种情况（自行车动态较大）下，杆臂补偿带来的性能提升更为明显。

图8 杆臂补偿前后的速度投影Fig.8 Vehicle velocity in the vehicle frame before and after lever-arm compensation

此外，从统计结果来看，南北方向作为自行车轨迹的主要前进方向，其受杆臂补偿的影响要明显大于东向和垂向，这与文献[13]的实验结果是一致的。这是因为当不进行杆臂补偿的时候，NHC 约束的是自行车后座的速度，该处的垂向和侧向速度实际上并不为零，然而NHC 却以较高的置信度认为该点垂向和侧向速度为零，那么算法就会将这一矛盾不恰当地归咎到前向上，从而造成前向位置误差增大，在本文实验中则主要表现为南北方向的位置误差。

4 结 论

本文针对当前共享单车在城市复杂场景下难以实现连续精准定位的问题，设计并实现了一套基于MEMS IMU 与车轮触地点非完整性约束（NHC）的定位算法。相比于传统纯惯导推算（INS 方案），本文所设计的NHC/INS 融合定位方案在GNSS 中断60s 条件下，“北-东-地”三个方向的定位精度分别提升了91%、95%和83%。在模拟GNSS 中断5 min 的极端情况下，NHC/INS 方案在“北-东-地”三个方向的定位误差最大值的RMS 统计值也仅为4.0 m、2.5 m 和4.0 m，可以满足共享单车日常管理对定位精度的需求。此外，本文还重点探讨了IMU 安装角误差与杆臂补偿对自行车NHC 修正性能的影响。定量对比结果表明，忽略安装角或杆臂补偿都会严重影响NHC 约束作用的发挥，显著降低定位精度。

本算法未对自行车前向速度进行约束，因此后续可以考虑以下研究方向：一是根据自行车本身的平衡特性构建约束信息，进一步抑制前向定位误差的发散；二是考虑将IMU 安装在车轮上与之一同旋转，起到里程计的作用，从而约束前向速度误差，进一步提高定位精度和可靠性。