锚杆组合构件预应力传递效应的解析计算

蒋 威，瞿 浩，石 蒙，王东攀

（1.中国矿业大学（北京）资源与安全工程学院，北京 100083；2.天地科技股份有限公司 开采设计事业部，北京 100013；3.伊金霍洛旗呼氏煤炭有限责任公司 淖尔壕煤矿，内蒙古 鄂尔多斯 017200）

组合锚杆支护技术在我国大部分煤矿推广应用，成为现代矿井首选的、安全高效的巷道支护方式[1-3]。常见组合构件有钢带和钢梁，能够显著增加锚杆支护的适应性和支护效果[4-5]。近年来，为了适应深部、复杂条件开采巷道难支护的问题，在组合支护的基础上，康红普等学者提出了高预应力强力支护理论[6-9]，强调了预应力在巷道支护中的重要性，工程应用效果良好[10-12]。关于预应力的作用机理及其与锚杆组合构件的作用关系，国内学者进行了较多研究。李冲，徐金海等人采用理论分析、现场实测等研究方法，得到了锚杆杆体轴应力、剪应力与预紧力的关系以及杆体轴应力与剪应力的分布规律[13]；康红普，吴拥政等人分析了组合构件在锚杆支护过程中的作用，使用有限元数值模拟计算了W钢带在预应力影响下的应力分布和变形特征[14]；对于预应力的分布特征，康红普等人通过数值模拟对比分析了不同支护形式下锚杆预应力的应力场分布，得到了一些规律[15]。不过，在组合构件影响下，锚杆预应力在围岩中的分布规律，国内研究较少。弹性地基梁理论在计算过程中同时考虑了梁和地基的变形，以其较高的计算精度，在工程领域中广泛应用[16-18]。在预应力组合锚杆支护中，组合构件起到了地基梁的作用，预应力则通过组合构件传递到围岩（地基）中[19-21]。所以，在计算预应力分布的问题中，弹性地基梁理论较为契合。为此，通过建立一般锚杆组合构件支护顶板的弹性地基梁模型，求解地基梁的挠曲方程，以得到预应力通过组合构件传递到围岩中的理论分布，并分析其分布规律的影响因素，对于巷道支护构件选材、锚杆布置方式具有指导意义。

1 锚杆组合构件作用机理及其弹性地基梁模型

1.1 锚杆组合构件作用机理

在井巷施工中，通常在锚杆与围岩之间布置钢带（平钢带、W钢带或M钢带），形成组合支护。钢带与围岩接触面积较大，可以将锚杆的预应力荷载分散的传递到围岩，扩大锚杆作用范围。此外，钢带可以将多根锚杆连接在一起，使其协同作用于围岩，共同形成组合支护系统，提高支护系统的整体刚度与支护能力[22-23]。

1.2 锚杆组合构件的弹性地基梁模型

取矩形巷道中顶板的锚杆组合支护为例。为方便计算，锚杆组合构件选用平钢带，其上组合布置3个预应力锚杆，并忽略托板等构件的影响。假设顶板符合Winkler地基假设[24]（地基表面任一点的沉降与该点单位面积上所受压力成正比），则弹性地基梁模型以顶板为地基，以钢带为弹性地基梁，3个预应力锚杆简化为在弹性地基梁不同位置分别作用的3个集中力。顶板支护的弹性地基梁模型如图1。

如图1，以钢带一端为原点O，另一端为x轴正方向，预应力作用下的钢带经简化后可以定性为两端为自由端，受3个集中力p（分别与原点距离为a，b，c）作用的弹性地基梁。在集中力作用下，弹性地基梁（钢带）与地基（顶板）协同变形，结合Winkler地基假设，则顶板的地基反力pc与钢带的铅垂位移（挠度）z（x）的关系为：

图1 顶板支护的弹性地基梁模型Fig.1 Elastic foundation beam model of roof support

式中：kc为顶板的地基系数，即使顶板产生单位沉陷所需的压强；bv为钢带的厚度。

顶板的地基反力pc的分布曲线，即为锚杆预应力经钢带传递后在顶板中的分布曲线。为得到该分布曲线的解析解，对图1中的弹性地基梁模型展开计算。

2 模型的计算

2.1 地基梁类型划分

考虑到梁的端部效应，根据地基梁特征长度L的不同，弹性地基梁可分为无限长梁、半无限长梁以及短梁，3种梁的划分标准为如下：

1）无限长梁。荷载和两端的距离都大于3L。

2）半无限长梁。荷载与一端的距离小于3L，与另一端的距离大于3L。

3）短梁。荷载与两端的距离都小于3L。

为了提高计算效率，并保证计算结果的准确性，在计算开始之前，应根据特征长度L值以及荷载的位置，确定地基梁的类型，以决定能否忽略端部效应，从而选择更合理的解析方法。

式中：E为钢带的弹性模量；I为钢带的惯性矩，I=wbv3/12；w为钢带的宽度。

钢带的材质一般为铸钢，铸钢弹性模量E为200 GPa左右，普通软岩（煤）的地基系数kc为0.06×106～0.12×106，取钢带宽度w为250 mm，厚度bv为5 mm，则地基梁特征长度L的取值范围为1.365～1.623 m，则3L=4.095～4.869 m。根据一般工程经验，锚杆与钢带两端的距离均小于3L。因此，钢带的计算属于短梁问题，应考虑端部效应，采用初参数法进行计算。

2.2 地基梁的挠曲方程建立

初参数法即使用初始截面O的4个参数挠度z0、转角θ0、弯矩M0、剪力Q0来表示梁的挠度方程。其优点是可以使积分常数具有明确的物理意义，且可以根据参数的物理意义寻求简化的途径。

当短梁上除地基反力外，仅受1个距端点为a的集中力p作用时，其挠曲方程为：

式中：β为此弹性地基梁的变形协调系数。

准1（βx）、准2（βx）、准3（βx）、准4（βx）为克雷洛夫函数[20]，表示如下：

式中：。

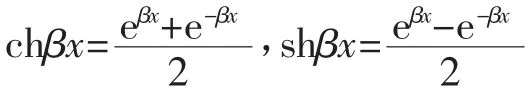
由叠加原理可知，当在距离原点为b和c 2处再加2个集中力时（图1），仅需在式（3）再加入2个挠度修正项：

上2式分别为x>b和x>c时应加的修正项。

2.3 边界条件及求解

在得到地基梁的一般方程后，应根据其边界条件进一步确定4个初参数z0、θ0、M0、Q0的值。

由梁的两端为自由端可得：

弯矩M和剪力Q的方程式可通过下式求得：

结合式（5）和式（7）即可得到弯矩M和剪力Q的方程式，再将式（6）代入其中即可求得4个初参数的值。省略计算过程，结果如下：

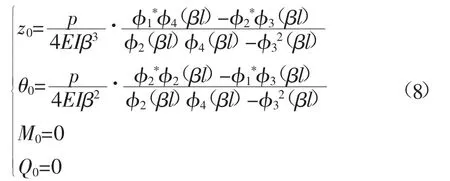
式中：准1*、准2*为中间转换变量。

准1*=准1（β（l－a））＋准1（β（l－b））＋准1（β（l－c））

准2*=准2（β（l－a））＋准2（β（l－b））＋准2（β（l－c））

2.4 挠曲方程的演绎

由上面的计算过程可知，在其他参数不变的条件下，集中力的增加仅会造成挠曲方程中相应挠度修正项的增加以及准1*和准2*的改变。因此，假设钢带上有n个预应力锚杆，作用力均为p，锚杆的位置分别对应x1、x2、…、xn，此时钢带的弹性地基梁挠曲方程为：

式中：准n1*、准n2*为中间转换变量。

准n1*=准1（β（l－x1））＋准1（β（l－x2））＋…＋准1（β（l－xn））

准n2*=准2（β（l－x1））＋准2（β（l－x2））＋…＋准2（β（l－xn））

3 顶板地基反力分布特征

3.1 地基反力影响因素

在确定钢带的挠曲方程之后，结合式（1）、式（4）和式（9），即可得到受n个不同位置集中力作用时地基反力的分布方程，亦即n个不同位置预应力锚杆作用在钢带上时，顶板的地基反力pc分布方程。

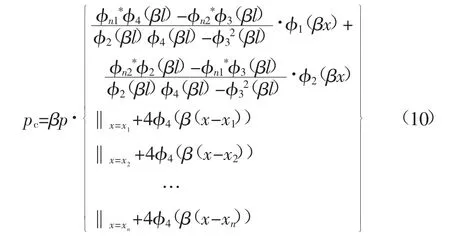
3.1.1 变形协调系数β

由式（10）可以看出，变形协调系数β是影响顶板地基反力分布的重要参数。而且，β可以表征钢带的抗弯刚度EI以及顶板的地基系数kc等参数对地基反力分布的影响，具有较大意义。

结合前文中的一般工程参数，由式（4）计算可得β的一般值约为0.7。为分析变形协调系数β对顶板受力分布特征的影响，分别计算β=0.7、1.4以及2.1时钢带中部受单根锚杆作用的顶板的地基反力pc1、pc2、pc3分布。计算结果为：

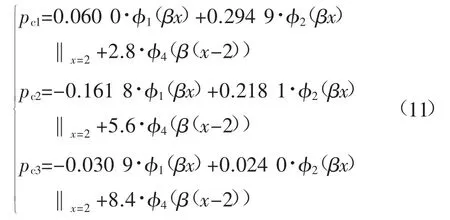
如此得到的不同变形协调系数条件下顶板的地基反力分布如图2。

图2 不同变形协调系数时顶板地基反力分布图Fig.2 Distribution of the roof reaction force with different deformation coordination coefficients

由图2可以得出，地基反力pc在预应力作用点（x=2）达到峰值，在作用点两边对称分布且随着远离作用点逐渐减小。随着变形协调系数β值的增大，地基反力的峰值逐渐增加，作用点两边地基反力的衰减幅度也相应增加。在钢带两边地基反力小于0表示钢带在中部受力的情况下，两端翘起，脱离顶板。综合来看，变形协调系数β值越小，地基反力分布越均匀。

结合式（4）来看，变形协调系数β与地基系数kc正相关，与钢带抗弯刚度EI负相关。岩层越软（地基系数越小），预应力传递越均匀，故预应力锚杆在软岩支护中更能发挥效力；提高钢带的抗弯刚度可以促进预应力均匀传递，加强支护效果。

3.1.2 端部效应

前文提到，钢带的计算属于短梁问题。因此，钢带的端部效应，对地基反力的分布亦有较大影响。省略计算过程，单根锚杆作用在4 m长钢带时，随着锚杆作用位置由钢带端部移向钢带中部，顶板的地基反力分布曲线如图3。由如图3可知，当锚杆预应力作用点x=100 mm时，在钢带近端端点引起的地基反力最大pcmax=1.32p，随着靠近远端，该预应力引起的地基反力不断降低，在远端端点引起的地基反力最小pcmin=-0.21p；随着预应力作用点不断内移，地基反力分布曲线逐渐由上凹变为下凹；当锚杆力作用在钢带中部x=2 000 mm时，地基反力在作用点两边对称分布，最大地基反力为0.38p；此外，作用点约位于1 100 mm以内时，地基反力最大处均为近端端点处，这是端部效应的明显特征。

图3 地基反力的端部效应示意图Fig.3 Schematic diagram of end effect of reaction force

3.1.3 叠加效应

由前文分析可知，不同作用位置的预应力对钢带的作用符合叠加原理，钢带上任一点所受的地基反力等于各锚杆在该点处引起的地基反力的叠加总和。由图3可以看出，不同作用位置的预应力在钢带中部引起的地基反力数值适中且较为均匀，当端部效应不明显时，相互叠加之下钢带中部地基反力总值会高于钢带两端，此即叠加效应。

3.2 案例分析

根据叠加原理，锚杆预应力作用数目n值越大，则地基反力越大，支护效果越好，但是考虑到支护的经济性，锚杆数目往往受到限制。因此，在一定数目的锚杆作用下，通过控制变形协调系数β和锚杆预应力的作用位置x，使锚杆预应力经由钢带更均匀的传递到顶板，从而提高支护效果，是本计算的目的所在。

从支护材料特性来看，可以通过提高钢带的抗弯刚度来降低变形协调系数β值（式4），从而使锚杆预应力更均匀扩散；从支护设计来看，则需要考虑地基反力的端部效应以及叠加效应来合理布置锚杆的作用位置x。为了更直观的说明变形协调系数β、端部效应和叠加效应对顶板地基反力分布的影响，分别对3种锚杆布置方案的地基反力分布进行计算，并绘出不同特征参数条件下3种中心对称支护方案的地基反力分布曲线。

方案1：钢带全长l=4 200 mm，6根锚杆，排距800 mm，两端各留100 mm。

方案2：钢带全长l=4 200 mm，6根锚杆，排距700 mm，两端各留350 mm。

方案3：钢带全长l=4 200 mm，6根锚杆，排距600 mm，两端各留600 mm。

3种方案的地基反力分布曲线如图4。

图4 不同锚杆布置时顶板地基反力分布图Fig.4 Distribution of roof reaction force with different bolts arrangement

1）锚杆布置方式相同时，变形协调系数β值越小，地基反力分布越均匀。

2）当锚杆布置靠近钢带端部时（方案1），会受到较大的端部效应影响，地基反力分布曲线明显上凹，结合图3可知，仅位于100 mm处的锚杆在端点处引起的地基反力（1.32p）就超过了6根锚杆在钢带中点引起的地基反力总和（1.27p）。

3）当锚杆布置靠近钢带中部时（方案3），端部效应已不明显，此时叠加效应成为主导，在叠加影响之下中部地基反力偏大，曲线呈下凹状。

4）方案2中端部效应和叠加效应对钢带的影响近乎达到了平衡，顶板的地基反力分布曲线近乎平直，故3个方案中方案2最优。

综上，为提高支护效果，应使变形协调系数β越小越好。同时，锚杆布置时应同时考虑端部效应和叠加效应，均衡二者的关系，从而得到最优锚杆布置方案。

4 结语

1）建立了锚杆组合构件支护顶板的弹性地基梁模型，使用初参数法，求得了3根锚杆作用时地基梁的挠曲方程，经过演绎得出n根锚杆作用时钢带的挠曲方程，并进一步推得n根锚杆作用时顶板的地基反力分布方程。

2）变形协调系数β是影响锚杆预应力传递的重要参数，β值越小，则传递到顶板上的锚杆预应力越均匀。从围岩特性来看，岩层越软（地基系数kc越小），预应力传递越均匀，故预应力锚杆在软岩支护中更能发挥效力；从支护材料特性来看，可以通过提高钢带的抗弯刚度来降低变形协调系数β值，从而提高支护效果。

3）选择锚杆在钢带上的布置方式时应同时考虑地基反力分布的端部效应和叠加效应，端部效应影响下，钢带端部地基反力偏高，叠加效应影响下，钢带中部地基反力偏高，通过优化设计锚杆间距和边距，可以均衡端部效应和叠加效应，从而得到最佳锚杆布置方案。