考虑铰接间隙影响的液压支架四连杆机构运动误差分析

王帅

(平顶山天安煤业股份有限公司 五矿， 河南 平顶山 467000)

0 引言

液压支架是煤矿井下综采系统的重要机械设备，其主要作用是支护顶板和保障作业空间，因而液压支架的运动轨迹和运动精度受到越来越多的关注[1]。由掩护梁、底座和前后连杆组成的四连杆机构是液压支架的重要组成部分，该机构直接决定了支架顶梁前端的运动轨迹。理想的双纽线轨迹及其振动幅度是液压支架四连杆机构的设计基础[2-3]。然而，在生产过程中四连杆机构的尺寸误差和装配误差使运动副产生了铰接间隙，尤其在使用过程中摩擦磨损导致铰接间隙进一步增大[4]。铰接间隙使液压支架在使用过程中产生偏摆，支架顶梁前端实际运动轨迹偏离期望轨迹，导致液压支架稳定性下降，影响了支架的使用寿命[5]。鉴于液压支架四连杆机构铰接间隙对支架运动性能产生了负面影响，需要研究铰接间隙对支架运动误差的影响，为提高液压支架的设计质量和运动精度提供基础。

1 液压支架四连杆机构运动方程

以两柱掩护式液压支架为例，对其四连杆机构进行运动分析。两柱掩护式液压支架四连杆机构的运动简图如图1所示，其中ABCD为液压支架的四连杆机构，E点为掩护梁与顶梁的铰接点，CE杆为掩护梁，AB杆为前连杆，长度为L1，CD杆为后连杆，长度为L2。

图1 两柱掩护式液压支架四连杆机构

顶梁上下运动时，由铰接点E带动掩护梁CE杆运动，同时铰接点B驱使前连杆AB围绕机架铰接点A摆动，而铰接点C驱使后连杆CD围绕机架铰接点D摆动。这样四连杆ABCD就形成了一个封闭的运动矢量环，如图1所示，该四连杆机构的运动矢量方程可表示为

AB+BC=AD+DC

(1)

上式的复数表达式为L1eiβ+L3eiθ=L5eiγ+L2eiα，利用欧拉公式eiφ=cosφ+isinφ展开，并将实部和虚部分离，可得液压支架四连杆机构运动方程:

(2)

机架AD杆的水平倾角γ是固定值，如果前连杆AB的水平倾角β已知，则上述运动方程是关于α和θ的非线性超越方程组。该方程组难以通过三角函数关系直接求解，需要借助MATLAB工具编制牛顿—辛普森算法对非线性超越方程组进行数值求解。对于每个给定的β都对应两组解，通过程序控制，对求出的解进行判断和筛选。

获得各连杆的水平倾角后，掩护梁与顶梁的铰接点E的坐标可表示为:

(3)

2 含间隙四连杆机构位姿分析

液压支架四连杆机构中各连杆通过回转副连接，由于制造误差的影响，回转副的销轴和孔在机构运动过程中会出现间隙，而间隙将会使机构位姿产生变化。考虑间隙的回转副如图2所示，图2中的间隙进行了放大处理。假设回转副运动过程中销轴和孔始终保持接触，销轴不会悬浮于孔中，则孔中心与销轴中心形成偏心距。为了便于分析，将偏心距看作一无质量的连杆，其杆长为r，方位角为δ，δ∈[0, 2π]。由于销轴和孔的制造误差服从正态分布，因而随机变量r服从正态分布。

图2 考虑间隙的回转副

考虑回转副间隙影响的液压支架四连杆机构位姿如图3所示(间隙放大)，机构的理想位姿为ABCD，间隙影响后的位姿变为A1B1C1D1。各回转副的偏心距分别为ra、rb、rc、rd，对应的方位角分别为δa、δb、δc、δd。考虑间隙影响后连杆长度将会发生变化，如连杆A1B变为连杆A1B1，水平倾角由β变为β1。

图3 考虑间隙影响的液压支架四连杆机构位姿

3 平面连杆机构间隙模型

根据闭环矢量原理，回转副间隙影响的液压支架四连杆机构位姿矢量方程可表示为A1B1+B1C1=A1D1+D1C1。与式(1)相比，由于偏心距的影响，各杆件的有效杆长和方位角均发生了变化。有效杆长和方位角与连杆两端连接的运动副结构要素密切相关，如两孔型、孔销型和两销型杆件。以下将对这3种类型杆件的有效杆长和方位角进行具体分析。

1) 两孔型杆件。连杆的两端回转副要素均为孔，则该连杆为两孔型杆件。假设连杆机构中AB杆为两孔型杆件，如图4所示，AB杆的原杆长为L1，考虑间隙影响后变为A1B1杆，其有效杆长为LA1B1。通过图4可得闭环矢量方程AA1+A1B1=AB+BB1，采用欧拉公式将该方程表示为复数形式，并分离实部和虚部，可得:

图4 两孔型杆件

(4)

根据三角函数关系，将上述两式平方求和，忽略高阶分量后可得LA1B1与L1的关系为

L1+rbcosφb-racosφa

(5)

式中:φa为无质量杆AA1与AB杆形成的方位角，φa=β+δa；φb为无质量杆BB1与AB杆形成的方位角，φb=β+δb。

δa和δb两个随机变量在[0, 2π]内均匀分布，因而φa和φb也在[0, 2π]内均匀分布。ra和rb两个偏心距随机变量服从正态分布，其数值相对于杆长很小，故在进行分析时可取β1≈β。

2) 孔销型杆件。当连杆两端分别为孔和销轴时，该连杆为孔销型杆件，如图5所示的A1B杆。该杆件的原杆长为LA1B，考虑回转副间隙偏心距rb后，杆长变为LA1B1。由图5可知孔销型杆件的闭环矢量方程为A1B1=A1B+BB1。利用欧拉公式分离该矢量方程的实部和虚部，根据三角函数关系，将实部和虚部等式两边平方求和，忽略高阶微量后可获得孔销型杆件的有效杆长表达式:

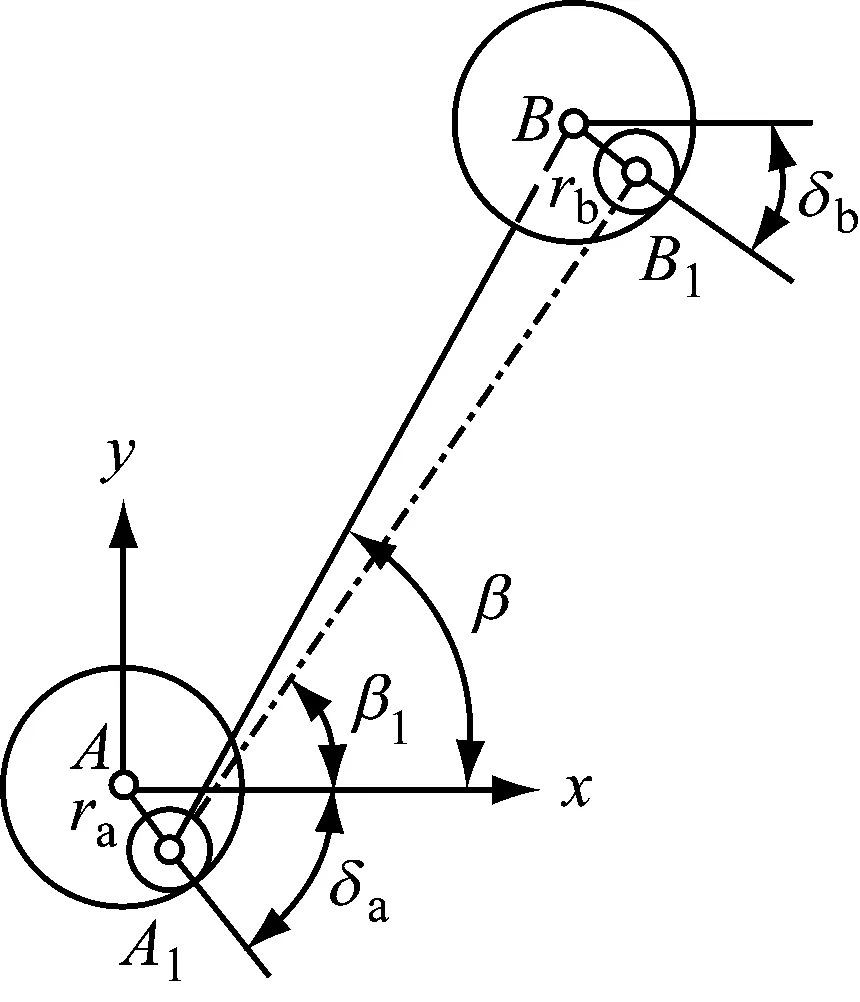
图5 孔销型杆件

LA1B1=LA1B+rbcosφb

(6)

由式(6)可知，孔销型杆件的有效杆长等于原杆长加上一个随机变量。

3) 两销型杆件。两销型杆件是指连杆的两端均为销轴，如图6所示的A1B1杆。由图6可知，该型杆件的原杆长LA1B1与有效杆长相等，因而回转副间隙对两销型杆件的有效杆长没有影响。

图6 两销型杆件

4 误差分析

以ZY4000/09/19型液压支架为例，计算考虑铰接间隙影响的四连杆结构运动误差。该机构各连杆的长度分别为：L1=730 mm，L2=940 mm，L3=340 mm，L4=1 030 mm。各回转副的偏心距服从正态分布，其均值为0.165 mm，标准差为0.031 8 mm。图1中AB杆和CD杆为两销型杆件，AD杆和BC杆为两孔型杆件，在进行误差分析时需要分别采用两销型和两孔型杆件间隙模型。

先不考虑各回转副间隙，利用式(1)和式(2)计算前连杆不同角度下绞接点E的理想坐标值。然后，将各连杆的杆长间隙模型继续代入式(1)和式(2)，计算考虑间隙影响下铰接点E的实际坐标值。不同前连杆角度下铰接点E实际坐标值与理想值的相对误差如图7所示。由图可知，横坐标误差大于纵坐标误差，最大误差小于2%，说明铰接间隙会使液压支架运动轨迹偏移，导致液压支架使用过程中不稳定因素增加。作为机架的AD杆对机构运动精度影响较小，AB杆和CD杆为两销型杆件，回转副间隙对这两个杆件的有效杆长没有影响。两孔型杆件CD杆不仅影响连杆的有效长度，还会导致方位角产生变化，因此连杆CD对液压支架四连杆机构的运动误差影响最大。后期需要结合国内外先进制造技术，不断提升液压支架连杆孔、底座孔、销轴的加工和装配工艺，减小销轴与孔的配合间隙。

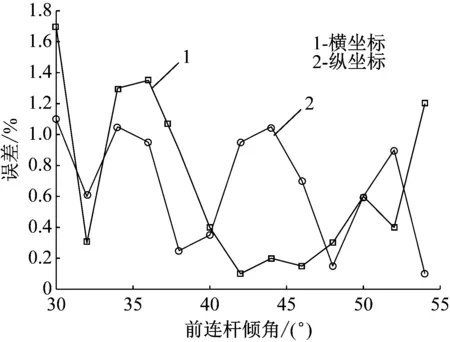
图7 铰接点E实际坐标值与理想值的相对误差

5 结论

基于闭环矢量原理推导了液压支架四连杆机构的运动方程，采用牛顿-辛普森方法对该方程进行求解。考虑连杆两端回转副元素，建立了两孔型、孔销型和两销型三种杆件的间隙模型。将相应的连杆间隙模型应用于液压支架四连杆机构运动方程进行运动误差仿真分析，分析结果表明最大运动误差低于2%，铰接间隙会使液压支架运动轨迹偏移，导致运行过程中不稳定因素增加。