预测算法在悬臂式掘进机悬臂控制中的应用

王 琨

（山西晋城无烟煤矿业集团有限责任公司成庄矿矸井运行队，山西 晋城 048021）

引言

掘进机被应用于破坏岩体和煤层，并将岩体和煤装载在车辆（卡车、复载机、输送机等）。适用于卧式、斜井掘进、竖井、施工等。随着掘进机的大量使用，有效地提高了煤矿的生产效率，也降低了劳动强度，保障了人员的安全。但是在掘进过程中悬臂的运动轨迹直接决定巷道的轮廓和方向。由于悬臂的运动轨迹精度差，导致载掘进过程中需要主控台不断地调整掘进方向和调整掘进机的姿态，降低工作效率，增加时间成本，浪费劳动力资源。本文提出一种应用于掘进机的悬臂控制控制算法，以保证其控制精度，提高采掘精度[1]。

1 反馈网络的搭建

如图1所示，悬臂上截割头的控制主要是通过四个伸缩油缸组成，其中两个负载控制截割头的左右摆动，另外两根负载截割头的上下摆动，从而可以实现截割头的运动要求。本文将截割头的垂直摆动和水平摆动单独分析。

图1 截割头的控制结构

截割头高度y与升降油缸的伸缩距离δ的关系为[2]：

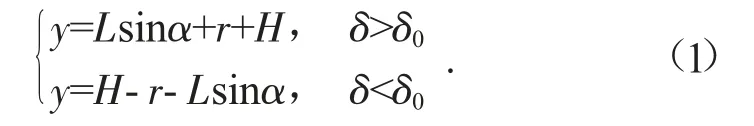
式中：L为悬臂长度；r为截割头半径；L为悬臂交接点与地面高度；α为绕中心的旋转角；δ0为截割头处于水平位置时升降油缸伸出距离，115 mm。δ0=115 mm。通过油缸参数和截割头的设计参数知道，截割头升降油缸行程距离0≤δ≤408 mm。

截割头左右摆动宽度x与回转油缸的伸缩距离w的关系为[2]：

式中：W为截割头外边缘与回转台轴线垂直距离；W1为截割头外边缘与回转台轴线水平距离；w0为截割头处于中间位置时回转油缸伸出距离，取238 mm；M为回转油缸伸缩的最大距离；为旋转角度。截割头回转油缸行程距离0≤w≤435 mm。

通过上面两个公式可以得出反馈量可以通过安装在伸缩油缸上的直线位移传感器实现，其型号为ks20，其分辨力为1 mm。

2 系统控制方案

如图2所示，数据采集是通过伸缩油缸上的直线位移传感器获取。其中掘进机完成固定动作并且整个过程实时数据采集，在通过预测控制输出，最后把输出量变为控制油缸伺服阀的电压量。其中采集到的位移信息就是预测控制的输入量，对输入量进行小波神经算法处理得到输出量。

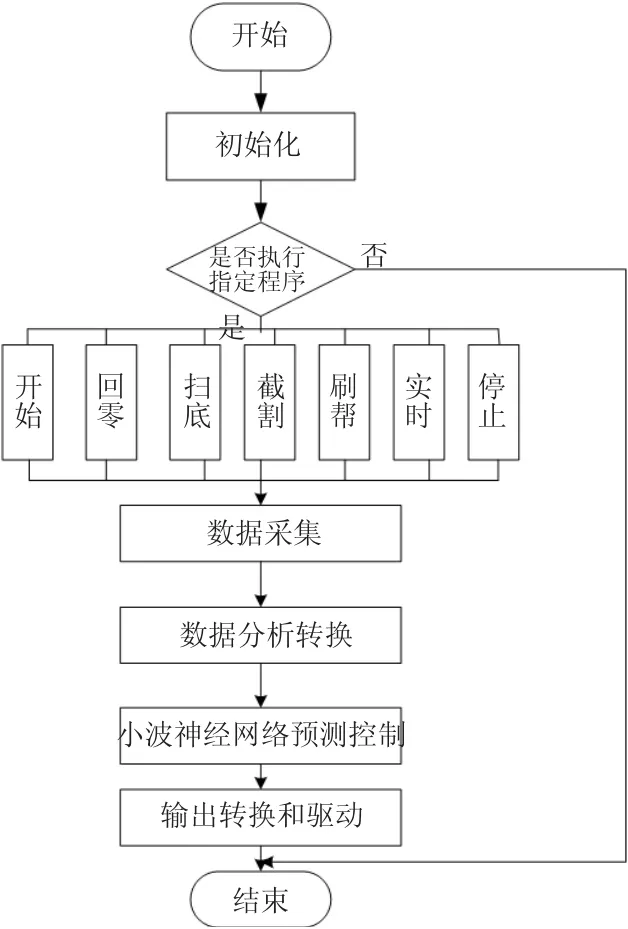
图2 系统流程图

如图3所示，采集到的数据要经过预测控制算法，该算法是通过labview中编写实现。其中每一个伸缩油缸的反馈数据都可作为算法的输入，最后得到修正的输出值，也是控制电液伺服阀的电压量。

图3 输出控制方式的实现

3 神经网络预测模型

建立该神经网络预测模型采用三层网络结构，其中一个是隐含层使用S型激发函数，输出层则使用线性激发函数。神经网络可以无限的接近非线性函数的曲线，该非线性系统可以用非线性离散时间模型表示为[3]：

式中：y（t）和u（t）分别为实时输入和输出值；m和n均为对象阶次；d为系统延时；f为非线性映射。

由于神经网络预测只需要对初始连接权进行调节，因此利用误差（E）反传算法对网络进行训练。其中训练方式是：已知各个节点数目，然后进行神经网络训练，利用二次型误差函数指标进行训练。由于多次调节仍无法满足精度要求，所以本次使用调整隐含层和反馈层节点数目：

神经网络预测控制器采用前馈信号完成，在该预测控制器中会选择几个未来控制量，把这几个控制量预测输出，使（2）式达到极小值。但是通常的预测控制算法，被控对象实的每一个控制量都要经过多个值来计算和优化。这样导致计算和控制规律的量很大。为了节约计算成本和时间。本文采用式（3）作为预测控制器的标准和网络控制器的学习二次型误差函数指标J：

式中：yr为给定输出；yp为预测输出；k为预测步长。

4 实验结果和结论

通过将神经网络算法输入到labview中，再将其采集信号的反馈量给到labview的输入，将输出给到控制器上。对掘进机悬臂的垂直运动和水平运动精度进行测算。

实际高度值是以地面为基准，未预测值是没有加神经网络预测算法的计算值，预测后值是加了神经网络预测算法的值，垂直摆动位置实验结果如表1所示：

表1 垂直摆动位置实验结果

实测数据把水平中心位置作为基准，未预测值是没有加神经网络预测算法的计算值，预测后值是加了神经网络预测算法的值，水平摆动位置实验结果如表2所示：

表2 水平摆动位置实验结果

从上表1、2得出神经网络预测算法可以提高掘进机截割头的运动精度，但是对水平控制精度的优化要弱于垂直控制精度的优化。