基于神经网络PID算法的四旋翼无人机优化控制

郭 婕，金 海，沈昕格

(浙江理工大学 信息学院,浙江 杭州 310018)

四旋翼无人机(Unmanned Aerial Vehicles，UAVs)是一种能够垂直起降具有对称结构的多旋翼飞行器。UAVs同一对角线上的一组旋翼顺时针旋转，另一组旋翼逆时针旋转，抵消了旋翼旋转带来的反扭矩力，保持了无人机平衡[1]。通过调节4个旋翼的转速，可以改变无人机的位置，实现对无人机飞行姿态的控制，例如悬停、俯仰、升降和横滚运动[2]。根据无人机布局和控制的不同，可将无人机分为“+”型和“×”型[3-4]。“×”型无人机姿态变换更加灵活稳定，且不会阻挡前方摄像头的视线，故本文采用“×”型结构无人机进行研究。

现有的无人机飞控算法主要有LQR控制、反步法控制、滑模控制等。文献[5～6]中设计了LQR(Linear Quadratic Regulator)控制器，并在仿真平台下进行了四旋翼飞行器的姿态跟踪和抗干扰实验。研究结果表明，LQR控制器对模型的依赖性较强，悬停时震荡，阶跃响应稳定态误差大。文献[7]发现反步控制法存在系统设计复杂的问题，会引起过参数化。滑模控制算法中含有不连续的切换项，容易造成控制输入的高频抖振[8]。传统的PID(Proportional Integration Differentiation)控制算法无需知道系统复杂的内部结构和参数，根据输入输出误差即可达到较好的控制效果。但是，PID的缺点是一旦参数整定完成就不可再修改，对于无人机这种控制要求较高的系统，无法实现较好的抗干扰控制。因此，本文结合神经网络的持续学习及权值修改的优点，设计了神经网络PID控制器，并与传统PID、串级PID做了对比，在建模仿真的基础上证明了其控制的有效性。

1 四旋翼无人机的数学建模

为了描述无人机的位置和姿态信息，首先需要建立坐标系。无人机的运动可以分解为六自由度的刚体运动，包含绕3个轴的转动和重心沿3个轴向的线运动。对于无人机的转动分析，要选用机体坐标系obxbybzb；对于无人机的线运动，要选用地理坐标系oexeyeze。从机体坐标系到地理坐标系之间的转换满足以下关系式[9-11]

(1)

式中，R为坐标转换矩阵

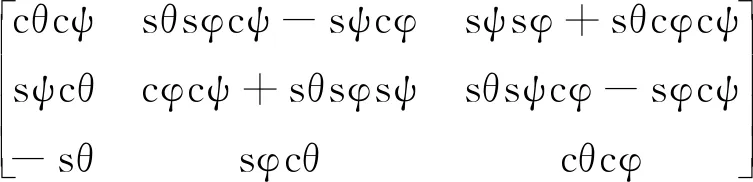
其中，s表示sin函数；c表示cos函数；θ表示无人机俯仰角；φ表示无人机横滚角；ψ表示无人机偏航角。

无人机的数学模型能够在仿真实验中评估控制算法的有效性。为了建立无人机的数学模型，这里做如下假设：四旋翼无人机是刚体；四旋翼无人机是严格对称结构，重心即几何中心；四旋翼无人机受的重力沿着大地坐标系z轴负方向，而螺旋桨拉力沿着机体坐标系z轴正方向。

以上这些假设简化了建模的过程，又能体现出无人机的运动特点。四旋翼无人机的建模主要分为3个部分：动力单元模型、刚体动力学模型、刚体运动学模型，具体如图1所示。

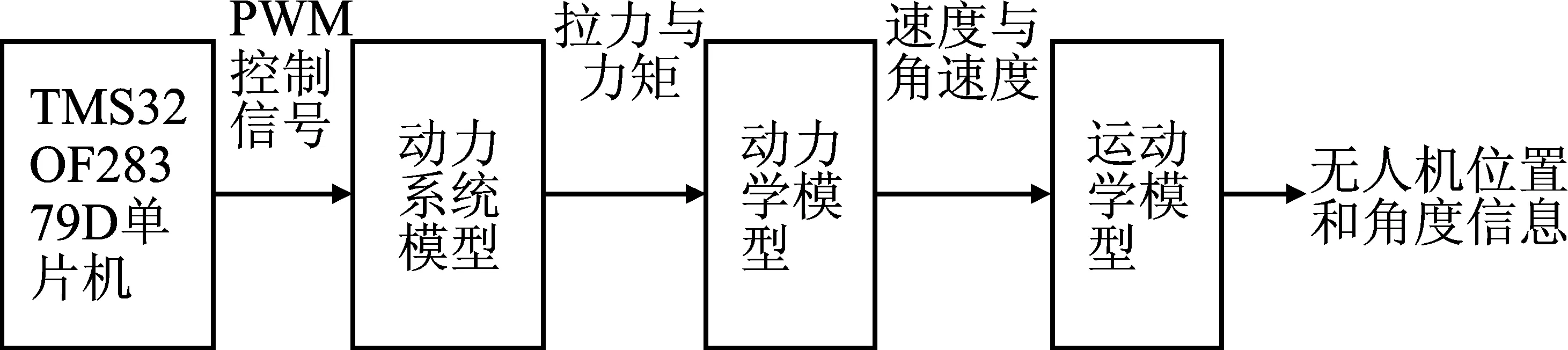
图1 四旋翼无人机模型

2.1 动力单元模型

无人机飞行控制是由主控芯片给出的PWM(Pulse Width Modulation)信号，该PWM信号通过电调转换成驱动电机的信号，通过电机带动螺旋桨的旋转带来升力。为了方便建模和调试，本文根据电机和螺旋桨参数建立了动力单元模型，该模型将PWM信号转换为无人机受到的拉力信息。配套电机与螺旋桨参数如表1所示。

表1 配套电机与螺旋桨参数表

根据对应的油门量和拉力数据在MATLAB中进行拟合，得到拟合曲线

y=1.515 4x+0.04523 2x2+6.253 9

(2)

根据该拟合曲线，在仿真模型中可以近似得到无人机的拉力信息，即输入油门量x的大小(也就是输出PWM占空比的大小)，进而得到螺旋桨带来的拉力

FT=y×g

(3)

式中，g是当地的重力加速度。

2.2 刚体动力学模型

分别从线运动和角运动两个方面分析无人机在空间中的运动。

2.2.1 线运动方程分析

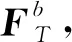
(4)

式中，m为无人机的质量；x、y、z分别为无人机沿着机体坐标系3个轴的位移。将上式分解到3个轴的线运动为

(5)

式中，FTi表示第i个螺旋桨提供的拉力；g为本地的重力加速度；Kx、Ky、Kz分别为沿着3个轴的空气阻力系数。

2.2.2 角运动方程分析

在合外力矩的作用下，机体绕轴做旋转运动，使无人机姿态角发生变化。无人机在飞行过程中受到的力矩作用主要有：4个旋翼提供的升力矩、空气力矩[13-14]。在机体坐标系中，根据欧拉方程，无人机的角运动微分方程可表示为

(6)

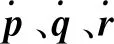
(7)

式中，L表示各旋翼到无人机中心的位置；c表示无人机力到力矩的转换系数；Ix、Iy、Iz分别为沿机体坐标系3个轴的转动惯量。

2.3 刚体动力学模型

运动学与质量和受力无关，因此，本文只研究位置、速度、姿态和角速度等变量。无人机的位置信息为[15-16]

(8)

无人机的角度信息如下式所示。

(9)

3 神经网络PID控制器

基于BP神经网络的PID控制系统结构如图2所示。控制器由两部分组成：(1)经典的PID控制器。PID系数由神经网络学习调整；(2)BP神经网络。根据输入输出误差，通过自身的学习能力调整网络的加权系数，不断调节PID的参数，使系统输出稳定。

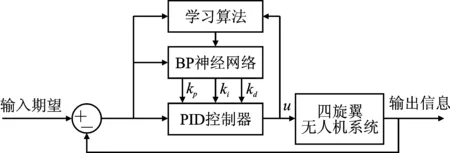
图2 神经网络PID结构图

经典增量式数字PID的控制算式[17-18]如式(10)所示。

u(k)=u(k-1)+kp(e(k)-e(k-1))+kie(k)+

kd(e(k)-2e(k-1)+e(k-2))

(10)

设BP神经网络NN采用3层BP结构，如图3所示，其包含3个输入节点，j个隐含节点，3个输出节点。输入变量的个数取决于被控系统的复杂程度。输出节点分别对应PID控制器的3个参数kp、ki和kd，输出层神经元活化函数取非负的Sigmoid函数。

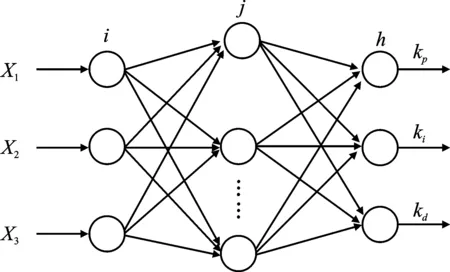
图3 神经网络结构图

隐含层的激励函数选取双曲正切函数，即

f(x)=(ex-e-x)/(ex+e-x)

(11)

输出层的激励函数选取非负的Sigmoid函数，即

g(x)=1/(ex+e-x)

(12)

取性能指标函数为

(13)

按照梯度下降法修正网络的加权系数，误差e(k)反向传播对每个权值w求导，可求得使e(k)减小的梯度。作为调整权值的方向，输出层权值的调整量和隐含层权值的调整量分别为

(14)

(15)

式中，η1、η2为学习率；α1、α2为惯性系数。权值更新之后正向传播计算出新的PID参数，再根据误差反向传播更新参数，循环直到满足条件。

4 无人机仿真系统整体设计

在 MATLAB-Simulink平台上搭建四旋翼无人机仿真系统整体模型，如图4所示，包括期望姿态输入、PID控制器、四旋翼无人机数学模型以及实际姿态输出4部分。首先设定期望的3个姿态角，通过PID控制系统以及无人机刚体模型，得到输出的实际姿态角信息，最后在示波器上显示。

为了得到更加接近实际的仿真效果，需要确定无人机数学模型的参数，如表2所示。转动惯量和机身阻力系数通过北航飞行测试系统[12]获得。

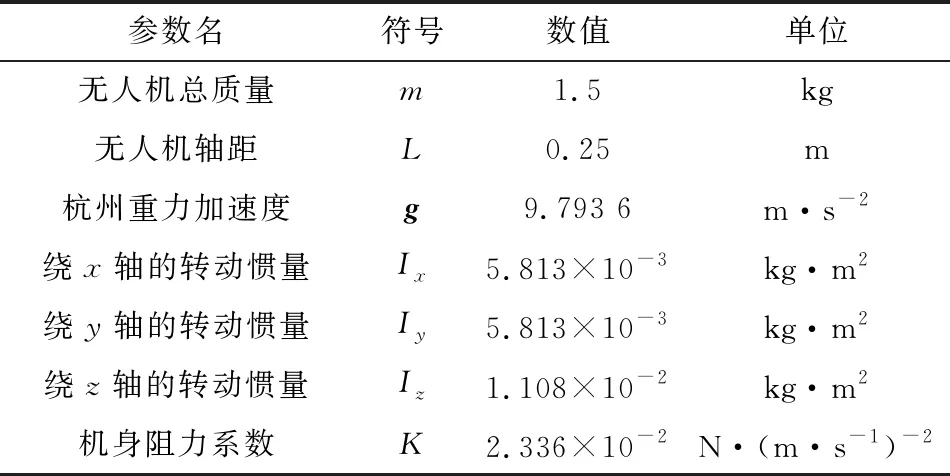
表2 无人机数学仿真模型参数

以Pitch角的调节为例，图5为神经网络PID根据输入输出误差自动整定PID参数的结果。该结果说明本文所提方法能够快速调整PID参数，得到较好的结果。

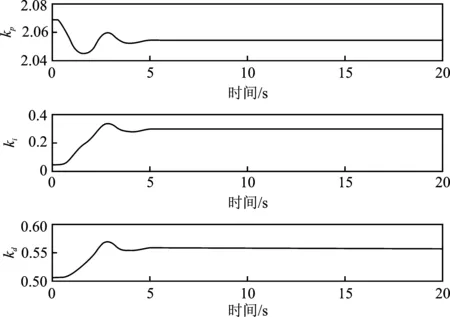
图5 神经网络PID参数整定结果

表3为经典PID、串级PID以及神经网络PID调节整定完成后的PID参数表。调整参数的过程中，经典PID和串级PID采用试凑法，耗时较长，且不一定会得到最优解。

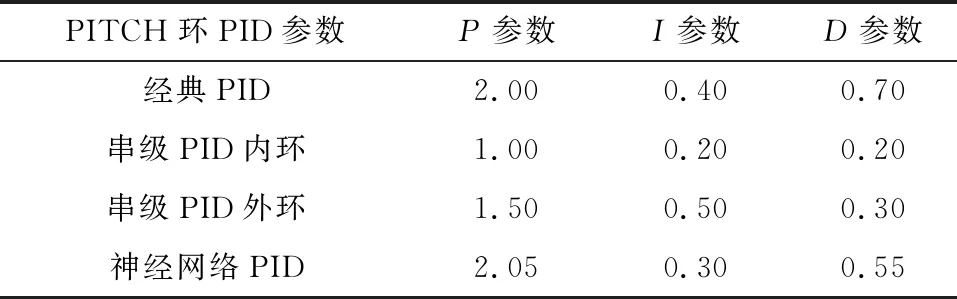
表3 无人机仿真PID参数

如图6所示，分别为Pitch期望角度与实际角度的曲线。可以看到，输出的实际角度基本与期望角度重合，在期望角度出现阶跃改变的时候，输出角度也能在很短的时间内同步变化。但是，经典PID调节刚开始有较大的超调和震荡，调节时间为4 s；串级PID较好地抑制了这种剧烈的震荡，但是调节时间仍然是4 s；神经网络PID不仅快速达到预期值，且在1 s内就将误差调节在了偏离静态值5%的范围内，没有出现明显的超调与震荡，动态性能更加优越。

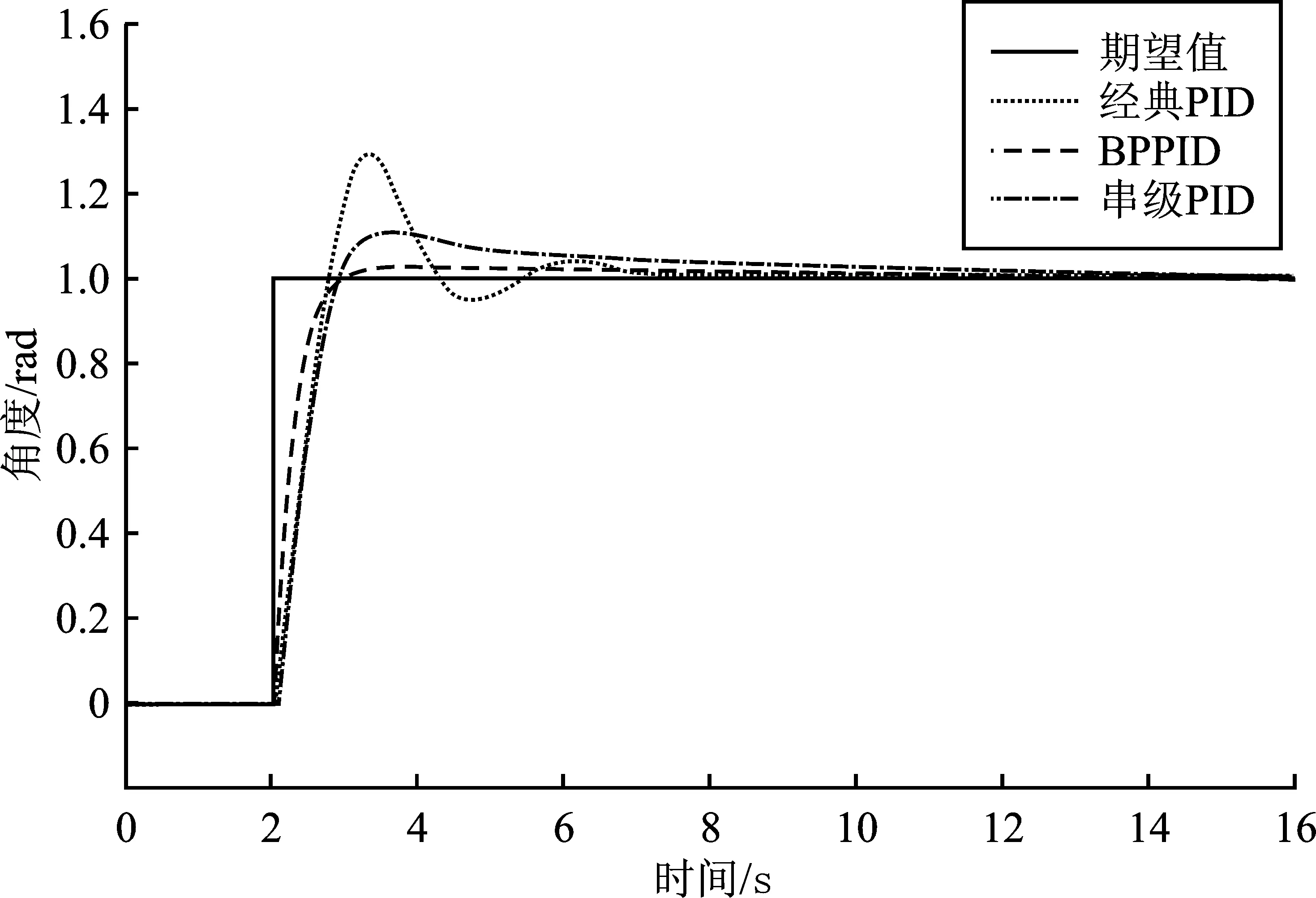
图6 不同PID控制方法角度跟踪曲线

如图7所示为3种PID控制器输出的误差曲线。后期输出较稳定时，经典PID仍有±0.005的震荡；串级PID有0.006的静态误差；神经网络PID有0.005的静态误差，可见神经网络PID控制效果最好，静态性能优于其他控制方法。

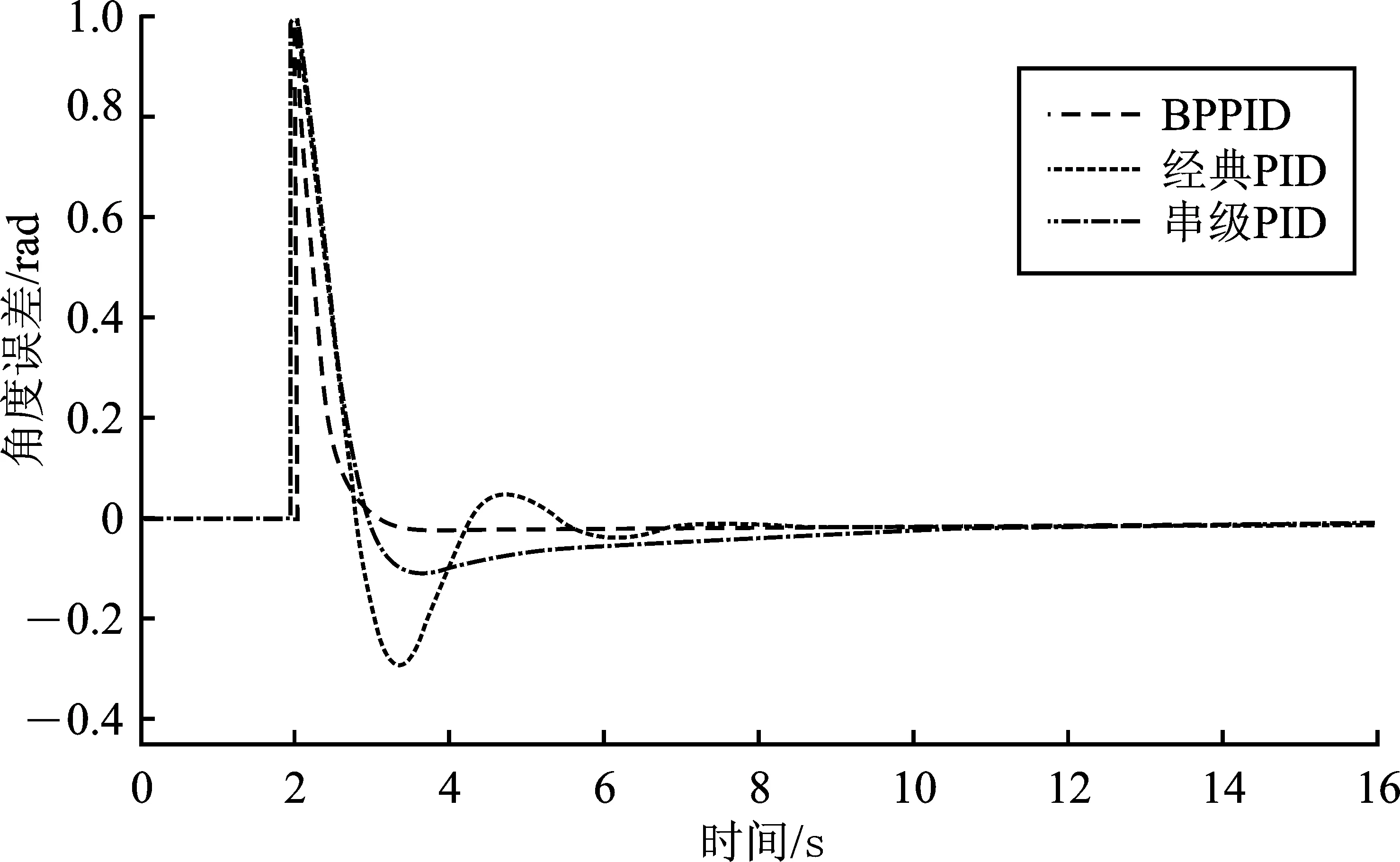
图7 不同PID控制方法的误差曲线

5 结束语

本文在阐述无人机飞行原理的基础上，建立了四旋翼、“×”字型结构无人机的仿真模型，在运动学建模和动力学建模中，考虑到了飞行空气阻力和空气力矩，并在此基础上进行了传统PID、串级PID、神经网络PID的控制。通过分析发现神经网络PID在非线性系统中具有良好的控制效果。本文仅研究了神经网络PID的姿态控制，今后将在此基础上进一步测试轨迹跟踪、自主飞行和自动避障。