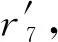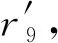虚拟纽结的区域不变量
2021-10-15胡冰清沈广艳
胡冰清,沈广艳
(东北师范大学数学与统计学院,吉林 长春 130024)
1 虚拟纽结的极小生成集
1999年,Kauffman[1]提出了虚拟纽结的理论.之前研究的经典纽结是把闭曲线嵌入到3维空间中,而虚拟纽结是把闭曲线嵌入到加厚曲面Sɡ×I(Sɡ为亏格是g的闭曲面,I为闭区间[0,1]).
两个虚拟链环图D和D′是合痕的,等价于D可以通过一系列的推广的R-移动,变成D′.
定义1[1]推广的R-移动:
(1) 关于经典交叉的经典的R-移动;
(2) 虚拟的VR-Ⅰ,VR-Ⅱ,VR-Ⅲ移动;
(3) “半虚拟”的semi-VR-Ⅲ移动.
定义2[2]一个虚拟链环是虚拟链环图模去推广的R-移动的一个等价类.
Polyak[3]讨论了经典纽结的定向的R-移动极小生成集.R-移动与VR-移动见图1.
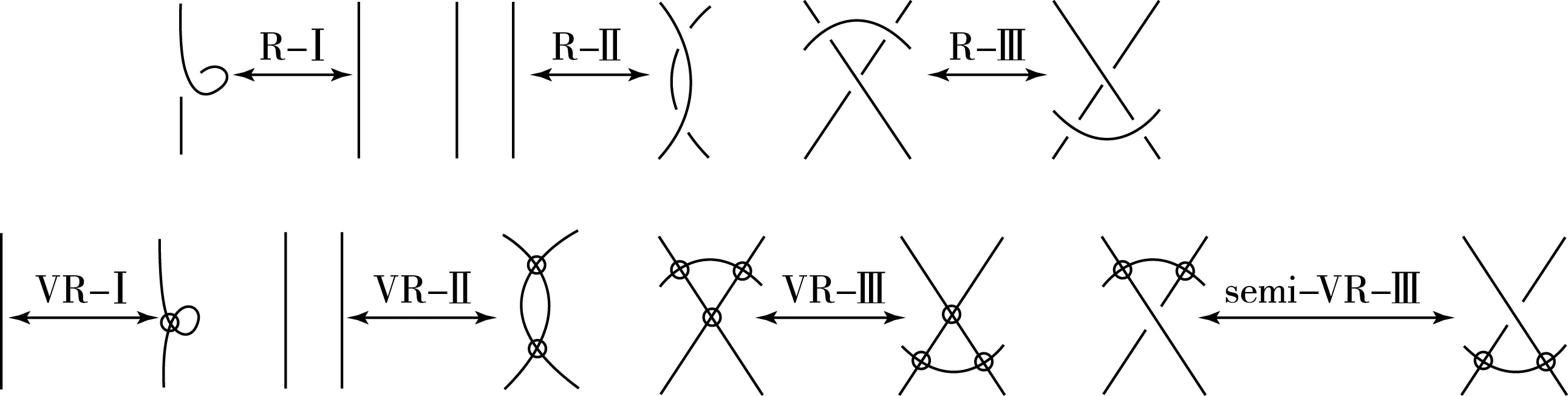
图1 R-移动与VR-移动
定理1[3]设D和D′是同一定向链环在R2中的两个投影图,则可以通过有限次4种定向的R-移动Ω1a,Ω1b,Ω2a,Ω3a,见图2,使D合痕于D′.

图2 定向R-移动
仿照文献[3],本文给出虚拟纽结的定向的推广R-移动的极小生成集.为此,先将所有的定向的VR-Ⅰ,VR-Ⅱ,VR-Ⅲ,semi-VR-Ⅲ的种类列出来.
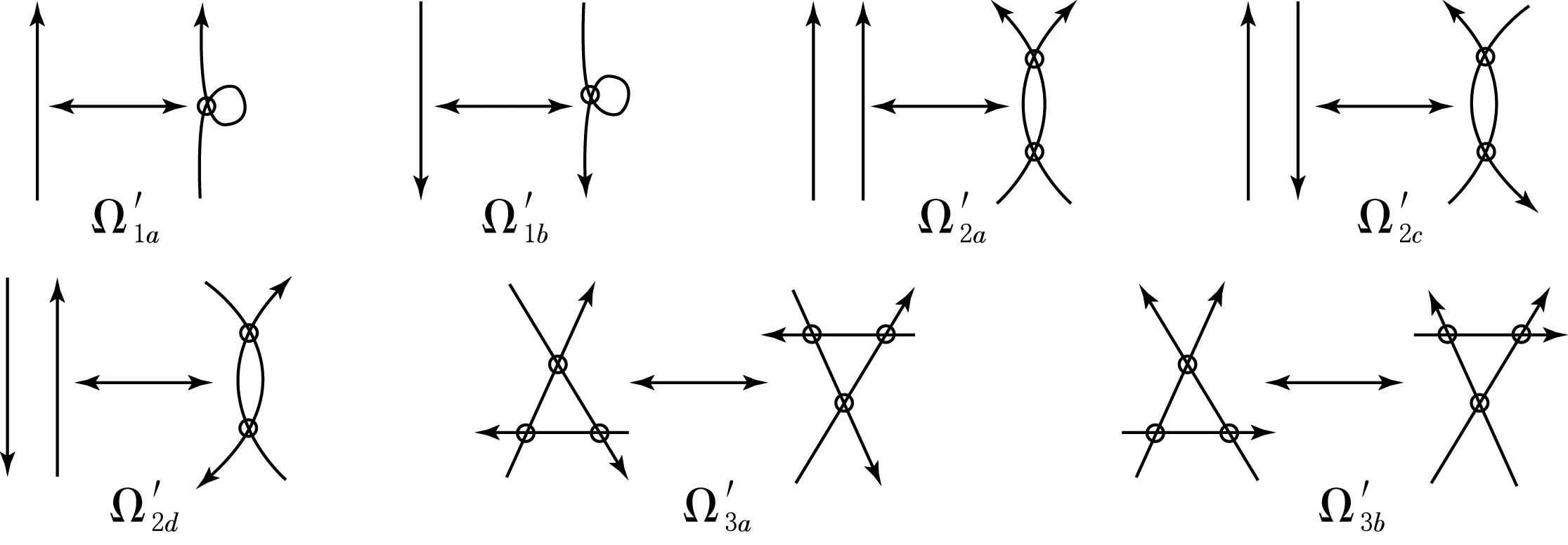
图3 定向VR-移动
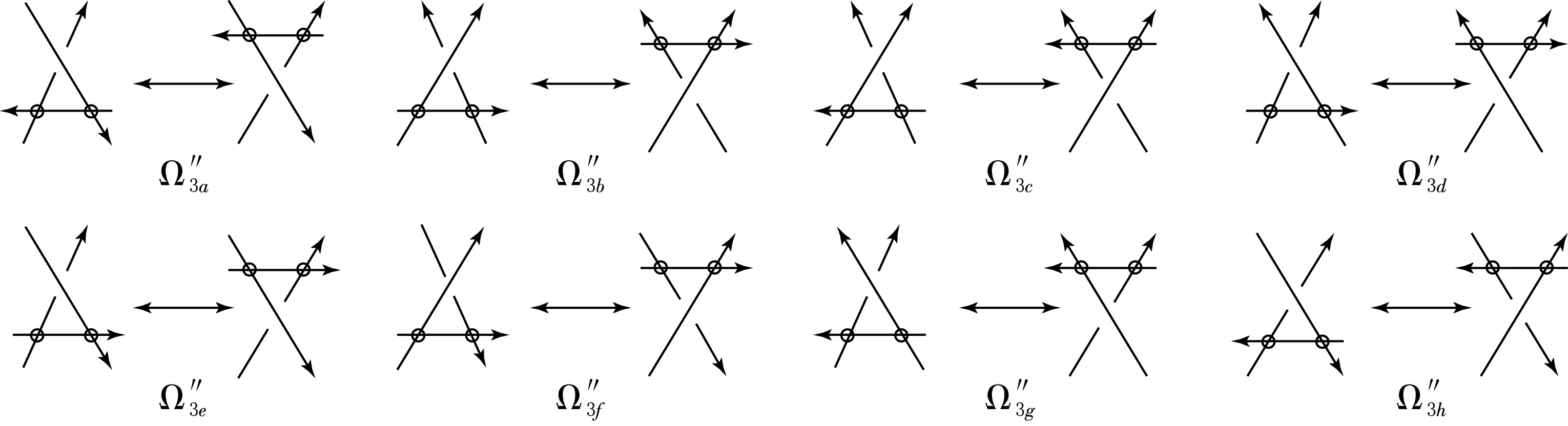
图4 定向semi-VR-Ⅲ移动

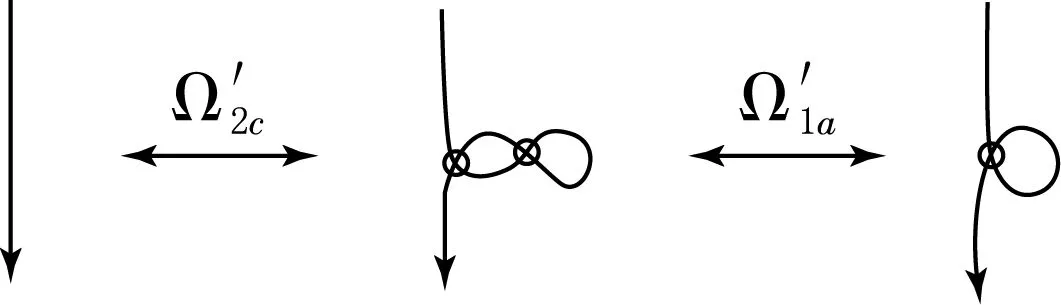
证明见图5.

图生成图
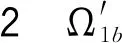
证明见图6.
图生成图

证明见图7.

图生成图

证明见图8.
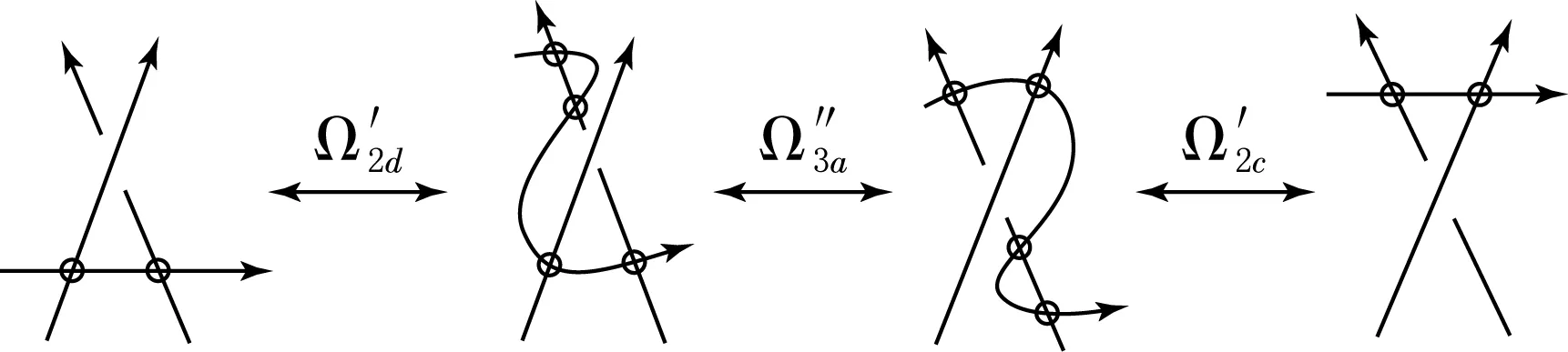
图生成图

证明见图9.
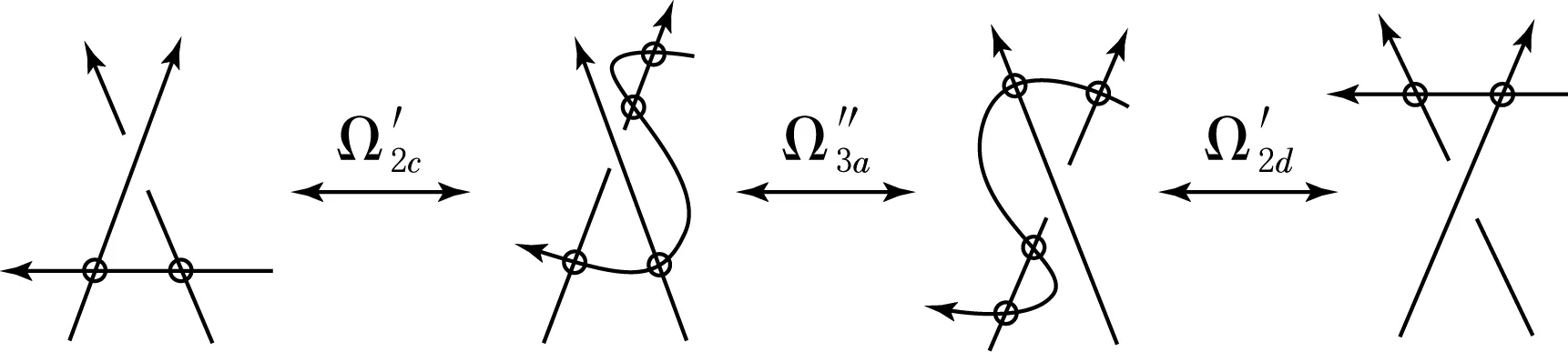
图生成图
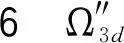
证明见图10.
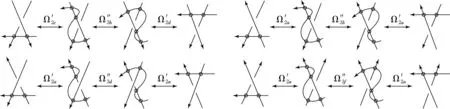
图生成图

证明由引理1—6可得结论.
2 虚拟纽结的区域不变量
Yang[4]构造了一个区域不变量,用一个纽结的平面图D把平面分成了很多个区域a,b,c,d,…,把每个区域都当成生成元,见图11,在每个交叉都增加一个线性关系ax+by+cz+dw=0.用LT(D)={a,b,c,d,…,r1,r2,r3,…}表示产生的代数结构.称之为D的一个线性的tridle.[5-7]R-移动的不变性表明条件xz=yw一定要满足.
对虚拟纽结投影图中的经典的交叉仍定义关系r:ax+by+cz+dw=0,其中xz=yw.对虚拟交叉定义关系r′:ax′+by′+cz′+dw′=0.要求x,y,z,w,x′,y′,z′,w′可逆.下面,记LT(D)={a,b,c,d,…,r1,r2,r3,…},给出LT(D)为虚拟纽结不变量时,应满足的代数结构.
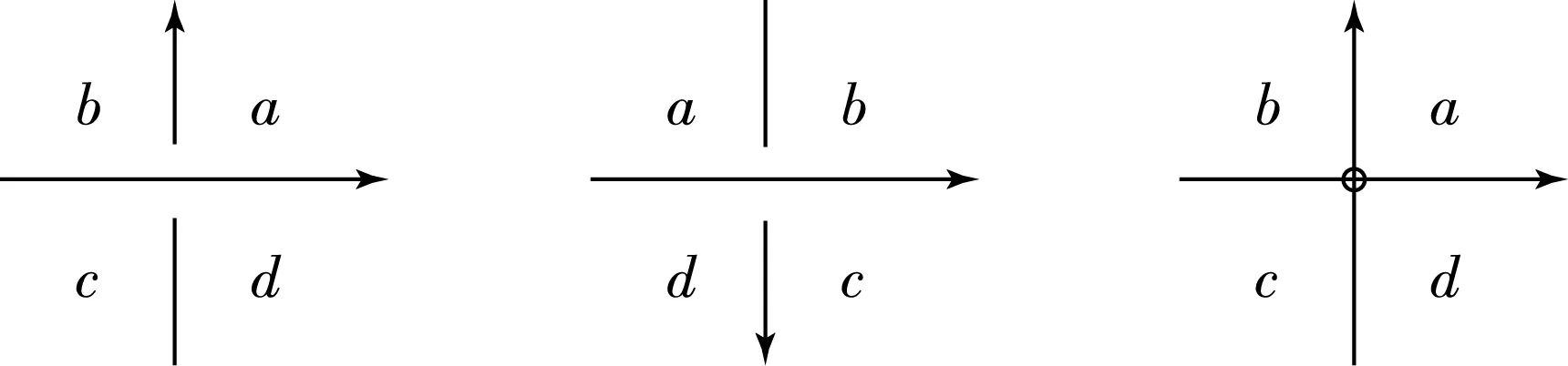
图11 定向虚拟纽结区域生成元
定理3LT(D)是一个虚拟纽结的不变量.
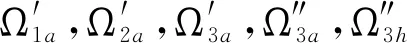
首先对虚拟的VR-Ⅰ,如图12所示,将每个区域分配生成元a,b,c,….LT(D)={a,b|r1,r2,…}.那么在D′中,生成元满足bx′+ay′+bz′+cw′=0,LT(D′)={a,b,c,…|bx′+ay′+bz′+cw′=0,r1,r2,…}.应用文献[4]的Tietz变换消去c和c的关系,得LT(D)≅LT(D′).
对虚拟的VR-Ⅱ,如图13所示,将每个区域分配生成元a,b,c,….LT(D)={a,b,c|r1,r2,…}.那么在D′中,生成元满足bx′+ay′+dz′+cw′=0,dx′+ay′+bz′+cw′=0.故有x′=z′.那么在D′中,LT(D′)={d,a,b,c,…|bx′+ay′+dz′+cw′=0,r1,r2,…}.应用文献[4]的Tietz变换消去d和d的关系,得LT(D)≅LT(D′).
对虚拟的VR-Ⅲ,如图14所示,将每个区域分配生成元X,Y,E,….LT(D)={X,Y,E,F,T,U,V,…|r1,r2,…}.
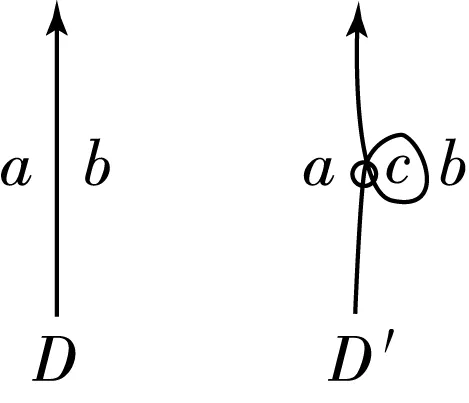
图12 定向VR-Ⅰ区域生成元
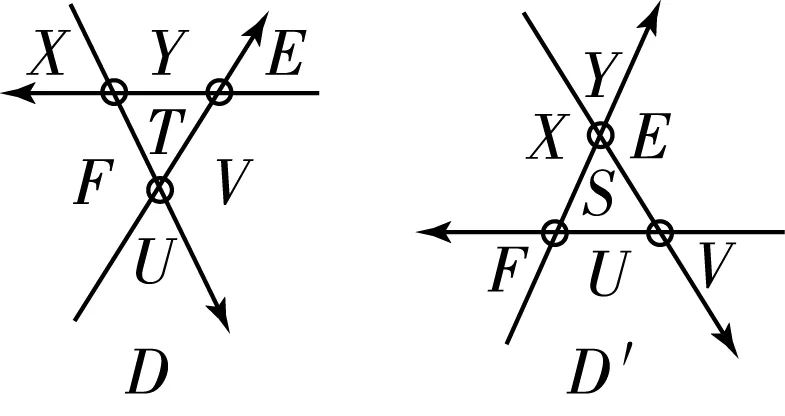
图14 定向VR-Ⅲ区域生成元
r4:Fx′+Ty′+Yz′+Xw′=0;
r5:Yx′+Ty′+Vz′+Ew′=0;
r6:Vx+Ty+Fz+Uw=0.
把T,U,V当成未知的,由r4,有T=-{Fx′+Yz′+Xw′}/y′.把T的表达式代入r5中,有V={Fx′+Xw′-Ew′}/z′.把T,V代入r6中,有
在D′中,这里有3个交叉,所以有3个关系式:

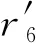
所以
在K中,有3个交叉.所以有3个关系式:
r7:Fx+Ty+Vz+Uw=0;
r8:Fx′+Ty′+Yz′+Xw′=0;
r9:Yx′+Ty′+Vz′+Ew′=0.
由r8,有T=-{Fx′+Yz′+Xw′}/y′.代入r9,有V={Fx′+Xw′-Ew′}/z′.将T,V代入r7,有
在K′中,有3个交叉.所以有3个关系式: