装备模拟训练系统数据离散化
2021-10-15付朝博
邓 青, 薛 青, 杜 楠, 付朝博
(1.陆军装甲兵学院演训中心, 北京 100072; 2.68303部队, 格尔木 816099)
装备模拟训练系统数据预处理主要是用于挖掘前对数据展开治理,包含必要的数据融合、数据清洗、数据离散化、数据变换等步骤,从而使数据符合挖掘方法和挖掘模型的输入标准[1]。数据离散化是其中的一项重要工作,在装备模拟训练系统的实际使用中,按照不同的应用场景以时间、空间顺序采集了大量数据,涉及地理位置、机动路线、毁伤概率等连续型数据[2]。这些数据表达过于细化,不利于数据挖掘发现简洁的模式和知识,另外对噪声也非常敏感,一旦出现细小的误差可能会造成两个数据的比较值不相等。而数据离散化是在最小化信息损失的前提下,根据设定的离散化准则选择连续型数据的若干个最优划分,将连续型数据转化成少量的有限区间,同时采用整型或字符型数据量化离散化区间的值。因此,通过对装备模拟训练系统数据进行离散化处理,能够有效简化数据,满足挖掘算法的适用需求,提高挖掘算法的学习能力,从而提取有价值的规则。
数据离散化方法主要分为无监督和有监督两类。无监督离散化不使用类标签,通过数据的分布特征对单个属性进行划分,实现方式简单,但最终离散的精度难以保证,尤其当数据分布极度不平衡时会产生较差的结果。等宽算法[3](equal width, Equal-W)是应用广泛的无监督离散化算法,根据预先设定的参数,将连续数据划分为若干个等宽区间,由于未考虑数据分布特点,算法易受噪声影响。文献[4]运用频率模式增长(frequent pattern growth, FP-Growth)算法挖掘火炮模拟训练系统数据,采用连续型数据结构,存储代价大且随着数据增长搜索效率下降。文献[5]对坦克驾驶模拟训练操作数据首先进行规范化、离散化等预处理,然后采用支持向量机进行分类挖掘,实验证明在数据离散化处理后,能更好地提取泛化知识。文献[6]基于定制的专门离散化算法研究了坦克驾驶模拟训练数据,用于辅助装备使用决策,同时能减少昂贵的装备测试费用。文献[7]提出Chimerge离散化算法将连续型数据的每个不同取值作为一个单独的区间,采用χ2统计量对相邻区间测试,并优先合并χ2最小的区间,直到所有区间的χ2都小于指定的阈值。文献[8]提出自上而下的MDLP(minimum description length principle)离散化算法,选择信息熵最小的点作为分割点,递归操作直到满足最小描述长度准则。
从上述的数据离散化方法可以得出,多数是采用单属性离散化,即在每次离散化的过程中,只考虑一个属性,然后按照设定的离散化准则循环迭代,直至每个属性处理完毕[9-11]。这些方法具有简单易理解、执行速度快的特点,但往往忽视了属性之间的相关性、互补性,割裂了属性之间的联系。而对于装备模拟训练系统实际运行产生的数据,往往几个数据属性之间是相互作用、共同影响的[12-13],比如,在运用坦克驾驶模拟训练系统进行驾驶操作技能训练时,对油门、离合器、制动器的操作并不是孤立的,应该相互配合才能更好掌握操作要领,提高训练成绩,因此,在对油门、离合器、制动器的操作数据进行离散化时,必须要考虑它们之间的相互作用,否则在后续进行数据挖掘时会产生错误的知识。针对装备模拟训练系统数据离散化存在的问题,提出一种基于层次聚类和相容度的数据离散化方法(discretization algorithm by hierarchical cluster and compatibility,DHCC)。该方法属于有监督、自下而上的处理过程,首先通过动态确定簇数对数据的所有属性进行层次聚类,实现对各属性的初始整体划分,然后运用相容度差值指导相邻区间的合并,有效去除冗余区间,从而获得全局最优属性区间集合。实验阶段对DHCC离散化算法进行了比较,并在实际数据集上进行了验证。
1 装备模拟训练系统数据离散化过程建模
根据装备模拟训练系统产生的数据特点,通常包含条件属性和类别属性,一组条件属性通过相互作用共同决定了类别属性。因此,采用决策表将这些属性表示成数据集合的形式,从而便于直观地对装备模拟训练系统数据离散化过程进行建模分析。首先给出装备模拟训练系统数据决策表有关定义。
定义1从装备模拟训练系统关系数据库中抽取数据挖掘所需要的数据集B,将其转化为四元组的数学表达形式S=〈U,A=C∪D,V,F〉,其中,U为数据对象集,A为属性集,包含条件属性集C和决策属性集D,V为值域集,F表示数据属性到值域的映射,则称S为决策表。
对装备模拟训练数据离散化需要结合实际的挖掘任务,将连续属性转变成离散属性、定量数据变换为定性数据。根据以上分析,对装备模拟训练系统数据离散化过程模型描述如下。
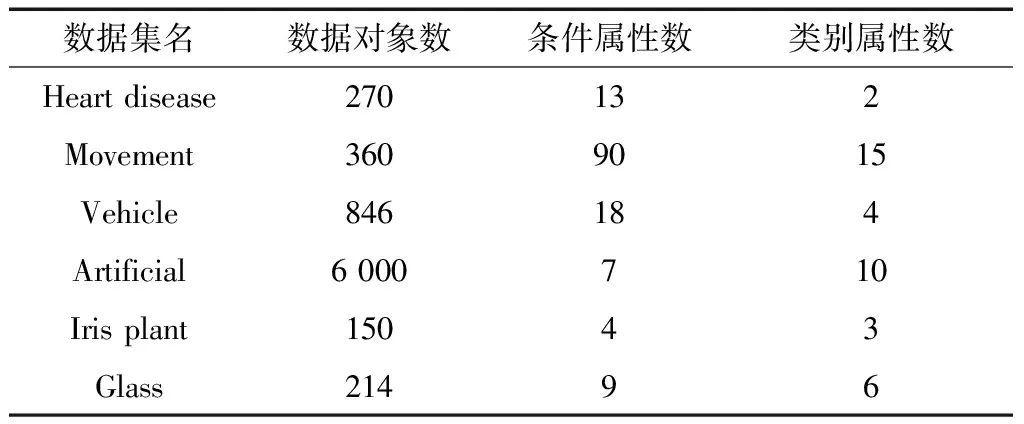
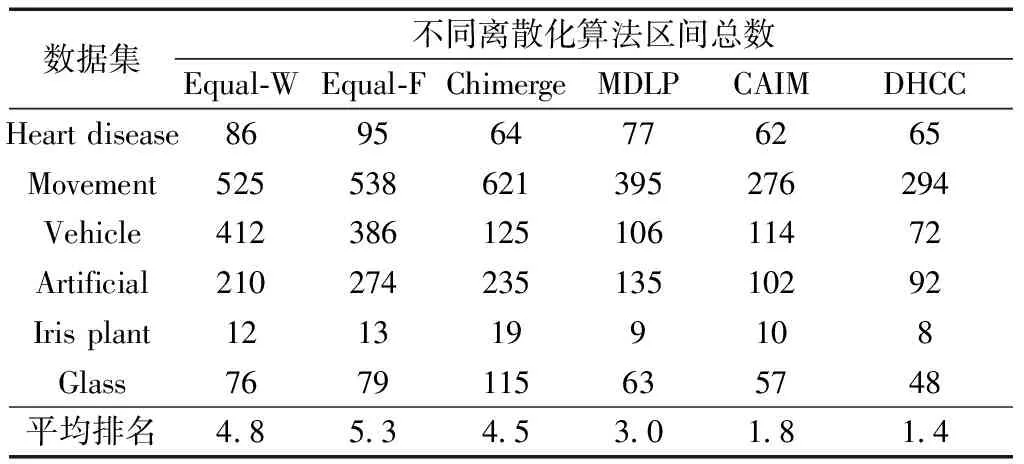
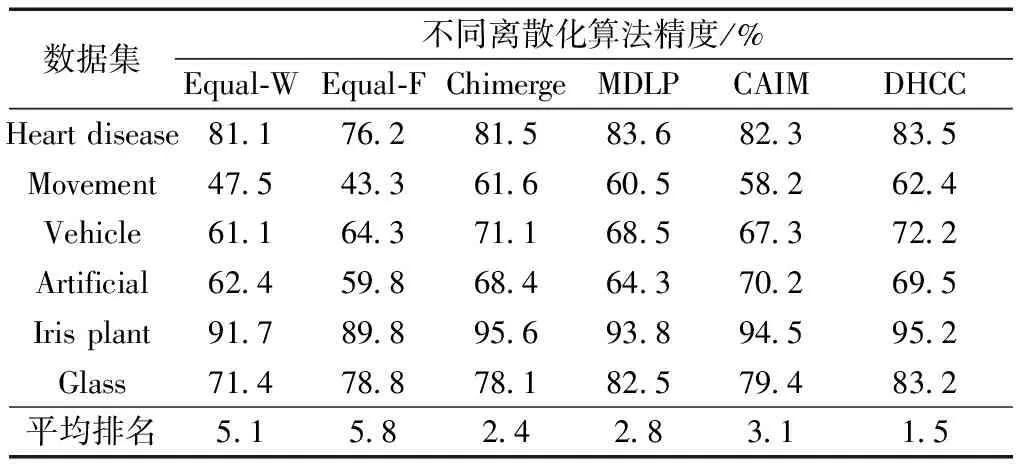
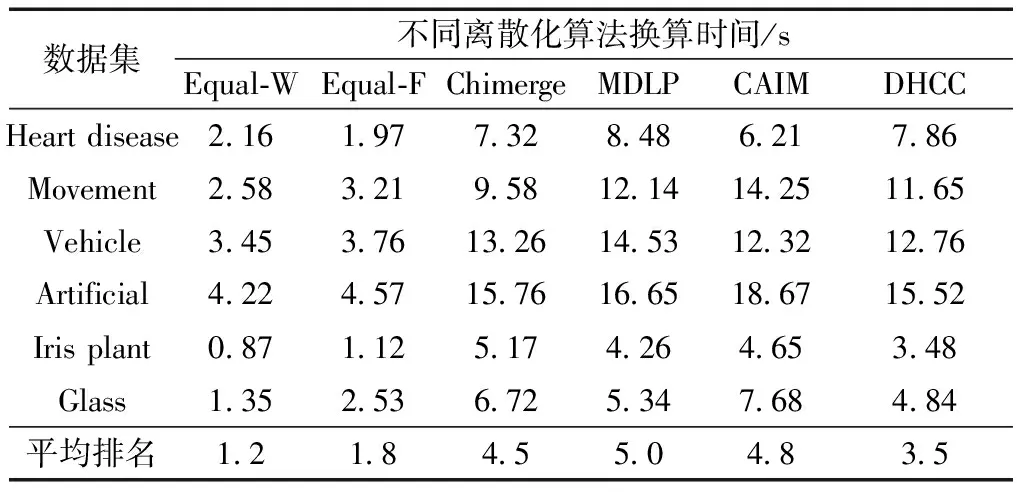
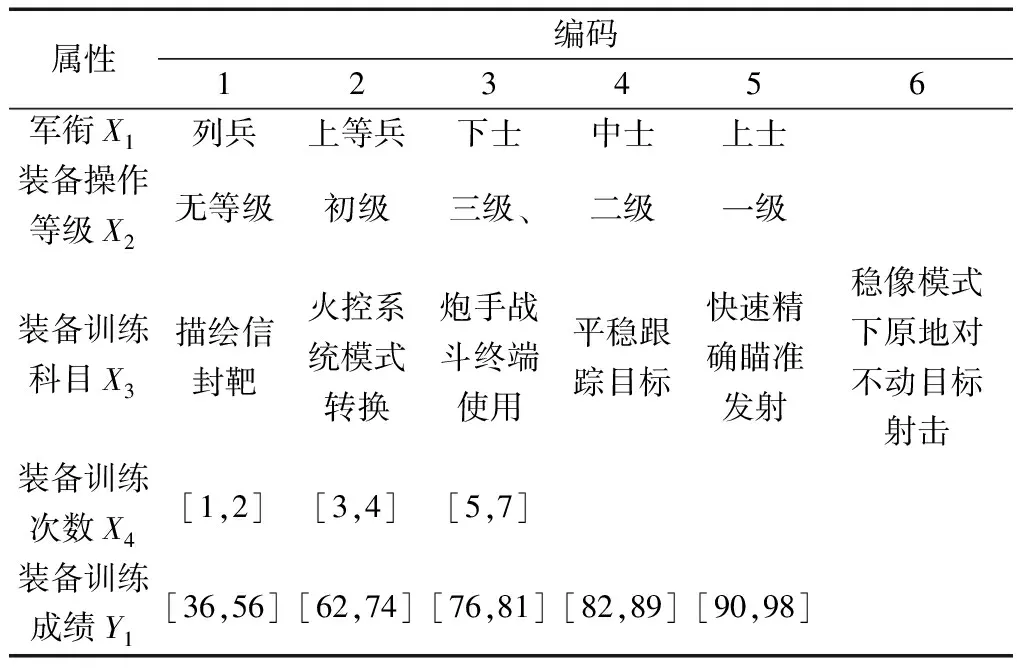
假设装备模拟训练系统数据采用决策表S=〈U,A=C∪D,V,F〉表示,数据对象u∈U,属性c∈C,c的值域为Vc=[lc,hc],则存在F(u,c)∈Vc。设值域Vc上存在一分割点集合T={(c,a0), (c,a1),…, (c,an)}则T将Vc划分形成区间集合Pc={[a0,a1), [a1,a2),…, [an-1,an]},其中lc=a0 ∃c(u)∈[ai-1,ai),i∈{ 1, 2, …,n},根据属性到值域的映射FP(u,c)可计算连续属性c的所属区间i,因此通过P={Pc|c∈C}将原决策表S=〈U,A=C∪D,V,F〉转化成离散型决策表SP=〈U,A=C∪D,VP,FP〉。与原决策表相比,离散化后的决策表SP改变了属性A的值域,对原有的取值范围采用了有限个区间进行划分,并用离散的数值标记每个区间,区间范围内的数据都会被离散值所取代。 对于装备模拟训练数据决策表既包含连续型,又含有离散型数据,属于混合型决策表,比如运用步战车模拟训练系统产生的数据既有电路总开关、音响按钮等状态数据,还包括油门装置、发动机转速等连续数据,有时不仅需要对连续型数据离散,为了挖掘出更加简洁的作战规则,在必要的时候对离散型数据也需更进一步的泛化处理,由此建立装备模拟训练系统数据离散化总体框架如图1所示。其关键在于研究提出适当的数据离散化算法,同时满足混合型决策表离散化的需求。 图1 装备模拟训练系统数据离散化的总体框架Fig.1 Framework of equipment simulation training system data discretization 基于层次聚类和相容度的装备训练系统数据离散化方法,首先通过层次聚类,并结合属性间的关联,计算簇的正域调整确定聚类数目,实现对属性的初始划分。然后结合类别属性信息,运用简化的相容度对初始离散化结果的相邻区间进行合并,减少断点数和去除冗余区间,从而生成最终的离散化方案。 层次聚类是对整个决策表的所有条件属性同时进行,可以更好地保持属性间的关联(和分类精度下降问题)。在聚类前,为便于比较数据对象间的相似性,对∀c∈C的属性值进行标准化处理,处理依据为 (1) 式(1)中:max[c(U)]、min[c(U)]分别表示整个决策表中属性c的最大值和最小值。初始时将整个U中的每个对象都看作一个簇,选择欧氏距离建立簇之间的相似度矩阵(simulation matrix, SIM),矩阵元素SIMij表示ui和uj之间的距离,即 (2) 选择矩阵SIM中最小元素所对应的两个数据对象进行聚类,对新形成的簇与其他数据对象的相似性按照平均距离计算,尔后更新相似度矩阵,删除原来的两个数据对象。依此循环迭代进行聚类,直到满足事先指定的聚类个数,但装备模拟训练系统数据所形成的决策表无法预知簇的个数。针对这一问题,利用数据自身的固有特征,在每次聚类过程中,计算正域的变化,当值减少表明聚类后出现了不一致性的数据,对该簇的聚类过程应当终止。反之表明聚类后没有降低正域,可以继续进行聚类,依次迭代直到处理完所有的数据对象。 假定最终生成的聚类数为L,将形成的每个簇向条件属性空间进行投影,可得到每个属性的一系列取值区间。以属性c为例,对于第k个(1≤k≤L)簇所包含的数据对象集合为Uk,则属性c在该簇中的取值集合为 (3) 进一步可得出属性c在该簇的区间为 (4) 则属性c在各个簇的左、右区间集合表示为 (5) (6) 对上述两个区间集合的元素按从小到大进行排序,得到属性c的初始划分区间为 (7) 第一步的层次聚类用于初始划分属于无监督离散化,运算效率高,但容易导致相似的区间被分离,且随着属性数量的增多,产生的区间也会增加,因此,通过引入类别属性信息,同时结合相容度指导区间合并,以此最小化属性的区间数,提高离散化效果。 区间合并前,首先需要确定合并的优先级。根据信息论,熵值反映了数据的类分布特征。进一步,如果属性区间的信息熵越小,则相应的类分布一致性越高,属性区间的重要程度就越低,特别是当区间的信息熵为0时,相应的类属性完全一致,该区间的重要程度最低,不会对其他属性造成影响,应作为区间合并的首要选择。因此,重要程度低的属性区间优先合并。 (8) (9) (10) 为了体现不同属性区间相对于类属性的联系,将所有属性区间的信息熵进行排序,选择信息熵最小的相邻区间作为候选合并对象,确保每个属性区间均有被选取的机会。 在执行合并的过程中,需要保持整个决策表的一致性不变,以此作为区间合并的判断条件。为实现这一目的,通过采用计算合并后的相容度φ′,并将其与原始的相容度φ0进行比较,可以避免传统采用人工设定阈值作为合并判断条件带来的误差。即 Δ=φ′-φ0 (11) 当Δ<0,表明相容度减少,合并后引起了决策表的不一致性,对这个区间的合并应当终止,并将这一相邻区间标记为不可合并状态,后续也不会成为候选的合并对象。反之当Δ≥0,表明合并后决策表的一致性仍然满足数据集的精度要求,可以执行区间合并。依次选择需要合并的下一个相邻区间,直到所有相邻区间处理完毕或剩下的相邻区间已被标记为不可合并状态,从而得到最终的离散化区间集合。 求解合并前后决策表的相容度是一个计算密集型过程,尤其是迭代操作将会耗费大量时间。针对这一问题,在计算过程中进行了简化,即当每次相邻区间合并,决策表相容度的变化主要是由相邻区间合并所引起的,对于未参与合并的其他区间对相容度的变化不会带来影响,这些属性区间的一致性不变。因此,在计算相容度变化时只考虑待合并的相邻区间,具体推导为 Δ=φ′-φ0= (12) 式(12)中:POS表示粗糙集中的正域关系;IND表示等价关系。 根据前两节的分析,基于层次聚类和相容度的数据离散化算法具体流程如图2所示。 图2 算法流程图Fig.2 Algorithm flow chart 输入:原始决策表S=〈U,A=C∪D,V,F〉,C={c1,c2,…,ck}为所有条件属性的集合,即待离散化的属性。 输出:最终的离散化决策表。 Step 1标准化处理,为比较数据对象间的相似性,对∀c∈C的属性值按式(1)进行处理。 Step 2 Step 2.1:将整个U中的每个数据对象视为一个单独的簇,构建初始相似度矩阵SIM。 Step 2.2:选择SIM中最小值所对应的两个元素作为聚类的候选对象,按式(2)计算新形成的簇的正域。 Step 2.3:根据正域的变化情况,若出现了不一致性的数据,则放弃该簇的聚类,转到步骤Step 2.2。否则转到Step 2.4。 Step 2.4:对候选的数据对象执行聚类,并更新聚类后的相似度矩阵。 Step 2.5:判断U中的数据对象是否处理完毕,若没有则转到Step 2.2。否则转到Step 2.6。 Step 2.6:由式(7)计算得到每个属性的初始划分区间。 Step 3 Step 3.2:优先合并信息熵为0的相邻区间,然后选择重要程度最低的区间进行合并。 Step 3.3:计算合并后相容度的变化Δ=φ′-φ0,当Δ≥0,转到Step 3.4。否则终止区间的合并,转到Step 3.2。 Step 3.4:判断是否还有相邻区间需要处理,若没有则转到Step 4。否则转到Step 3.2。 Step 4对最终形成的区间用整数或字符进行编码,完成最终的离散化。 对基于层次聚类和相容度的数据离散化算法的四点说明: (1)Step 2.3结合正域的计算判断数据的一致性,考虑了条件属性与类别属性之间的关联,使聚类更加合理。 (2)Step 3.2计算区间信息熵并按从小到大进行排序,以此度量区间的重要程度,这一步骤是对条件属性集合同时进行比较,确保每个属性得到一致处理,避免了对单个属性过度离散化。 (3)为提高算法效率,Step 3.3采用了简化的相容度差值计算。 (4)当区间的信息熵为0时,相应的类属性完全一致,合并后不会影响数据的一致性。当出现多个区间信息熵一致的情形时,优先选择类属性一致性较高的区间。 为验证DHCC离散化方法的性能,选择UCI机器学习数据库中6个标准数据集进行实验(装备模拟训练系统数据属于涉密范围),分别为Heart disease、Movement、Vehicle、Artificial、Iris plant、Glass,包含不同的数据样本、条件属性和类别属性数目,已被广泛应用于数据挖掘领域。表1对这些数据集进行了简要描述。选择等宽(Equal-W)、等频(Equal-F)、Chimerge、MDLP、CAIM离散化方法进行对比分析。 表1 实验数据集描述 实验所用计算机处理器为Core i7、内存8 G,操作系统Windows7,编程环境为Matlab2010、Python3.7。 离散化后的数据集简化了信息的表示,减少了所需的存储空间,符合知识水平的表示,使得学习的过程更加准确和快速。因此,主要使用以下三个指标来综合衡量离散化方法的优劣。 (1)离散化后的区间总数。对于实际的离散化,最终形成的区间总数越小,离散化结果越简洁、效果越好。 (2)离散化后的精度。指离散化后数据相比原始数据的一致性程度,离散后的信息损失越少,离散化方法的精度越高。这一指标通过对离散化后的数据运行分类方法,计算分类的准确率来具体体现。 (3)方法运行时间。方法耗时体现了方法运行效率,对于动态离散化过程而言尤为重要。 实验中,首先对数据集分别运用6种离散化方法进行处理,记录离散化后的区间总数和方法运行时间,然后对离散化后的数据集运用5折交叉验证的方法,随机选取80%的数据作为训练集,20%的数据作为测试集,采用C4.5分类方法进行测试,得到分类的准确率,为消除误差实验重复5次,计算各指标的平均值作为最终评价标准。 3.2.1 离散化后的区间总数分析 由表2可知,DHCC方法离散后的平均区间总数最少,因为该方法的层次聚类部分能一次对所有属性进行聚类处理,属于全局离散化,同时结合正域的变化作为终止判断条件,可以避免分别对单个属性离散化所产生的不合理区间,平均排名得分1.4。Chimerge、MDLP离散化方法采用χ2统计量和信息熵作为区间划分的依据,对单个属性依次处理,属于局部离散化,最终所得区间总数有所增加,且随着设定的显著性水平增加,会对属性进行过度的离散化操作,产生大量的冗余区间。Equal-W、Equal-F方法通过经验公式设定初始的离散区间数,随着数据集的规模变大、属性增多,离散区间数也显著增加,平均排名得分为4.8、5.3。 表2 区间总数 3.2.2 离散精度分析 由表3可知,在测试的数据集中,DHCC方法的精度具有一定优势,测试精度的平均排名1.5分,表明DHCC方法在层次聚类和区间合并过程中,考虑所有条件属性、类别属性之间的相关性,有效减少信息损失,同时运用类别属性信息对相邻区间的合并进行有监督指导,最大限度地保留原始数据的一致性。Equal-W、Equal-F离散化方法的精度相比较低,主要是因为这两种方法都属于无监督,不使用类别属性信息,当数据分布不平衡时容易产生较差的区间,比如在Movement数据集中的测试精度只有47.5%和43.3%。Chimerge、MDLP方法属于有监督离散化,精度相比有所较高,但在离散化的过程中每次只考虑一个属性,忽视了属性之间的相互影响,平均精度比DHCC方法低。CAIM方法仅考虑最大类属性的样本,忽视了其他类属性的作用,使得在选择分割点时易出现误差,将具有不同分布的类别属性样本划分至同一个区间,降低分类的测试精度。 表3 离散精度Table 3 Discretization accuracy 3.2.3 运行时间分析 由表4可知,在测试的6个数据集中,Equal-W、Equal-F方法的运行时间最少,因为这两种方法在离散化时都不考虑类别属性信息,依据数据分布和经验公式进行区间划分,没有复杂的迭代计算过程。DHCC方法因为涉及层次聚类和相容度的计算、迭代合并操作,所需时间相对较长。Chimerge、MDLP、CAIM方法通过计算设定的离散化度量值,然后迭代进行合并、分割操作,在Artificial、Movement两个数据集的运行时间增加明显。 表4 运行时间 从实验对比分析可以得出,DHCC离散化算法在离散化后的区间总数、精度方面相比其他5种离散化算法具有一定优势,确保了离散化后的数据质量。 为验证所提离散化方法的有效性,以一个实际例子进行说明。表5为利用某型装备模拟训练系统进行射击训练时所涉及的部分数据决策表,具体属性包括军衔、装备操作等级、装备训练科目、装备训练次数、装备训练成绩等。 表5的数据表既包含连续型数据,又包含离散型数据。为从中挖掘装备训练规则,根据文中所提出的数据离散化处理框架和DHCC算法,对表5的数据进行离散化处理,生成离散化编码如表6所示。 表5 某型装备模拟训练系统数据决策表 表6 离散化编码表 根据离散化编码表对表5的数据进行离散化处理可得表7。 表7 离散化处理后的决策表 得到离散化后的数据后,采用经典的Apriori算法进行关联规则挖掘,设定支持度最小值为15%,置信度最小值为70%,以装备训练成绩作为关联规则后件,最终得到如下规则(“∧”表示属性取值条件同时满足,“⟹”表示由前项可推出后项)。 (1)X13∧X14∧X24∧X25∧X36⟹Y15,获得装备操作等级三级以上的下士、中士在“稳像模式下原地对不动目标射击”中获评成绩[90, 98]。通过了解该分队担负射击教学保障任务,对士官的等级评定要求严、抓得紧,保证了三级以上射手的装备训练水平达到规定的标准,也有利于形成射手的梯次配备,促进整体战斗力提升。 (2)X32∧X41⟹Y14∧Y15,表明“火控系统模式转换”科目通过较少次数训练后,评定分数位于[82, 89][90, 98]两个区间。这与实际情况相符,“火控系统模式转换”动作相对简单,训练对象能较快掌握要领,可适当减少训练次数。 通过某型装备模拟训练系统数据实现DHCC算法在实际装备训练中的应用,挖掘了装备训练科目、装备训练成绩等属性之间的关联,有助于提高装备训练效果。 构建了装备模拟训练系统数据离散化总体框架,提出了一种基于层次聚类和相容度的数据离散化方法,并应用于某型装备模拟训练系统数据分析,得出如下主要结论。 (1)离散化总体框架满足了装备模拟系统数据混合型决策表的处理需求,规范了系统数据预处理流程。 (2)动态确定簇数的层次聚类考虑属性相关性,实现了对各属性的初始划分,避免了人工指定阈值带来的误差。 (3)简化相容度差值合并相邻区间,能有效去除冗余划分,获得全局最优属性区间集合。
2 基于层次聚类和相容度的数据离散化方法
2.1 基于层次聚类的初始整体划分

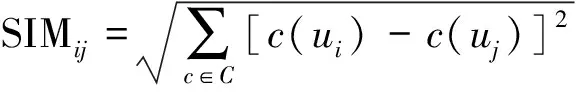

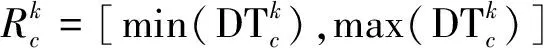
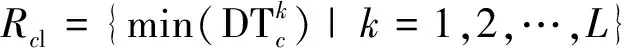

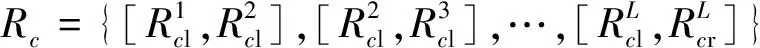
2.2 基于相容度的区间合并

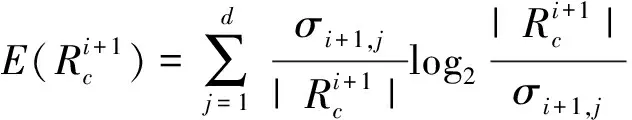

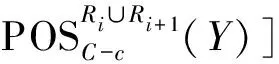
2.3 算法描述

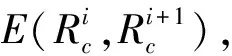
3 实验与对比分析
3.1 实验设计
3.2 实验结果分析
3.3 实例验证


4 结论
