基于海鸥优化改进采样过程的RBPF-SLAM算法

施振稳，张志安，黄学功，华 洪，陈冠星

(南京理工大学 机械工程学院， 南京 210094)

1 引言

随着科技水平的发展，移动机器人的智能化水平和自适应能力大大提升，如今在军事领域、工业领域、航天飞行领域以及日常生活和社会的各个层面都有着广泛的应用[1]。同时定位与建图(simultaneous location and mapping，SLAM)是移动机器人研究的热点问题，是机器人实现自主导航的关键环节。SLAM概念由文献[2]于1991年正式提出，指载体在未知环境中通过自身装备的传感器不断获取周围环境信息，构建周围环境的增量式地图，同时根据所构建的地图估计其位姿。早期，研究人员主要使用扩展卡尔曼滤波器(extended kalman filter，EKF)和粒子滤波器(particle filtering，PF)解决SLAM问题。然而EKF和PF算法都因效率低、计算复杂度大，无法很好满足SLAM实时性需求。为此，文献[3]提出基于Rao-Blackwellize粒子滤波器(rao-blackwellized particle filter，RBPF)的FastSLAM算法，将SLAM问题分解成机器机器人定位问题和基于已知机器人位姿的建图问题，解决了状态空间维数过高的问题，从而大大减少了计算量。然而传统的RBPF-SLAM方法必须用大量粒子才能很好地描述后验概率密度分布，但是粒子数越多，算法复杂度越高，导致效率低下，而且多数粒子在经过多次迭代后，其权值将不断减小，就会出现粒子退化问题。

针对传统基于RBPF粒子滤波SLAM方法的不足，国内外不少学者进行过研究。文献[4]基于FastSLAM提出一种名为Gmapping激光SLAM算法，该算法将高精度的激光测量数据加入到提议分布求取中，使提议分布更接近实际后验分布，从而提高算法的效率。文献[5-7]均尝试利用群智能算法优化RBP-SLAM算法，群智能算法与RBPF-SLAM算法结合的研究方兴未艾。海鸥优化算法(seagull optimization Algorithm，SOA)是文献[8]于2019提出的一种新颖的群智能优化算法，它通过模拟海鸥的迁徙和攻击行为来建立数学模型，可获得比粒子群优化等目前其他常见同类型算法具有更优的性能。本文将其引入PBRF-SLAM中，在采样过程中，每个粒子根据传播模型得到多个辅助粒子，再利用SOA的全局探测能力得到最优值作为此次的真实传播，从而避免优秀粒子因陷入局部极值而退化为噪声很大的粒子的情况。

对于RBPF-SLAM中出现的粒子退化问题，传统方法使用重要性重采样方法(sampling importance resampling，SIR)重新生成采样粒子，该方法尽管缓解了粒子退化问题，然而会破坏样本多样性。采样方差(sampling variance，SV)可以度量粒子分布在重采样前后的差异，从而可以评判重采样算法对粒子多样性的影响程度[9]。基于采样方差，文献[10]提出最小方差重采样方法(minimum sampling variance，MSV)，该方法可使重采样前后的采样方差最小化，并保护权值较小但更接近真实值的粒子不被删除，从而保证了重采样前后粒子的多样性。本文算法使用最小方差重采样方法替换原先的重采样方法并充分使用辅助粒子，进一步提高采样后粒子的多样性。

2 RBPF-SLAM算法

SLAM问题本质上是利用机器人获取的传感器数据去估计环境地图m和机器人轨迹x1∶t的后验概率p(x1∶t，m|z1∶t，u1∶t-1)的问题。在SLAM问题中有2个重要的数学模型：运动模型p(xt|zt-1，ut-1)与观测模型p(zt|xt，m)。运动模型表示给定上一时刻机器人的位姿xt-1和控制命令ut-1，机器人获得新位姿xt的概率密度；观测模型表示给定机器人位姿xt和地图m，传感器获得观测值zt的概率密度。

RBPF-SLAM关键思想就是将p(x1∶t，m|z1∶t，u1∶t-1)分解成如式(1)所示的轨迹估计和地图估计2个后验概率的乘积[11]：

p(x1∶t，m|z1∶t，u1∶t-1)=p(x1∶t|z1∶t，u1∶t-1)·

p(m|x1∶t，z1∶t)

(1)

其中:z1∶t代表机器人从1时刻到t时刻传感器获得的观测信息，u1∶t-1代表从1时刻到t-1时刻机器人的控制信息。

RBPF-SLAM算法的具体步骤如下：

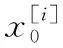
2) 采样过程。根据提议分布采样粒子。一般将机器人的里程计运动模型和传感器的观测模型相结合作为提议分布π，根据上一代粒子集χt-1生成下一代粒子集χt。在具体实现中，这个过程由两步实现，首先根据里程计运动模型获得粒子新的位姿，然后根据观测模型修正粒子的位姿。预测下一时刻的位置过程可以用下式表示：

(2)

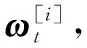
(3)

4) 重采样过程。粒子滤波的重采样步骤是重要的一步，但是过于频繁地重采样，将导致粒子快速贫化，为此在RBPF-SLAM中通过有效采样尺度标准来评判粒子集的优劣，确定何时进行重采样步骤，公式如下：

(4)

3 优化的RBPF-SLAM算法

3.1 海鸥优化算法

海鸥优化算法是一种仿生智能优化算法，其优化思想来源于海鸥个体间的迁徙和攻击过程。

1) 迁徙。在迁移过程中，该算法模拟了海鸥向一个位置移动到另一个位置移动过程。这个过程由3个步骤组成：避免碰撞、搜索者向最佳邻居的方向移动、保持与最佳搜索者的接近[12]。

步骤1避免碰撞：避免海鸥个体之间的相互碰撞。引入一个变量A用于计算新的搜索位置：

(5)

(6)

其中： 引入fc变量控制变量A的值，变量A由fc线性减少到0。

步骤2搜索者向最佳邻居的方向移动：在避免了邻居之间的碰撞后，搜索者根据式(6)向最佳邻居的方向移动：

(7)

B=2×A2×rd

(8)

其中rd为[0，1]之间的随机数。

步骤3保持与最佳搜索者的接近：最后搜索者需要根据最佳搜索者更新其位置：

(9)

2) 攻击。海鸥在迁徙过程中会不断地改变攻击的角度和速度，当攻击猎物时，将进行空中的螺旋运动，该运动可描述为：

x′=r×cos(k)

(10)

y′=r×cos(k)

(11)

z′=r×k

(12)

r=u×ekv

(13)

其中：r是每一圈螺旋半径的大小，k的范围为0≤k≤2π。u和v是定义螺旋形状的常数，e是自然对数底。

(14)

在海鸥优化算法中需要一个适应度函数计算每只海鸥个体的适应度值。在激光SLAM中可以根据机器人在全局标系下的估计位姿，将当前扫描的激光雷达数据点逐一映射到全局地图中得到测量似然域，而后根据测量似然域和全局地图的匹配程度来评价估计位姿的好坏[12]。将评价似然域和全局地图的匹配程度的计算函数作为海鸥优化算法的适应度函数：

(15)

其中，S为匹配得分，bm,i表示激光束i在全局坐标系下所对应的栅格，mp,i为全局地图中距bm,i最近的占用栅格，Gs表示高斯系数，Dis函数表示求2个栅格的距离，N表示激光雷达的总激光束数。

将海鸥优化算法应用到RBPF-SLAM的采样过程中。为避免优秀粒子因采样的随机性退化为噪声很大的粒子的情况，每个粒子从运动模型采样时均采样B个粒子，本文中称这些粒子为辅助粒子。然后将这些辅助粒子作为海鸥个体，进行迭代寻优，将其中的最优值作为本次采样的结果，这个过程可以用下式表示：

(16)

其中n为辅助粒子的序号。

3.2 优化重采样策略

在传统RBPF-SLAM重采样过程中，采用轮盘赌法来选择被保留的粒子，从而使得大权重的粒子更有可能被复制，小权重的粒子更有可能被去除。然而，这种根据权重随机地复制和去除粒子的方式，容易导致粒子多样性丧失，在SLAM过程中产生定位失真、回环时无法保证建图一致性等现象。针对这一问题，使用最小方差重采样方法来替换RBPF-SLAM中简单、粗糙的重采样策略，并且为了进一步提高粒子集的多样性，在选择粒子时根据重采样计数选择辅助粒子代替重复复制的粒子。本文使用的重采样方法步骤如下：

步骤1为每个粒子i设置一个重采样计数C[i]，并初始化为0。

C[i]=floor(Mω[i])

(17)

其中，floor函数表示向下取整，M为粒子总数：

(18)

步骤3计算所有粒子的重采样计数总数：

(19)

步骤5根据每个粒子的重采样计数C[i]，选择匹配得分最高的C[i]个辅助粒子进行复制。

整体的算法流程如下：

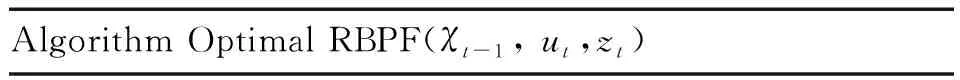
Algorithm Optimal RBPF(χt-1, ut,zt)

fori=1 toMdo

//Generate samples from the transtion model

forn=1 toBdo

end for

end for

//calculate the importance weight

ωt← calWeight(xt,zt,mt-1)

//update particle set

ifNeff<1/2 then

χt← MSV resample(χt)

end if

//Update map

mt← registerScan(mt-1,xt,zt)

4 仿真实验

为了验证优化算法的有效性，采用Gmapping算法作为对照进行仿真实验，算法来源于https//svn.open—slam.org[13]。仿真实验所用的计算机，处理器为英特尔酷睿i7-10750H，6核，主频为2.6 GHz，内存为16 GB，使用Ubuntu16.04操作系统。公开数据选用集Intel Research Lab和ACES Building数据集，这两者均以Carmen格式保存了机器人运行一定时间内的激光雷达和里程的全部测量数据以及相应的时间戳。为了使得实验结果具有可对比性，使用同一个数据集时，算法的所有参数的设置都相同。通过比较两种算法的定位效果和所建地图与基准地图的差异程度来评价两种算法的优劣。对于定位效果的定量对比，本文使用文献[14]提供评估工具metricEvaluator，该工具可通过输入SLAM算法得到机器人的轨迹信息机器人真实轨迹信息(Ground Truth)来计算总体的定位误差，定误差的计算公式如下：

(20)

图1采用的是Intel Research Lab数据集，该数据集为经典的室内环境，环境大小约为28 m×28 m，内部有较多的特征。由仿真结果可知，在5个粒子的情况下，2种算法均能构建出较好的地图，但可以看到Gmapping算法在黑框处出现明显的重影现象，且整体的定位误差较大[15]。

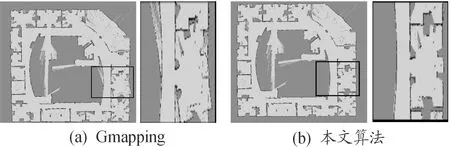
图1 Intel Research Lab 数据集仿真实验结果图Fig.1 Simulation experiment results of Intel Research Lab

图2采用的是ACES Building数据集，该数据集为走廊环境，环境大小约为50 m×50 m，环境规律整洁但是特征较少，且机器人运动的轨迹中构成较多的回环，通过多次实验，不断逐渐增加粒子数，由仿真结果可知，在20个粒子的情况下，本文算法已经可以构建出一致性较好地图，Gmapping算法所构建的地图仍有多处出现地图不一致的情况。

图2 ACES Building数据集仿真实验结果图Fig.2 Simulation experiment resultsofACES Building

表1记录了用metricEvaluator评估工具计算的2次仿真结果的定位误差。定位误差由平移误差和旋转误差两部分组成，计算工具的计算结果包含了误差的平均值和标准差。从计算结果可以看出对于2个数据集本文算法的定位效果均有明显提升。其中Intel Research Lab数据集总体平移误差的平均值减少了36.36%，总体旋转误差的平均值减少了33.33%。ACES Building数据集总体平移误差的平均值减少了41.67%，总体旋转误差的平均值减少了40%。

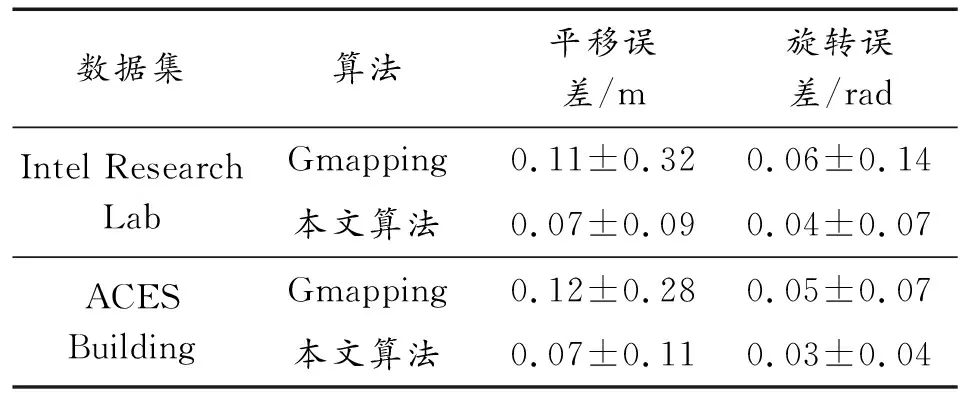
表1 定位误差

5 实体测试

图3是本文算法的实验平台，该平台采用四轮差分驱动，并搭载有4个光电编码器和思岚A1激光雷达。实验环境为某科技园办公楼的日字形的走廊，部分实验环境如图4所示。

图3 实验平台图Fig.3 The experimental platform

图4 部分实验环境图Fig.4 Part of the experimental environment

对于实际的机器人实验，由于难以采集到机器人真实轨迹信息，因此不能通过定量计算误差来衡量地图准确度。虽然单单通过直观地对比构建地图的方法具有一定的局限性，但是通过对比用相同粒子数目生成的环境地图与真实环境的相似程度，还是可以定性地评判算法的优劣。如图5所示，同为30个粒子的情况下，本文算法所构建的地图于实际的建筑的一致性更好，并且没有因为回环时粒子多样性不足而出现明显的重影的现象。

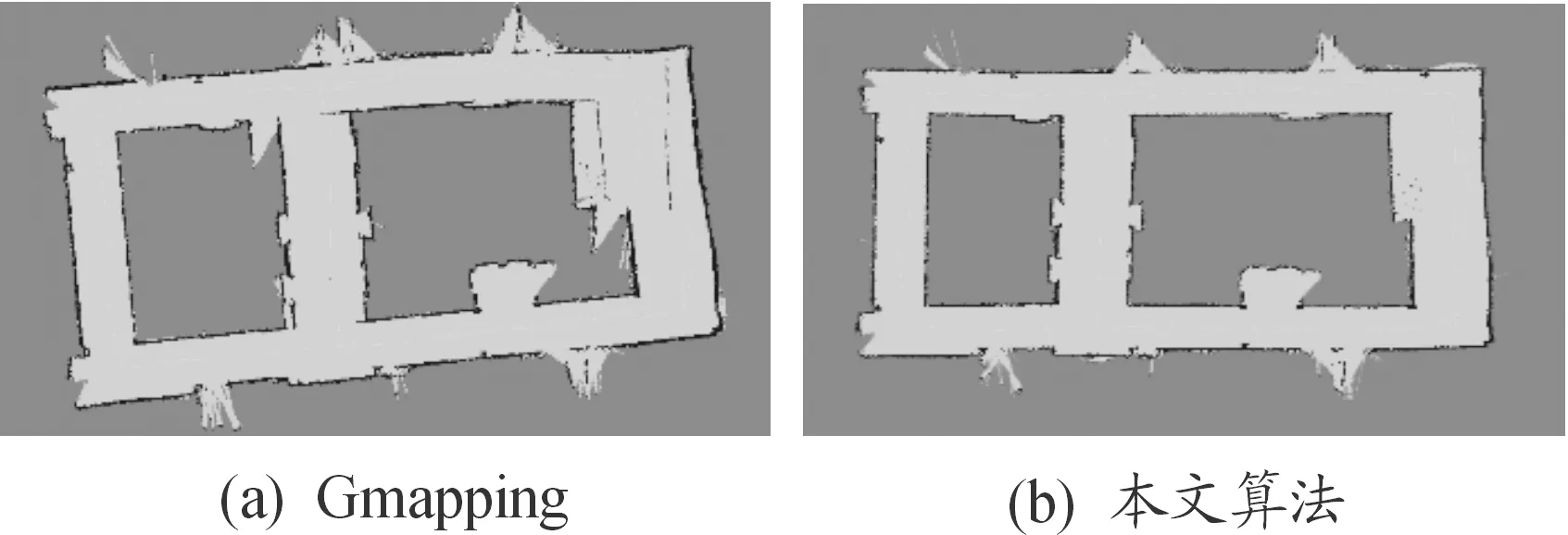
图5 生成的栅格地图Fig.5 TheComparison of generated grid map

6 结论

1) 在传统RBPF-SLAM算法基础上，利用海鸥优化算法改善RBPF的粒子采样过程，从避免了优秀粒子退化为噪声很大的粒子的情况。

2) 优化后的RBPF-SLAM取得了更好定位和地图构建的效果，相比于Gmapping算法，总体的平移误差的平均值分别降低了36.36%和41.67%，总体的旋转误差的平均值分别降低了33.33%和40%。

3) 室内结果表明优化后的算法能够完成构建地图的任务且能获得与实际环境一致性更好的地图。