一种圆轨道航天器外热流通用计算方法
2021-10-15易桦黄兴江海
易桦 黄兴 江海
(北京空间飞行器总体设计部 空间热控技术北京市重点实验室,北京 100094)
航天器在空间轨道运行所受到的空间外热流对航天器热设计有重要影响,在航天器热设计初期一般都必须进行外热流分析,以决定航天器热设计顶层方案和航天器热分析的极端工况。空间外热流包括太阳直射热流,行星反照热流和行星红外热流等。由于太阳为平行光,太阳直射热流只需要考虑行星的遮挡,相对容易分析;但是行星红外和行星反照需要考虑航天器与行星之间的位置关系,行星反照还需要额外考虑行星表面受照情况,计算过程非常复杂。早期由于计算机软硬件的限制,国内外主要采用对不同积分域进行积分的方法,对不同输入参数需进行查图表来获得行星红外和行星反照[1],但积分域的确定过程十分复杂,而图表只能给出部分典型参数对应的结果,局限性较大。随着计算机技术的高速发展,国内陆续提出了通过蒙特卡洛(Monte Carlo)随机模拟法[2-4]等求行星红外和行星反照的方法,这些方法求行星反照时还需要将行星中心到太阳矢量与航天器表面法线在局部球坐标系的经度差作为输入,却未给出求经度差的通用方法,无法满足当前日益复杂的工程应用需求。文献[5-7]应用积分方法,对太阳同步轨道、倾斜轨道在对地姿态的外热流进行了分析,文献[8]用平均模拟法对月球红外辐射进行了精细计算,但这些方法都是针对特定的某种轨道和姿态进行分析,通用性不足,且部分方法仍采用基于相角的简化方法[9]求行星反照,准确度不够。
本文基于轨道坐标系到天球坐标系的转换矩阵,提出了一种圆轨道航天器外热流通用计算方法,采用解析法计算太阳直射热流,将行星可视球冠划分为等面积微元,采用数值积分法求解行星红外和行星反照,无需求解行星中心到太阳矢量与航天器表面法线在局部球坐标系的经度差,能有效简化计算过程;并将该方法应用于典型案例上,与热分析软件计算结果进行对比。
1 圆轨道航天器外热流计算方法
首先定义天球坐标系为全局坐标系,轨道坐标系为局部坐标系。定义Ω为升交点赤经,i为轨道倾角,f为真近点角,ω为近地点幅角。
天球坐标系可以按以下步骤旋转到轨道坐标系:先绕+Z轴旋转Ω,再绕+X轴旋转i,再绕+Z轴旋转f+ω+π/2,最后绕+X轴旋转-π/2。因此,轨道坐标系到天球坐标系的转换矩阵为
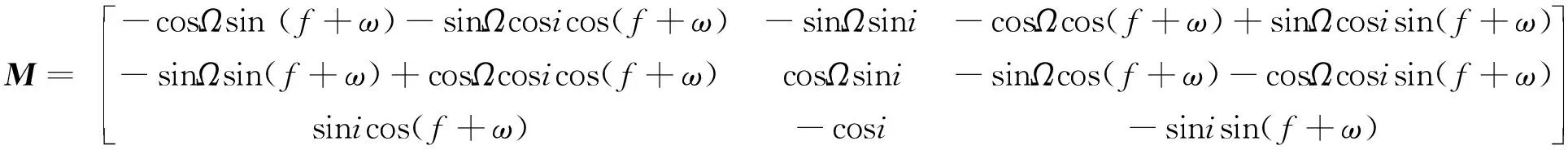
(1)

1.1 太阳直射热流计算
光照期(f≤fin或f≥fout)航天器表面太阳直照热流qSUN为
(2)
式中:S为太阳辐照强度;I为黄赤交角;Φ为太阳黄经;fin和fout为从近地点算起的进阴影和出阴影位置的真近点角,可按文献[9]求解。
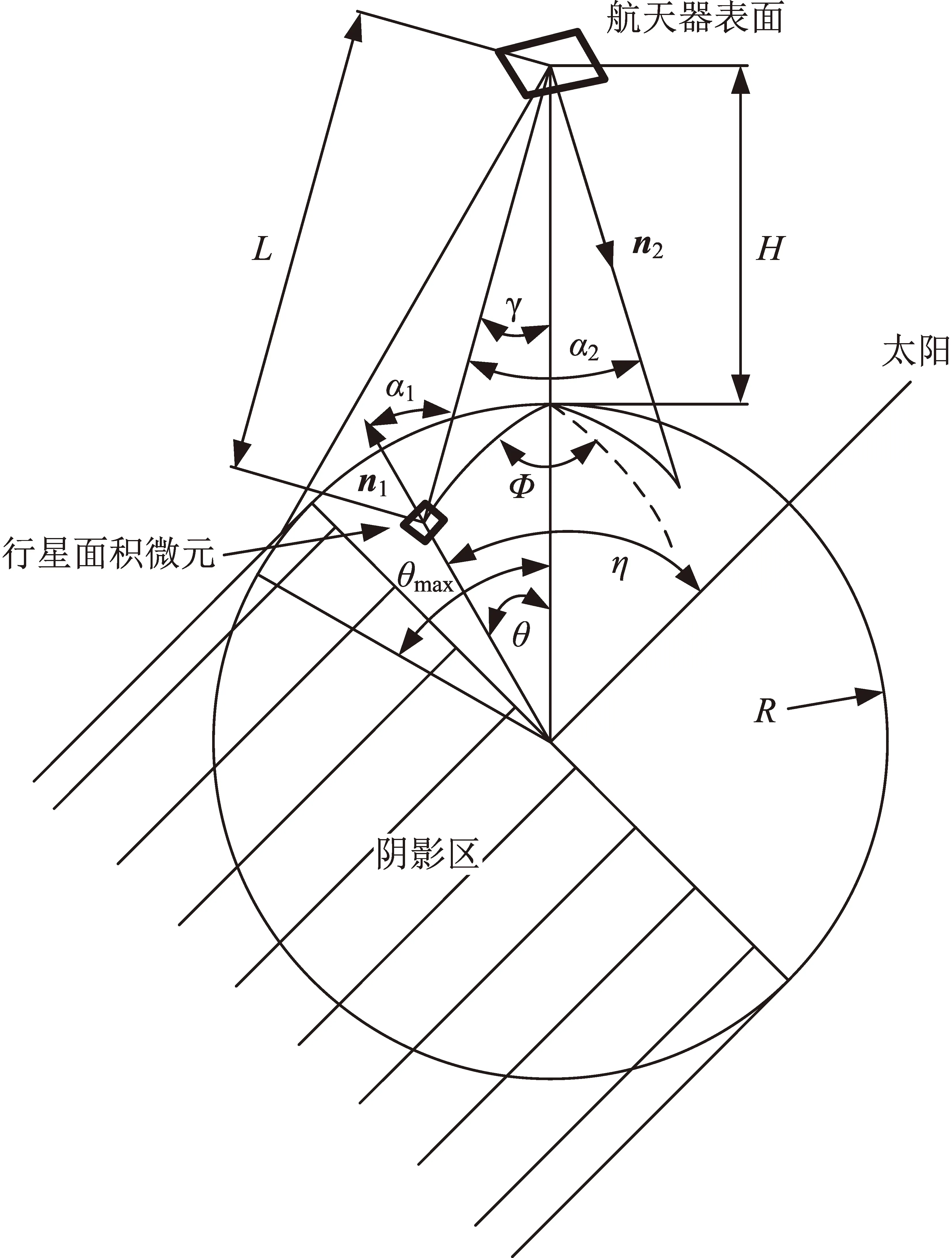
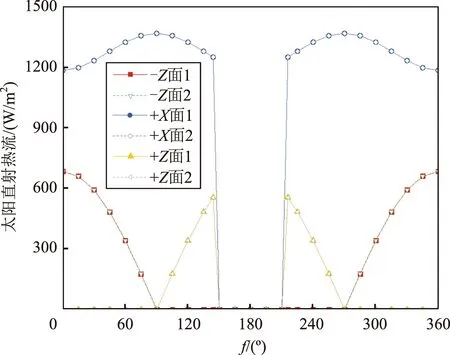
阴影区(fin 图1 行星红外和行星反照热流的计算Fig.1 Calculation of planet infrared and albedo heat flux 航天器表面行星红外热流qIR和行星反照热流qAL为[1,4] (3) (4) 式中:ρ为行星反照率;α1为行星面积微元法线(行星中心到面积微元的矢量)和面积微元到航天器矢量的夹角;α2为航天器表面法线和航天器到行星面积微元矢量的夹角;η为行星面积微元法线和行星中心到太阳矢量的夹角;L为行星面积微元到航天器的距离。 考虑到随机方法[4]在微元划分数量较小的时候相对不准确,本文使用等面积平均数值积分方法,以每个行星可视局部球冠表面微元的面积相等为原则,按θ和φ分别划分为m1和m2份,θ和φ取在面积微元的中心值。则 (5) (6) (7) 因此,航天器表面行星红外热流qIR为[1,4] (8) 航天器表面行星反照热流qAL为[1,4] (9) (10) (11) 与文献[1,4]需要将行星中心到太阳矢量与航天器表面法线在局部球坐标系的经度差作为输入不同,本文提出cosα2和cosη的计算方法如下: (12) (13) 式中:γ为航天器到面积微元矢量与航天器到行星中心矢量的夹角。 (14) 需要说明的是,本方法同样适用于对可视行星球冠进行随机分割的情况,分割份数越大,计算结果越接近;另外,本方法只适用于凸表面,不适用于凹表面。 本文充分考虑到圆轨道的特性,为进一步简化计算,定义一种特殊圆轨道如下:i=β(阳光与轨道面的夹角),Ω=π/2,ω=-π/2,Φ=0。对于标准开普勒圆轨道,只需要求出β角,并将该特殊圆轨道计算出的外热流结果进行-Λ(会日点到近地点角距)相位调整即可,对于周期平均值,由于和相位无关,标准开普勒圆轨道和特殊圆轨道计算结果相同。 考虑到大部分航天器姿态为对地定向、对日定向、偏航姿态或上述姿态的组合,本文针对上述姿态的特殊圆轨道,以六面体各个面为典型表面进行外热流分析。 对于不同姿态,六面体各个表面法线方向不同,因此太阳直射热流和cosα2有所不同,具体如下。 对地定向姿态定义与轨道坐标系相同,即+Z轴对地,+X轴为飞行方向,+Y为轨道面负法线方向。 各个面光照期qSUN和cosα2如表1所示。 表1 对地定向姿态六面体各个面的光照期太阳直射热流和cosα2Table 1 Solar incident heat flux during illumination and cosα2 value of cube’s six sides in +Z pointing nadir attitude 对日定向姿态定义为:-Z轴对日,+X轴为行星中心到太阳矢量与轨道面法线方向的叉乘,+Y由右手定则确定。对于-Z面,光照期qSUN=S;对于其他面,光照期qSUN=0。各个面的cosα2如表2所示。 表2 对日定向姿态六面体各个面的cosα2Table 2 The cosα2 value of cube’s six sides in -Z pointing sun attitude 偏航姿态定义为:+Z轴对地,+Y轴为+Z轴和行星中心到阳光矢量的叉乘,+X根据右手定则确定。按照上述定义求得偏航姿态局部坐标系到对地定向局部坐标系的转换矩阵为 (15) 因此,各个面光照期qSUN和cosα2如表3所示。 表3 偏航姿态六面体光照期各个面的太阳直射热流和cosα2Table 3 Solar incident heat flux during illumination and cosα2 value of cube’s six sides in yaw attitude 根据上述计算方法,编制了计算程序。本文以β=60°,H=600 km的上述特殊圆轨道为例,取S=1367 W/m2,ρ=0.3,m1=m2=100,将一个周期划分为24个点,对偏航姿态外热流进行分析。 -X和±Y面太阳直射热流始终为0,其他表面的太阳直射热流见图2。-Z面行星反照热流始终为0,其他表面的行星反照热流计算结果如图3所示。行星红外不随时间变化,其计算结果如表4所示。上述图2、图3中,末尾的1和2分别代表采用本文方法编制的程序计算结果和采用蒙特卡洛方法的Thermal Desktop热分析软件计算结果。 图2 太阳直射热流分析结果对比Fig.2 Comparison of incident solar heat flux 图3 行星反照热流分析结果对比Fig.3 Comparison of the albedo heat flux 表4 行星红外热流分析结果对比Table 4 Comparison of the infrared heat flux W/m2 本方法计算结果与软件计算结果的对比表明: (1)太阳直射热流绝对误差不超过0.1 W/m2,相对误差不超过0.02%; (2)行星红外和行星反照热流绝对误差不超过2 W/m2,相对误差不超过3%(绝对值大于2 W/m2时)。 以上对比结果充分说明了本方法的准确性。本方法编制的程序运行时间为秒级,与热分析软件相当;此外,与热分析软件相比,本程序无需建模,只需要输入少量参数和待求表面法线单位矢量,操作简单,准确度和运行效率均能较好地满足外热流分析工作的需求。 本文提出了一种圆轨道航天器外热流通用计算方法,采用解析法计算太阳直射热流,采用数值积分法求解行星红外和反照,无需求解行星中心到太阳矢量与航天器表面法线在局部球坐标系的经度差,能有效简化计算过程。基于此方法,选取一种特殊圆轨道,对常用姿态(+Z对地,-Z对日,基于+Z对地的+X对日偏航)六面体卫星的瞬态外热流进行分析,并将偏航姿态外热流分析结果与热分析软件计算结果进行了对比。对比结果表明:本方法计算的瞬态外热流结果与软件计算结果相差不超过2 W/m2,相对误差不超过3%(绝对值大于2 W/m2时),充分说明了本方法的准确性。本方法能快速计算圆轨道航天器常用姿态外热流,为航天器热控设计和热分析提供重要依据,可以应用于各领域航天器,通用性和扩展性好,准确度和运行效率高,能较好地满足实际工程应用需求。1.2 行星红外和行星反照热流计算
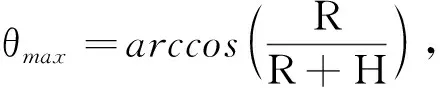
2 本方法典型应用案例
2.1 对地定向姿态

2.2 对日定向姿态
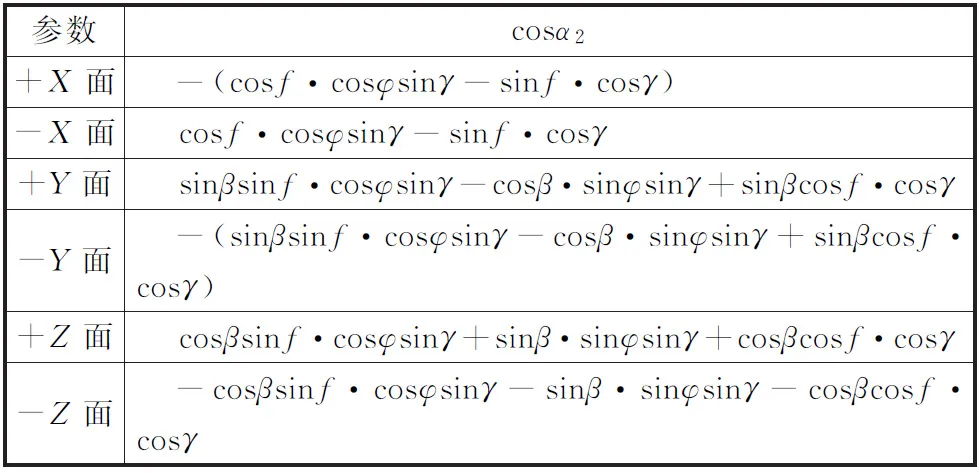
2.3 偏航姿态
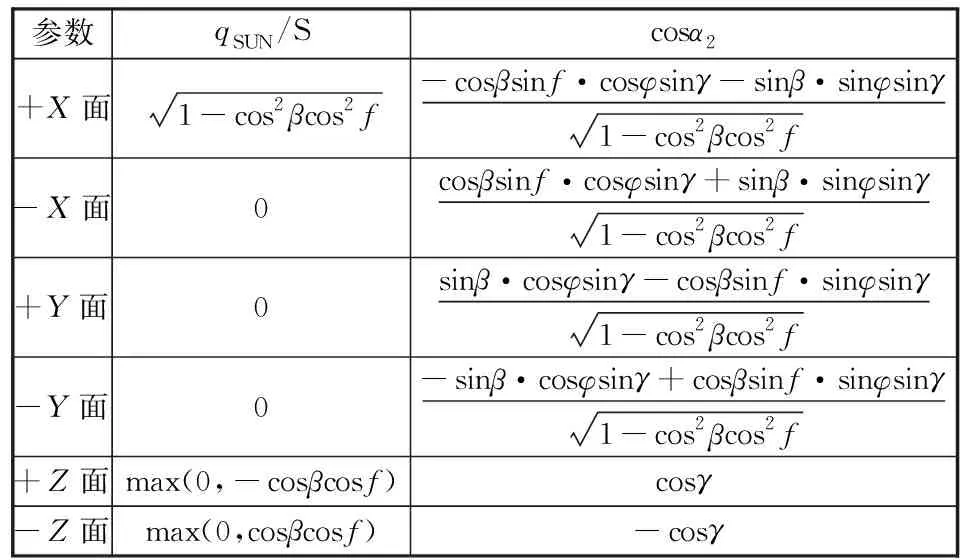
3 计算结果与验证



4 结束语
