机械臂初始构型对航天器姿态干扰力矩的影响研究
2021-10-15尹旺王翔
尹旺 王翔
(北京空间飞行器总体设计部,北京 100094)
由于空间机械臂能代替航天员在复杂的太空环境中方便可靠地执行一系列任务,因此世界各航天大国陆续开展了对空间机械臂的研制,随着中国空间站任务的迫切需求,我国也开展了空间机械臂的研制工作[1]。
为保持无线通信通畅和保持对地姿态,航天器通常情况下有定向稳定要求。由于机械臂和基座之间存在动力学耦合效应,因此空间机械臂在运动时对航天器产生的基座反力会成为姿态扰动力,一方面反作用飞轮的控制力矩有上限,另一方面持续的姿态扰动可能会引起反作用飞轮的饱和,飞轮饱和后需要姿控发动机进行喷气卸载,而发动机的控制力矩较大,为避免关节受到损坏,因此在喷气过程中要求机械臂处于停控状态,这势必会增长机械臂的任务时长,这也是减少反力、减少扰动的意义。于是人们希望通过轨迹规划的方式使机械臂在完成规定操作的同时对平台产生的反作用最小,多数研究者都是在关节空间对机械臂的路径进行规划[2-5],虽然方法的有效性得到了验证,但是此类方法只适用于空间点到点的任务情景。当机械臂末端需要进行直线或圆弧轨迹跟踪时,应在笛卡尔空间对机械臂的路径进行规划。目前机械臂在笛卡尔空间的轨迹规划主要还是基于速度级的逆运动学,文献[6]利用机械臂的冗余度,对关节力矩和操作灵活性进行了综合优化,文献[7]基于粒子群算法对冗余机械臂的自运动项进行了优化,从而使关节的驱动力矩能耗达到最优,但是自运动项的优化能力有限,并不能充分发挥冗余机械臂的优势。
基于速度级逆运动学得到机械臂各关节速度之后,需要对关节角速度进行数值积分才能得到各关节的角位移,而进行数值积分的前提是需要给定七个关节的初始角度值,七关节的初始角也称为机械臂的初始构型,由于七自由度机械臂存在冗余性,非奇异状态下的机械臂有无数多种构型[8]。当机械臂末端需要沿着某一条路径进行运行时,基于不同的初始构型进行轨迹规划,航天器平台受到的反作用也大小不一。因此,针对任何一种任务需求,本文期望通过对比分析得出机械臂最优的初始构型,动作之前,将机械臂调整为最优构型,能大大减小其在运行过程中对航天器产生的姿态干扰,同时使机械臂的操作效果更好。
1 七自由度机械臂模型的建立
机械臂的运动状态依赖于轨迹规划时初始构型的选择,所以机械臂运动产生的反力也与初始构型密切相关。因此,建立七自由度机械臂运动学及动力学模型是后续分析研究的理论基础,得到机械臂的运动学及动力学模型后,即可揭示机械臂在运动过程中对平台产生的反作用与机械臂初始构型之间的关系,基于此,寻求使基座反作用达到最小的初始构型。
1.1 正运动学建模
根据Denavit和Hartenberg[9]提出的方法(D-H参数法)建立七自由度机械臂的坐标系及正运动学方程,机械臂的基坐标系{0}和各连杆的固连坐标系{i}如图1所示(i= 1, 2, …,7),其中,各坐标系的z轴与关节轴共线,x轴与连杆的公垂线重合,y轴根据右手法则确定。

图1 空间机械臂运动学模型Fig.1 Kinematic model of space manipulator
由D-H参数法知:4个参数可唯一确定相邻连杆之间的变换通式,七自由度机械臂的D-H参数如表1所示。其中,li是从zi到zi+1沿xi测量的距离,代表着连杆i的长度;αi是从zi到zi+1绕xi旋转的角度,代表连杆i的扭角;di是从xi-1到xi沿zi测量的距离,表示相邻两连杆之间的偏置;θi是从xi-1到xi绕zi旋转的角度,表示相邻两连杆之间的转角。
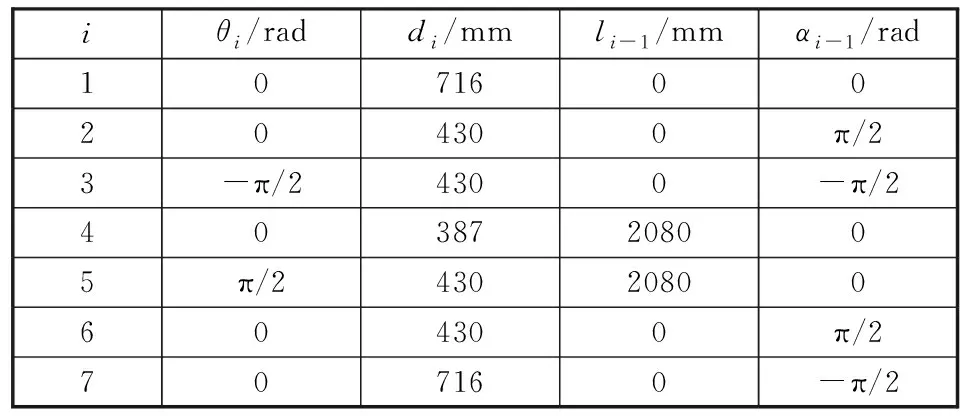
表1 七自由度机械臂的D-H参数Table 1 D-H parameters of 7-DOF manipulator
(1)
式(1)即为机械臂系统的运动学方程,表示机械臂末端相对基座的位姿与机械臂七个关节角变量θ1,θ2,…,θ7之间的关系,机械臂末端位姿可由七个关节角唯一确定。
1.2 逆运动学建模
速度级逆运动学是根据机械臂末端的广义速度求解关节空间的角速度,而机械臂的雅克比矩阵可以将关节空间的速度线性映射到末端的操作速度

(2)

七自由度冗余机械臂在操作空间有无穷多个逆解,由矩阵理论知式(2)的逆解为
(3)

J+=JT(JJT+λ2I)-1
(4)
变阻尼系数λ为
(5)
式中:λ0称为最大阻尼系数;σ为雅克比矩阵的最小奇异值,σ0为最小奇异边界值。
位置级逆运动学是根据机械臂末端位姿求对应的各个关节角,本文通过关节角参数化方法求偏置式七自由度机械臂逆运动学,给定关节1的角度值,可以获得8组逆解,由于本文和文献[8]中机械臂的初始构型有差异,对于同一末端位姿,本文和文献[8]中逆解之间的关系为
(6)
1.3 动力学建模
保持坐标轴方向不变,将图1中坐标系平移到各连杆的质心处即可得到机械臂系统的质心坐标系,根据多体系统运动学理论[10]求各连杆的绝对角速度和角加速度分别为

(7)

(8)

β=-(pT)T
(9)
σ=-TTh
(10)
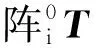
(11)
机械臂系统各连杆的质心速度和加速度可表示为
(12)
(13)

根据式(9)~式(13)求得的角速度、角加速度、质心速度和质心加速度矢量都是在基坐标系中表示的,需要通过相应的变换矩阵将其转换到自身坐标系下。
根据牛顿-欧拉方程得到各连杆在运动过程中产生的惯性力和惯性力矩分别为
(15)
式中:mi和ciIi为机械臂系统第i个连杆的质量和相对质心的惯性张量。递推(i:7→1)得到七自由度机械臂的逆动力学方程为
(17)
式中:ifi和ini分别为连杆i-1对连杆i的力和力矩在连杆坐标系{i}中的表示,irci表示连杆i的质心在自身坐标系下的位置矢量,-0f1和-0n1表示机械臂对航天器平台的反作用力和力矩,当机械臂末端空载时,i+1fi+1=i+1ni+1=0。
2 基座反作用求解程序
当机械臂的末端要求按照预先设定好的路径进行运动时,需要采用笛卡尔空间的轨迹规划方法,为保证机械臂运行过程中的连续性和平稳性,末端速度采用基本的梯形速度曲线进行规划。首先基于不同的初始构型规划出各关节相应的运动状态,然后根据各关节的运动状态求解基座所受的反作用力矩,分析比较得出机械臂的最优初始构型,具体的算法实现过程如图2所示。
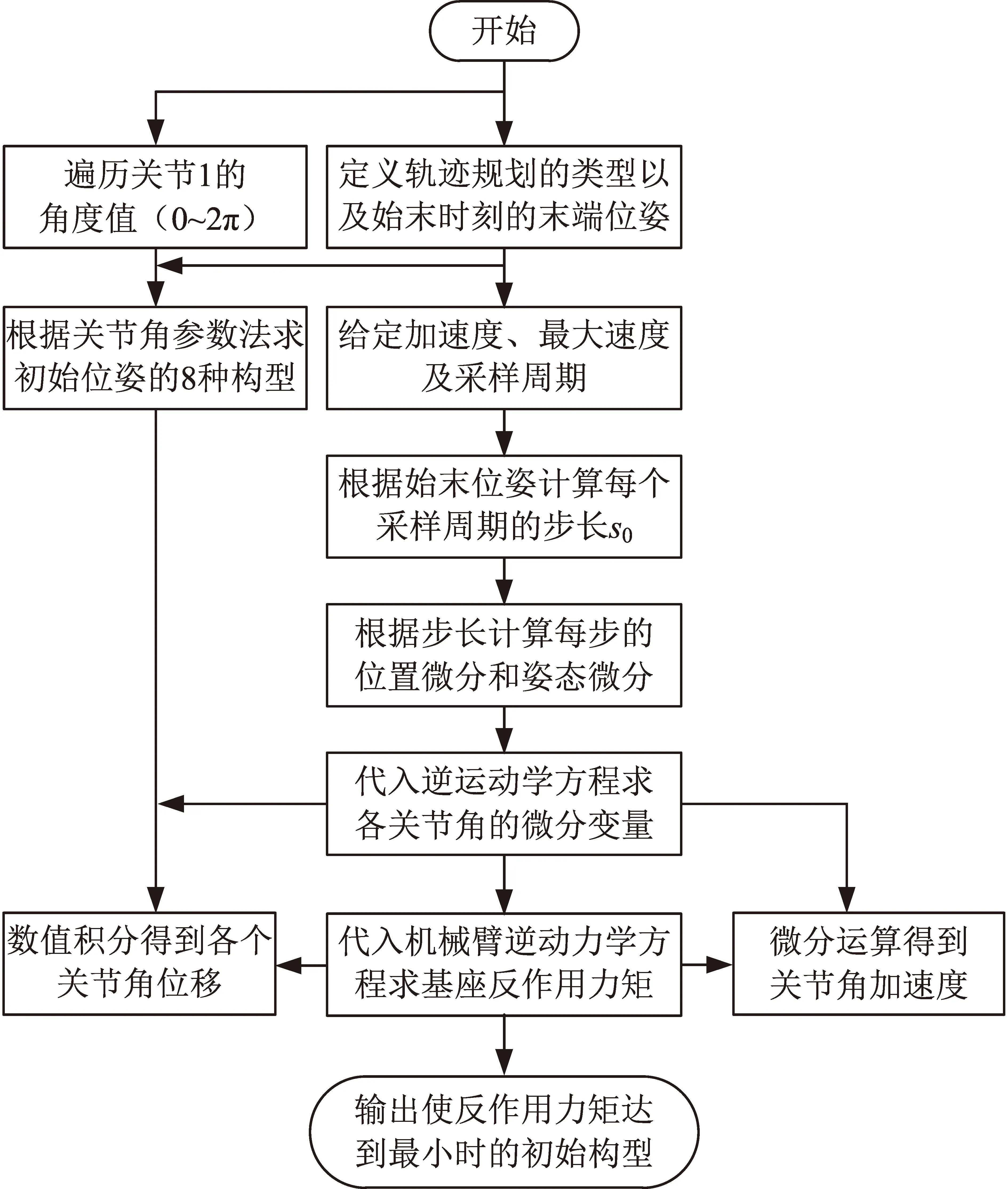
图2 机械臂基座反作用求解过程Fig.2 Process of solving the base reaction of manipulator
3 仿真分析
3.1 参数设置
假设机械臂末端由起点(-2,-2,2)到终点(-1.5,-1,1)做直线运动(相对于基坐标系{0}),同时运动过程中机械臂的姿态始终保持不变,仿真时长为11.5 s,共575步。运行过程中机械臂末端在基座坐标系下的姿态矩阵为
(18)
式中:R0和Rd分别为起始时刻和结束时刻的姿态矩阵。
七自由度机械臂的质量特性参数参见文献[5],本文针对负载为0 kg、300 kg和3000 kg的3种不同工况,研究机械臂在不同的初始构型下沿着直线运动对基座产生的反作用大小,假设将机械臂末端的负载视为附加在连杆7质心处的质量块,且不考虑转动惯量的影响。由上文知机械臂的初始构型与关节角1的选取密切相关,当关节角1给定时能求出八组逆解。采用枚举法令关节角1在0~2π之间取值,间隔为0.1 rad,因此能够得到512组计算结果。此处以基座反作用力矩(3个方向的合成)的最大值作为评价反作用大小的标准,即
(19)
3.2 结果分析
对于末端负载300 kg的工况,按以上程序计算所有初始构型下机械臂产生的反作用力矩,对512组计算结果对比分析发现:当机械臂的初始构型为[-0.48 -0.07 -2.55 1.35 -3.03 4.68 -3.20]T时,对基座产生的反作用峰值力矩达到最大为39.74 Nm,将此构型记为构型1,基于构型1进行直线路径规划时各关节的角位移和角速度如图3所示。


图3 基于构型1的轨迹规划Fig.3 Trajectory planning based on configuration 1
当机械臂初始构型为[3.80 0.01 -5.14 -1.28 1.05 1.56 -0.01]T时,反作用力矩峰值达到最小为18.16 Nm,将此构型记为构型2,基于构型2进行路径规划得到的关节运动状态如图4所示。


图4 基于构型2的轨迹规划Fig.4 Trajectory planning based on configuration 2
两种初始构型下的基座反作用力矩对比如图5所示,对比发现,按照两种初始构型对机械臂进行路径规划时,两者在笛卡尔空间的轨迹是完全一样的,但是在运动过程中机械臂的构型却大不相同,对基座产生的反作用峰值力矩相差近50%,且构型1对应的关节角速度远大于构型2。仿真表明,按照初始构型2进行轨迹规划的效果优于构型1。图6和图7分别为基于构型1和构型2规划的直线轨迹。
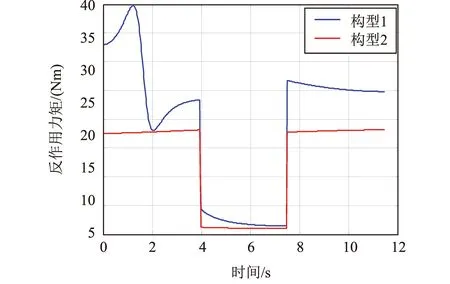
图5 两种初始构型下的基座反作用力矩对比Fig.5 Comparison of base reaction moments under two initial configurations

图6 基于构型1规划的轨迹Fig.6 Trajectory planning based on configuration 1
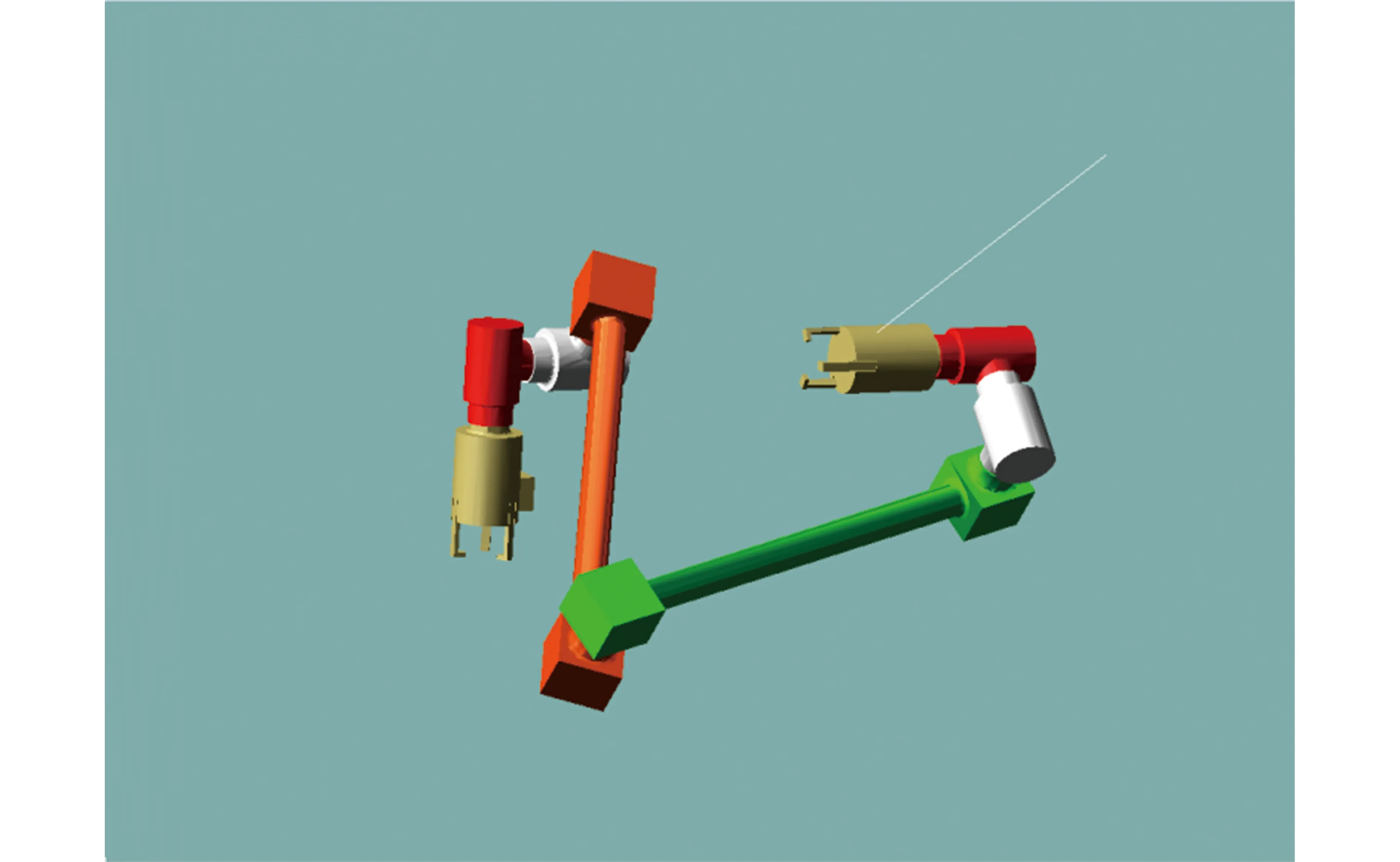
图7 基于构型2规划的轨迹Fig.7 Trajectory planning based on configuration 2
对于零负载和3 t负载的情况,同样按照本文第2节所述的流程进行计算,仿真结果表明分别基于构型1和构型2进行规划会使反作用力矩峰值达到最大和最小,两种构型下基座受到的反作用力矩如图8所示。对于固定基座和同样的速度曲线,不同质量的负载只会引起负载惯性力的变化,将其解算至各关节然后叠加空载关节力矩,递推可得到基座的反作用力矩,因此无论末端负载多大,基于构型2进行规划产生的反作用力矩峰值均小于构型1。


图8 不同初始构型下的基座反作用力矩比较Fig.8 Comparison of base reaction moments under different initial configurations
4 结束语
基于不同的初始构型对七自由度空间机械臂进行了直线规划,研究了机械臂初始构型对基座反作用力矩的影响。通过仿真得出的结论为:①对于笛卡尔空间的某一条规划轨迹,通过调整机械臂的初始的构型,能大幅减小机械臂在运行过程中对基座产生的反作用力矩。当机械臂末端负载分别为0、300 kg和3 t时,通过调整初始构型能使航天器平台受到的反作用力矩峰值减小88%、54%和11%。②在工程实际中,根据本文方法能够在机械臂无数的初始构型中找到一种最优的构型,基于此构型进行笛卡尔空间的轨迹规划时,使得机械臂在运动过程中航天器平台受到的反作用力矩峰值最小,因此减小了干扰力矩超出反作用飞轮控制力矩从而造成航天器姿态失控的风险。
