“正弦函数、余弦函数的图象”的教学设计

黄诗贤

◆摘  要：本文就“正弦函数、余弦函数的图象”进行教学设计，并就教学设计进行反思。

◆关键词：图象;教学设计;核心素养

“正弦函数、余弦函数的图象”是一节概念课，本节课的教学应该要引导学生经历知识的完整生成过程，体现了课堂结构的严谨性与知识间的逻辑连贯性，具体设计如下。

内容和内容解析

本节课是在前面已学过一次函数、二次函数、指数函数、对数函数，此前还学过三角函数的概念及诱导公式的基础上，来学习来正弦函数、余弦函数的图象画法，为今后研究正切函数以及函数y=Asin（[ω]x+[φ]）的图象的知识奠定良好基础。本节课的教学重点是正弦、余弦函数图象的作法。本节课涉及了逻辑推理、直观想象等数学学科核心素养。

目标和目标解析

1.用几何画板演示，让学生形成正弦曲线的初步的了解，理解正弦函数、余弦函数图象的作法。培养学生用数学眼光观察世界，提升数学抽象、直观想象等数学学科素养。

2.本节要掌握用“五点作图法”作图，熟练地画出一些较简单的函数图象.当学生遇到新问题时，他们知道如何利用新旧知识之间的联系，从抽象到具体，运用化归、类比、数形结合等数学思想方法来解决实际问题。

教学问题诊断

1.高一学生已具备了一定思维能力和数形结合等数学思想方法，能力发展正处于形象思维向抽象思维转折阶段，但更注重形象思维。因此，本节课通过教师演示、问题探究、学生自己動手画图等交流互动方式，加强数学直观，渗透数形结合思想，注重新知识的生成过程，引导学生一步步达成教学目标。

2.基于以上分析，确定本节课的难点是：画出正弦函数在一个周期内的图象及图象变换。

教学支持条件分析

为使课堂直观生动，易于突破难点，可用几何画板进行作图演示，加强学生对图象的直观感知，形成数形结合的思维认知，发展直观想象的核心素养。

教学过程设计

环节一：创设问题情境

在现实中，不乏一些圆周运动的事例。如坐落天津永定桥的被称为“天津之眼”的摩天轮，摩天轮上的座椅做的是圆周运动。还有中国古代灌溉用的水车，做的也是圆周运动。

师生活动设计：

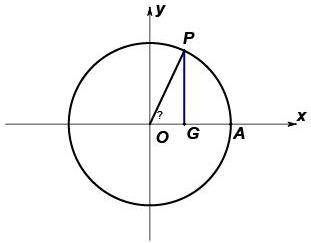
教师提出问题：用什么样的函数模型来描述圆周运动呢？待学生思考并回答后，教师追问：怎么用三角函数来描述圆周运动呢？学生思考并回答后，紧接着教师又抛出一个问题：一个质点在单位圆上的点A处，这个质点在单位圆上绕圆心以逆时针方向做圆周运动，当质点转了[α]弧度到点P，请问质点的位置如何表示？教师针对学生的回答说明：可以用三角函数来描述圆周运动，质点的位置用P（cos [α]，sin [α]）来表示，用x替代[α]，所以点P的纵坐标和横坐标可分别用正弦函数y=sin x及余弦函数y=cos x表示。所以可用三角函数来描述圆周运动。

【设计意图】通过问题引导，既复习巩固了三角函数的有关知识，为新课的教学做好铺垫，又培养和发展数学建模等核心素养。

环节二：探索新知

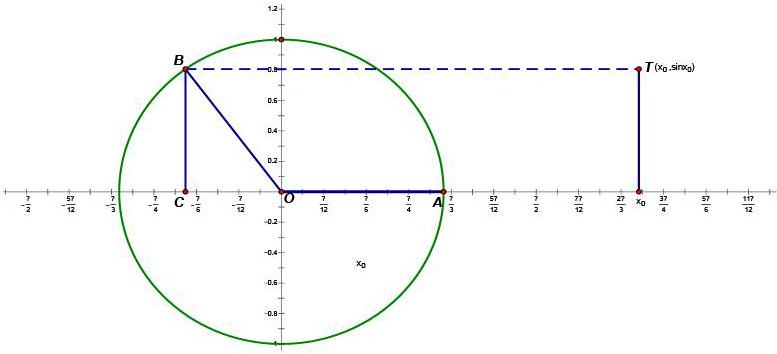
师生活动设计：怎么画出正弦函数的图象？引导学生复习指数函数的作图方法，得出可用描点法，学生取点，教师进行说明：在对正弦函数的图象还不了解的情况下，很难确定应该描出哪些点作为代表，因此，我们无论取多少点，都不能保证图形是准确的，怎么做呢？首先，我们不需要描很多点，用局部来研究整体。

【设计意图】借助三角函数定义，引出作正弦函数图象的方法，培养学生的逻辑推理、数学抽象等素养。

师生活动设计：

【设计意图】学生在教师启发式教学引导下，很自然地从点的坐标进而得到一个周期内的坐标。

师生活动设计：

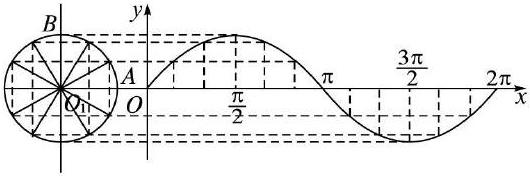
问题4：你能描述一下正弦曲线的大致形状吗？

教师可说明，如：波浪形的、向两边无限延伸的光滑曲线等。

【设计意图】体现部分与整体的关系，促进抽象到具体及数形结合思想方法的形成，提升直观想象素养。

师生活动设计：

问题5：在一个周期内的正弦函数图象也有几个最关键的点，有了这些点之后，函数图象基本会被确定下来，这几个点是什么？

【设计意图】找出画正弦函数的关键点，掌握“五点作图法”的一般步骤：列表、描点、连线。

师生活动设计：

问题6：怎么作出余弦函数的图象？

用刚学的方法，就是有点麻烦。

【设计意图】通过图象变换画出余弦函数图象，提升学生逻辑推理、直观想象等素养。

环节三：初步应用

师生活动设计：

例1画出下列函数的简图

【设计意图】学以致用，通过例题训练和发展学生的知识应用能力。

环节四：目标检测

【设计意图】通过目标检测，巩固本节所学知识，加强对本节知识的理解，提升学生的直观想象、逻辑推理等素养.

环节五：课堂小结

师生活动设计：

提出问题：

1.通过本节课的学习，你学会了如何画正弦（余弦）曲线？

2.“五点法”作图中的五点是哪五点？

3.作余弦函数的图象体现了什么思想？运用了什么方法？

【设计意图】培养学生养成反思的习惯，用数学语言进行表达和沟通，发展学生的直观想象、逻辑推理等素养。

教学设计反思：

本节课的教学设计有如下特点：

1.本节课精心设置问题情境，从中国古代灌溉用的水车和摩天轮做圆周运动说起， 进行数学建模，间接地显示了作图的方法，同时，学生也感受到数学是来源于生活，无形中受到数学文化的熏陶。

2.本节课采用从特殊到一般，从部分到整体的策略，来探索正弦函数的图象。教师利用多媒体等教学手段，使抽象问题既具体又直观，充分考虑这一学段学生的思维特点。

3.本节课精心设置多个问题，下个问题与上个问题紧密相连，使知识的形成既环环相扣，一气呵成，又贴切自然，符合学生的认知规律和习惯。

数学核心素养对人的发展有着深远的影响，所以数学教学不仅仅是知识和技能的传授，更重要的是数学思想的熏陶以及数学核心素养的养成。纵观本节课的教学设计，我们不难得到这样的启发：教学要学生为本，重视知识的生成过程，揭示知识的内在实质，这样才能真正发展学生的数学核心素养。

参考文献

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

[2]王尙志.如何在数学教育中提升学生的数学核心素养[J].中国教师，2016（9）：33-38.