集装箱码头送箱外集卡预约优化研究
2021-10-14张成成
丁 一,张成成
上海海事大学 物流研究中心,上海 201306
集装箱化提高了港口装卸效率,降低了货运成本,促进了世界贸易增长,却给集装箱码头的运营带来诸多挑战。大量集卡的集中到达和无序管理,使码头设施处于满负荷或接近满负荷的运转状态。集卡必须在码头闸口或堆场等待很长时间,导致码头严重拥堵,降低了货运系统的整体效率。因此,如何减少集卡排队长度成为提高码头运营效率的关键环节。
近年来,许多对于此问题的研究成果可以分为两类:第一类是扩大码头面积,增加闸口等基础设施。然而这类方法由于土地和资源的有限性,应用非常有限;第二类是管理集装箱码头的集卡,提高码头运营效率。建立集卡预约系统就是第二类中的典型方法。
关于集卡预约系统的研究,Chen[1]将其分为两个阶段,即静态预约系统(STAS)阶段和动态预约系统(DTAS)阶段。STAS 是码头运营商通过一个专有信息系统公布开放的预约时间窗和各时间窗的预约份额后,集卡司机选择自己到达码头的时间窗。而DTAS 是一个实时系统,其运行模式为每个集卡司机登录一个专有网站,提出预约请求,然后码头运营商基于现有预约进行评估,即如果不太可能发生长队列,则接受该请求,否则拒绝请求。被拒绝的集卡司机重新提出预约请求,直到DTAS 接受该请求并把它添加到现有预约中。近年来,大多文献都是基于DTAS 对集卡预约系统进行研究。Phan和Kim[2]提出了一种由集卡公司和码头运营商共同决定集卡运营计划和到达时间窗的预约程序,建立了包含集卡公司子问题和码头运营子问题的数学模型,来确定集卡最优调度计划和各时间窗期望的预约份额。Caballini[3]提出了码头环境下多辆集卡运输协同规划的优化模型,引入了补偿机制来激励集卡司机分享他们的实时运输。Schulte[4]提出的集卡司机协作规划模式与集卡预约系统共同应用,有效减少了集卡空载和成本。Torkjazi[5]提出了一种集卡预约系统设计新方法。一方面码头运营商尽量平均分配每日抵港集卡的数量;另一方面,该系统考虑集卡公司成本来提供预约时间窗,以减小集卡到达时间与原定时间表的差距。由此可见,DTAS模式能够根据现有预约实时的估计等待时间,可以更好地协助集卡司机预约,进而有效地减少码头拥堵的发生,实现码头运营商和集卡公司协同效益的最大化,显著提高预约系统的灵活性。
减小集卡排队长度是建立集卡预约系统的最终目的,因此需要一个精确的模型来估算集卡队列的长度。在已有研究中,平稳排队模型是研究排队系统的经典工具,它根据集装箱码头闸口系统的物理布局和特点,提出多服务器排队模型来分析集卡队列。Guan和Liu[6]就曾使用多服务器排队模型M/Ek/s 来分析纽约某集装箱码头的闸口排队情况。Kim[7]提出了基于M/G/1排队过程的非线性整数规划模型来分析收费站的车辆排队情况。然而,平稳排队模型认为集卡队列可以在瞬间达到平稳状态,忽略了集卡到达和闸口服务率随时间变化的现实状况。因此,它只适用于排队系统达到平稳状态的情况,缺乏现实意义。Smith 证明了状态相关队列可以有效反映集卡的动态排队情况,提出了非平稳排队模型。在此基础上,Chen[8]提出了逐点固定流体近似算法(PSFFA),开发了一个包含闸口和堆场的两级排队网络,并通过实例证明了该排队模型可以模拟出闸口通道和堆场分区的车辆排队情况。文献[9]基于文献[6]的研究发现集卡到达闸口的过程服从指数分布,闸口服务时间服从4阶埃尔朗分布,因此在PSFFA的基础上提出了B-PSFFA 方法。基于该方法的非平稳排队模型与文献[6]的平稳模型比较的结果表明,非平稳排队模型的准确度更高[10]。曾庆成等[11]也针对码头闸口拥堵问题,建立了预约优化模型,设计了基于遗传算法与PSFFA的求解方法。杨宇[12]研究集卡在闸口和堆场的两级排队系统,引入精英策略的自适应遗传算法求解,得到集卡最优预约份额。由此可见,建立非平稳排队模型更符合集卡到达码头随时间变化的非稳态现实,比平稳排队模型对集卡在码头的排队情况模拟的更加准确。近年来,仿真技术由于可以拟合集卡在码头的动态排队过程,也在集装箱码头的研究中得到广泛应用。Chen和Yang[13]利用PARAMIC仿真软件开发了基于仿真的回归模型,发现集卡排队的动态过程遵循自然对数曲线,进而开发了排队长度估计模型。然而与其他类型的仿真一样,集卡排队仿真是一项耗时的研究。因此,对于集卡队列长度的估算,建立非平稳排队模型是节省时间和成本,提高准确度的最佳选择。
综上所述,码头拥堵问题是港口物流运作优化的研究重点。考虑码头运营商和集卡公司双方利益,实现协同效益的最大化是当前集卡预约系统的研究趋势[14],且鉴于外集卡到达码头具有随时间变化的非稳态特征[8],建立非平稳排队模型更有意义。同时,考虑到码头内部作业系统是一个复杂的系统,堆场和闸口等作业系统相互影响,送箱外集卡将集装箱从码头外部运至堆场等待装船的过程不仅受闸口和堆场两级服务系统的影响,而且受场桥作业模式和内集卡的影响[15],本文将在考虑内集卡到达堆场模式的基础上,把外集卡必经的闸口和堆场看作两级排队系统,建立非平稳排队模型描述外集卡在闸口和堆场的排队过程,同时考虑集卡公司的利益,尽量减小集卡公司期望到达的预约时间段与被码头运营商调配到的预约时间段之间的差距[16],从而建立多目标规划模型,揭示外集卡到达规律。最后,通过CPLEX求解模型,将结果与蒙特卡罗仿真结果比较来验证模型有效性,同时调整参数优化预约模式,期望为提高码头运营效率提供参考。
1 问题描述
码头运营商通过建立集卡预约系统,设置闸口通道和堆场分区的数目以及预约时间窗。集卡公司根据自己的情况预约期望到达的时间窗,每个时间窗则根据先到先得的原则预约。码头运营商基于现有的预约进行评估,估算各个预约时间窗的预计集卡排队长度,在考虑集卡公司利益和码头拥堵状况的基础上,对各时间窗的集卡数量进行再调配,确定最终的集卡进港时间方案。
由于码头内部作业系统的复杂性,外集卡通过预约系统预约进港直到卸箱完成的过程不仅受到闸口服务系统的影响,也与码头堆场作业能力,场桥作业要求等密切相关[17]。外集卡在码头的运行流程如图1所示。

图1 集卡在码头内部运行路线Fig.1 Route of truck running at terminal
因此,本文考虑集卡公司和码头运营商双方的利益建立多目标规划模型。目标一最小化外集卡在码头的平均排队长度,考虑内集卡到达堆场模式的基础上,运用排队论相关知识和PSFFA 方法建立非平稳二级网络排队模型。目标二最小化集卡公司所期望到达的预约时间段与被调配到的预约时间段的差值,建立集卡预约优化模型,揭示外集卡到达规律,优化外集卡送箱过程,期望得到一个使集卡公司和码头运营商双赢的集卡调度计划。
2 模型构建
2.1 模型假设
为构建模型,假设:(1)闸口和堆场以先到先服务为原则服务外集卡;(2)模型忽略不计进口集装箱对堆场和闸口作业的影响;(3)模型不考虑码头设备发生故障等这一类不确定的因素;(4)成功预约的集卡均能准时到达码头;(5)场桥优先服务内集卡。当堆场有内集卡等待时,场桥无论是否处于休假模式都立即为内集卡服务。因此,外集卡的额外等待时间即为场桥为内集卡服务的总时长。
2.2 模型符号说明
为构建模型,定义模型符号见表1。

表1 模型符号定义Table 1 Definition of model’s notation
2.3 模型建立
根据排队论知识和PSFFA方法(PSFFA方法示意图见图2),多目标预约优化模型可以表示为:

图2 PSFFA方法示意图Fig.2 Diagram of PSFFA

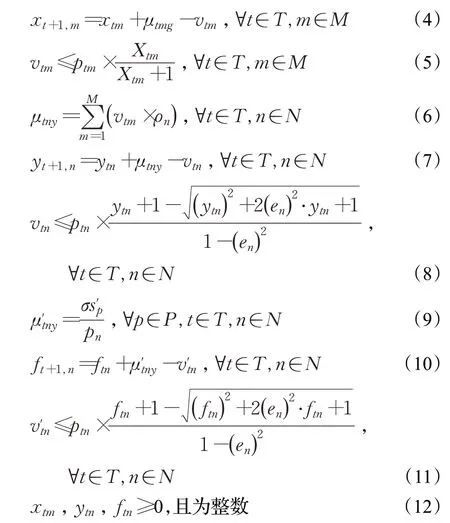
式(1)保证集卡在各时间窗的预约数量和实际到达量相等;式(2)保证调配前后集卡总数量相等;式(3)为各时段各闸口通道外集卡到达量计算公式;式(4)和(5)表示外集卡在闸口通道的排队过程,其中式(5)是根据排队论中M/M/1 排队模型的相关定理得出的集卡在闸口的出度约束;式(6)表示到达堆场分区的外集卡流量;式(7)和(8)表示外集卡在堆场分区的排队过程,其中,式(8)是根据相关研究和排队论中M/G/1排队模型的相关定理得出的集卡在堆场的出度约束;式(9)为各时段各堆场分区内集卡到达量的计算公式;式(10)和(11)表示内集卡在堆场的排队过程;式(12)为非负约束。
2.4 总周转时间计算
为了更好地控制预约系统,有必要量化外集卡在码头的总周转时间。本文假设外集卡在码头的总周转时间只包括在闸口和堆场的停留时间,忽略不计其他干扰因素。此计算沿用上述模型假设和符号。设总周转时间为W:
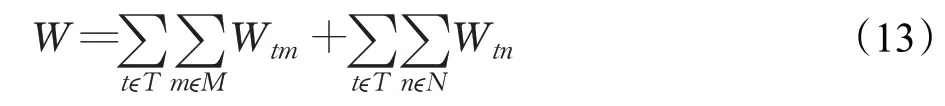
根据外集卡在闸口和堆场的到达量和离开率,可求出其在码头的总周转时间。
外集卡到达闸口的总量(假设外集卡在t时刻到达闸口):

同理,外集卡离开堆场分区的总量(假设外集卡在t′时刻离开堆场):

因此,在先进先出条件下,外集卡在码头的总周转时间可表示为:

其中D-1(t′)为D(t′)的反函数。通过上述公式,就能算出集卡在码头的总周转时间,从而为外集卡选择更合适的预约时段提供更直观的反映。
3 实例分析
3.1 模型检验
本节根据上海外高桥某码头9 月份某天的数据来验证上述数学模型,该模型场景包含4 个闸口通道和3个堆场分区,并且每个集卡可装载两个标准TEU 集装箱。本文设置分析时间为16个小时(6:00到22:00),预约时间窗为1小时,共有16个时间窗。外集卡从闸口分配到各堆场分区的比例相同。表2 列明了本次算例的内外集卡数量参数。

表2 上海外高桥码头某天各时段集卡数量Table 2 Quantity of trucks at Shanghai Waigaoqiao terminal
算例中内外集卡各时段到达闸口和堆场的过程服从泊松分布,各闸口通道和堆场分区的服务时间分别服从指数分布和正态分布。集卡在闸口通道和堆场分区的平均服务时间分别为2 min 和5 min。本节基于PSFFA方法,使用CPLEX12.6 求解,并与使用蒙特卡罗方法(Monte Carlo method)的仿真实验的结果进行比较。蒙特·卡罗仿真算法在Matlab中求解。为了保证仿真实验结果的准确性,本文对该场景进行1 500 次模拟仿真。CPLEX求解和蒙特卡罗仿真结果的对比见图3和图4。

图3 外集卡在各闸口通道的平均排队长度对比Fig.3 Comparison of average number of external trucks at gate lanes

图4 外集卡在各堆场分区的平均排队长度对比Fig.4 Comparison of average number of external trucks at yards
图3 和图4 比较了预约前后CPLEX 求解和蒙特卡罗仿真估算的外集卡在闸口通道和堆场分区的集卡平均排队数量。实验结果首先表明,基于PSFFA方法建立模型并使用CPLEX求解的结果与蒙特卡罗仿真估算的结果具有一致性。图3 中(a)图和(b)图的平均绝对误差分别为0.041 和0.032,图4 中(a)图和(b)图的平均绝对误差分别为0.124和0.976,误差较小。该结果证明了CPLEX 求解的有效性。然后,实验结果也表明了建立集卡预约系统是非常有必要的。码头运营商通过集卡预约系统对预约的集卡进行调节,减缓了高峰时期的集卡拥堵,减少了排队时间。图中所示的场景包含了泊松到达过程和正态分布的堆场服务时间,是典型的M/G/1系统,验证了本文的优化模型对更一般的服务时间分布的适用性。此模型也对闸口和堆场的平均排队长度给出了合理的预测。通过此模型计算得出,建立预约系统前闸口处的平均排队长度约为1.817,堆场的平均排队长度约为9.842,与码头实际排队长度误差较小,验证了模型的有效性。建立预约系统之后,闸口处的平均排队长度减少至1.436,堆场处的平均排队长度减少至7.673,证明了建立集卡预约系统的必要性。
3.2 参数变化影响
本文在校验了模型准确性的基础上,探究了部分参数的变化对优化结果的影响。
首先,时间间隔t的区间长度是影响此优化问题的重要参数。图5和图6绘制了不同t下闸口通道和堆场分区的集卡平均数量随时间变化的对比图。由图可得,随着t的增大,集卡平均排队数量随时间变化的反应速度降低。尤其是t取30 min时,集卡平均排队数量并不能随时间的变化做出快速反应。
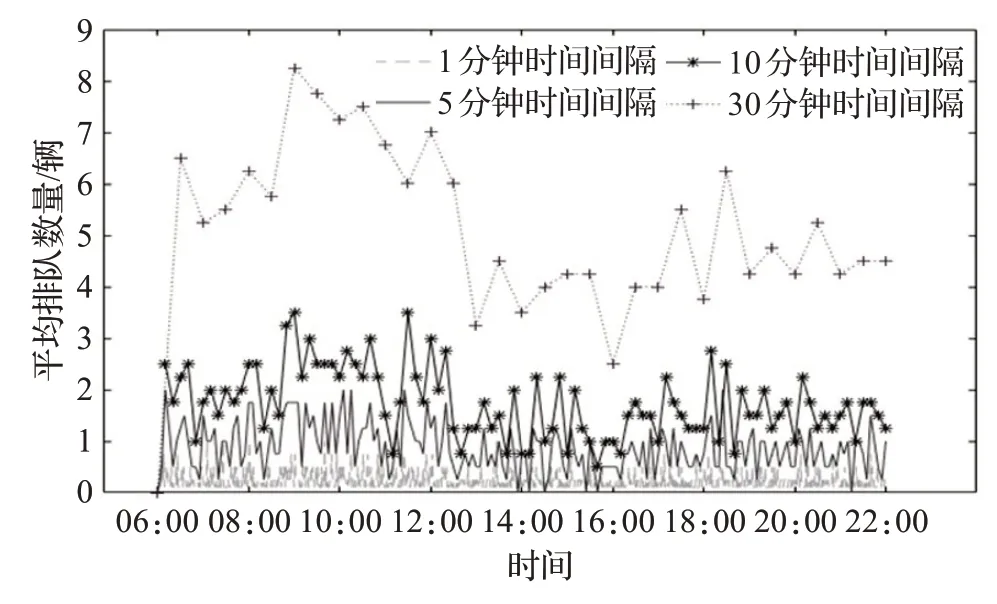
图5 闸口通道外集卡的平均排队数量变化对比Fig.5 Comparison of average number of external truck at gate lanes

图6 堆场分区集卡的平均排队数量变化对比Fig.6 Comparison of average number of external truck at yards
闸口和堆场的最大服务能力和利用率是影响集卡预约调整量的重要因素。堆场子系统往往是码头系统的瓶颈,所以本文分析了堆场在不同利用率下各预约时间段的集卡调整量。图7和图8分别是低水平和高水平堆场利用率下集卡由期望到达时间窗被调配到其他时间窗的数量分布图。由图可知,低水平利用率下,集卡调配量小,多数集卡司机能成功预约自己期望到达的时间窗;而高水平利用率下,许多集卡在高峰时期要接受调配,以减少码头拥堵。
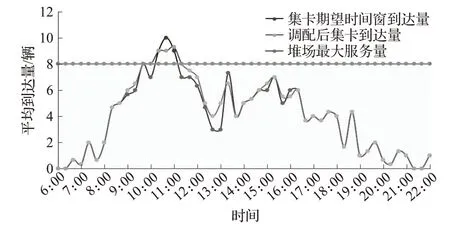
图7 低水平堆场利用率下被调配的集卡数量分布Fig.7 Quantity of assigned trucks under low utilization of yard

图8 高水平堆场利用率下被调配的集卡数量分布Fig.8 Quantity of assigned trucks under high utilization of yard
最后,在此基础上根据2.4 节中总周转时间的计算公式,得到不同时间间隔下码头运营商对外集卡的调配量以及外集卡在码头的平均周转时间的变化,见表3。实验结果表明,随着时间间隔t的增大,集卡的平均周转时间增加。但是,预约的时间间隔越短,无法按时到达码头的集卡数量越多,被调配的集卡总量就越多。因此,码头运营商应在保证平均周转时间不超过一定水平的前提下,适度增加预约时间窗长度,以提高集卡到达码头的准时率。

表3 集卡调配量和平均周转时间变化Table 3 Changes of assigned number and average turn time of trucks
4 结束语
本文考虑集卡公司和码头运营商双方的利益以及码头内部作业系统的复杂性,以减小外集卡在预约时间窗内的平均排队长度和减小集卡公司期望到达的时间窗与被调配到的时间窗间的差异为目标,运用排队论和PSFFA 方法,建立了多目标规划模型。进而,本文引入实例数据,通过CPLEX求解模型,并将结果与蒙特卡罗仿真结果比较,验证了模型有效性。此外,本文还分析了参数变化对预约模式的影响,得出以下结论:
(1)时间间隔t的区间长度是影响集装箱码头外集卡排队长度优化问题的一个重要参数。随着时间间隔t的增大,集卡平均排队数量随时间变化的反应速度降低,尤其是当时间间隔t取30 min 时,集卡平均排队数量并不能随着时间的变化而做出快速的反应。
(2)闸口和堆场的最大服务量和利用率是影响集卡预约调整量的重要因素。在低水平的利用率下,集卡的调配量小,大多数的集卡司机可以成功预约到自己期望的到达时间窗。而在高水平的利用率下,许多集卡在高峰时期要接受码头运营商的调配,以减少码头拥堵。
(3)通过计算外集卡在码头的平均周转时间得出,随着时间间隔t的增大,集卡的平均周转时间增加。但预约的时间间隔越短,无法按时到达的集卡数量越多,集卡被调配的总量增加,进而损害了集卡公司的利益。因此,码头运营商应在保证平均周转时间不超过一定水平的前提下,增加预约时间窗长度,提高集卡到达码头的准时率。
本文提出的多目标规划模型能准确描述集卡在闸口和堆场的排队情况,有效管理和控制集卡到达模式,进而确定了一个使集卡公司和码头运营商双赢的最优集卡调度计划,最大化了集卡公司和码头运营商的协同效益。
