高精度质心测量系统设计与分析

李楠,骆旭,王丽,赵静

(航空工业北京长城计量测试技术研究所,北京100095)

0 引言

质心是物体质量中心的简称,指物质系统上被认为质量集中于此的一个假想点。质心位置参数直接影响着精准打击、机动性能和姿态控制等武器装备的核心问题。其测量分析是武器装备设计、研制、试验、生产的重要内容[1-2]。

目前国内外主流的质心测量方法有多点称重法和不平衡力矩法[3]。

多点称重法是国内最常见的测量方法。质心测量设备一般是用3个或者多个传感器共同支承测量台。通过传感器相对测量台中心求矩计算质心位置,这种方法主要依赖于标校体标定出传感器坐标位置,但标校体的质心位置是假设其材料密度绝对均匀的理论值,质心位置对材料均匀性的依赖性大,且准确度无法再向上溯源[4-5]。

不平衡力矩法测量设备的内部有一个枢轴,枢轴与测量台有一个连接点,若被测件质心相对于连接点存在一定偏移,则会对平台产生一个不平衡力矩,其值为质心偏矩力臂长度与被测件所受重力的乘积。被测件所受重力易于获得,且可通过力矩传感器获得不平衡力矩,进而换算出质心偏矩。美国Space Electronics公司(现为Raptor Scientific)研发的SE系列和KSR系列均以此为基础进行制造,主要适用于航空航天领域对高精度质心参数测量有需求的回转体[6-7]。

目前各武器装备中生产研制单位质心测量仪众多,在使用中缺少科学的校准方法,同时缺少更高准确的校准装置。

本文介绍了一种基于质量反应法的高精度二维质心测量装置。该装置脱胎于机械天平,利用杠杆平衡原理获得样件坐标位置。在原有一维机械天平的基础上通过拓宽横梁、增加X轴、Y轴支撑机构和测量机构等方式对原机械结构进行改进,形成了二维的杠杆平衡机械结构。装置的负载范围为100～3000 kg,可对长度不大于1.5 m、直径不大于0.6 m的被测样件进行高精度测量。

1 测量原理

高精度质心测量系统主要以杠杆原理为基础的机械天平进行设计,杠杆原理如图1所示。

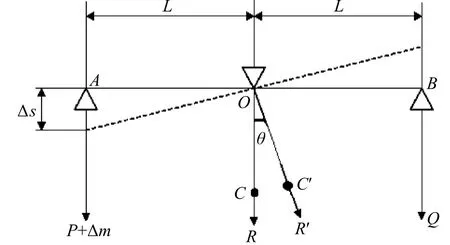
图1 杠杆原理图

横梁上的三处支撑结构处于同一水平面,设臂长OA=OB=L,两吊挂系统的质量分别为P和Q,且P=Q。横梁自重为R,质心位于点C,OC=hc,当机械部分处于平衡状态时,则PL=QL。若增加质量为Δm,则横梁偏转θ角,点C偏至点C′,此时力矩方程为

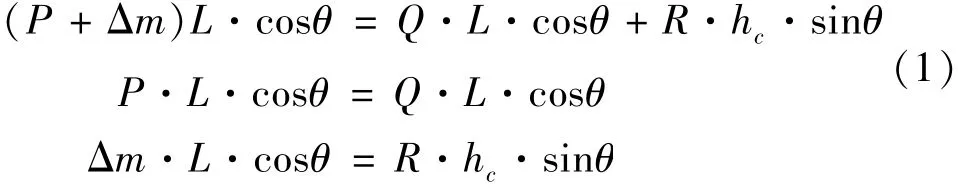
当θ=0时,cosθ=1;sinθ=Δs/L

则Δm·L=R·hc·Δs/L

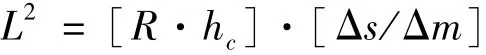
式中:[R·hc]为机械恢复力矩系数;[Δs/Δm]为灵敏度;[R·hc]为正比于稳定性。

高精度质心测量系统由杠杆平衡测量系统和电磁力自动测量系统构成,测量原理如图2所示。

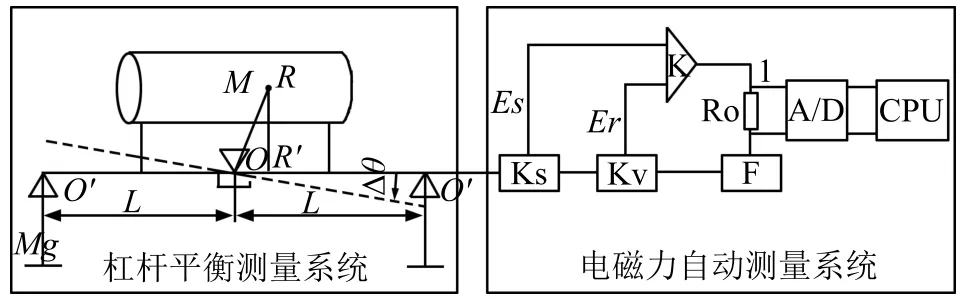
图2 质心测量原理示意图

杠杆平衡测量系统中,O为支点;R为被测样件质心;R′为质心在水平方向的投影;M为被测样件质量;L为系统平衡盘力臂长;m为平衡质量。测量时,被测样件直接加载在横梁上,通过O点(支点刀)支撑,以O点为旋转中心,此时被测样件质心位置在R点,形成力矩OR′,被测样件质量为M,质心偏移形成的偏心矩为Mg·OR′。

电磁力自动测量系统中,Ks为位移传感器;Kv为速度传感器;K为运算放大器;R0为采样电阻;F为力矩器。称量时通过电磁补偿力矩的作用而达到杠杆平衡。Es为位移误差,Er为速度误差,通过计算得到被测样件质心位置OR′。

当被测样件加载在横梁上时,偏心所形成的力矩会使横梁向一方倾斜,位移传感器Ks测量出转角Δθ,然后位移传感器将位移信号变成电信号,经位移放大器放大,再经运算放大器K的放大,负反馈给力矩器F以电流使力矩器产生力矩(即电磁恢复力矩),从而使横梁向反向倾斜,最终使得电磁力矩与偏心力矩平衡。此时电磁力矩与质心偏心所产生的不平衡力矩大小相等方向、相反,形成一一对应关系,由于电磁力矩与力矩器F中的电流为唯一对应关系,在被测样件质量不变的情况下,其质心相对于支点O的水平位置OR′与力矩器中的电流I形成唯一对应关系。电流通过采样电阻R0,便可通过A/D转换成所需的数字信号。

2 系统结构与测量方法

高精度质心测量系统在精密电磁天平原有的一维杠杆基础上对横梁进行拓宽,形成具有两套正交支点刀支撑机构的二维杠杆平衡结构,如图3所示。为了提高系统的稳定性并保证测量精度,系统在X方向和Y方向分别设有支撑机构实现x轴和y轴的质心测量。

图3 二维质心测量系统结构图

假设样件质心位置在仪器坐标系下X轴方向的位置为Δx,在Y轴方向的位置为Δy,则根据力矩平衡原理Δx,Δy可分别由公式(2)和公式(3)得到。

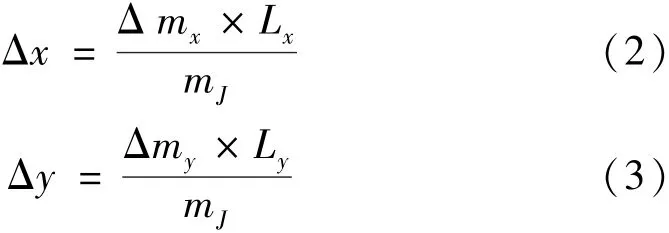
式中:Δmx为二维质心测量系统测得的由样件质心与中刀位置在X轴方向不重合而引起的质量变化量;Δmy为二维质心测量系统测得的由样件质心与中刀位置在X轴方向不重合而引起的质量变化量;Lx为二维质心测量系统X轴臂长;Ly为二维质心测量系统Y轴臂长;mJ为标准样件质量值。

通过坐标转换系统将样件轴向质心位置由仪器坐标系下转换到样件坐标系下坐标值,如图4所示。首先确定仪器坐标系和样件坐标系的相对位置,以二维质心测量系统X向边刀位置为基准点,设X1为样件坐标系原点与二维质心测量系统基准点距离,则

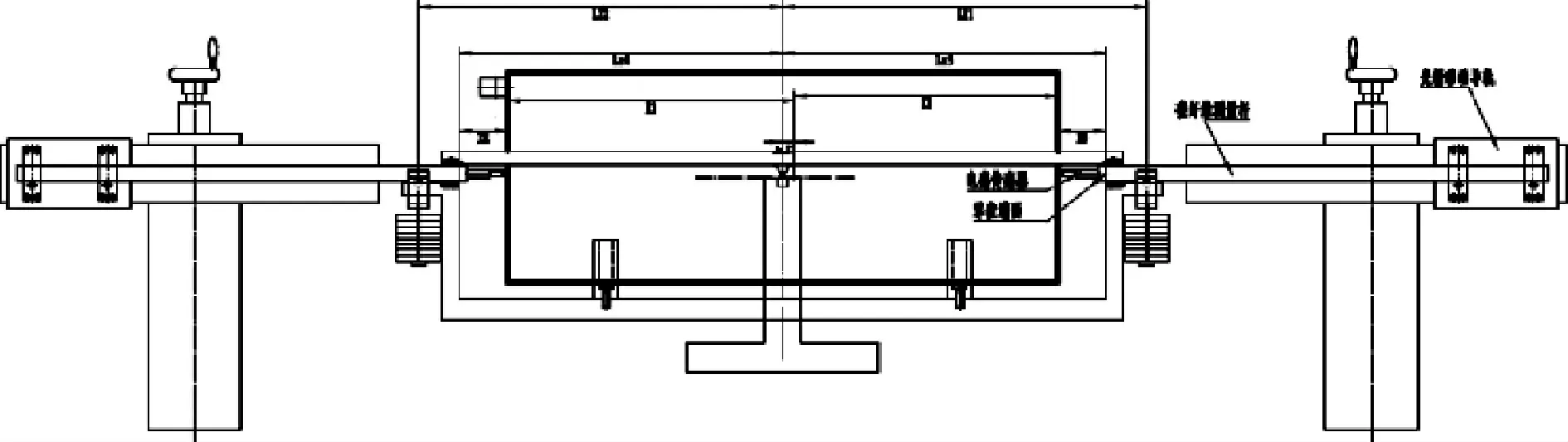
图4 坐标转换示意图

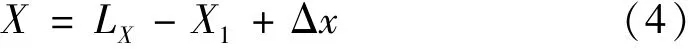
式中:X为样件坐标系下质心轴向坐标位置。

进行径向坐标转换时,其坐标系原点所在X轴线(支点刀位置)与仪器坐标系X轴可能呈平行(不重合)关系。此时装夹误差影响如下:假设样件径向坐标与其坐标原点位置重合,如图5所示,记录此时径向质心位置为y0,按图示旋转方向旋转α度后径向质心位置记为y+,返回到初始0度位置,按图示旋转方向反转α度后测量径向质心记为y-,设在初始0度位置时轴向质心的极坐标表示为(ρ,θ),则有

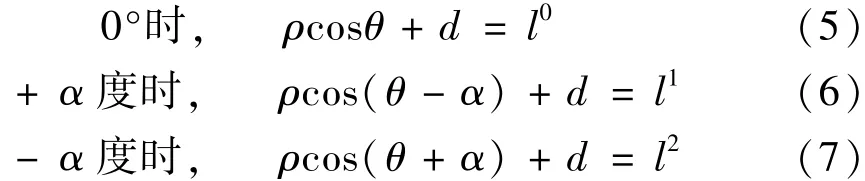
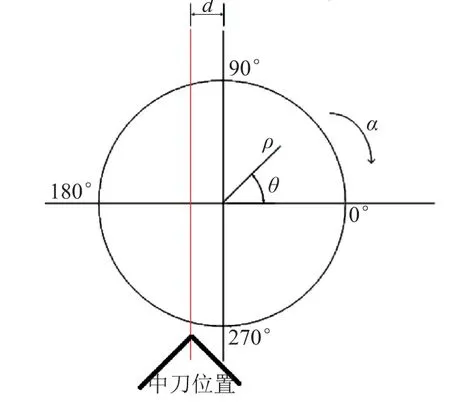
图5 样件装夹误差示意图

通过改进测量方法,可以消除装夹误差的影响。将样件置于质心测量系统上,如图6所示,其中,a为样件坐标系下径向质心位置,d为样件坐标系原点相对于支点刀所在平面的距离(装夹误差)。将样件置于0°位置时测量可得Δy0=-a-d,将样件旋转180°后再次测量可得Δy180=a-d。

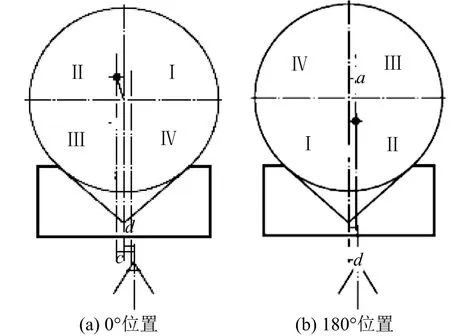
图6 样件0°位置和180°位置测量示意图

由上述测量可得

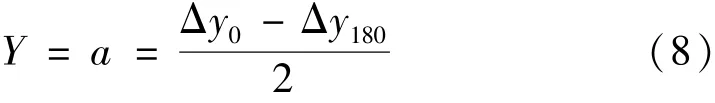
同理可得在样件坐标系下质心位置的Z坐标。

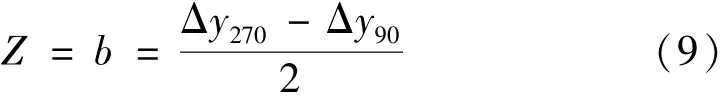
3 实验结果

利用高精度质心测量系统(如图7)对质量991.09 kg、总长1300.04 mm的质心样件进行测量。

图7 高精度质心测量系统

系统X轴臂长Lx为999.95 mm,Y轴臂长Ly为500.06 mm,均溯源至激光跟踪仪。通过系统配备的坐标转换设备,可得样件坐标系原点与二维质心测量系统基准点距离X1为351.34 mm。经测量得样件在其自身坐标系下的质心坐标为(650.47 mm,0.00 mm,0.04 mm)。对该试验结果进行不确定度分析,其数学模型分别如式(4)和式(8)所示。以轴向质心测量时,Lx,X1,Δx三者之间均不相关,相关系数视为0,由可得

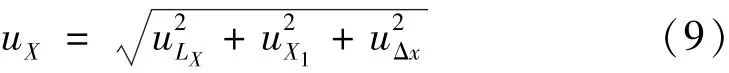
各分量引入的不确定度如表1所示[8-10]。

表1 质心样件测量结果不确定度合成

取k=2,此测量结构的轴向质心测量结果可以表示为X=650.47 mm±0.05 mm。

同理可得径向质心测量结果的扩展不确定度为0.02 mm;径向质心的测量结果可表示为Y=0.00 mm±0.02 mm;Z=0.04 mm±0.02 mm。

4 质心测量系统溯源方法

利用本文所提出的高精度质心测量系统,可建立如图8所示质心量值溯源系统。

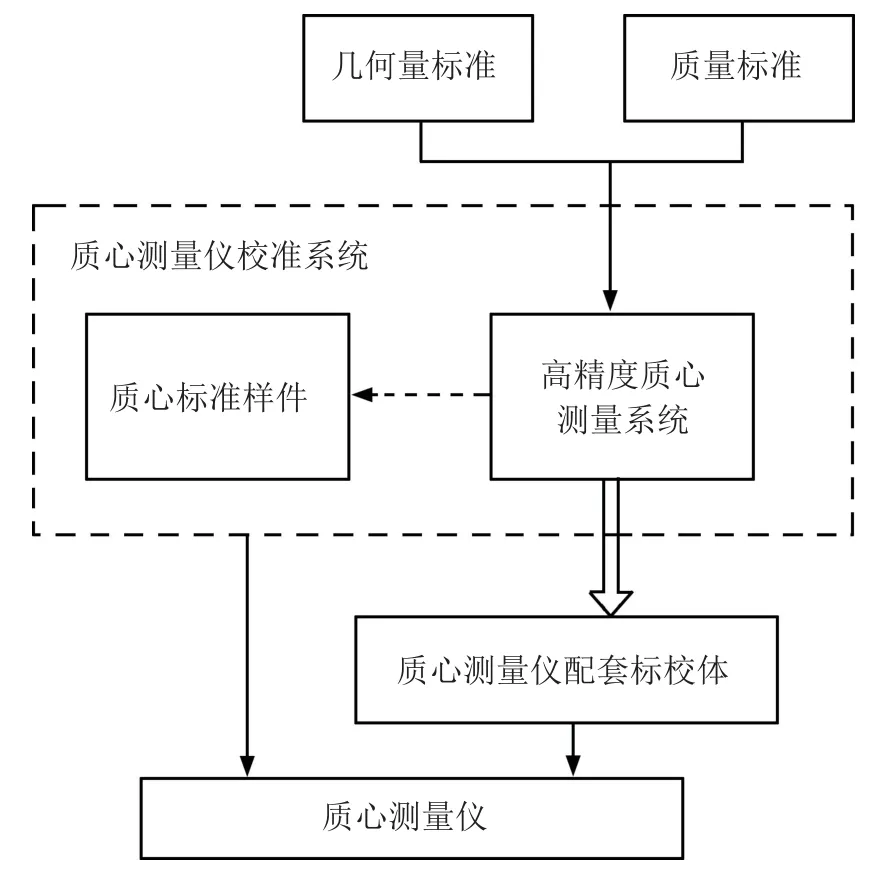
图8 质心量值溯源系统

其中,高精度质心测量系统分别溯源至几何量标准和质量标准;质心标准样件作为传递标准与其一同构成质心测量仪校准系统,用于保存质心标准量值并对质心测量仪进行校准;对于配备标校体的质心测量仪可直接将标校体溯源至高精度质心测量系统。

本文所提出的高精度质心测量系统,其臂长可溯源至激光跟踪仪或三坐标测量机;质偏引起的测量平台质量变化量相当于机械天平的不等臂误差,溯源至砝码。

5 结论

高精度质心测量系统可测量质量范围100～3000 kg的回转体质心样件,与基于多点支撑法的质心测量系统相比,克服了其称重传感器位置定位不准确的缺点,减小了测量不确定度[11];与基于不平衡力矩法的质心测量系统相比,克服了倾覆力矩的限制,提高了系统安全性,降低了系统对于进口高精度力矩传感器的依赖[12]。该测量系统在安全性、可靠性和测量准确性方面都达到了较高水平。该系统的溯源性明确,可进一步与标准样件一起构成质心测量仪校准系统,解决武器装备生产研制部门质心测量仪的溯源问题[13-14]。