多目视觉测量系统的光束法平差改进
2021-10-14别梓钒张瑞李维诗
别梓钒,张瑞,李维诗
(合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230041)
0 引言
在航空航天、汽车制造等领域,为了高速、方便、非接触地对大尺寸曲面工件进行三维测量,三维扫描测量机器人[1]逐渐得到应用。传统的三维扫描测量机器人的工作原理是:三维激光扫描测头固定在工业机器人关节臂末端,工业机器人按照规划路径运动,带动激光扫描测头扫描工件获取点云数据。由于机器人存在装配误差、惯性滞后,机器人末端的定位精度会受到限制,影响测量精度。采用多目视觉测量系统对三维扫描测头进行动态测量[2]可以消除机器人末端定位精度的影响。
摄影测量中基于共线方程的三维重建易受噪声影响,通常采用光束法平差(Bundle Adjustment,BA)对相机参数和三维坐标初值进行整体的非线性优化,以获得更精确的测量结果[3]。传统光束法平差本质上是求解非线性最小二乘问题,一般以被测点在像平面上的重投影误差作为误差函数,再以一定的最优化准则修正相关参数。许多学者对光束法平差在坐标测量领域内的应用进行了研究与改进,周维虎等人[4]运用光束法平差对激光跟踪仪的精度进行了评定,证明了光束法平差对激光跟踪仪的精度评定正确可行。郭迎钢等人[5]在激光跟踪仪光束法平差中引入马氏距离,建立起抗差马氏光束法平差模型,提升了处理精度。赵帅华等人[6]提出了BFGS-GN法,提升了光束法平差对不同类型初值的鲁棒性。徐振亮等人[7]采用轴角法代替欧拉角来描述相机的空间位姿,减少了光束法平差在迭代过程中的计算量,提升了运算效率。
在本文搭建的多目视觉系统中,由于相机与标志点之间的距离变化较大,标志点测量结果在空间中的定位误差难以评价,以二维像平面上的重投影误差作为误差函数来表征三维空间点的定位精度并不恰当;另一方面,受标定精度和镜头畸变的影响,在迭代计算过程中,光束法平差的修正主要体现在相机外参数,迭代步长在三维坐标上的修正不明显。
为解决上述问题,本文在传统光束法平差的误差方程中引入摄影比例尺,将标志点在二维图像平面上的重投影误差映射至三维空间,建立新的误差方程和目标函数,并将参数的优化分为两步,先修正经标定算法得到的相机内、外参数,再以优化后的内、外参数作为真值,迭代计算三维坐标,加强三维坐标值的修正。最后利用本文搭建的多目视觉测量系统进行实验,验证改进后的光束法平差的精度。
1 多目视觉测量系统介绍
本文搭建的多目视觉测量系统的示意图如图1所示,该系统主要由视觉传感器、专用图像处理系统[8]和计算机三部分组成。视觉传感器由4个CMOS相机组成(编号分别为1,2,3,4),以1号相机的相机坐标系作为整体测量环境的世界坐标系,4台相机采用交向摄影方式环绕布置在测量现场上方,获取扫描测头上的标志点图像,作为整个系统的信息输入来源;专用图像处理系统采用基于FPGA开发的硬件系统,用于实时、高速地进行图像处理,提高视觉系统的整体处理效率;计算机作为上位机控制视觉传感器、专用图像处理器,接收数据后进行三维重建,并输出、显示最后的计算结果。
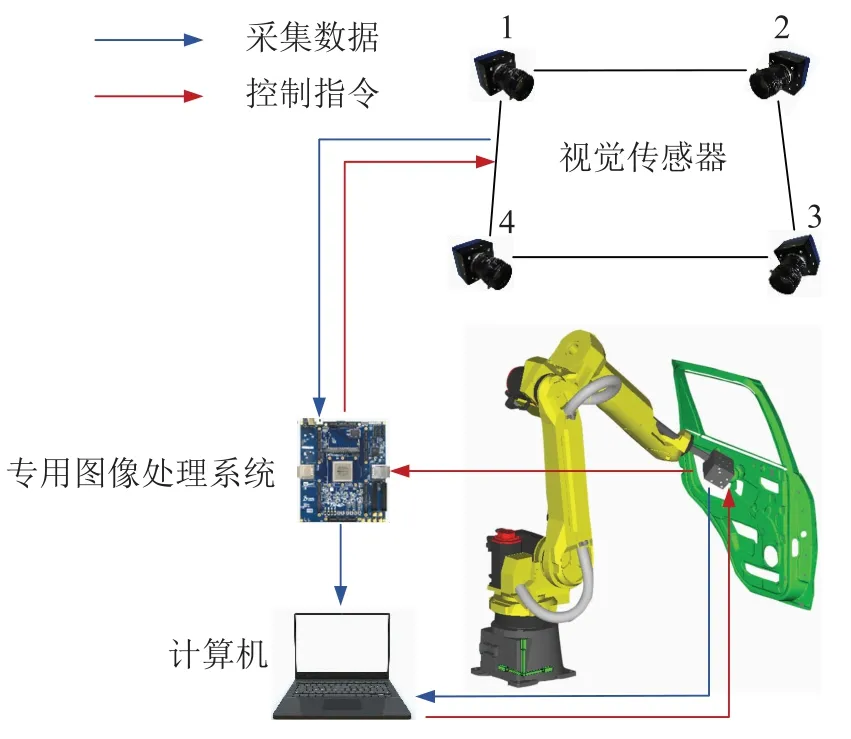
图1 多目视觉跟踪系统
2 多目视觉测量系统光束法平差
2.1 系统三维重建原理
本系统利用四台相机对扫描测头四周的编码标志点进行同步测量,通过光束法平差对系列参数进行非线性优化,得到标志点的三维坐标值。三维坐标初值计算基于共线方程,本系统的共线方程为
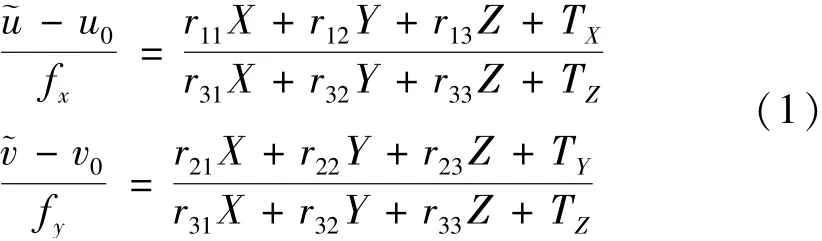
光束法平差以被测点的重投影误差作为误差方程,定义如下
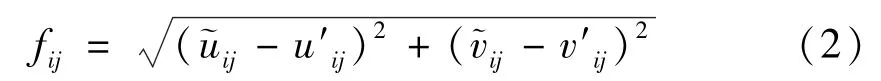
式中:fij为第i个标志点在第j个相机像平面上的重投影误差,像素;为第i个标志点在第j个相机内的像素坐标值,像素;(u′ij,v′ij)为第i个标志点在第j个相机像平面上的重投影点像素坐标值,像素。
2.2 光束法平差改进
由于相机成像时物点距离相机光心的物距远大于相机主距,每条成像光线在像平面上的微小偏差会通过摄影比例尺[9]明显放大,测量时易造成空间定位误差,如图2所示。摄影比例尺m定义如下
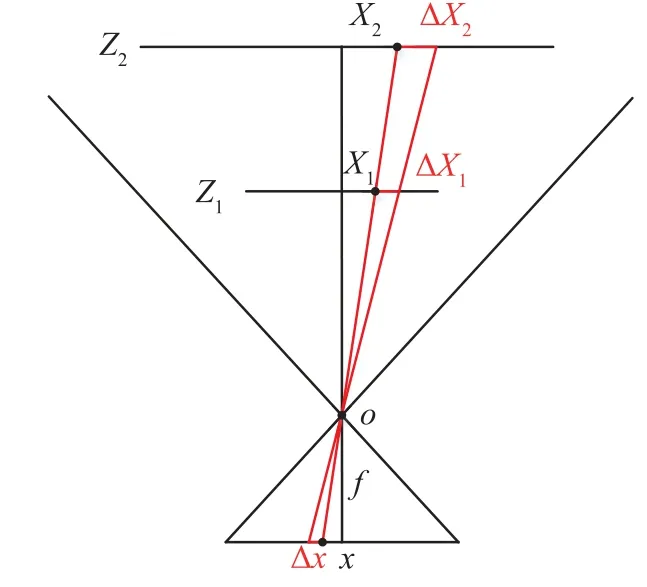
图2 摄影比例尺

式中:Z为物点和相机光心在光轴方向上的直线距离,mm;f为相机主距,mm。
在实际应用中,扫描测头处于不断运动的状态,相机与标志点之间的距离变化较大,不同成像系统的摄影比例尺也不同。当标志点与各相机之间的距离相差过大时,根据式(3),成像平面上相同大小的重投影误差所对应的空间定位误差也会明显不同。此时,不同成像系统的重投影误差对空间定位误差的评价无法统一在相同尺度上。常规光束法平差以成像平面的重投影误差作为误差方程,不适用于相机与标志点距离变化较大时的三维重建。
为将各成像系统的空间定位误差统一在同一尺度下,本文在光束法平差的误差方程基础上引入摄影比例尺,以空间定位误差作为新的误差方程。由于重投影误差以像素为单位,空间定位误差以mm为单位,将相机在像平面x,y轴方向上的主距(fx,fy)代入式(3),得到本系统的摄影比例尺mx,my,即

将式(4)中的摄影比例尺代入式(2)中,得到改进后光束法平差的误差方程为
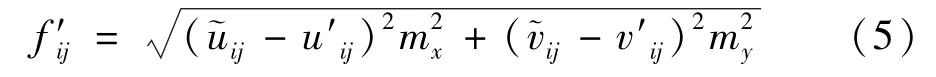
式中:f′ij为空间定位误差,表示第i个物点在空间中与第j个图像平面的成像光线之间的距离,mm。
在光束法平差的计算中,参与平差的初值受镜头畸变和相机标定精度的影响较大,因此迭代步长的修正更多地体现在相机参数上,为加强光束法平差对三维坐标的优化,本文在式(5)的基础上,将参与光束法平差的平差参数分为两部分,分步进行优化平差,即
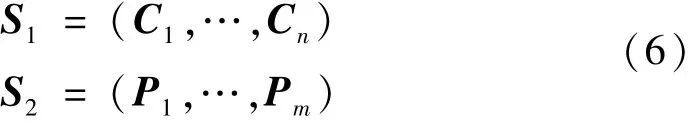
式中:S1为第一步平差的参数向量;S2为第二步平差的参数向量;n为参与重建的相机数量;m为参与重建的标志点数量;C1~C n为各相机的参数向量;P1~P m为各标志点的三维坐标向量。
利用LM算法对平差参数进行非线性优化,迭代计算的目标函数定义如下
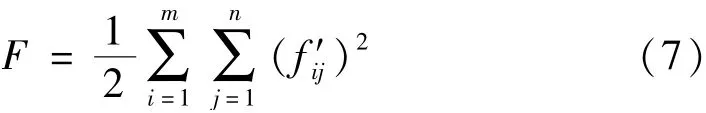
式中:F为参与重建的所有标志点的总空间定位误差,mm;m为参与重建的标志点数量;n为参与重建的相机数量。
根据式(7),在第一步平差过程中,迭代计算获得高精度的相机参数;在第二步平差过程中,将修正后的相机参数作为真值,迭代计算标志点三维坐标,最终完成对标志点的三维坐标求解。
3 实验与结果分析
为了验证改进后光束法平差对空间坐标的处理精度,本文利用多目视觉跟踪系统对Creaform公司C-Track光学动态跟踪系统的一维基准尺(如图3)进行测量。一维基准尺上粘贴有反光标志点,标志点中心之间的直线距离经过高精度标定得到。该标定尺寸作为本文实验的参考值,参考值及标准不确定度如表1所示。
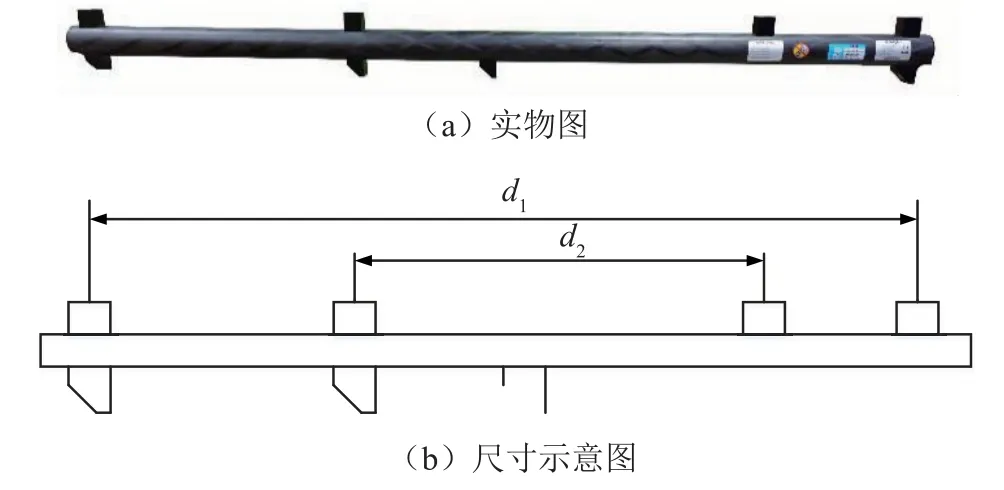
图3 C-Track系统一维基准尺

表1 C-Track系统一维基准尺数据 mm
本系统中4台相机的公共视场范围较小,且标志点大小在相机采集图像中所占比例极小,在保证标志点被准确提取的前提下,相机在沿光轴方向上的有效测量距离为1.5~2.5 m。在相机的公共视场以及相机的有效测量距离内,将一维基准尺以不同姿态在水平、纵深方向上的不同位置进行摆放,采集标志点图像。
本系统中相机内、外参数初值由张正友标定法对相机进行标定获得,标志点三维坐标初值由空间前方交会法计算获得。在剔除标志点未被识别等无效图像组后,经过三维重建和平差优化后,获得三组对d1和d2的测量数据,每组50个测量值,计算得到每组的算术平均值及算术平均值标准差。表2为重建初值的数据处理结果,表3和表4为经常规光束法平差和改进后光束法平差优化后的数据处理结果。
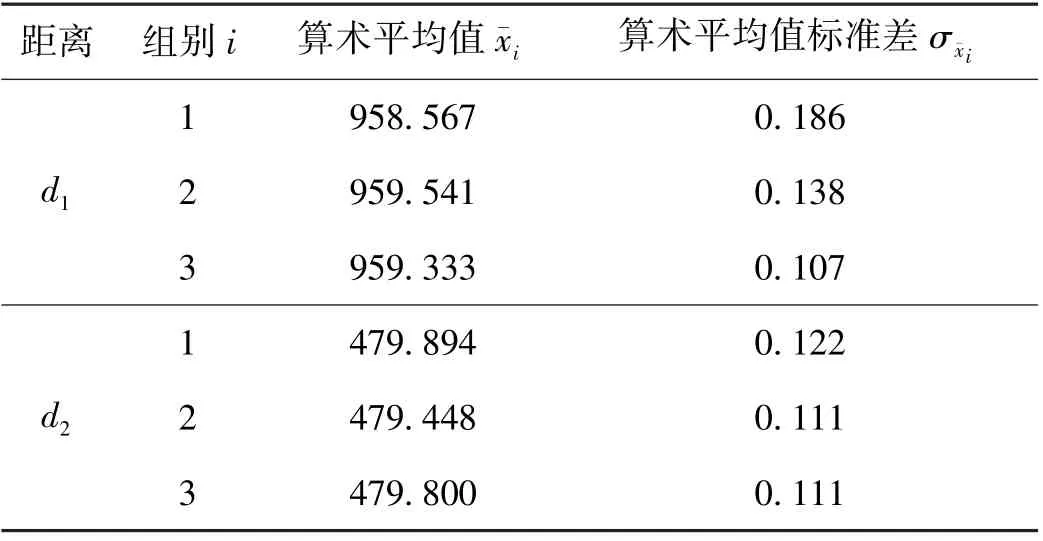
表2 重建初值数据处理结果 mm
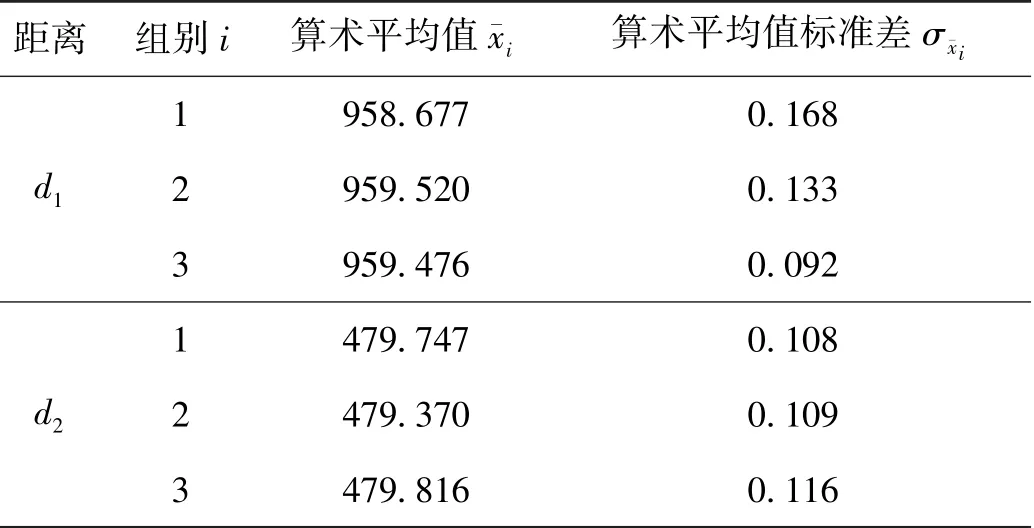
表3 光束法平差数据处理结果 mm
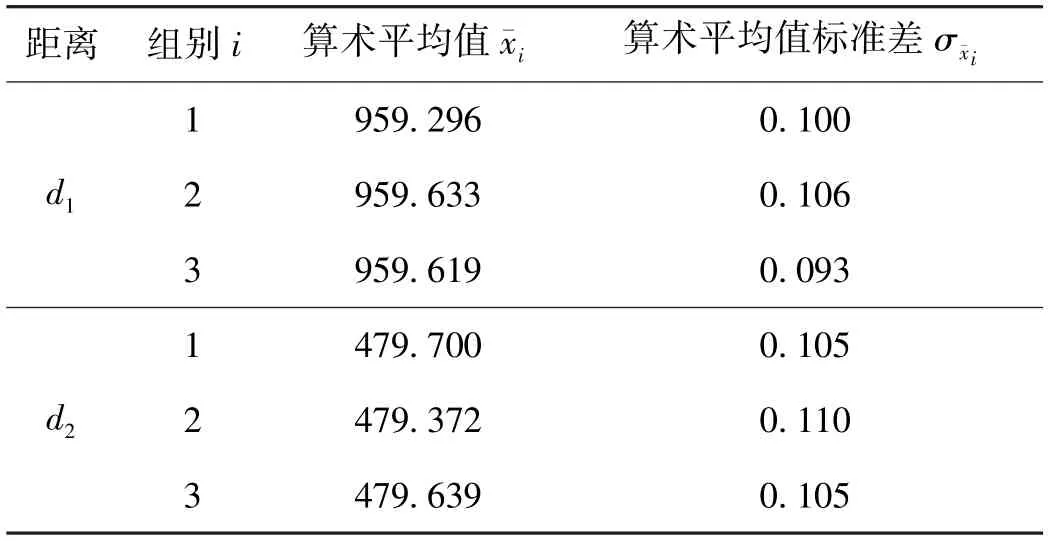
表4 改进光束法平差数据处理结果 mm
根据表2~表4中的数据可知,在测量距离d2时,重建初值、光束法平差和改进光束法平差的σ¯xi较为接近,但在测量距离d1时,重建初值的σ¯xi整体大于光束法平差的σ¯xi,光束法平差的σ¯xi整体大于改进后光束法平差的σ¯xi。这是因为距离d1较长,在摆放基准尺时,标志点更靠近相机的视场边缘,受镜头畸变影响较大,而距离d2较短,所采集图像中d2的标志点受畸变影响相较d1更小,具有更好的迭代初值。
根据表2~表4中的算术平均值,计算得出d1,d2在3组测量列中的加权算术平均值、参考值偏差及算术平均值标准差,如表5和表6所示。
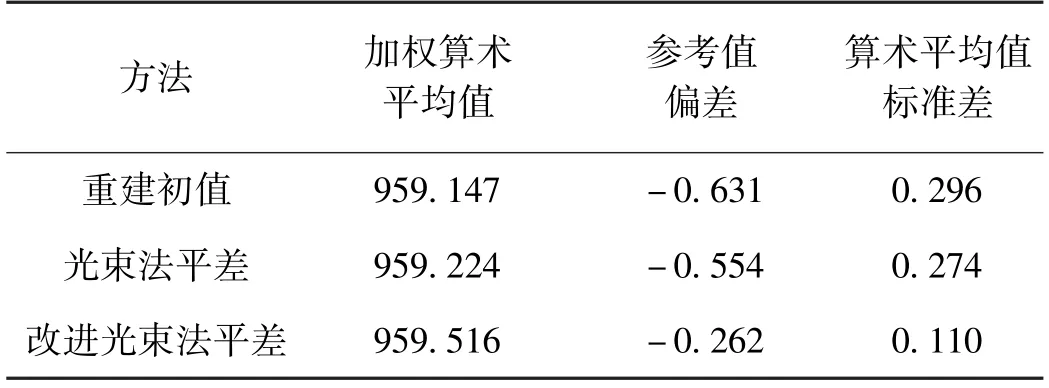
表5 d1数据处理结果 mm
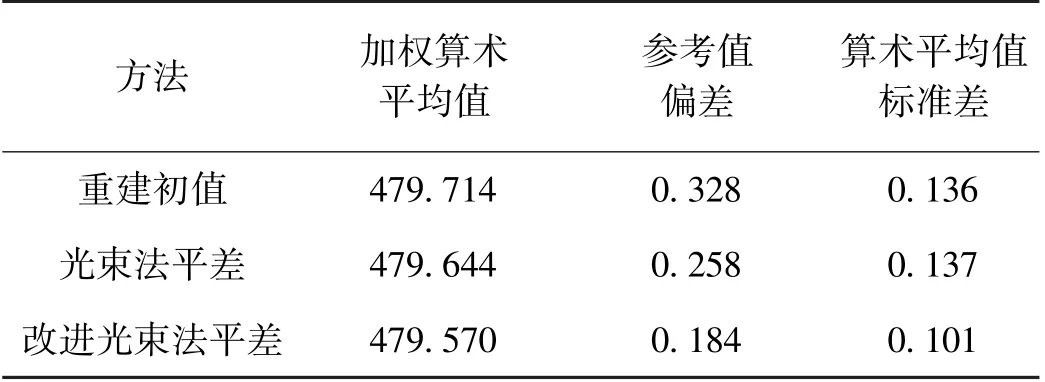
表6 d2数据处理结果 mm
表5中三种方法的参考值偏差均为负值,这是因为本系统利用棋盘格对相机进行标定,由于棋盘格相对于整个视场环境较小,标定过程中难以获取足够多的视觉信息,影响了相机畸变参数的标定。由于距离d1较长,整体的实验测量中,标志点三维坐标的求解受镜头径向畸变影响较大,从而导致距离d1的测量值整体上小于参考值。
综上所述,在对一维基准尺的长度测量实验中,对于长度d1,相较常规光束法平差,改进后光束法平差处理结果的参考值偏差减小了52.7%,算术平均值标准差减小了59.9%;对于长度d2,相较常规光束法平差,改进后光束法平差的参考值偏差减小了28.7%,算术平均值标准差减小了26.3%。由此可知,在两种长度的测量上,改进后光束法平差的处理精度相较常规光束法平差有显著提升。
4 结论
针对多目视觉测量系统,研究了多目视觉的三维重建原理和光束法平差原理,为了更好地表征本系统在三维空间中的定位误差,以及解决三维坐标值在迭代过程中修正不明显的问题,本文对传统光束法平差进行了改进,引入摄影比例尺建立新的误差方程并分步优化相机参数和三维坐标。实验结果表明:在一维基准尺的长度测量中,传统光束法平差测量结果与参考值偏差小于0.600 mm,标准差小于0.300 mm,改进后光束法平差测量结果与参考值偏差小于0.300 mm,标准差不大于0.110 mm,证明本文提出的方法有效地提升了多目视觉测量系统的测量精度,满足三维扫描测量机器人系统的应用需求。由于本文采用LM算法进行非线性优化,系统实验过程中求解每组数据的迭代次数一般在30~50次之间,迭代效率较低,未来可以在最优化算法方面展开进一步的研究,提升光束法平差处理数据的效率,推动三维测量技术提升。
